Quartile Deviation

We have seen that range is the simplest to understand and easiest to compute. But range as a measure of dispersion has certain limitations. The presence of even one extreme item (high or low) in a distribution can reduce the utility of range as a measure of dispersion. Since it is based on two extreme items (highest and lowest) it fails to take into account the scatter within the range. Hence we need a measure of dispersion to overcome these limitations of range. Such a measure of dispersion is called quartile deviation. In the previous chapter we studied quartiles. Quartiles are those values which divide the series into four equal parts. Hence we have three quartiles-Q₁, Q₂, and Q₃. Q₁ is the lower quartile wherein \( { \frac{{1}}{{4}}} \)^th of the total observations lie below it and \( { \frac{{3}}{{4}}} \)^th above it. Q₂ is same as median which divides the series into two equal parts. Q₃ is the upper quartile, \( { \frac{{3}}{{4}}} \)^th of the value falls below it and \( { \frac{{1}}{{4}}} \)^th above.

We have already studied the value of Q₁ and Q₃ for individual, discrete and continuous series, hence not repeated.

Upper and lower quartile ( Q₁ and Q₃ ) are used to calculate inter-quartile range.

$$ \mathbf {Inter-quartile\, range \,= Q_3\,-\,Q_1} $$ Half of inter-quartile range is called quartile deviation.

Quartile deviation (semi inter-quartile range) is defined as half the distance between the third and first quartiles.

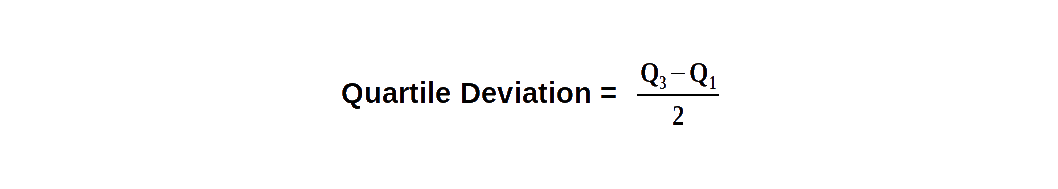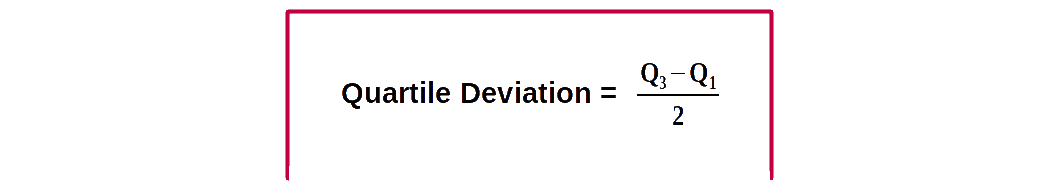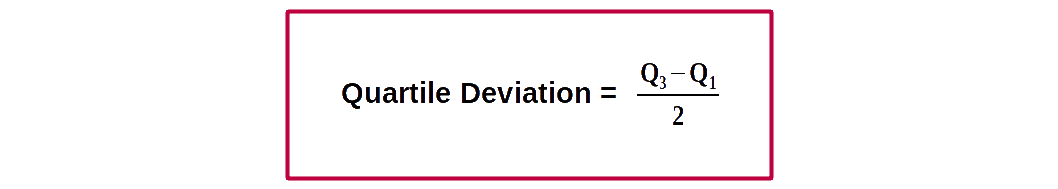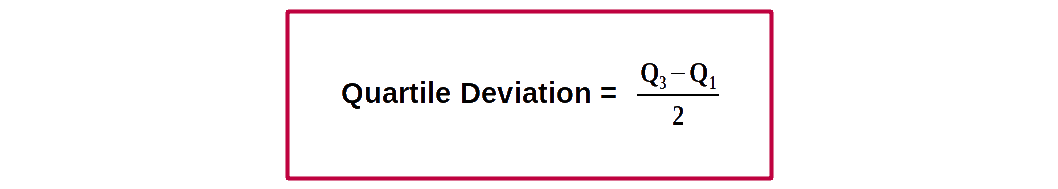
Quartile Deviation and inter quartile range are absolute measures of dispersion. The relative measure is coefficient of Quartile Deviation (Q.D)

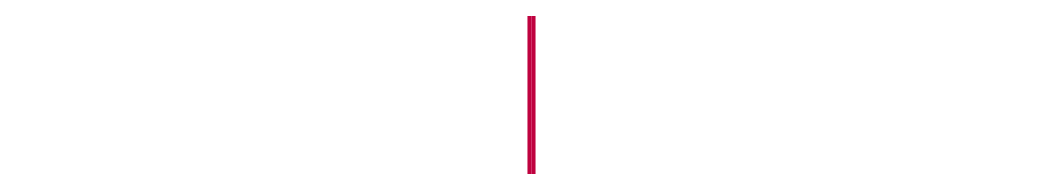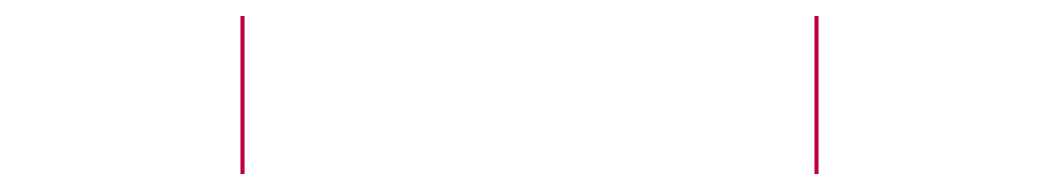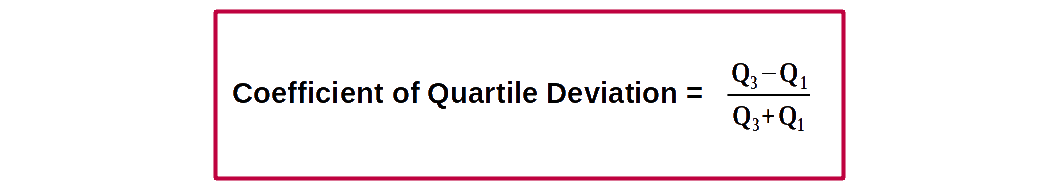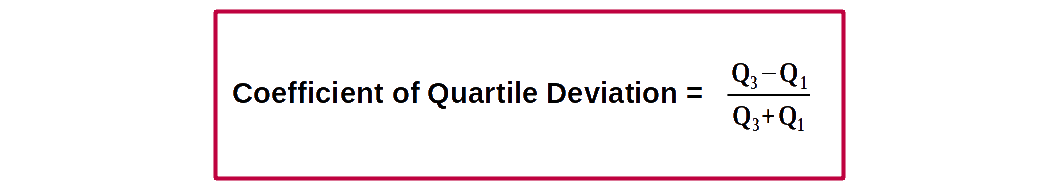
Individual Series

STEPS:-

Let us find the value of quartile deviation and its coefficient from the following data.

Table 6.6
Roll No.	Marks
1	20
2	28
3	40
4	12
5	30
6	15
7	50

We need to arrange Marks given in ascending order.

12, 15, 20, 28, 30, 40. 50

$$ Q_1 \,= \,Size \,of\,\Biggl[{{\frac{N + 1 }{4}}}\Biggl]^{th} item $$ $$ = \,Size \,of\,\Biggl[{{\frac{7 + 1 }{4}}}\Biggl]^{th} item $$ $$ = 2^{nd}\,item$$ Size of 2^nd item is 15. Thus Q₁ = 15

$$ Q_3 \,= \,Size \,of\,3\Biggl[{{\frac{N + 1 }{4}}}\Biggl]^{th} item $$ $$ Q_3 \,= \,Size \,of\,3\Biggl[{{\frac{7 + 1 }{4}}}\Biggl]^{th} item $$ $$ = Size\, of\, 6^{th}\,item$$ Size of 6^th item = 40; Q₃ = 40.

$$Q.D \,=\, {{{\frac{Q_3 - Q_1}{2}} }} $$ $$ = \,{{{\frac{40 - 15}{2}} }} $$ $$ = \,{{{\frac{25}{2}} }} $$ $$ = \, 12.5 $$ $$Coefficient \,of \,Q.D \,=\, {{{\frac{Q_3 - Q_1}{Q_3 + Q_1}} }} $$ $$=\, {{{\frac{40 - 15}{40 + 15}} }} $$ $$=\, {{{\frac{25}{55}} }} $$ $$ = \, 0.455 $$

Discrete Series

STEPS:-

Let us find the value of inter-quartile range, quartile deviation and its coefficient from the following data.

Table 6.7
Marks	No. of Students
10	4
20	7
30	15
40	8
50	7
60	2

Now we can create a table showing cumulative frequency (C.F) .

Table 6.8
Marks	No. of Students	C.F
10	4	4
20	7	11
30	15	26
40	8	34
50	7	41
60	2	43

$$ Q_1 \,= \,Size \,of\,\Biggl[{{\frac{N + 1 }{4}}}\Biggl]^{th} item $$ $$ = \,Size \,of\,\Biggl[{{\frac{43 + 1 }{4}}}\Biggl]^{th} item $$ $$ = 11^{th}\,item $$ Size of 11^th item = 20; Q₁ = 20.

$$ Q_3 \,= \,Size \,of\,3\Biggl[{{\frac{N + 1 }{4}}}\Biggl]^{th} item $$ $$ = \,Size \,of\,3\Biggl[{{\frac{43 + 1 }{4}}}\Biggl]^{th} item $$ $$ = \,Size \,of\Biggl[{{\frac{3 × 44 }{4}}}\Biggl]^{th} item $$ $$ = Size\, of\, 33^{rd}\,item$$ Size of 33^rd item = 40; Q₃ = 40.

$$ Inter-quartile \,range \,=\, Q_3\, - \,Q_1 $$ $$ =\, 40\, - \,20 $$ $$ =\,20 $$ $$ Q.D \,=\, {{{\frac{Q_3 - Q_1}{2}} }} $$ $$ = \,{{{\frac{40 - 20}{2}} }} $$ $$ = \,{{{\frac{20}{2}} }} $$ $$ = \, 10 $$ $$ Coefficient \,of \,Q.D \,=\, {{{\frac{Q_3 - Q_1}{Q_3 + Q_1}} }} $$ $$ =\, {{{\frac{40 - 20}{40 + 20}} }} $$ $$ =\, {{{\frac{20}{60}} }} $$ $$ = \, 0.333 $$

Continuous Series

STEPS:-

In the following table the figures relating to the wages of 60 workers in a company are given. Let us calculate the inter quartile range, quartile deviation and its coefficient.

Table 6.9
Wages (₹)	No. of Workers
20 - 25	2
25 - 30	10
30 - 35	25
35 - 40	16
40 - 45	7

Now we can create a table showing cumulative frequency (C.F) .

Table 6.10
Wages (₹)	No. of Workers	C.F
20 - 25	2	2
25 - 30	10	12
30 - 35	25	37
35 - 40	16	53
40 - 45	7	60
	N = 60

$$ Q_1\,=\,Size\,of\,{{{\frac{N}{4}} }}^{th} item $$ $$ =\,{{{\frac{60}{4}} }} $$ $$ =\,15^{th} item $$ Q₁ lies in the class 30 - 35

$$ Q_1 \,= \,{ L + \frac{\frac{N}{4} - {cf}}{f} × h} $$ L = 30;

\( {\frac{N}{4}} \) = 15;

CF = 12;

f = 25;

h = 5

$$ Q_1 \,= \,{ 30 + \frac{{15} - {12}}{25} × 5} $$ $$ =\, 30 \,+\,0.6 $$ $$ =\,30.6 $$ $$ Q_3\,=\,Size\,of\,{{{\frac{3N}{4}} }}^{th} item $$ $$ =\,{{{\frac{3 × 60}{4}} }} $$ $$ =\,{{{\frac{180}{4}} }} $$ $$ =\,45^{th} item $$ Q₃ lies in the class 35 - 40

$$ Q_3 \,= \,{ L + \frac{\frac{3N}{4} - {cf}}{f} × h} $$ L = 35;

\( {\frac{3N}{4}} \) = 45;

CF = 37;

f = 16;

h = 5

$$ Q_3 \,= \,{ 35 + \frac{{45} - {37}}{16} × 5} $$ $$ =\, 35 \,+\,2.5 $$ $$ =\, 37.5 $$ $$ Inter-quartile \,range \,=\, Q_3\, - \,Q_1 $$ $$ =\, 37.5\, - \,30.6 $$ $$ =\,6.9 $$ $$ Q.D \,=\, {{{\frac{Q_3 - Q_1}{2}} }} $$ $$ = \,{{{\frac{37.5 - 30.6}{2}} }} $$ $$ = \,{{{\frac{6.9}{2}} }} $$ $$ = \, 3.45 $$ $$ Coefficient \,of \,Q.D \,=\, {{{\frac{Q_3 - Q_1}{Q_3 + Q_1}} }} $$ $$ =\, {{{\frac{37.5 - 30.6}{37.5 + 30.6}} }} $$ $$ =\, {{{\frac{6.9}{68.1}} }} $$ $$ = \, 0.101 $$

MERITS OF QUARTILE DEVIATION

• It is easily computed and readily understood.
• It is not affected by extreme items.
• It can be computed even for an open end distribution.
• It is superior and more reliable than the range.

DEMERITS OF QUARTILE DEVIATION

• It is not based on all the items in a series.
• It is not based on all the observations.
• It is not capable of further algebraic treatment.
• It does not indicate variation of items from the average.
• Its value is very much affected by sampling fluctuations.