27 August
August 27, 2020 Note in English Questions and Answers

പഠന കുറിപ്പുകൾ.

ഒരു സ്ഥാപനത്തിന്റെ ഉല്പാദന ധർമം,ചെലവ് ധർമം എന്നിവയെക്കുറിച്ചാണ് കഴിഞ്ഞ അധ്യായത്തിൽ നമ്മൾ പഠിച്ചത്. സമ്പൂർണ കിടമത്സര കമ്പോളത്തിലെ ഒരു സ്ഥാപനത്തിന്റെ ഉല്പന്നത്തിന്റെ വില, ഉല്പാദനത്തിന്റെ അളവ് നിർണയം, സ്ഥാപനത്തിന്റെ സന്തുലിതാവസ്ഥ, പ്രദാനം, പ്രദാനത്തിന്റെ വില ഇലാസ്തികത തുടങ്ങിയവയാണ് നാം ഈ അധ്യായത്തിൽ പഠിക്കാൻ പോകുന്നത്.

കമ്പോളം (Market)

ഒരു സാധാരണ വ്യക്തിയെ സംബന്ധിച്ചിടത്തോളം കമ്പോളം എന്നു പറയുന്നത് സാധനങ്ങൾ വാങ്ങുകയും വിൽക്കുകയും ചെയ്യുന്ന ഒരു ഭൂപ്രദേശമാണ്. എന്നാൽ സാമ്പത്തിക ശാസ്ത്രത്തിൽ കൂടുതൽ വിശാലമായ അർത്ഥത്തിലാണ് ഈ പദം ഉപയോഗിക്കുന്നത്. സാധനങ്ങളും സേവനങ്ങളും വാങ്ങുന്നതിനും വില്ക്കുന്നതിനും ക്രേതാക്കളും (buyers) വിക്രേതാക്കളും (sellers) പരസ്പരം സമ്പർക്കത്തിൽ ഏർപ്പെടുന്ന സംവിധാനമാണ് കമ്പോളം.

കമ്പോള രൂപങ്ങൾ (Forms of Market)

കമ്പോളത്തെ താഴെ കൊടുത്തിരിക്കുന്ന വിധത്തിൽ തരംതിരിച്ചിരിക്കുന്നു.
  • 1. സമ്പൂർണ കിടമത്സരം
  • 2. അപൂർണ കിടമത്സരം
    • (a) കുത്തകാധിഷ്ഠിതമായ മത്സരം
    • (b) അാധീശത്വ വ്യാപാരം
  • 3. കുത്തക

സമ്പൂർണ കിടമത്സരം (Perfect Competition)

പ്രായോഗിക തലത്തിൽ അത്യപൂർവമായി കാണുന്ന ഒരു കമ്പോളമാണ് സമ്പൂർണ കിടമത്സരം അഥവാ പരിപൂർണ കിടമത്സരം. ദൈനംദിന ജീവിതത്തിൽ ഉപയോഗിക്കുന്നതിന് വിപരീത അർത്ഥത്തിലാണ് സമ്പൂർണ കിടമത്സരം എന്ന പദം സാമ്പത്തിക ശാസ്ത്രത്തിൽ ഉപയോഗിക്കുന്നത്. ഉല്പാദന സ്ഥാപനങ്ങൾ തമ്മിൽ മത്സരം ഇല്ലാത്ത ഒരു കമ്പോളമാണിത്. സ്ഥാപനങ്ങൾക്കിടയിൽ എതിരാളികൾ ഇല്ലാത്ത ഒരു കമ്പോള സിദ്ധാന്തമാണ് പൂർണ കിടമത്സരം എന്നതുകൊണ്ട് സൂചിപ്പിക്കുന്നത്.
ഏകജാതീയ (homogeneous) ഉല്പന്നങ്ങൾ കൈകാര്യം ചെയ്യുന്ന ധാരാളം ക്രേതാക്കളും വിക്രേതാക്കളും ഉള്ള ഒരു കമ്പോള സംവിധാനത്തെയാണ് സമ്പൂർണ കിടമത്സര കമ്പോളം എന്നു പറയുന്നത്. സമ്പൂർണ കിടമത്സര കമ്പോളത്തിന് താഴെ പറയുന്ന സവിശേഷതകൾ ഉണ്ടായിരിക്കും:
  • 1. വളരെയധികം ക്രേതാക്കളും വിക്രേതാക്കളും ഉണ്ടായിരിക്കും.
  • 2. എല്ലാ ഉല്പാദക സ്ഥാപനങ്ങളും ഉല്പാദിപ്പിക്കുന്ന സാധനം ഏകജാതീയമായിരിക്കും.
  • 3. സ്ഥാപനങ്ങൾക്ക് കമ്പോളത്തിലേക്ക് പ്രവേശിക്കാനും ഉല്പാദനം നിർത്തി പുറത്തുപോകാനും പൂർർണസ്വാതന്ത്ര്യം ഉണ്ടായിരിക്കും.
  • 4. കമ്പോള സ്ഥിതിയെക്കുറിച്ച് പൂർണ അറിവ് ഉണ്ടായിരിക്കും.
  • 5. ഉല്പാദനഘടകങ്ങൾക്കും സാധനങ്ങൾക്കും പൂർണ ചലനസ്വാതന്ത്ര്യമുണ്ടായിരിക്കും.
  • 6. ഗതാഗതച്ചെലവ് ഉണ്ടായിരിക്കില്ല.
  • 7. സാധനങ്ങൾക്ക് സമാന വിലയായിരിക്കും.
  • 8. സാധനങ്ങൾക്ക് പൂർണ ഇലാസ്തിക ചോദനമായിരിക്കും.
  • 9. ഗവൺമെന്റ് നിയന്ത്രണം ഇല്ല.
  • 10. വില്പന ചെലവില്ല.

സമ്പൂർണ കിടമത്സര കമ്പോളത്തിലെ രണ്ട് നിർണായക സവിശേഷതകളാണ് (1) ഏകജാതീയ ഉല്പന്നങ്ങൾ (2) വില സ്വീകരിക്കുന്ന ഉല്പാദകരും ഉപഭോക്താക്കളും.
സമ്പൂർണ കിടമത്സര കമ്പോളത്തിലെ ഒരു നിർണായക സവിശേഷതയാണ് ഈ കമ്പോളത്തിലുള്ള ഉല്പാദകർ ഉല്പാദിപ്പിക്കുന്ന ഉല്പന്നങ്ങൾ എല്ലാം ഒരേപോലെയുള്ള ഉല്പന്നങ്ങളാണ് എന്നത്. ഉല്പന്നങ്ങൾ തമ്മിൽ യാതൊരു വ്യത്യാസവുമില്ല. അവയുടെ നിറം, മണം, ഗുണം, വലിപ്പം എന്നിവയെല്ലാം ഒരേ പോലെയായിരിക്കും. രണ്ടാമത്തെ സവിശേഷതയനുസരിച്ച് സമ്പൂർണ കിടമത്സര കമ്പോളത്തിലെ ഓരോ ക്രേതാവും (വാങ്ങുന്നവൻ) വിക്രേതാവും (വില്ക്കുന്നവൻ) “വില സ്വീകരിക്കുന്നവൻ (Price-taker)” ആയിരിക്കും. അതായത്, കമ്പോളത്തിൽ നിലവിലുള്ള വില ക്രേതാക്കളും വിക്രേതാക്കളും സ്വീകരിക്കേണ്ടി വരുന്നു. ഉല്പാദകനോ ഉപഭോക്താവിനോ വിലയെ സ്വാധീനിക്കാൻ കഴിയില്ല. വില സ്വീകരിക്കുന്നവൻ എന്നതുകൊണ്ട് രണ്ട് കാര്യങ്ങൾ സൂചിപ്പിക്കുന്നു.
ഏതെങ്കിലും ഒരു ഉല്പാദകൻ കമ്പോളവിലയേക്കാൾ ഉയർന്ന വില നിശ്ചയിച്ചാൽ ആ ഉല്പാദകന് ഉപഭോക്താക്കളെ നഷ്ടമാകും. അയാൾ ഉല്പാദിപ്പിക്കുന്ന സാധനത്തിന് ചോദനം ഇല്ലാതെയാവുകയും ഉല്പാദനം നിർത്തിപ്പോകേണ്ടി വരികയും ചെയ്യും. ഉല്പാദകന് “സാധാരണ ലാഭം (Normal Profit)” മാത്രം ലഭിക്കുന്നതു കൊണ്ട് കമ്പോളവിലയേക്കാൾ കുറഞ്ഞ വിലയ്ക്ക് സാധനം വില്ക്കാൻ അദ്ദേഹം തയ്യാറാവുകയില്ല.

ഒരു ഉപഭോക്താവിനെ സംബന്ധിച്ചിടത്തോളം ഏറ്റവും കുറഞ്ഞ വിലയ്ക്ക് സാധനങ്ങൾ വാങ്ങാൻ അയാൾ ആഗ്രഹിക്കുന്നു. കമ്പോളവിലയേക്കാൾ കുറഞ്ഞ വിലയ്ക്ക് ഉപഭോക്താവിന് സാധനം ലഭ്യമാകുകയില്ല. എന്തുകൊണ്ടെന്നാൽ കമ്പോളവിലയേക്കാൾ കുറഞ്ഞ വിലയ്ക്ക് സാധനം വില്ക്കാൻ ഉല്പാദകൻ തയ്യാറാകുകയില്ല. ഉപഭോക്താവിന് കമ്പോള വിലയ്ക്ക് എത്ര അളവ് സാധനവും ലഭ്യമാകും.
ചുരുക്കത്തിൽ സമ്പൂർണ കിടമത്സര കമ്പോളത്തിൽ സാധനത്തിന്റെ വില എപ്പോഴും കമ്പോളവിലയ്ക്ക് തുല്യമായിരിക്കും. ഈ വിലയ്ക്ക് ഒരു സാധനത്തിന്റെ എത്ര അളവ് വേണമെങ്കിലും വില്ക്കുവാനും വാങ്ങുവാനും കഴിയും. അതുകൊണ്ട്, ഉല്പാദകൻ വില്ക്കുന്ന ഉല്പന്നത്തിന്റെ ഓരോ യൂണിറ്റിന്റെയും വില സ്ഥിരമായിരിക്കും. കമ്പോളവിലയ്ക്ക് ഉല്പാദകന് ഏതളവ് സാധനം വില്ക്കുവാനും ഉപഭോക്താവിന് ഏതളവ് സാധനം വാങ്ങുവാനും കഴിയുന്നതു കൊണ്ട് സമ്പൂർണ കിടമത്സര കമ്പോളത്തിലെ ഓരോ ഉല്പാദകനെയും ഓരോ ഉപഭോക്താക്കളെയും വില സ്വീകരിക്കുന്നവൻ എന്നു വിളിക്കുന്നു.

വരുമാനം (Revenue)

ഒരു ഉല്പാദകൻ ഉല്പാദിപ്പിച്ച ഉല്പന്നം കമ്പോളത്തിൽ വില്ക്കുമ്പോൾ ലഭിക്കുന്ന വരവിനെ വരുമാനം അഥവാ വിറ്റുവരവ് എന്നു പറയുന്നു. ഒരു ഉല്പാദക യൂണിറ്റ് ഉല്പാദിപ്പിക്കുന്ന സാധനങ്ങൾ വില്ക്കുമ്പോൾ കിട്ടുന്ന ആകെ തുകയെ മൊത്തം വരുമാനം (Total Revenue - TR) എന്നു പറയുന്നു. കമ്പോളവിലയെ (p) ഉല്പന്നത്തിന്റെ അളവുകൊണ്ട് (q) ഗുണിച്ചാണ് മൊത്തം വരുമാനം കാണുന്നത്. അതായത്, TR = p × q
Eg 4.1: സമ്പൂർണ കിടമത്സര കമ്പോളത്തിൽ ഉല്പന്നത്തിന്റെ വില സ്ഥിരമാണ്. ഉദാഹരണമായി, പട്ടിക 4.1 ൽ ഉല്പന്നത്തിന്റെ വില 10 യും ഉല്പന്നത്തിന്റെ വിവിധ അളവും കൊടുത്തിരിക്കുന്നു. വിലയെ ഉല്പന്നത്തിന്റെ അളവുകൊണ്ട് ഗുണിച്ച് മൊത്തം വരുമാനം കണക്കാക്കിയിരിക്കുന്നത് നോക്കുക.

Table 4.1 മൊത്തം വരുമാനം
വില (P) ഉല്പന്നത്തിന്റെ അളവ് (Q) മൊത്തം വരുമാനം = P × Q
10 0 0
10 1 10
10 2 20
10 3 30
10 4 40
10 5 50
10 6 60

ഒരു സ്ഥാപനത്തിന്റെ മൊത്തം വരുമാനവും ഉല്പന്നവും തമ്മിലുള്ള ബന്ധമാണ് TR വക്രം സൂചിപ്പിക്കുന്നത്. ഗ്രാഫ് 4.1 ൽ y-അക്ഷത്തിൽ TR ഉം x-അക്ഷത്തിൽ ഉല്പന്നത്തിന്റെ അളവും രേഖപ്പെടുത്തിയിരിക്കുന്നു. TR എന്നതാണ് ഒരു സ്ഥാപനത്തിന്റെ മൊത്തം വരുമാന വക്രം.

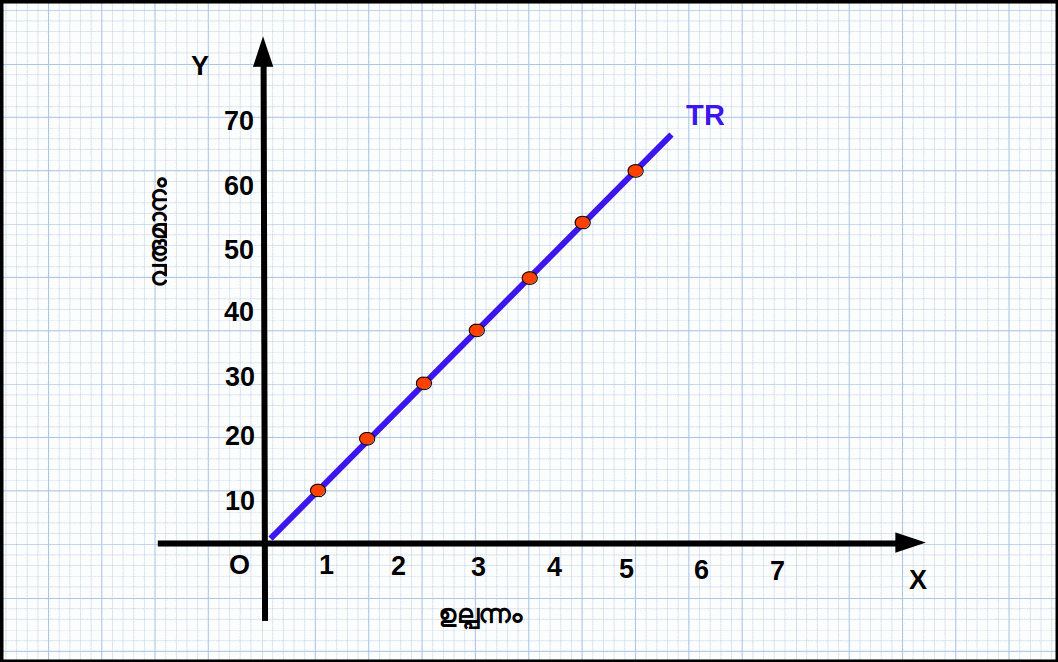
Total-Revenue-Curve

Diagram 4.1 മൊത്തം വരുമാനവക്രം

ഈ ഗ്രാഫിൽ താഴെ പറയുന്ന മൂന്നു കാര്യങ്ങൾ നമുക്ക് കാണാൻ സാധിക്കും.
  • 1. പൂജ്യം ഉല്പന്നത്തിൽ മൊത്തം വരുമാനവും പൂജ്യമായിരിക്കും. അതുകൊണ്ട് TR വക്രം O എന്ന ബിന്ദുവിൽ കൂടി കടന്നുപോകുന്നു.
  • 2. ഉല്പന്നത്തിന്റെ അളവ് വർധിക്കുന്നതിനനു സരിച്ച് TR ഉയരുന്നു. കൂടാതെ TR വക്രം മുകളിലേക്ക് ഉയരുന്ന ഒരു നേർരേഖയാണ്.
  • 3. TR വക്രത്തിന്റെ ചരിവ് വിലയ്ക്ക് തുല്യമാണ്. ഉല്പന്നം 1 യൂണിറ്റ് മാറുമ്പോൾ മൊത്തം വരുമാനത്തിലുള്ള മാറ്റം 10 ആണ്.

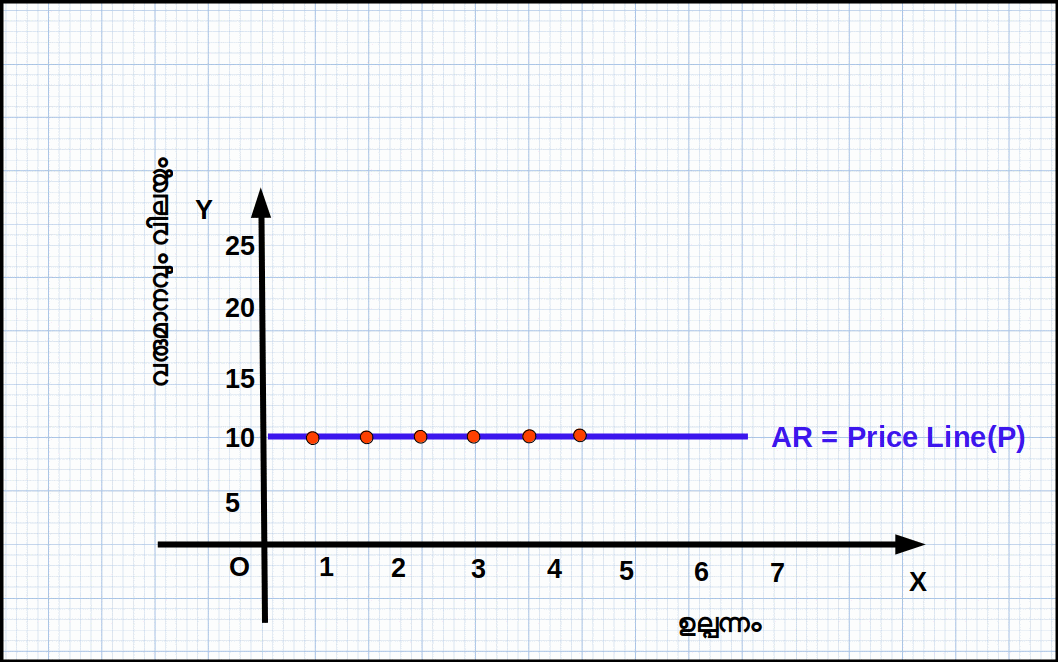
വില രേഖ (Price Line)

വിലയും ഉല്പന്നവും തമ്മിലുള്ള ബന്ധത്തെ വിലരേഖ സൂചിപ്പിക്കുന്നു. സമ്പൂർണ കിടമത്സര കമ്പോളത്തിൽ ഒരു സ്ഥാപനത്തിന്റെ ഉല്പന്നം വിലയെ ആശ്രയിച്ചല്ല നിലനിൽക്കുന്നത്. ഇത് അർത്ഥമാക്കുന്നത് നിശ്ചിത വിലയ്ക്ക് എത്ര യൂണിറ്റ് ഉല്പന്നം വേണമെങ്കിലും വില്ക്കാൻ സാധ്യമാണെന്നാണ്. പട്ടിക 4.1 ൽ ഉല്പന്നത്തിന്റെ വില 10 ആണ്. ഉല്പന്നത്തിന്റെ അളവ് വർധിക്കുന്നതിനനുസരിച്ച് വിലയിൽ മാറ്റമില്ല. വിലയും ഉല്പന്നവും തമ്മിലുള്ള ബന്ധം കാണിക്കുന്ന രേഖയെയാണ് വില രേഖ എന്നു പറയുന്നത്.
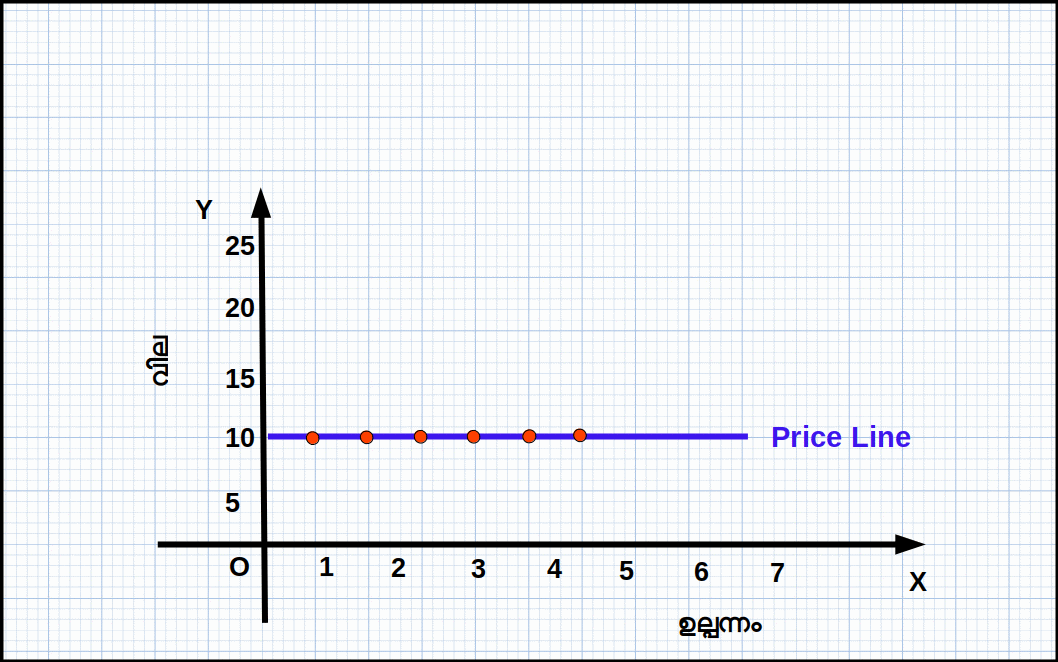
Eg 4.2; വില y-അക്ഷത്തിലും ഉല്പന്നം x-അക്ഷത്തിലും അടയാളപ്പെടുത്തി വില ഉല്പന്ന സംയോഗങ്ങൾ ചേർത്ത് വരച്ചാൽ ഗ്രാഫ് 4.2 ൽ കാണുന്നതുപോലെ ഒരു ഹൊറിസോണ്ടൽ രേഖ ലഭിക്കുന്നു; ഇതാണ് വിലരേഖ. വിലരേഖ X-അക്ഷത്തിന് സമാന്തരമാണ്.

Price-Line

Diagram 4.2 വില രേഖ

ശരാശരി വരുമാനം (Average Revenue - AR)

വിറ്റ ഉല്പന്നത്തിന്റെ ഓരോ യൂണിറ്റിൽ നിന്നുമുള്ള വരുമാനമാണ് ശരാശരി വരുമാനം. മൊത്തം വരുമാനത്തെ വിറ്റ ഉല്പന്നത്തിന്റെ അളവുകൊണ്ട് ഹരിച്ചാണ് ശരാശരി വരുമാനം കാണുന്നത്. ഗണിത രൂപത്തിൽ

\( \mathbf{AR \,=\, {\frac{TR}{q}} } \) = \( \mathbf{{\frac{pq}{q}} } \) = p

AR വിലയ്ക്ക് തുല്യമാണ്. അതുകൊണ്ട്, വിലരേഖയും AR വക്രവും ഒന്നുതന്നെയാണ്. ഈ രേഖയാണ് സമ്പൂർണ കിടമത്സര കമ്പോളത്തിലെ ചോദന വക്രം.
Eg 4.3: പട്ടിക 4.2 ൽ TR ഉം AR ഉം കൊടുത്തിരിക്കുന്നു. സാധനത്തിന്റെ ഒരു യൂണിറ്റിന്റെ വില 10 യാണ്.

Table 4.2 ശരാശരി വരുമാനം
വില (P) ഉല്പന്നം (Q) മൊത്തം വരുമാനം (TR = P×Q) ശരാശരി വരുമാനം (\(\mathbf{AR=\frac{TR}{Q}}\))
10 0 0 0
10 1 10 10÷1=10
10 2 20 20÷2=10
10 3 30 30÷3=10
10 4 40 40÷4=10
10 5 50 50÷5=10
10 6 60 60÷6=10

പട്ടികയിൽ AR ഉം വിലയും തുല്യമാണ്.
അതായത്, AR = P = 10. അതുകൊണ്ട് AR വക്രം വിലരേഖ തന്നെയാണ്.

AR-and-Price-Line

Diagram 4.3 വില രേഖയും ശരാശരി വക്രവും

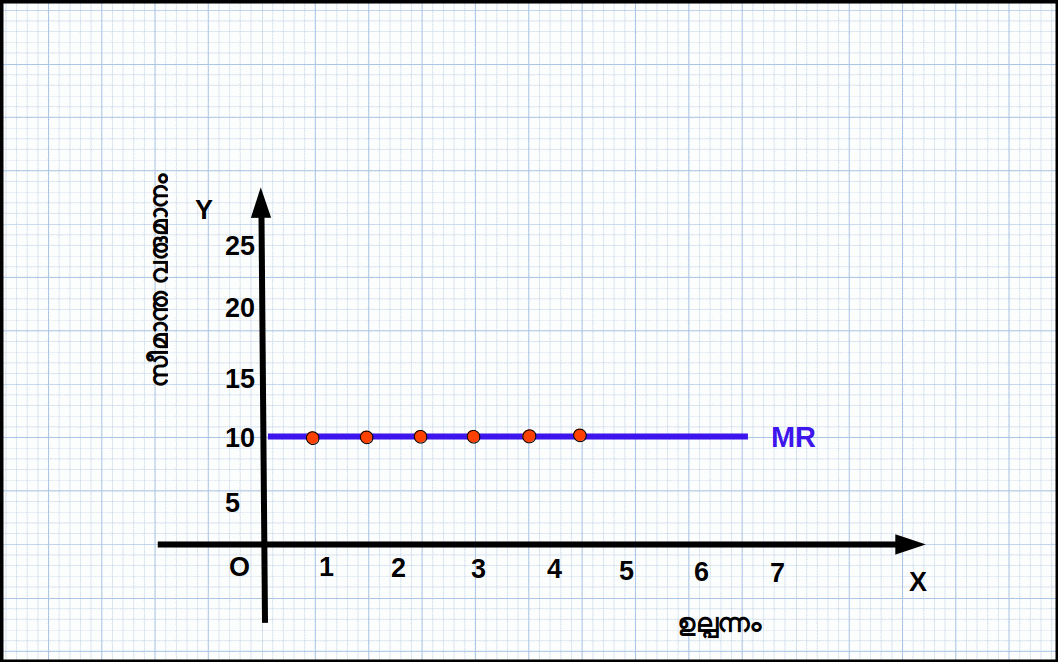
സീമാന്ത വരുമാനം (Marginal Revenue - MR)

ഉല്പന്നത്തിന്റെ ഒരു അധിക യൂണിറ്റ് വിൽക്കുന്നതു വഴി ലഭിക്കുന്ന അധിക വരുമാനമാണ് സീമാന്ത വരുമാനം. മൊത്തം വരുമാനത്തിലുള്ള മാറ്റമാണ് ഇത്. മൊത്തം വരുമാനത്തിന്റെ മാറ്റത്തിന്റെ നിരക്കാണ് സീമാന്ത വരുമാനം. ഒരു ഉല്പാദക യൂണിറ്റിന്റെ ഉല്പന്നത്തിന്റെ അളവ് q° ൽനിന്ന് (q° + 1) ആയി വർധിക്കുന്നുവെന്ന് കരുതുക. അപ്പോൾ,
MR = [(q° + 1) ഉല്പന്നത്തിൽ നിന്നുള്ള TR] - [q° ഉല്പന്നത്തിൽ നിന്നുള്ള TR]
വില p ആണെങ്കിൽ,

MR = [p(q° + 1)] - (pq°)
= pq° + p - pq° = p

വില സ്വീകരിക്കുന്ന ഒരു കമ്പോളത്തിൽ സീമാന്ത വരുമാനം വിലയ്ക്ക് തുല്യമാണ് (MR = P).

Marginal Revenue

(\(\mathbf{MR=\frac{ΔTR}{Δq}}\))

MRn = TRn - TRn - 1

MRn = n യൂണിറ്റിലുള്ള MR

TRn = n യൂണിറ്റ് വില്പനയിൽനിന്നുള്ള TR

TRn - 1 = n - 1 യൂണിറ്റ് വില്പനയിൽനിന്നുള്ള TR

Eg. 4.4: പട്ടിക 4.3 നിരീക്ഷിക്കുക. ഉല്പന്നത്തിന്റെ അളവ് 0 യൂണിറ്റിൽ നിന്ന് 1 യൂണിറ്റായി വർധിച്ചപ്പോൾ TR പൂജ്യത്തിൽ നിന്ന് 10 രൂപയായി വർധിക്കുന്നു. അപ്പോൾ, MR1 = TR1 - TR0 = 10 - 0 = 10 രൂപയാണ്. അതുപോലെ, ഒന്നാമത്തെ യൂണിറ്റ് വിറ്റപ്പോൾ TR 10 രൂപയാണ്. രണ്ട് യൂണിറ്റ് വിറ്റപ്പോൾ TR 20 രൂപയാണ്. അപ്പോൾ, MR2, = TR2, - TR1 = 20 – 10 = 10 ആണ്. ഇപ്രകാരം MR കാണാവുന്നതാണ്.
Table 4.3 മൊത്തം വരുമാനവും സീമാന്ത വരുമാനവും
ഉല്പന്നം (Q) മൊത്തം വരുമാനം (TR) സീമാന്ത വരുമാനം (\(\mathbf{MR = \frac{ΔTR}{ΔQ}}\))
0 0 -
1 10 10 ÷ 1 = 10
2 20 10 ÷ 1 = 10
3 30 10 ÷ 1 = 10
4 40 10 ÷ 1 = 10
5 50 10 ÷ 1 = 10
6 60 10 ÷ 1 = 10

പട്ടിക 4.3 ന്റെ അടിസ്ഥാനത്തിൽ ഗ്രാഫ് 4.4 ൽ സീമാന്ത വരുമാന വക്രം വരച്ചിരിക്കുന്നു. MR വക്രം X-അക്ഷത്തിന് സമാന്തരമാണ്.

Marginal-Revenue-Curve

Diagram 4.4 സീമാന്ത വരുമാന വക്രം

Problem 4.1: പട്ടികയനുസരിച്ച് താഴെ കൊടുത്തിരിക്കുന്ന ചോദ്യങ്ങൾക്ക് ഉത്തരം എഴുതുക.

Table 4.4
വില ഉല്പന്നം
2 0
2 1
2 2
2 3
2 4
2 5

  • 1. TR, AR, MR എന്നിവ കാണുക.
  • 2. TR, AR, MR എന്നിവ ഒരു ഗ്രാഫിൽ വരയ്ക്കുക.
  • 3. ഓരോ വക്രത്തിന്റെയും സവിശേഷതകൾ വിവരിക്കുക.

  1. Table 4.5
    P q TR=P × q \(\mathbf{AR=\frac{TR}{q}}\) \(\mathbf{MR=\frac{ΔTR}{Δq}}\)
    2 0 0 - -
    2 1 2 2 2
    2 2 4 2 2
    2 3 6 2 2
    2 4 8 2 2
    2 5 10 2 2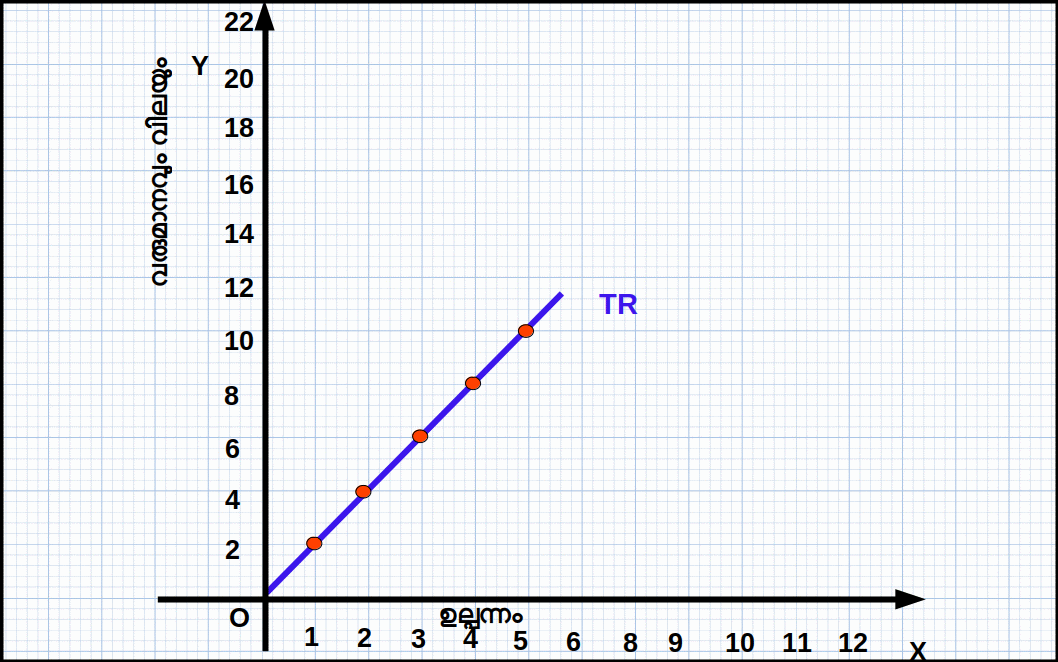

  2. AR-and-Price-Line

    Diagram 4.5

  3. TR വക്രം മുകളിലേക്ക് ഉയരുന്ന ഒരു നേർരേഖയാണ്. TR പൂജ്യത്തിൽനിന്ന് തുടങ്ങി ഉല്പന്നം വർധിക്കുന്നതിന് ആനുപാതികമായി വർധിക്കുന്നു. TR രേഖയുടെ ചരിവ് \(\mathbf{MR=\frac{ΔTR}{Δq}}\) = 2 ആണ്. വിലരേഖയ്ക്ക് തുല്യമാണ് AR, MR രേഖകൾ. ഇവ പരസ്പരം ചേർന്നിരിക്കുന്നു. ഉല്പന്നത്തിന്റെ അളവ് മാറുന്നതിനനുസരിച്ച് ഇവയിൽ മാറ്റം വരുന്നില്ല. ഇവ x-അക്ഷത്തിന് സമാന്തരമാണ്. സമ്പൂർണ കിടമത്സരത്തിൽ P = AR = MR വക്രമാണ് ചോദന വക്രവും.

ലാഭം പരമാവധിയാക്കൽ (Profit Maximisation)

ഓരോ ഉല്പാദകനും സാധനങ്ങളോ സേവന ങ്ങളോ ഉല്പാദിപ്പിക്കുകയും അവ കമ്പോളത്തിൽ വിറ്റഴിക്കുകയും ചെയ്യുന്നു. എല്ലാ ഉല്പാദക യൂണിറ്റി ന്റെയും പ്രധാന ലക്ഷ്യം തന്റെ ലാഭം പരമാവധിയാ ക്കുക എന്നതാണ്. ഉല്പന്നങ്ങൾ കമ്പോളത്തിൽ വിറ്റ് ഉല്പാദകന്റെ ലാഭം പരമാവധിയിൽ എത്തുന്ന അവസ്ഥയെ സന്തുലിതാവസ്ഥ (equilibrium) എന്നു പറയുന്നു. അതായത്, ഉല്പാദകന് ഉല്പന്നത്തിന്റെ അളവ് വർധിപ്പിക്കാനോ കുറയ്ക്കാനോ താല്പര്യമില്ലാത്ത സ്ഥിതിയാണ് സന്തുലിതാവസ്ഥ. ഒരു ഉല്പാദക യൂണിറ്റിന്റെ TR ഉം TC യും തമ്മിലുള്ള വ്യത്യാസമാണ് ലാഭം ( π - പൈ). അതായത്,

π = TR - TC

അപ്പോൾ, ഒരു സ്ഥാപനം സന്തുലിതാവസ്ഥയിൽ എത്തുന്നത് TR ഉം TC യും തമ്മിലുള്ള വ്യത്യാസം ഏറ്റവും കൂടിയിരിക്കുമ്പോഴാണ്. TR ഉം TC യും തമ്മിലുള്ള വ്യത്യാസം ഏറ്റവും കൂടിയിരിക്കുന്നത് താഴെ പറയുന്ന മൂന്ന് വ്യവസ്ഥകൾ പാലിക്കുമ്പോഴാണ്. അതായത്, ഒരു സ്ഥാപനം സന്തുലിതാവസ്ഥ പ്രാപിക്കണമെങ്കിൽ മൂന്ന് വ്യവസ്ഥകൾ പാലിക്കണം:

  • 1. MC യും MR ഉം തുല്യമാകണം (MR=MC).
  • 2. സീമാന്ത ചെലവ് കുറയാതെയിരിക്കണം. മറ്റൊരു വിധത്തിൽ പറഞ്ഞാൽ MC വക്രം MR വക്രത്തെ താഴെനിന്ന് ഖണ്ഡിക്കണം.
  • 3. മൂന്നാമത്തെ വ്യവസ്ഥ:

    • (a) ഹ്രസ്വകാലഘട്ട ത്തിൽ വില ശരാശരി വിഭേദക ചെലവിന് തുല്യമോ അതിനേക്കാൾ കൂടുതലോ ആയിരിക്കണം. P ≥ AVC.
    • (b) ദീർഘകാലയളവിൽ വില ശരാശരി ചെലവിന് തുല്യമോ അതിനേക്കാൾ കൂടുതലോ ആയിരിക്കണം. P ≥ AC.
ഈ മൂന്ന് വ്യവസ്ഥകൾ വിശദമായി നമുക്ക് പരിശോധിക്കാം.
വ്യവസ്ഥ 1: വിലയും സീമാന്ത ചെലവും തുല്യമായിരിക്കണം എന്നതാണ് സമ്പൂർണ കിടമത്സര കമ്പോളത്തിലെ സന്തുലിതാവസ്ഥയുടെ ഒന്നാമത്തെ വ്യവസ്ഥ. വിലയും സീമാന്ത ചെലവും തുല്യമല്ലാതെ വരുമ്പോൾ രണ്ട് സ്ഥിതി ഉണ്ടാകുന്നു. (1) വില സീമാന്ത ചെലവിനേക്കാൾ കൂടിയിരിക്കുക (P > MC). (2) സീമാന്ത ചെലവ് വിലയേക്കാൾ കൂടിയിരിക്കുക (MC > P). ഈ രണ്ട് സ്ഥിതിയിലും ലാഭം പരമാവധിയിലാകുകയില്ല. ഈ രണ്ട് സ്ഥിതിയും നമുക്ക് ഒരു ഡയഗ്രത്തിന്റെ സഹായത്തോടെ വിശദമാക്കാം. സ്ഥിതി 1 സീമാന്ത ചെലവിനേക്കാൾ വില കൂടി യിരിക്കുന്നത് പരിഗണിക്കില്ല. ഡയഗ്രം 4.6 ൽ X-അക്ഷത്തിൽ ഉല്പന്നത്തിന്റെ അളവും y-അക്ഷത്തിൽ വിലയും സീമാന്ത ചെലവും രേഖപ്പെടുത്തിയിരിക്കുന്നു. P = MR = AR എന്നത് വിലരേഖയും MC എന്നത് സീമാന്ത ചെലവും വക്രവുമാണ്. MC വക്രം ഉല്പന്നത്തിന്റെ അളവ് വർധിക്കുന്നതിനനുസരിച്ച് ആദ്യം കുറയുകയും പിന്നീട് വർധിക്കുകയും ചെയ്യുന്നു.

MR-MC

Diagram 4.6

ഡയഗ്രം 4.6ൽ Q1 നും Q0 യ്ക്കും ഇടയിലുള്ള ഏതൊരു ഉല്പന്നതലത്തിലും MC യെക്കാൾ കൂടുതലാണ് വില. ഉദാഹരണമായി, ഉല്പന്നത്തിന്റെ അളവ് Q2 ൽ നിന്ന് Q3 ആയി വർധിപ്പിച്ചാൽ TR ലെ വർധനവ് Q2ABQ3 ഭാഗമാണ്. അപ്പോൾ TC ലെ വർധനവ് Q2DCQ3 ഭാഗമാണ്. മൊത്തം ലാഭത്തിലുള്ള വർധനവ് ABCD ഭാഗമാണ്. അതുകൊണ്ട് Q2 അളവ് ഉല്പന്നത്തിൽനിന്ന് ലഭിക്കുന്നതിനേക്കാൾ കൂടുതൽ ലാഭം Q3 അളവിലുള്ള ഉല്പന്നത്തിന് ലഭിക്കുന്നു. ഇനിയും ഉല്പന്നത്തിന്റെ അളവ് Q3 ൽനിന്ന് Q2 ആയി വർധിപ്പിച്ചാൽ ലാഭത്തിലുള്ള വർധനവ് BCE അധികം ലഭിക്കുന്നു. ആയതിനാൽ Q1 മുതൽ QQ2 വരെ ഉല്പന്നത്തിന്റെ അളവ് വർധിക്കുന്നതിനനുസരിച്ച് ലാഭവും വർധിക്കുന്നു. ലാഭം ഏറ്റവും കൂടുതൽ ലഭിക്കുന്ന ഉല്പന്നത്തിന്റെ അളവ് QQ0 ആണ്. Q0 ഉല്പന്ന തലത്തിൽ E എന്ന ബിന്ദുവിൽ വിലയും MC യും തുല്യമാണ് (P = MC).

സ്ഥിതി 2: സീമാന്ത ചെലവിനേക്കാൾ വില കുറഞ്ഞിരിക്കുന്നത് പരിഗണിക്കില്ല. ഉല്പന്നത്തിന്റെ അളവ് Q2 നു മുമ്പും Q0 നു ശേഷവും MC യെക്കാൾ കുറവാണ് വില. ഈ ഉല്പന്ന തലങ്ങളിൽ ലാഭം പരമാവധിയായിരിക്കുകയില്ല. അതുകൊണ്ട് ഈ സ്ഥിതി തള്ളിക്കളയുന്നു. സ്ഥാപനം ഉല്പന്നത്തിന്റെ അളവ് Q5 ൽ നിന്ന് Q4 ആയി കുറച്ചപ്പോൾ TR ലെ കുറവ് Q4Q5HI ഭാഗമാണ്. അപ്പോൾ TC യിലെ കുറവ് Q4Q5GF ഭാഗമാണ്. Q5 അധിക യൂണിറ്റ് ഉല്പാദിപ്പിക്കുന്നതു മൂലമുണ്ടാകുന്ന അധിക വരുമാനത്തേക്കാൾ കൂടുതലാണ് അധിക ചെലവ്. അതുകൊണ്ട്, Q5 ലെക്കാൾ ലാഭം Q4 ഉല്പന്ന തലത്തിലാണ്. അതിലും കൂടുതൽ ലാഭം Q0 യിൽ ലഭി ക്കുന്നു. Q0യ്ക്കു ശേഷം MC വിലയേക്കാൾ കൂടിയിരിക്കുന്നതുകൊണ്ട് ഉല്പന്നത്തിന്റെ അളവ് കുറച്ചുകൊണ്ട് സ്ഥാപനത്തിന് ലാഭം പരമാവധിയാക്കാൻ കഴിയും.
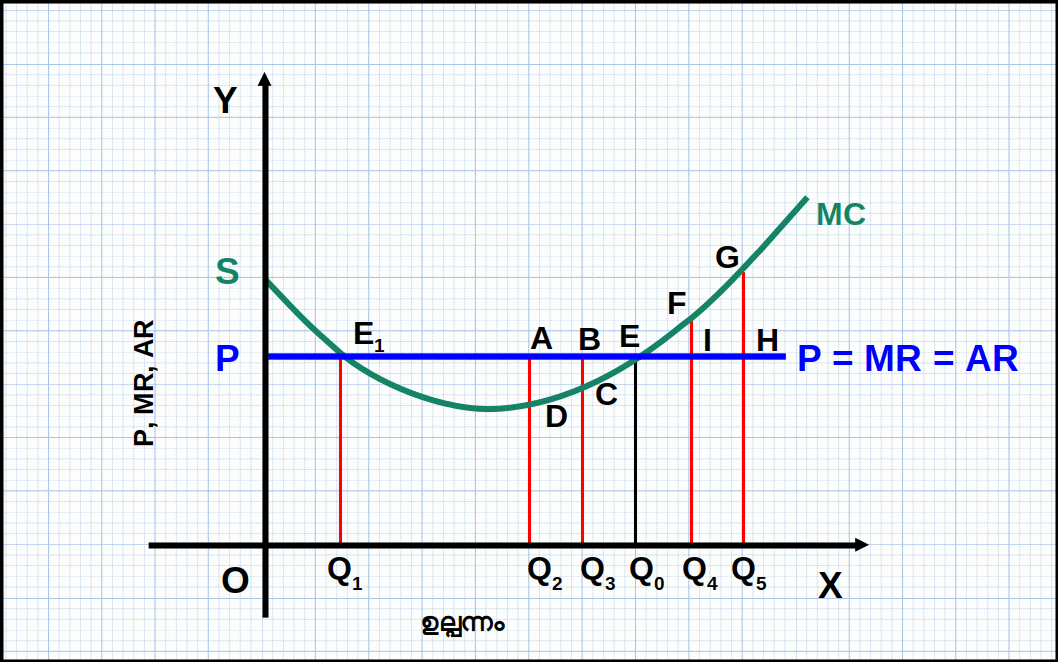
Q1 ന് മുമ്പുള്ള ഉല്പന്ന തലത്തിൽ MC വിലയേക്കാൾ കൂടിയിരിക്കുന്നതുകൊണ്ട് സ്ഥാപനത്തിന് നഷ്ടമാണ്. ഈ സാഹചര്യത്തിൽ ഉല്പന്നത്തിന്റെ അളവ് വർധിപ്പിച്ചുകൊണ്ട് സ്ഥാപനത്തിന് ലാഭം പരമാവധിയാക്കാൻ കഴിയും. E1 എന്ന ബിന്ദുവിൽ സീമാന്ത ചെലവും വിലയും തുല്യമാണ്. പക്ഷേ സ്ഥാപനത്തിന് നഷ്ടമാണ്.
വ്യവസ്ഥ 2: സന്തുലിത ഉല്പന്നത്തിൽ സീമാന്ത ചെലവ് കുറയാതെയിരിക്കണം എന്നതാണ് സമ്പൂർണ കിടമത്സര കമ്പോളത്തിന്റെ രണ്ടാമത്തെ വ്യവസ്ഥ. മറ്റൊരു വിധത്തിൽ പറഞ്ഞാൽ, ലാഭം പരമാവധിയാകുന്ന ഉല്പന്ന ബിന്ദുവിൽ MC വർധി ക്കണം. MC കുറഞ്ഞുകൊണ്ടിരിക്കുമ്പോൾ ഉല്പന്നത്തിന്റെ അളവ് വർധിപ്പിച്ചുകൊണ്ട് സ്ഥാപനത്തിന് ലാഭം പരമാവധിയാക്കാൻ കഴിയും. അതായത് MC ആദ്യം കുറഞ്ഞ് പിന്നെ വർധിക്കുമ്പോൾ വിലയ്ക്കു തുല്യമാകുന്ന ഉല്പന്നതലമാണ് സന്തുലിത ഉല്പന്നം. ഡയഗ്രം 4.6 ൽ ഉല്പന്നം Q0 ആയപ്പോൾ E എന്ന ബിന്ദുവിൽ വിലയും MC യും തുല്യമാണ്. ഇവിടെ MC വർധിക്കുന്ന അവസ്ഥയാണ്. അതുപോലെ Q1 ഉല്പന്ന തലത്തിൽ E1 എന്ന ബിന്ദുവിൽ വിലയും MC യും തുല്യമാണ്. പക്ഷേ MC കുറയുന്നു. അതുകൊണ്ട് Q1 സന്തുലിത ഉല്പന്നതലമല്ല. E എന്ന ബിന്ദുവിൽ MC വക്രം വിലരേഖയ താഴെനിന്നും മുകളിലേക്ക് ഖണ്ഡിക്കുന്നു.
വ്യവസ്ഥ 3: വ്യവസ്ഥ മൂന്നിന് രണ്ട് ഭാഗങ്ങളുണ്ട്. ഭാഗം ഒന്ന് ഹ്രസ്വകാലത്തേക്കും ഭാഗം രണ്ട് ദീർഘ കാലത്തേക്കും ആണ്.
ഭാഗം 1: വില ഹ്രസ്വകാലയളവിൽ ശരാശരി വിഭേദക ചെലവിനു തുല്യമോ അതിൽ കൂടുതലോ ആയിരിക്കണം (P ≥ AVC in the short run).
ശരാശരി വിഭേദക ചെലവിനേക്കാൾ താഴ്ന്ന വിലയ്ക്ക് സ്ഥാപനം ഉല്പന്നം ഉല്പാദിപ്പിക്കില്ല. ഡയഗ്രം 4.7 ൽ Q1 അളവ് ഉല്പന്നത്തിൽ വില P, AVC യേക്കാൾ താഴെയാണ്.

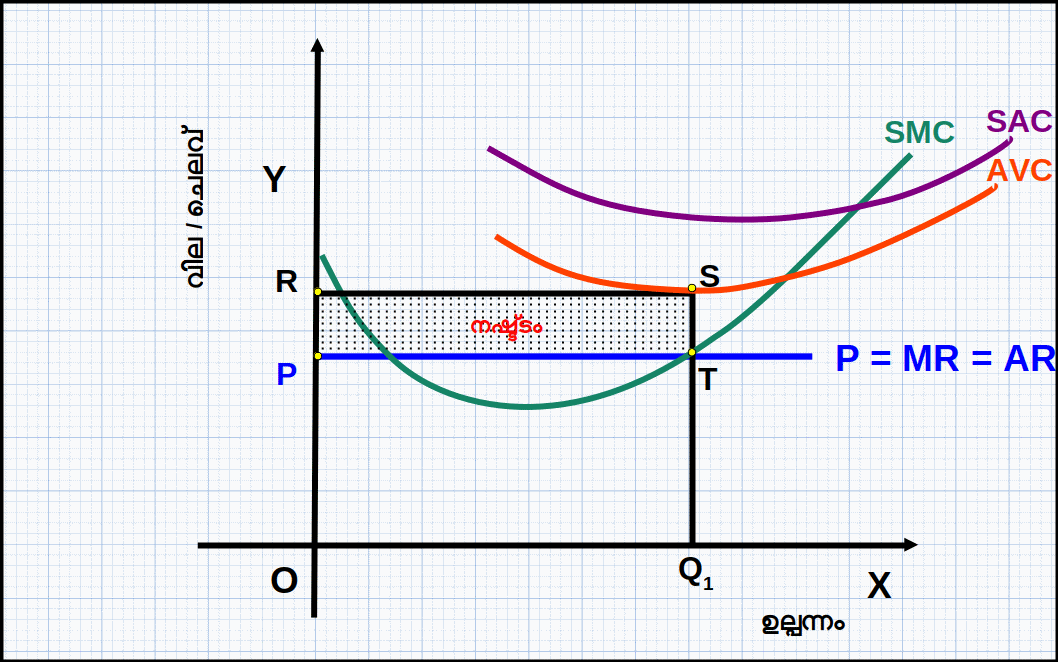
Firm in Loss

Diagram 4.7

Q എന്ന ഉല്പന്ന തലത്തിലെ TR:

TR = വില × ഉല്പന്നത്തിന്റെ അളവ്
= OP × OQ1 = OPTQ1 എന്ന മേഖല.

അതുപോലെ, Q1, ഉല്പന്ന തലത്തിലെ TVC:

TVC = AVC × q
= OR × OQ1 = ORSQ1 എന്ന മേഖല.

മൊത്തം ചെലവ് TFCയും TVCയും ചേർന്നതായതുകൊണ്ട് സ്ഥാപനത്തിന്റെ ലാഭം (Π):

Π = TR - TC = TR - (TFC + TVC)
= TR - TFC - TVC
OPTQ1 - ORSQ1 - TFC

ഇവിടെ വരുമാനത്തേക്കാൾ ചെലവ് കൂടുതലായതുകൊണ്ട് സ്ഥാപനത്തിന് നഷ്ടമായിരിക്കും. ഉല്പന്നം പൂജ്യമാണെങ്കിൽ സ്ഥാപനത്തിന്റെ TRഉം TVCയും പൂജ്യമാകുകയും ലാഭം (-) TFC ആയിരിക്കുകയും ചെയ്യും. അതായത് സ്ഥാപനത്തിന് TFC ക്ക് തുല്യമായ നഷ്ടം സംഭവിക്കുന്നു. അതു കൊണ്ട് സ്ഥാപനം വില AVC യെക്കാൾ കുറവാണെങ്കിൽ ഉല്പാദനം നടത്തുകയില്ല.

ഹ്രസ്വ കാലയളവിൽ ഉല്പന്നത്തിന്റെ വില ശരാശരി വിഭേദക ചെലവിന്റെ മിനിമത്തിനു തുല്യമോ അതിൽ കൂടുതലോ ആയിരിക്കണം (P ≥ minimum of AVC). ഡയഗ്രം 4.8 ൽ Q0 എന്ന ഉല്പന്ന തലത്തിൽ E എന്ന ബിന്ദുവിൽ വില ശരാശരി വിഭേദക ചെലവിന്റെ മിനിമത്തിന് തുല്യമാണ്. ഹ്രസ്വകാലയളവിൽ ഉല്പാദനം നടന്നില്ലെങ്കിൽ ഉല്പാദകന്റെ നഷ്ടം TFC ക്ക് തുല്യമാണ്. വില AVC യ്ക്ക് താഴെയാണെങ്കിൽ നഷ്ടം TFC യേക്കാൾ കൂടുതലായിരിക്കും. അതുകൊണ്ട് AVC യ്ക്ക് താഴെയുള്ള വിലയ്ക്ക് ഉല്പാദിപ്പിക്കുന്നതിനേക്കാൾ നല്ലത് ഉല്പാദനം നിർത്തുന്നതാണ്. എന്നാൽ വില AVC യുടെ മിനിമത്തിലാണെങ്കിൽ നഷ്ടം TFC ക്ക് മാത്രമാണ്. ഈ അവസ്ഥയിൽ ഉല്പാദനം നടത്തുന്നതാണ് നല്ലത്. വില AVCയുടെ മിനിമം പോയിന്റിന് മുകളിലാണെങ്കിൽ ഉല്പാദനം വർധിപ്പിച്ച് നഷ്ടം കുറയ്ക്കാൻ കഴിയും. അതുകൊണ്ട് ഹ്രസ്വകാലയളവിൽ ഉല്പന്നത്തിന്റെ വില AVC യുടെ മിനിമമോ അതിൽ കൂടുതലോ ആയിരിക്കണം.

Normal-Profit

Diagram 4.8

ഭാഗം 2: ദീർഘകാലയളവിൽ വില ശരാശരി ചെലവിനു തുല്യമോ അതിൽ കൂടുതലോ ആയിരിക്കണം(P ≥ LRAC in the long run). ദീർഘകാലയളവിൽ ദീർഘകാല ശരാശരി ചെലവിനേക്കാൾ താഴ്ന്ന വിലയ്ക്ക് സ്ഥാപനം ഉല്പന്നം ഉല്പാദിപ്പിക്കുകയില്ല. ഡയഗ്രം 4.9 ൽ Q1 ഉല്പന്ന തലത്തിൽ TR OPTQ1 എന്ന മേഖലയും TC ORSQ1 എന്ന മേഖലയുമാണ്.
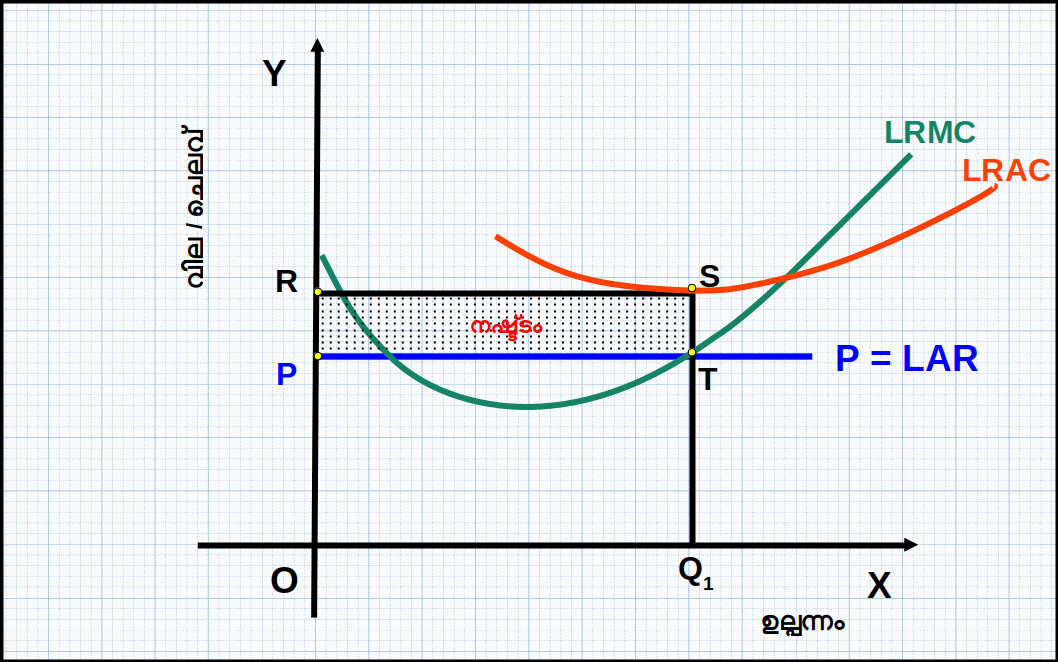
അപ്പോൾ, ലാഭം

л = TR - TC
= OPTQ1 - ORSQ1
= (-) PRST (ORSQ1 OPTQ1)

Long-Run-Loss

Diagram 4.9

TC, TR നെക്കാൾ കൂടുതലായതുകൊണ്ട് ഉല്പന്ന തലത്തിൽ സ്ഥാപനത്തിന്റെ നഷ്ടം PRST ആണ്. അതുകൊണ്ട് Q1 ഉല്പന്നം ലാഭം പരമാവധിയായ ഉല്പന്നതലമല്ല. ദീർഘകാലയളവിൽ സ്ഥാപനത്തിന് നഷ്ടമാണെങ്കിൽ സ്ഥാപനം അടച്ചുപൂട്ടേണ്ടി വരുന്നു.

ദീർഘകാലയളവിൽ വില ശരാശരി ചെലവിന്റെ മിനിമത്തിനു തുല്യമോ അതിൽ കൂടുതലോ ആയിരിക്കണം. വില LRAC തുല്യമാണെങ്കിൽ സ്ഥാപനം ലാഭ-നഷ്ട രഹിതത്തിലായിരിക്കും. ഈ അവസ്ഥയിൽ സ്ഥാപനത്തിന് സാധാരണ ലാഭം ഉണ്ടായിരിക്കും. ഡയഗ്രം 4.10 ൽ Q0 ഉല്പന്ന തലത്തിൽ TC യും TR ഉം തുല്യമാണ്.

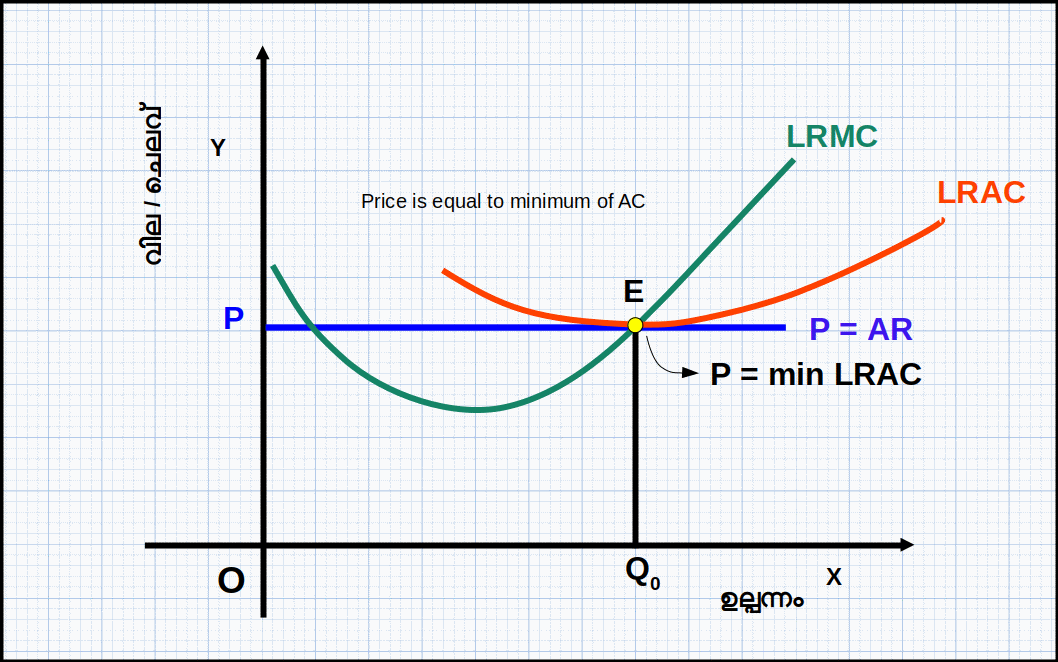
Long-Run-Normal-Profit

Diagram 4.10

л = TR - TC = OPEQ0 - OPEQ0 = 0

ലാഭം പരമാവധിയാക്കൽ: ഗ്രാഫിക്കൽ അവതരണം (PROFIT MAXIMISATION PROBLEM: GRAPHICAL REPRESENTATION)

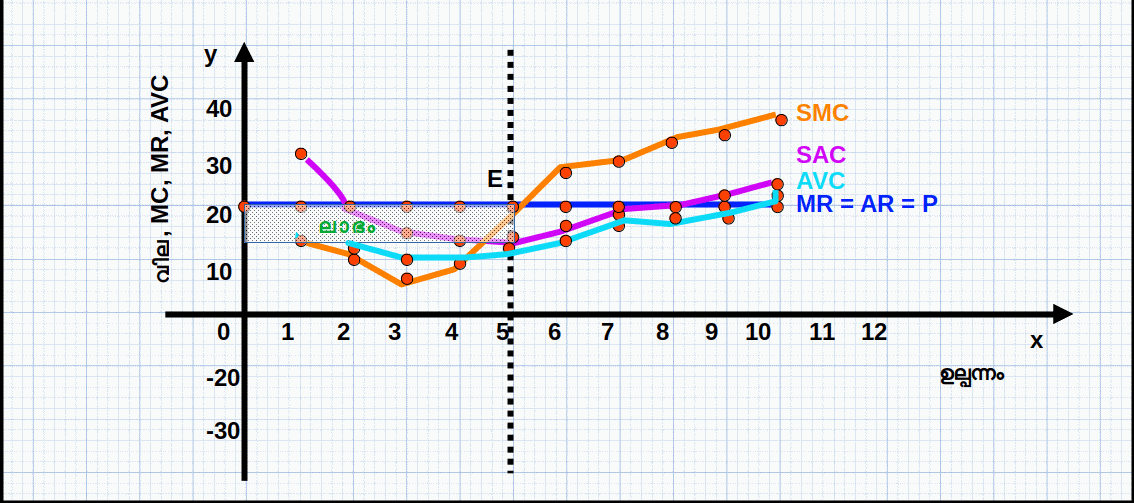
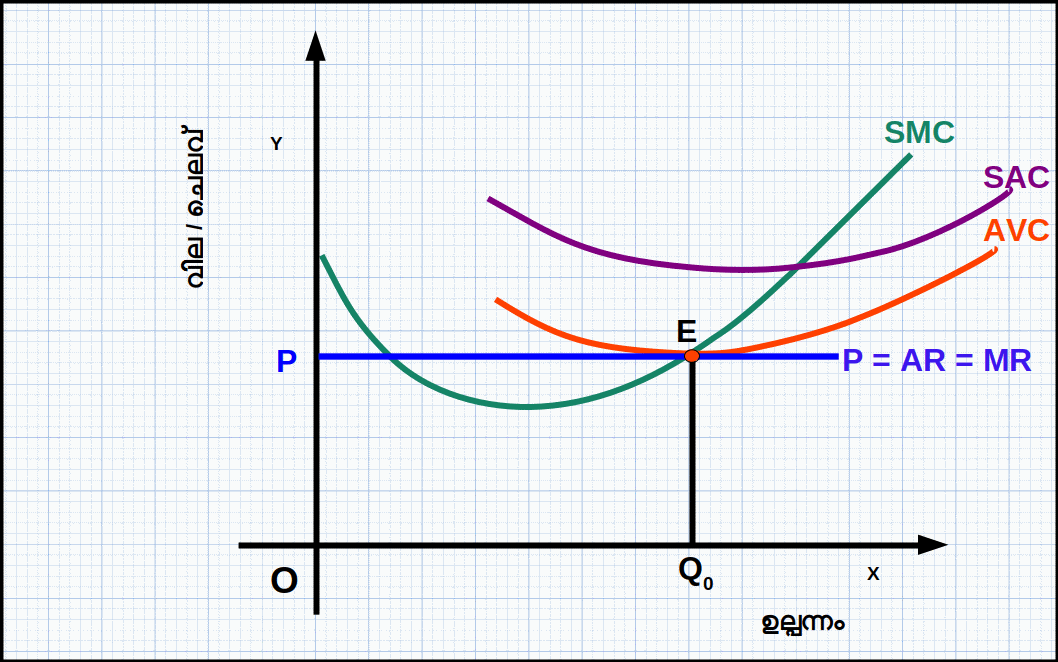
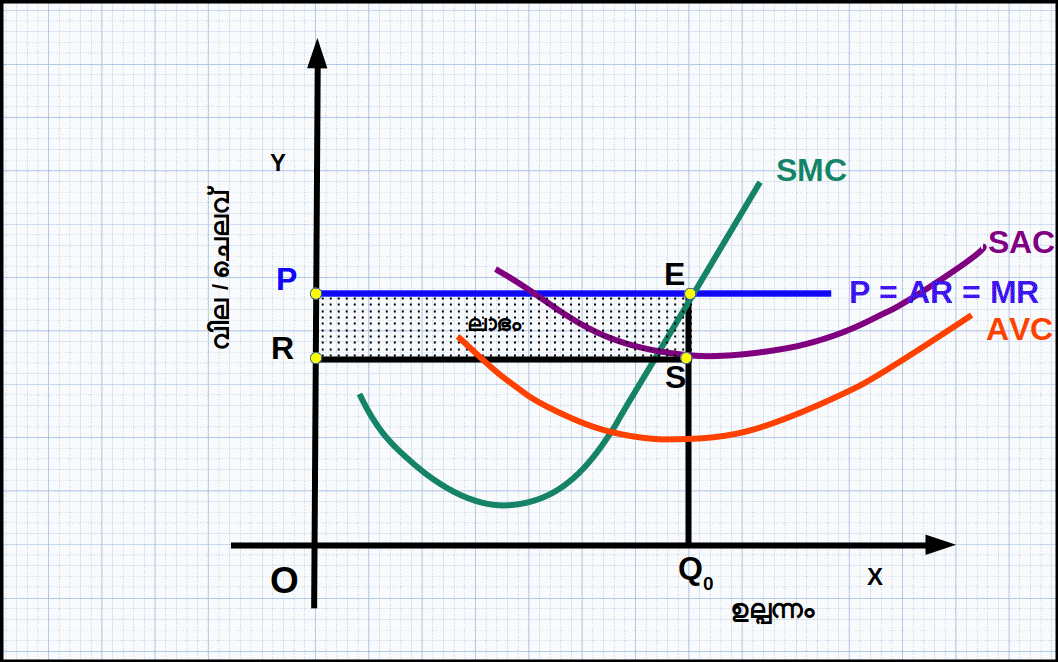
ഹ്രസ്വകാലയളവിൽ സമ്പൂർണ കിടമത്സര കമ്പോളത്തിലെ ഒരു സ്ഥാപനം ലാഭം പരമാവധിയാക്കുന്നത് ഒരു ഡയഗ്രത്തിന്റെ സഹായത്തോടെ വിവരിക്കാം. ഡയഗ്രം 4.11 ൽ Q0 എന്ന ഉല്പന്ന തലത്തിൽ സ്ഥാപനം സന്തുലിതാവസ്ഥയിലാണ്. E എന്ന ബിന്ദുവിൽ മൂന്ന് വ്യവസ്ഥകളും പാലിക്കപ്പെടുന്നു. അതായത്, Q0 ഉല്പന്ന തലത്തിൽ
  • 1. P = MR = MC ആണ്.
  • 2. SMC കുറഞ്ഞുകൊണ്ടിരിക്കുന്നില്ല
  • 3. P ≥ AVC യാണ്
Abnormal-Profit

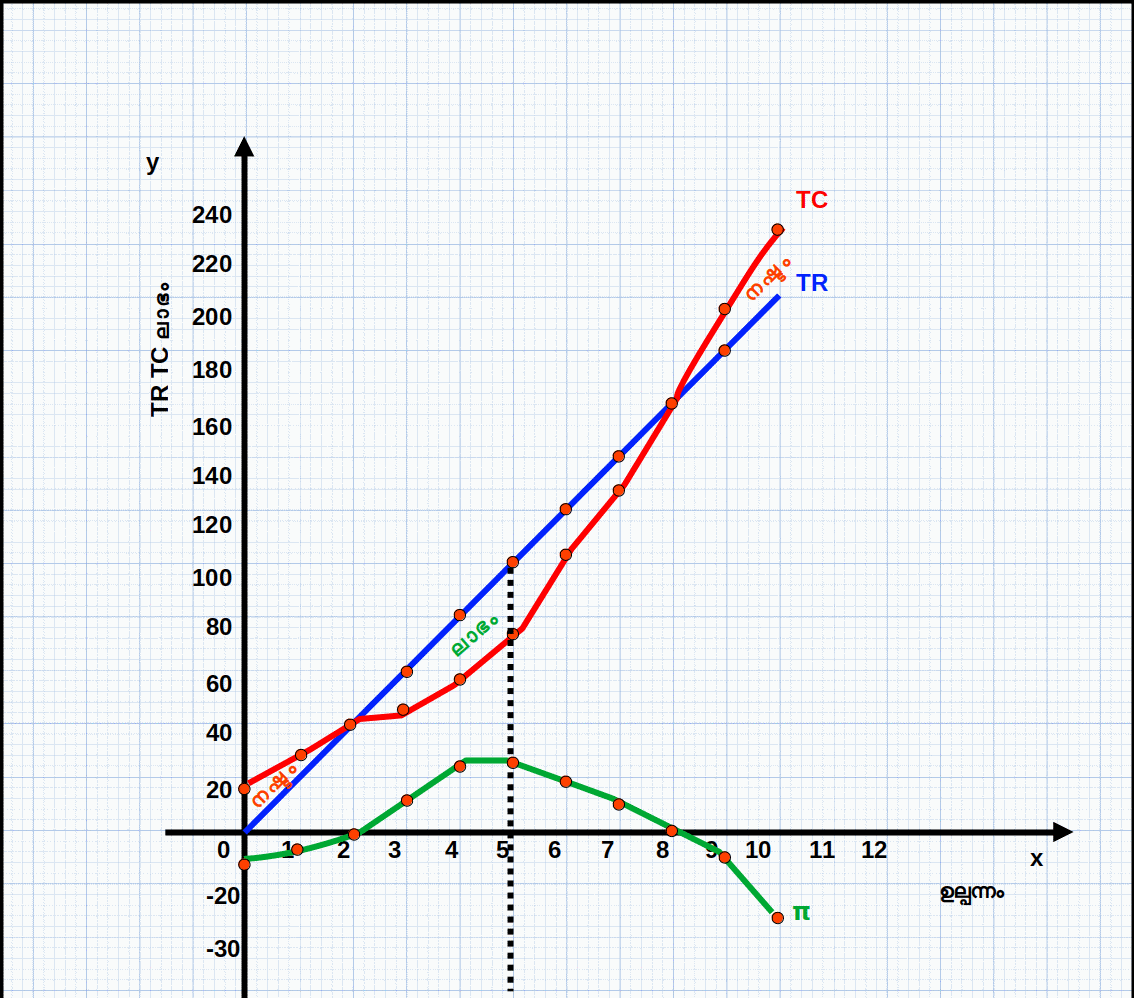
Diagram 4.11

Q0 ഉല്പന്ന തലത്തിൽ TR OPEQ0 ഉം TC ORSQ0, ആണ്. OPEQ0 ൽ നിന്ന് ORSQ0 കുറച്ചാൽ RPES ആണ് ലാഭം.

TR, TC വക്രങ്ങൾ ഉപയോഗിച്ച് ലാഭം പരമാവധിയാക്കുന്ന ജ്യാമിതീയ അവതരണം

താഴെ കൊടുത്തിരിക്കുന്ന ഡയഗ്രത്തിന് മൂന്ന് ഭാഗങ്ങളുണ്ട്. ഒന്നാമത്തെ ഭാഗത്ത് TR, TC പ്രകങ്ങൾ കൊടുത്തിരിക്കുന്നു. രണ്ടാമത്തെ ഭാഗത്ത് MR, MC വക്രങ്ങൾ കൊടുത്തിരിക്കുന്നു. മൂന്നാമത്തെ ഭാഗത്ത് ലാഭ വക്രം കൊടുത്തിരിക്കുന്നു.

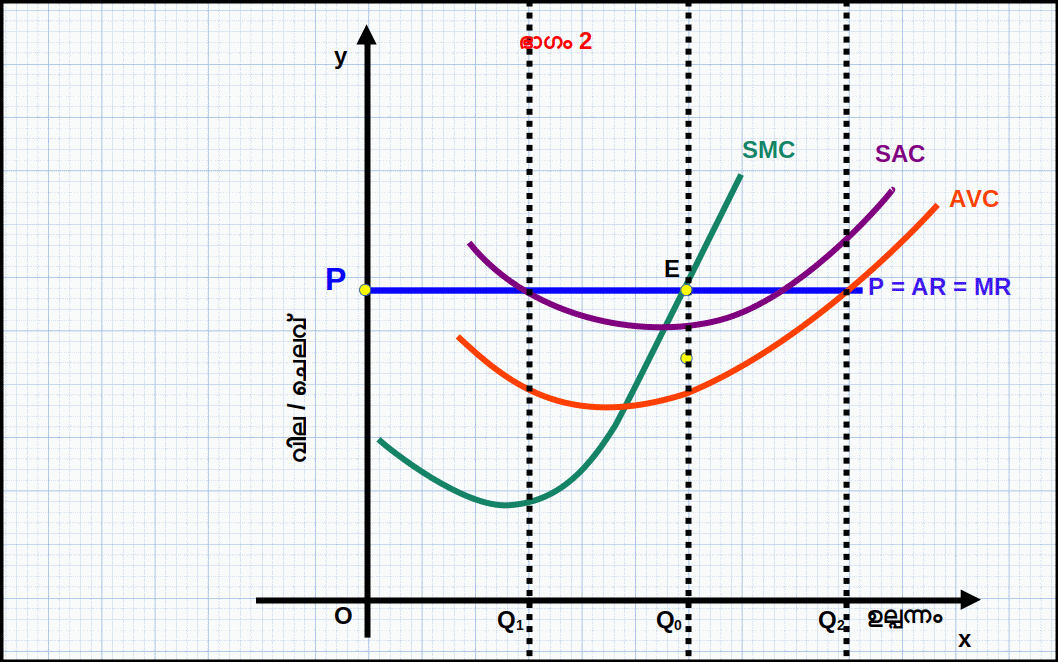
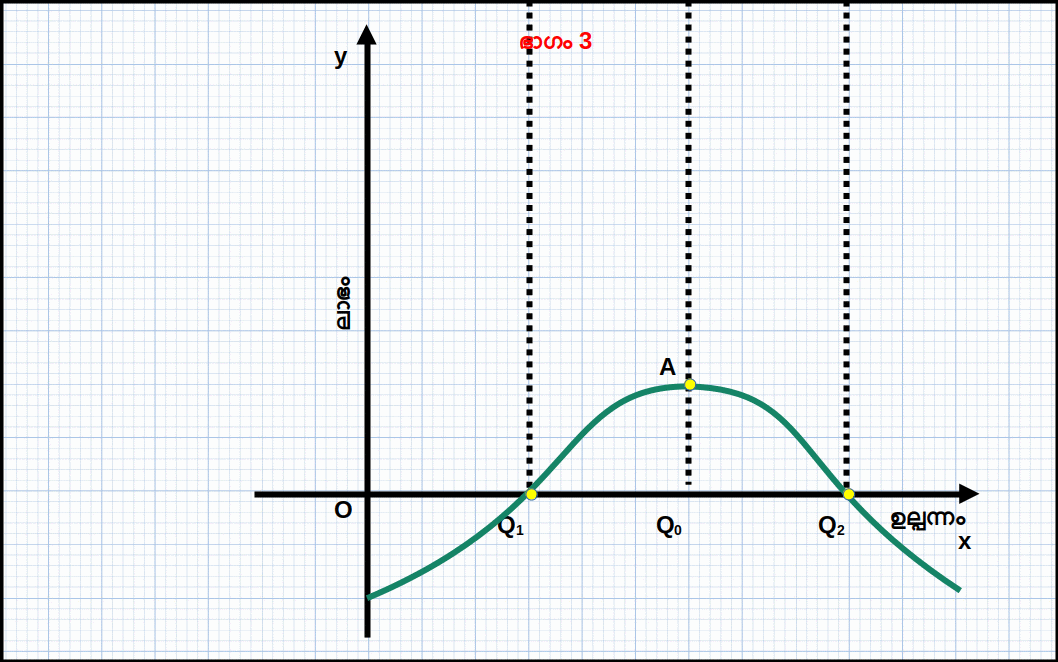
TR-TC-Profit-Maximisation TR-TC-Profit-Maximisation TR-TC-Profit-Maximisation
Diagram 4.12

TR പൂജ്യത്തിൽ തുടങ്ങി ഉല്പന്നത്തിനനുസരിച്ച് വർധിക്കുന്നു. TC, TFC യിൽ നിന്ന് തുടങ്ങി ഉല്പന്നത്തിനനുസരിച്ച് വർധിക്കുന്നു. TC ഉല്പന്നം Q1 വരെ വർധനനിരക്കു കുറഞ്ഞും അതിനുശേഷം വർധന നിരക്ക് കൂടിയും വരുന്നു. E1 എന്ന ബിന്ദുവിൽ TR ഉം TC യും തുല്യമാണ്. E1 ബിന്ദുവിനു മുമ്പ് TR നെക്കാൾ കൂടുതലാണ് TC. അപ്പോൾ л വക്രം നെഗറ്റീവാണ്. TR = TC ആയപ്പോൾ ലാഭം പൂജ്യമാണ്. E2 എന്ന ബിന്ദുവിലും TR ഉം TC യും തുല്യമാണ്. അതിനുശേഷം TC > TR ആണ്. അപ്പോഴും ലാഭം നെഗറ്റീവാണ്. Q0 എന്ന ഉല്പന്ന തലത്തിൽ TR ഉം TC യും തമ്മിലുള്ള വ്യത്യാസം (വെർട്ടിക്കൽ അകലം) ഏറ്റവും കൂടിയിരിക്കുന്നു. ഇവിടെ TR > TC ആണ്. അപ്പോൾ ലാഭ വക്രം` വർധിച്ച് പരമാവധി A എന്ന ബിന്ദുവിൽ എത്തിയിരിക്കുന്നു. Q0 ഉല്പന്നത്തിൽ P = MC ആണ്. അതുകൊണ്ട് സ്ഥാപനം സന്തുലിതാവസ്ഥയിലാണ്. മറ്റ് ഏത് ഉല്പന്ന തലത്തിലും ലാഭം പരമാവധിയായിരിക്കുന്നില്ല. സന്തുലിത ഉല്പന്നത്തിൽ വില AVC യെക്കാൾ കൂടുതലാണ്. അതുപോലെ MC കുറയുകയല്ല ചെയ്യുന്നത്.

Eg 4.5: സമ്പൂർണ കിടമത്സര കമ്പോളത്തിൽ ഒരു സ്ഥാപനം സന്തുലിതാവസ്ഥ നേടുന്ന മൂന്ന് വ്യവസ്ഥകൾ കാണിക്കുന്ന ഒരു പട്ടിക താഴെ കൊടുത്തിരിക്കുന്നു.

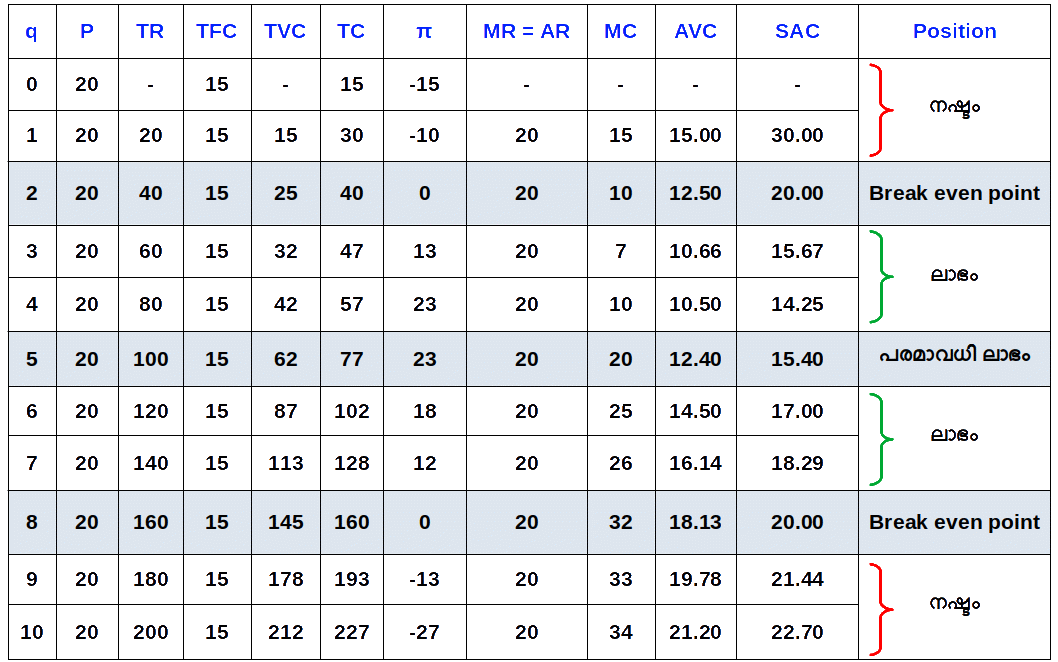
Table

പട്ടിക 4.4 ൽ ഉല്പന്നം 0, 1 എന്നീ യൂണിറ്റുകളിൽ TC, TR നേക്കാൾ കൂടുതലാണ്. അപ്പോൾ സ്ഥാപനത്തിന്റെ ലാഭം നെഗറ്റീവാണ്, അതായത് നഷ്ടം. ഉല്പന്നത്തിന്റെ അളവ് 2 യൂണിറ്റായപ്പോൾ TC യും TR ഉം തുല്യമാണ്. അപ്പോൾ ലാഭം പൂജ്യമാണ്. രണ്ടാമത്തെ യൂണിറ്റ് മുതൽ ഏഴാമത്തെ യൂണിറ്റ് വരെ TR, TC യെക്കാൾ കൂടുതലാണ്. അപ്പോൾ ലാഭം പോസിറ്റീവാണ്. എട്ടാമത്തെ യൂണിറ്റിൽ TR ഉം TC യും വീണ്ടും തുല്യമാകുകയും ലാഭം പൂജ്യമാകുകയും ചെയ്യുന്നു. അതിനുശേഷം TR നേക്കാൾ TC കൂടുതലാകുന്നു. ഇവിടെ ലാഭം നെഗറ്റീവാണ്.
ഉല്പന്നത്തിന്റെ അളവ് 4 ലും 5 ലും എത്തുമ്പോൾ TR ഉം TC യും തമ്മിലുള്ള വ്യത്യാസം അഥവാ അകലം ഏറ്റവും കൂടിയിരിക്കുന്നു. അപ്പോൾ ലാഭം 23 യാണ്. ഇതാണ് ഏറ്റവും ഉയർന്ന ലാഭം. 5-ാമത്തെ ഉല്പന്ന യൂണിറ്റിലാണ് വിലയും (MR) MC യ്ക്ക് തുല്യമാകുന്നത് (P = MR = MC = 20). മാത്രമല്ല, 5-ാമത്തെ യൂണിറ്റിൽ MC കുറയുകയല്ല (വർധിക്കുകയാണ്). അതുപോലെ വില 20 എന്നത് AVC 12.40 എന്നതിനേക്കാൾ ഉയർന്നതാണ്. സമ്പൂർണ കിടമത്സര കമ്പോളത്തിന്റെ സന്തുലിതാവസ്ഥയുടെ മൂന്ന് വ്യവസ്ഥകളും പാലിക്കുന്നതുകൊണ്ട് സ്ഥാപനത്തിന് പരമാവധി ലാഭം ലഭിക്കുന്നത് 5-ാമത്തെ ഉല്പന്ന യൂണിറ്റിലാകുമ്പോഴാണ്. അതു കൊണ്ട് സന്തുലിത ഉല്പന്നം 5 ഉം സന്തുലിത വില 20 യുമാണ്.

Diagram Diagram

Diagram 4.13