On the basis of the type of data series that has provided to us (ie, Individual, Discrete, Continuous), it will be convenient if we use appropriate formula for finding averages in each of these series.

There are three methods by which Simple mean can be calculated in each of these three series.

They are :

1. Direct Method
2. Assumed Mean Method
3. Step Deviation Method

Calculation of arithmatic mean can be studied under two heads.

1. Arithmetic Mean for Ungrouped Data
2. Arithmetic Mean for Grouped Data

Arithmetic Mean for Ungrouped data can be calculated using the following methods:

1. Direct Method
2. Assumed Mean Method
3. Step Deviation Method

STEPS

1. Find the sum of observations (∑X)
2. Take the number of observations (N)
3. Use the formula \( X̅ = {{{\frac{ΣX}{N}} }} \)

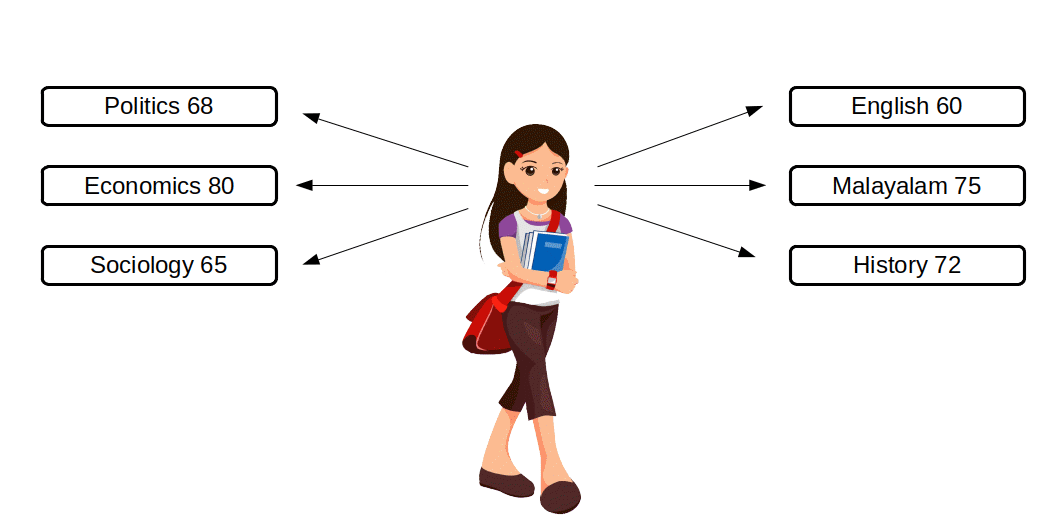$$ A.M = {{{\frac{60+75+72+68+80+65}{6}} }} $$ $$ = {{{\frac{420}{6}} }} = 70 $$

STEPS

1. Take an assumed mean A
2. Take the deviation of each X from the assumed mean. ie., d = X - A
3. Find the sum of the deviations to get Σd
4. Use the formula \( X̅ = A + {{{\frac{Σd}{N}} }} \) ; where N is the total number of observations

Let us find the arithmetic mean of the following 20 observations using assumed mean method.

2500, 6500, 3000, 5500, 4500, 6000, 3500, 3000, 5500, 5000, 2000, 4500, 3500, 3000, 4500, 6500, 4000, 3000, 2500, 4500

Table 5.1
X	d=X-A=X-4000
2500	-1500
6500	2500
3000	-1000
5500	1500
4500	500
6000	2000
3500	-500
3000	-1000
5500	1500
5000	1000
2000	-2000
4500	500
3500	-500
3000	-1000
4500	500
6500	2500
4000	0
3000	-1000
2500	-1500
4500	500
N=20	Σd = (-10000)+13000=3000

$$ {X̅=}A+\frac{Σd}{N} = 4000+\frac{3000}{20} $$

$$=4000 + 150 = 4150 $$

Complexity of calculations in finding arithmatic mean can nfurther be reduced by using step deviation method.

STEPS

1. Take an assumed mean A
2. Take the deviation of each X from the assumed mean. ie., d = X - A
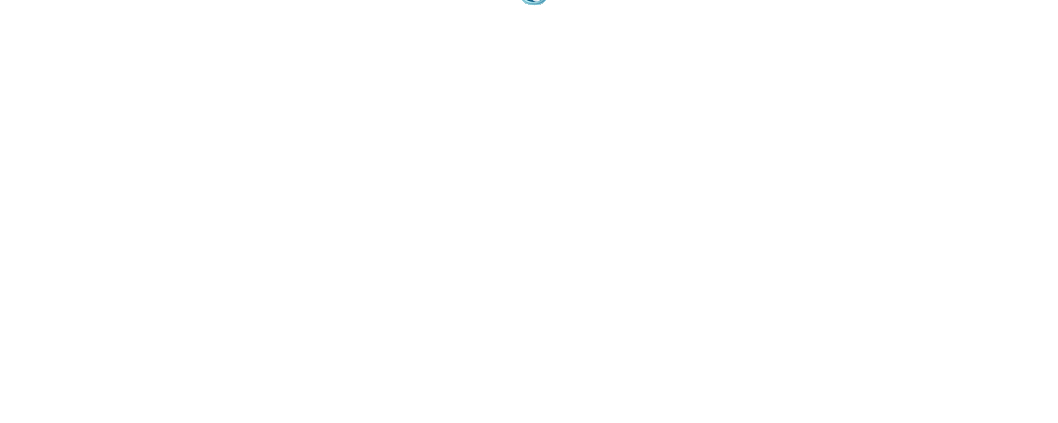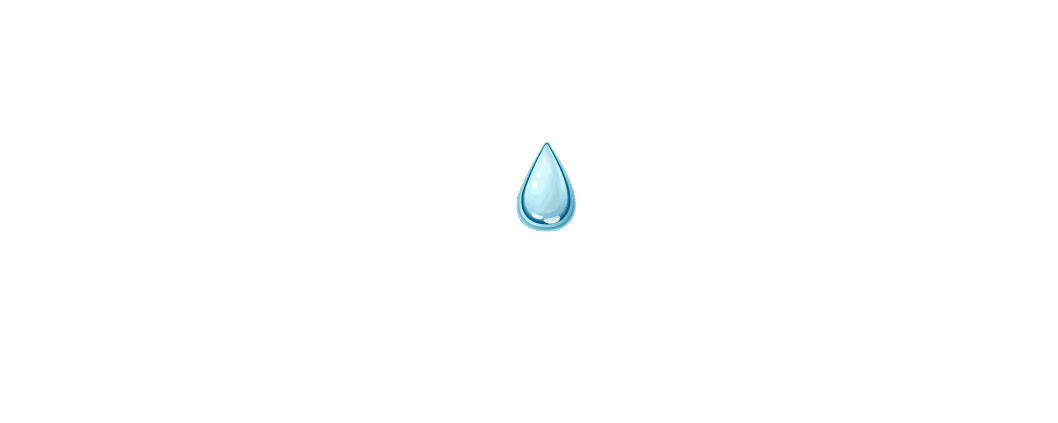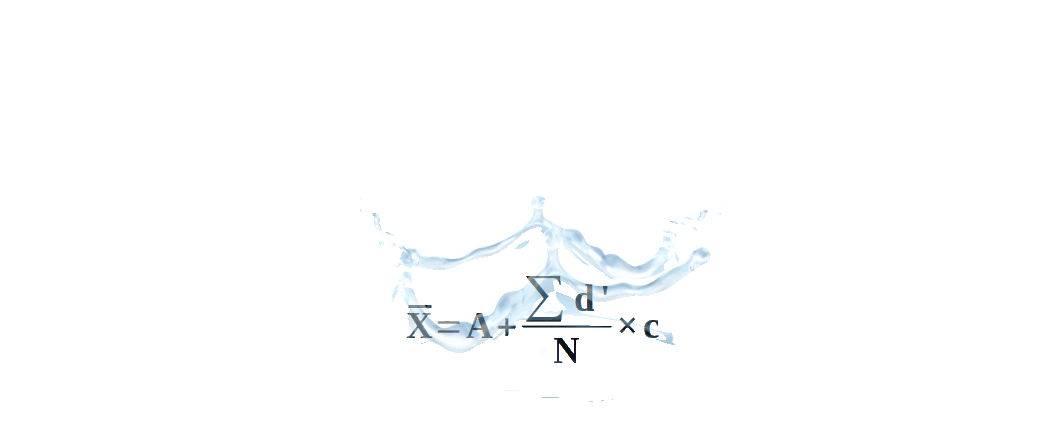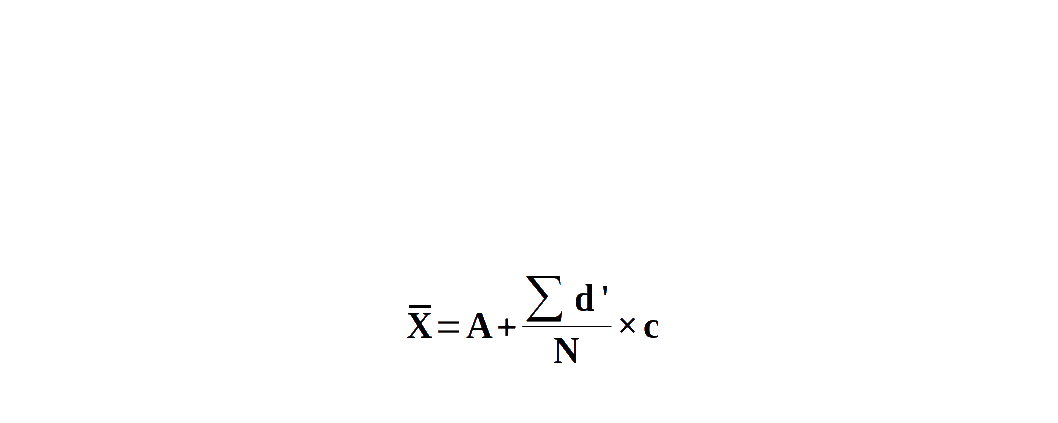
3. Devide the deviation d by common factor c, i.e., \( d ' = {{{\frac{d}{c}} }} = {{{\frac{X - A}{c}} }} \)
4. Then find Σd’
5. Use the formula \( X̅ = A + {{{\frac{Σd'}{N}} }} × c \) ; where N is the total number of observations

Let us find the arithmatic mean of the following 10 obserations using step deviation method.

45, 30, 65, 70, 40, 25, 45, 25, 55, 40, 20, 50

Assumed mean is taken as 50.

Let c = 5 (we decide value of c only after seeing the column for d in the table)

Table 5.2
X	d=X-A=X-50	\( \mathbf {d ' = {{{\frac{d}{c}} }} = {{{\frac{d}{5}} }}} \)
45	-5	-1
30	-20	-4
65	15	3
70	20	4
40	-10	-2
25	-25	-5
45	-5	-1
25	-25	-5
55	5	1
40	-10	-2
20	-30	-6
50	0	0
N = 12		Σd’ = (-26) + 8 =-18

$$ X̅ = A + {{{\frac{Σd'}{N}} }} × c = {50+\frac{-18}{12}} × 5 $$

$$= 42.5 $$

STEPS

1. Multiply the frequency against each observation with the value of observation to get fx
2. Add the column of fx to get Σfx
3. Use the formula \( X̅ = {{{\frac{Σfx}{Σf}} }} \)

From the following data relating to the monthly income of 50 persons, determine the average monthly income using assumed mean method

Table 5.3
Income	Number of Persons
1200	2
1500	10
1800	15
2000	7
2300	5
2600	4
3400	3
4200	3
5000	1

Now we can create a table to find fx.

Table 5.4
Income	Number of Persons	fX
1200	2	2400
1500	10	15000
1800	15	27000
2000	7	14000
2300	5	11500
2600	4	10400
3400	3	10200
4200	3	12600
5000	1	5000
	Σf = 50	Σfx = 108100

$$ X̅ = {{{\frac{Σfx}{Σf}} }} = {\frac{-108100}{50}} $$

$$= 2162 $$

Assumed mean method is applying just to simplify the calculations.

STEPS

1. Take an assumed mean A
2. Take the deviation ‘d’ of each X from the assumed mean. ie., d = X - A
3. Multiply d with f to get fd
4. Add the column of fd to get Σfd
5. Add all the frequencies to get Σf
6. Use the formula \( X̅ = A + {{{\frac{Σfd}{Σf}} }} \)

From the following data relating to the monthly income of 50 persons, determine the average monthly income using assumed mean method.

Table 5.5
Income	Number of Persons
1200	2
1500	10
1800	15
2000	7
2300	5
2600	4
3400	3
4200	3
5000	1

Now we can create a table to find d and fd.

Table 5.6
Income	Number of Persons	d = X-A = X-2300	fd
1200	2	-1100	-2200
1500	10	-800	-8000
1800	15	-500	-7500
2000	7	-300	-2100
2300	5	0	0
2600	4	300	1200
3400	3	1100	3300
4200	3	1900	5700
5000	1	2700	2700
	Σf = 50		Σfd=(-19800)+12900 = -6900

$$ X̅ = A + {{{\frac{Σfd}{Σf}} }} = 2300 + {\frac{-6900}{50}} $$

$$= 2162 $$

Complexity of calculations in finding arithmatic mean can nfurther be reduced by using step deviation method. Under step deviation method, as in the individual series case, we divide the deviations d by a common factor say c. We denote that as d’.

STEPS

1. Take an assumed mean A
2. Take the deviation of each X from the assumed mean. ie., d = X - A
3. Devide the deviation d by common factor c, i.e., \( d ' = {{{\frac{d}{c}} }} = {{{\frac{X - A}{c}} }} \)
4. Multiply each d’ with frequency to get fd’
5. Add the column of fd’ to get Σfd’
6. Add all the frequencies to get Σf
7. Use the formula \( X̅ = A + {{{\frac{Σfd'}{Σf}} }} × c \) ; where N is the total number of observations

From the following data relating to the monthly income of 50 persons, determine the average monthly income using step deviation method.

Table 5.7
Income	Number of Persons
1200	2
1500	10
1800	15
2000	7
2300	5
2600	4
3400	3
4200	3
5000	1

Now we can create a table to find d, d' and fd'. We can take assumed mean as 2300 and c as 100. C is taken as 100 after getting d column.

$$ X̅ = A + {{{\frac{Σfd'}{Σf}} }} × c = 2300 + {\frac{-69}{50}} × 100$$

$$= 2162 $$

STEPS

1. Find the mid value of each class, denoted by m
2. Multiply each class frequency with m to get fm
3. Add the column fm to get Σfm
4. Use the formula \( X̅ = {{{\frac{Σfm}{Σf}} }} \)

Note :-

1. For finding arithmetic mean, it is not necessary to convert inclusive type to exclusive type. However, in case of finding median or; mode the coiwersion .is necessary-
2. If intervals are having unequal width, then also the same method can be followed.
3. If the distribution is exdlusive type, then, the class interval ot a class is got by the formula (upper limit - lower limit)
4. If the distribution is inclusive type, then, there is a gap between the upper limit of the class and the lower limit of the next class. In that case, the class interval of the class is got by the formula, (upper limit - lower limit + gap).

Let us find arithmetic mean of the following distribution by direct method.

Table 5.9
Marks	Number of Students
0-10	8
10-20	12
20-30	15
30-40	17
40-50	25
50-60	20
60-70	16
70-80	13
80-90	10
90-100	4

Let us create a table showing m and fm.

Table 5.10
Marks	Number of Students	m	fm
0-10	8	5	40
10-20	12	15	180
20-30	15	25	375
30-40	17	35	595
40-50	25	45	1125
50-60	20	55	1100
60-70	16	65	1040
70-80	13	75	975
80-90	10	85	850
90-100	4	95	380
	Σf = 140		Σfm = 6660

$$ X̅ = {{{\frac{Σfm}{Σf}} }} = {\frac{6660}{140}} $$

$$= 47.57 $$

Assumed mean method is applying just to simplify the calculations.

STEPS

1. Find the mid value (m) of each class
2. Take an assumed mean, A
3. Take deviation of each m from A, i.e., d = m - A
4. Multiply d with f to get fd
5. Add all fd to get Σfd
6. Add all f to get Σf
7. Apply the formula \( X̅ = A + {{{\frac{Σfd}{Σf}} }} \)

Find arithmetic mean of the following distribution by assumed mean method.

Table 5.11
Marks	Number of Students
0-10	8
10-20	12
20-30	15
30-40	17
40-50	25
50-60	20
60-70	16
70-80	13
80-90	10
90-100	4

Let us create a table showing m, d and fd. Assumed mean is taken as 45.

Table 5.12
Marks	Number of Students	m	d = m-45	fd
0-10	8	5	-40	-320
10-20	12	15	-30	-360
20-30	15	25	-20	-300
30-40	17	35	-10	-170
40-50	25	45	0	0
50-60	20	55	10	200
60-70	16	65	20	320
70-80	13	75	30	390
80-90	10	85	40	400
90-100	4	95	50	200
	Σf = 140			Σfd = -1150 + 1510 = 360

$$ X̅ = A + {{{\frac{Σfd}{Σf}} }} = 45 + {\frac{360}{140}} $$

$$= 47.57 $$

In this method, in order to simplify calculations we take a common factor for the data.

STEPS

1. Find the mid value (m) of each class
2. Take an assumed mean A
3. Take the deviation of each m from A, i.e., d = m-A
4. Divide d by a common factor c to get d’. \( d ' = {{{\frac{d}{c}} }} = {{{\frac{m - A}{c}} }} \)
5. Multiply d’ with f to get Σfd’
6. Add all the frequencies to get Σf
7. Apply the formula \( X̅ = A + {{{\frac{Σfd'}{Σf}} }} × c \)

EXCLUSIVE CLASS

Find arithmetic mean of the following distribution using step deviation method.

Table 5.13
Marks	Number of Students
0-10	8
10-20	12
20-30	15
30-40	17
40-50	25
50-60	20
60-70	16
70-80	13
80-90	10
90-100	4

To find arithmetic mean through step deviation method, we need to find m, d, d' and fd'.

Table 5.14
X	f	m	d = m-45	\( \mathbf {d ' = {{{\frac{d}{c}} }} = {{{\frac{d}{10}} }}} \)	fd'
0-10	8	5	-40	-4	-32
10-20	12	15	-30	-3	-36
20-30	15	25	-20	-2	-30
30-40	17	35	-10	-1	-17
40-50	25	45	0	0	0
50-60	20	55	10	1	20
60-70	16	65	20	2	32
70-80	13	75	30	3	39
80-90	10	85	40	4	40
90-100	4	95	50	5	20
	Σf = 140				Σfd’ = (-115) + 151 = 36

$$ X̅ = A + {{{\frac{Σfd'}{Σf}} }} × c = 45 + {\frac{36}{140}} × 10 $$

$$= 47.57 $$

INCLUSIVE CLASS

Find arithmetic mean of the following distribution using step deviation method. The given distribution is in inclusive format.

Table 5.15
Marks	Number of Students
0-9	1
10-19	5
20-29	12
30-39	15
40-49	24
50-59	20
60-69	9
70-79	8
80-89	4
90-99	2

Here the classes are inclusive type. It is not neccessary to convert them into exclusive, because mid-points remain the same whether or not the adjustment is made. To find arithmetic mean through step deviation method, we need to find m, d, d' and fd'

Table 5.16
X	f	m	d = m-45	\( \mathbf {d ' = {{{\frac{d}{c}} }} = {{{\frac{d}{10}} }}} \)	fd'
0-9	8	4.5	-50	-5	-5
10-19	12	14.5	-40	-4	-20
20-29	15	24.5	-30	-3	-36
30-39	17	34.5	-20	-2	-30
40-49	25	44.5	-10	-1	-24
50-59	20	54.5	0	0	0
60-69	16	64.5	10	1	9
70-79	13	74.5	20	2	16
80-89	10	84.5	30	3	12
90-99	4	94.5	40	4	8
	Σf = 140				Σfd’ = (-115) + 45 = -70

$$ X̅ = A + {{{\frac{Σfd'}{Σf}} }} × c = 54.5 + {\frac{-70}{100}} × 10 $$

$$= 47.57 $$

UNEQUAL CLASSES

Let us Find arithmetic mean of the following distribution using step deviation method. Here the distribution is provided with unequal class intervals. If classes are having unequal width, it is not necessary to convert them to equal width.

Table 5.17
Marks	Number of Students
0-5	8
5-15	12
15-20	15
20-40	17
40-50	25
50-60	20
60-65	16
65-80	13
80-90	10
90-100	4

To find arithmetic mean through step deviation method, we need to find m, d, d' and fd'.

$$ X̅ = A + {{{\frac{Σfd'}{Σf}} }} × c = 55 + {\frac{-556}{100}} × 2.5 $$

$$= 45.07 $$

OPEN END CLASSES

Find arithmetic mean of the following distribution using step deviation method.

Table 5.19
Marks	Number of Students
Less than 15	8
15-30	15
30-45	32
45-60	26
60-75	13
Above 75	6

Here the given table has two open end classes, namely. the first and the last. In the case of open end classes, we cannot find out the arithmetic mean unless we make an assumption about the limits of the open end classes. For that, look at the class intervals of the classes following the first class and preceding the last class. The class interval of the second class is 15. Hence by assuming the class interval of the first class also as 15, we get the lower limit of the first class as 0. Similarly, since the class interval of the class preceding to the last class is 15, by assuming the class interval of the last class as 15, we get the upper limit of the last class as 90.

Now we get the adjusted table as given below.

Table 5.20
Marks	Number of Students
0-15	8
15-30	15
30-45	32
45-60	26
60-75	13
75-90	6
Total	100

Now we can simply find arithmetic mean by using any method. Here , we used step deviation method to find arithmetic mean.

$$ X̅ = A + {{{\frac{Σfd'}{Σf}} }} × c = 52.5 + {\frac{-183}{100}} × 5 $$

$$= 43.35 $$

MORE THAN CUMULATIVE FREQUENCIES

Find arithmetic mean of the following distribution using step deviation method.

Table 5.22
Wage	Number of Labourers
Above 0	675
Above 10	625
Above 20	550
Above 30	450
Above 40	275
Above 50	150
Above 60	75
Above 70	25

Here the frequencies given are not the simple frequencies. They are more than cumulative frequencies. Hence we need to convert them to simple frequency. The simple frequency of the first class = 675 — 625 = 50. For the second class, simple frequency = 625 — 550 = 75. For the third class, simple frequency = 550 — 450 = 100; and so on. Also we should write the classes accordingly.

Now we get the adjusted table as given below.

Table 5.23
X	f
0-10	50
10-20	75
20-30	100
30-40	175
40-50	125
50-60	75
60-70	50
70-80	25
Total	675

Now we can find arithmetic mean using step deviation method.

$$ X̅ = A + {{{\frac{Σfd'}{Σf}} }} × c = 35 + {\frac{125}{675}} × 10 $$

$$= 36.85 $$

LESS THAN CUMULATIVE FREQUENCIES

Find arithmetic mean of the following distribution using step deviation method.

Table 5.25
Mark	Number of Students
Less than 10	4
Less than 20	16
Less than 30	40
Less than 40	76
Less than 50	96
Less than 60	112
Less than 70	120
Less than 80	125

By inspection, we can see that the frequencies given are not the simple frequencies. They are less than cumulative frequencies. In order to calculate arithmetic mean, we need simple frequency of each class. So first we need to convert cumulative frequencies to simple frequency. The simple frequency of the first class is 4 itself. For the second class, simple frequency = 16 — 4 = 12. For the third class, simple frequency = 40 — 16 = 24; and so on. Also we should write the classes accordingly.

Now we get the adjusted frequencies as in the table given below.

Table 5.26
X	f
0-10	4
10-20	12
20-30	24
30-40	36
40-50	20
50-60	16
60-70	8
70-80	5
Total	125

Now we can find arithmetic mean using step deviation method.

Table 5.27
X	f	m	d = m-35	\( \mathbf {d ' = {{{\frac{d}{c}} }} = {{{\frac{d}{10}} }}} \)	fd'
0-10	4	5	-30	-3	-12
10-20	12	15	-20	-2	-24
20-30	24	25	-10	-1	-24
30-40	36	35	0	0	0
40-50	20	45	10	1	20
50-60	16	55	20	2	32
60-70	8	65	30	3	24
70-80	5	75	40	4	20
	Σf = 125				Σfd’=(-60)+96 = 36

$$ X̅ = A + {{{\frac{Σfd'}{Σf}} }} × c = 35 + {\frac{36}{125}} × 10 $$

$$= 37.88 $$

COMBINED MEAN

Consider a sample 20, 23, 15, 21, 28 and 19. We can call this as sample - I. Its arithmetic mean is :

Consider another sample 32, 28, 19 and 13. Let us call it as sample - II. Its arithmetic mean is :

Let us find out the arithmetic mean of combined sample.

We can find the combined mean of samples without knowing the individual observations. We only need to know the sizes and means of each sample to find out the combined mean. Suppose that we do not know the individual observations of sample-I and sample- II above, and we only know the sizes of samples and their means. Let size of sample-I as n₁ and size of sample-II as n₂, ; Also, we denote the mean of sample- I as X̄₁ and mean of sample- II as X̄₂,. Then the combined mean X̄ of samples.1 and 2 can be determined using the formula:

Let us find combined mean for given data as n₁ = 6, n₂ = 4, X̅₁ = 21 and X̅₂ = 23.

CORRECTION IN MEAN

While calculating mean, sometimes we may consider numbers wrongly by mistake. This will lead to wrong results. But, when we realized the mistake, the results may be corrected without doing the problem afresh. The process of finding out the correct mean value is very simple. First we multiply the incorrect mean by the total number of observations. The incorrect values are then subtracted from that and the correct values are added, Then divide the number you have got by the total number of observations. The below given example will illustrate the method.

The average mark secured by 50 students was calculated as 48. later on, it was found that a mark 60 was misred as 16. Find the correct average mark secured by the students.

WEIGHTED MEAN

The arithmetic mean we had studied is simple arithmetic mean. In the calculation of simple arithmetic mean each item of the series is considered equally important. But there may be cases where all items may not have equal importance. Some of them may be comparatively more important than others. For example, if we are finding out the change in the cost of living of a certain group of people and if we merely find the simple arithmetic average of the prices of the commodities consumed by them, the average would be unrepresentative. All the items of consumption are not equally important. The price of salt may increase by 100 per cent but this will not affect the cost of living to the extent to which it would be affected, if the price of rice goes up only by 10 per cent. In such cases simple average is not suitable and we give different weights to each item while computing average. Arithmetic mean computed by assigning different weights to each item is called weighted arithmetic mean.

Let x₁, x₂, .... , x_n be n items with weights w₁, w₂, ... , w_n respectively. Then the weighted arithmetic mean is:

$$ { X̅_w =\frac{w_1 x_1 + w_2 x_2 +...+ w_n x_n}{w_1 + w_2 +...+ w_n} = \frac{Σwx}{Σw}} $$

Let us find weighted arithmatic mean of the given data.

Table 5.28
Item	Amount	Weight
1	35	3
2	27	7
3	65	1
4	47	4
5	30	9

Now we need to create a table with w and wx as given below.

Table 5.29
x (Amount)	w (Weight)	wx
35	3	105
27	7	189
65	1	65
47	4	188
30	9	270
	Σw 24 = 24	Σwx = 817

$$ { X̅_w =\frac{Σwx}{Σw} = \frac{817}{24}} = 34.04 $$

Let us practice an another example.

An examination in the subjects, English, Mathematics and Social Science was held to decide the award of a scholarship. The marks obtained by the top three candidates are given below. We can find out who is going to win the scholarship.We can find out the possibility of change in the selection of student, if we use simple arithmetic mean for selection.

Let us create a table showing wx for each student.

Now we can calculate weighted and simple mean

If weighted mean is considered, student - 3 will get scholarship. But if we consider simple mean, then, student -1 will be selected for scholarship.

AN INTERESTING PROPERTY OF AM

It is interesting to note that the sum of deviations of items in a series about arithmetic mean is always equal to zero.

Symbolically, Σ(X - X̅) = 0

However, arithmetic mean is affected by extreme items. That is, any large value on either end, can push it up or down.

Consider 6 items 20, 23, 15, 21, 28 and 19. Its arithmetic mean is 21. Their deviation from the arithmetic mean are -1, 2, -6, 0, 7, and -2 respectively.

Then, the sum of the deviations = (-1) + 2 + (-6) + 0 + 7 + (-2) = 0

• It is the most popular average
• It is easy-to understand
• It is based on all items of the series
• It is not very much affected by sampling fluctuations
• It is capable of further algebraic treatment
• It is not a positional value
• It is rigidly defined so as to avoid ambiguity

• It cannot be determined by inspection
• It cannot be determined graphically
• It is affected by extreme values
• It is not suitable for averaging ratios or percentages
• It cannot be determined if one of the observations is missing
• It may not be a number in the series
• For open-end classes, assumptions may be made about the class interval