Now we understood that median of a distribution is that value which divides the distribution in to two equal parts. We can also find three values which divide the distribution in to four equal parts. These three values are called the quartiles. Likewise we can find nine values which divide the distribution in to ten equal parts. These nine values are called deciles. In a similar manner we can define percentiles. Percentiles are ninety nine values which divide the distribution in to hundred equal parts.

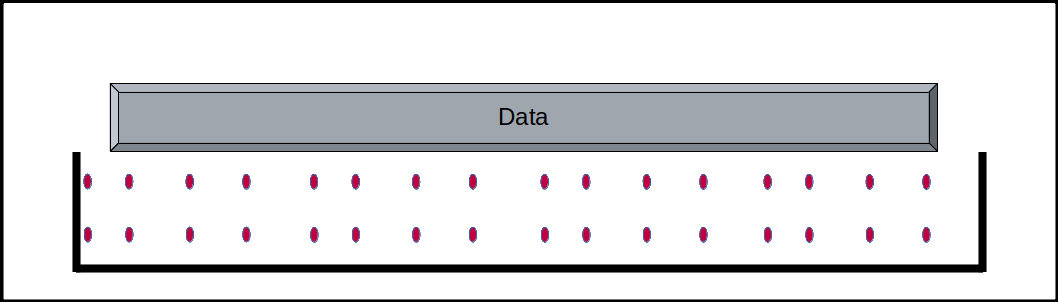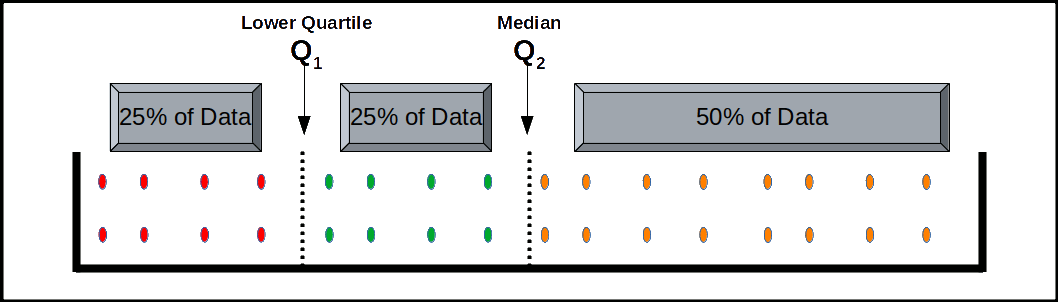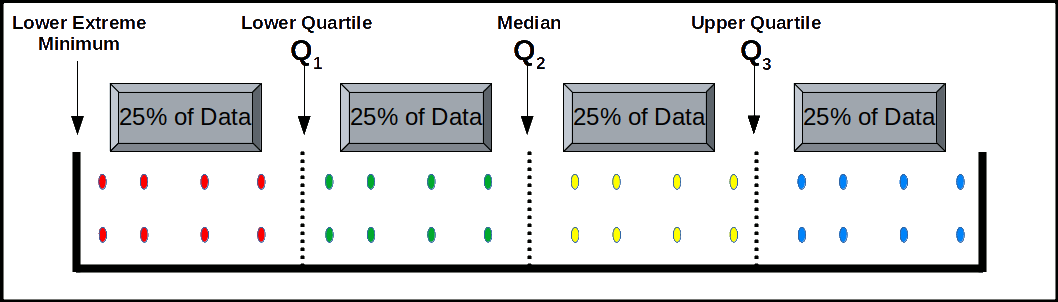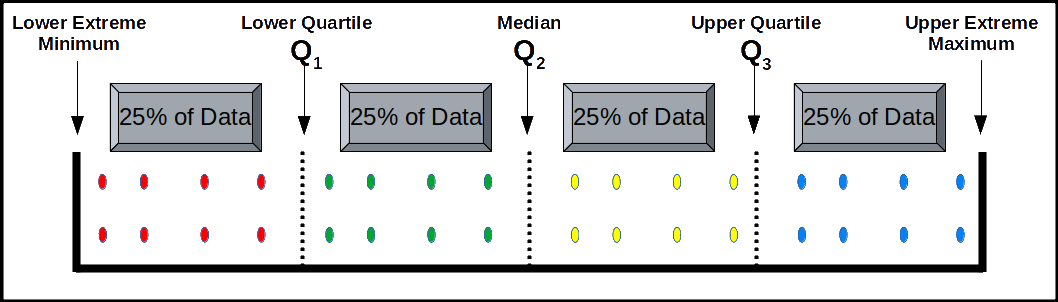
Quartiles are those values which divide the series into four equal parts. There are only three quartiles. We denote them by Q₁, Q₂, and Q₃. Q₁ is called the lower quartile, which is the value such that (1/4)^th of the total observations fall below it and (3/4)^th above it. Q₂ is the same as median. Q₃ is called the upper quartile, which is the value such that (3/4)^th of the total observations fall below it and (1/4)^th above it. The method of determining quartiles is same as that of median.

STEPS

1. Arrange the data in ascending order
2. \( {\mathbf Q_1 = \Biggl[\frac {{N} + {1}}{4}}\Biggl]^{th} \) item
3. \( {\mathbf Q_1 = \Biggl[\frac {3({N} + {1})}{4}}\Biggl]^{th} \) item

DATA OF ODD NUMBERS

Find the first quartile Q₁, the median (Q₂) and the third quartile Q₃ of the following series.

12, 6, 21, 15, 9, 20, 16, 13, 8, 7, 9, 11, 5, 8, 10

Let us arrange the data in ascending order

5, 6, 7, 8, 8, 9, 9, 10, 11, 12, 13, 15, 16, 20, 21

Here N = 15

\( {\mathbf Q_1 = \Biggl[\frac {{N} + {1}}{4}}\Biggl]^{th} \) item

\( { = value\, of\, the\, \Biggl[\frac {{15} + {1}}{4}}\Biggl]^{th} \) item

= value of the 4^th item = 8.

\( {\mathbf Q_2 = \Biggl[\frac {{N} + {1}}{2}}\Biggl]^{th} \) item

\( { = value\, of\, the\, \Biggl[\frac {{15} + {1}}{2}}\Biggl]^{th} \) item

= value of the 8^th item = 10.

\( {\mathbf Q_3 = \Biggl[\frac {3({N} + {1})}{4}}\Biggl]^{th} \) item

\( { = value\, of\, the\, \Biggl[\frac {({15} + {1})}{4}}\Biggl]^{th} \) item

= value of the 12^th item = 15.

DATA OF EVEN NUMBERS

Find the first quartile Q₁, the median (Q₂) and the third quartile Q₃ of the following series.

166, 167, 171, 160, 133, 175, 156, 158, 175, 142, 120, 133

Let us arrange the data in ascending order

120, 133, 133, 142, 156, 158, 175, 166, 160, 167, 171, 175, 175

\( {\mathbf Q_1 = \Biggl[\frac {{N} + {1}}{4}}\Biggl]^{th} \) item

\( { = value\, of\, the\, \Biggl[\frac {{12} + {1}}{4}}\Biggl]^{th} \) item

= value of the 3.25^th item

= value of the 3^rd item + 0.25 (4^th item - 3^rd item)

= 133 + 0.25 (142 - 133)

= 133 + 0.25(9)

= 135.25.

\( {\mathbf Q_2 = \Biggl[\frac {{N} + {1}}{2}}\Biggl]^{th} \) item

\( { = value\, of\, the\, \Biggl[\frac {{12} + {1}}{2}}\Biggl]^{th} \) item

= value of the 6.5^th item

= value of the 6^th item + 0.5 (7^th item - 6^rd item)

= 158 + 0.5 (166 - 158)

= 158 + 0.5(8)

= 162.

\( {\mathbf Q_3 = \Biggl[\frac {3({N} + {1})}{4}}\Biggl]^{th} \) item

\( { = value\, of\, the\, \Biggl[\frac {({12} + {1})}{4}}\Biggl]^{th} \) item

= value of the 9.75^th item

= value of the 9^th item + 0.75 (10^th item - 9^th item)

= 167 + 0.75 (171 - 167)

= 167 + 0.75(4)

= 170.

STEPS

1. Arrange the data in ascending order
2. Find the cumulative frequencies
3. \( \mathbf {Q_1 = \Biggl[\frac {{N} + {1}}{4}}\Biggl]^{th} \) item
4. \( \mathbf {Q_3 = \Biggl[\frac {3({N} + {1})}{4}}\Biggl]^{th} \) item

Let us find the first quartile Q₁, the median (Q₂) and the third quartile Q₃ of the following series.

Values	Frequencies
5	8
8	13
12	20
15	22
17	11
20	6

Here N = 80,

\( \mathbf {Q_1 = \Biggl[\frac {{N} + {1}}{4}}\Biggl]^{th} \) = 20.25

\( \mathbf {Q_2 = \Biggl[\frac {{N} + {1}}{2}}\Biggl]^{th} \) = 40.5

\( \mathbf {Q_3 = \Biggl[\frac {3({N} + {1})}{4}}\Biggl]^{th} \) = 60.75

Now we can create a table showing cumulative frequencies

Values	Frequencies	cf
5	8	8
8	13	21 (Q1 lies here)
12	20	41 (Q2 lies here)
15	22	63 (Q3 lies here)
17	11	74
20	6	80
	N = 80

\( \mathbf {Q_1 = \Biggl[\frac {{N} + {1}}{4}}\Biggl]^{th} \) item

= value of the 21^st item = 8

\( \mathbf {Q_2 = \Biggl[\frac {{N} + {1}}{2}}\Biggl]^{th} \) item

= value of the 41^st item = 12

\( \mathbf {Q_3 = \Biggl[\frac {3({N} + {1})}{4}}\Biggl]^{th} \) item

= value of the 61^st item = 15

STEPS

1. Find the cumulative frequency
2. Find Q₁ and Q_{3 classes}
3. \( { \mathbf Q_1 =\, size\, of\,\frac {{N}}{4}}^{th} \) item
4. \( { \mathbf Q_3 =\, size\, of\,\frac {3{N}}{4}}^{th} \) item

After locating these classes, the values of Q₁ and Q₃ can be interpolated.

$$ \mathbf Q_1 \,= \,{ L + \frac{\frac{N}{4} - {cf}}{f} × h} $$

Where,

L = the lower limit of the lower quartile class

f = freqwuency of the lower quartile class

h = magnitude of the lower quartile class

cf = the cumulative frequency of the class preceding the lower quartile class $$ \mathbf Q_3 \,= \,{ L + \frac{\frac{3N}{4} - {cf}}{f} × h} $$

Where,

L = the lower limit of the upper quartile class

f = freqwuency of the upper quartile class

h = magnitude of the upper quartile class

cf = the cumulative frequency of the class preceding the upper quartile class

Let us find the first quartile Q₁, the median (Q₂) and the third quartile Q₃ of the following series.

Age	Frequencies
0-5	2
5-10	5
10-15	9
15-20	13
20-25	18
25-30	24
30-35	19
35-40	17
40-45	10
45-50	3

We can create a table with cumulative frequency to find Q₁, Q₂, and Q₃.

Age	Frequencies	cf
0-5	2	2
5-10	5	7
10-15	9	16
15-20	13	29
20-25	18	47
25-30	24	71
30-35	19	90
35-40	17	107
40-45	10	117
45-50	3	120
	N = 120

N = 120, \( { \frac {{N}}{4}} \) = 30

Lower Quartile Class = 20 - 25

L = 20, \( {\frac {{N}}{4}} \) = 30, cf = 29, f = 18, h = 5

\( \mathbf Q_1 \,= \,{ L + \frac{\frac{N}{4} - {cf}}{f} × h} \)

= \( { 20 + \frac{{30} - {29}}{18} × 5} \)

= 20.28

N = 120, \( { \frac {{N}}{2}} \) = 60

Median Class = 25 - 30

L = 25, \( {\frac {{N}}{2}} \) = 60, cf = 47, f = 24, h = 5

\( \mathbf Q_2 \,= \,{ L + \frac{\frac{N}{2} - {cf}}{f} × h} \)

= \( { 25 + \frac{{60} - {47}}{24} × 5} \)

= 27.7

N = 120, \( { \frac {3{N}}{4}} \) = 90

Upper Quartile Class = 30 - 35

L = 30, \( {\frac {3{N}}{4}} \) = 90, cf = 71, f = 19, h = 5

\( \mathbf Q_3 \,= \,{ L + \frac{\frac{3{N}}{4} - {cf}}{f} × h} \)

= \( { 30 + \frac{{90} - {71}}{19} × 5} \)

= 35