
Price Elasticity of Demand
In Economics elasticity in very important. It was Alfred Marshal who first used the concept of elasticity in Economics. Price Elasticity can determine the amount of change in demand brought about by price changes. The word elasticity means responsiveness. Price elasticity of demand may be defined as the degree of responsiveness of quantity demanded of a commodity in response to change in its price.Price elasticity of demand is determined by the degree of change in quantity demanded in response to change in its price. On dividing the percentage of the change in demand by the percentage of change in price we get price elasticity.
Degree of Price Elasticity Elasticity will be different for different commodities. On the basis of rate of change in the quantity demanded, elasticity can be divided into five:
1. Elastic Demand (e > 1)
If the percentage of change of demand is greater than the percentage of change in price, it is called elastic demand. For example, when price changes by 10% demand increases by 30%. When elasticity of demand is high, the absolute value of elasticity will be more than one.
i.e. (│e│ > 1 or e < -1).
In the above example,
\( \vert e \vert \,=\,{\frac{30%}{10%}}\,=\,3. \)
Then Demand curve will be more flat as shown in the below diagram. Or the slope will be less.
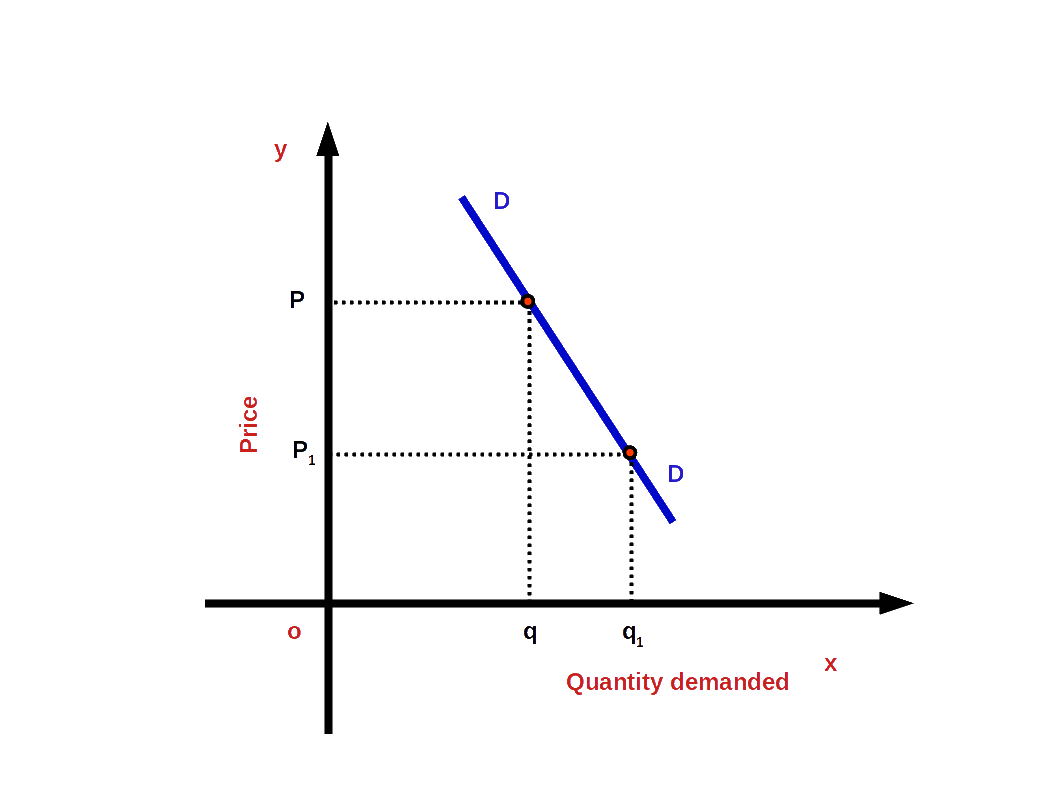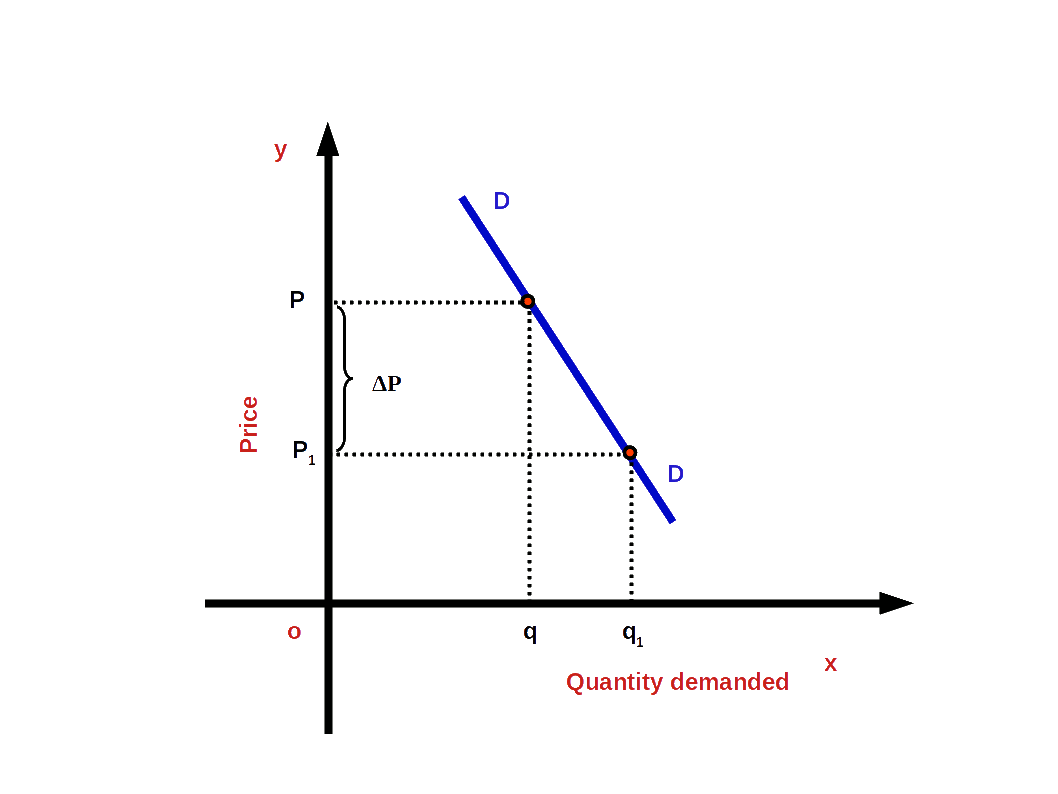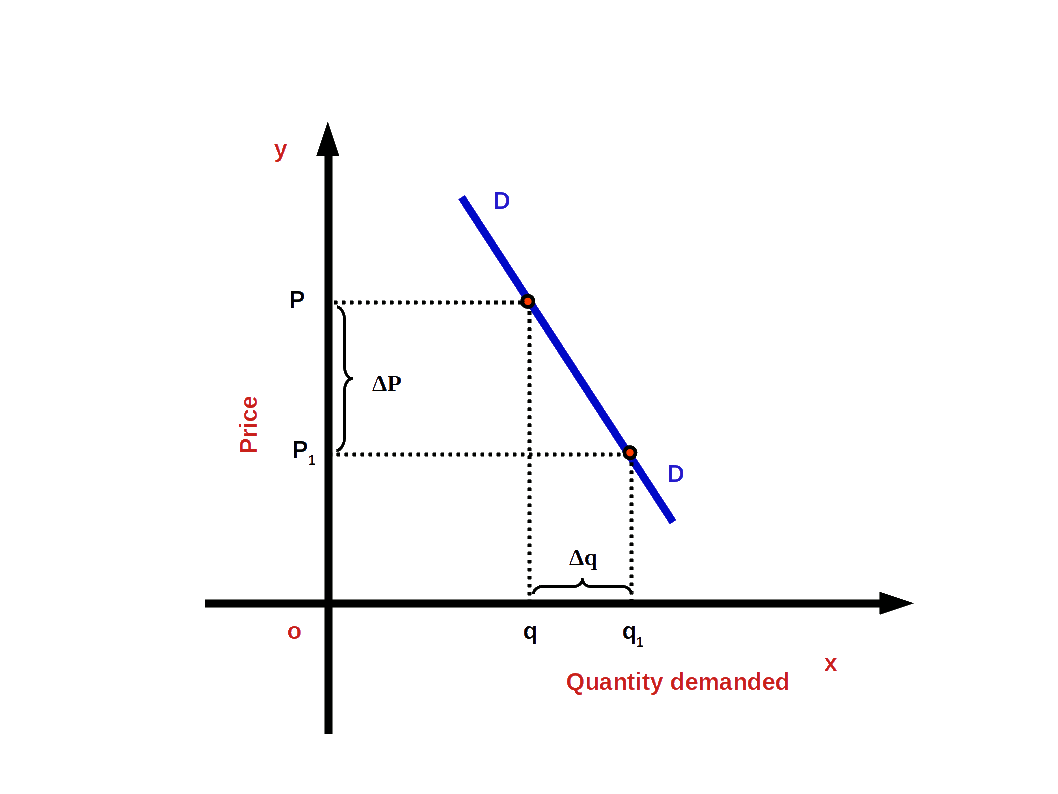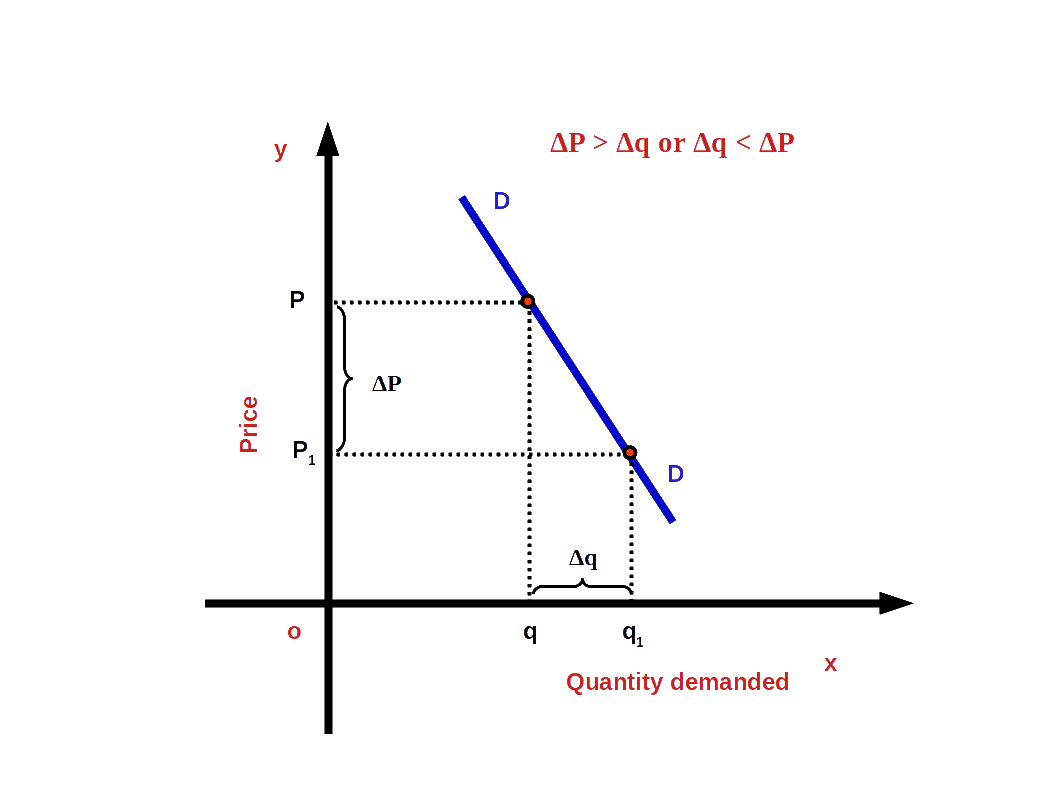
2. Inelastic Demand (e < 1)
If the percentage change in demand is less than the percentage change in price, it is called inelastic demand or less elastic demand, For example, when percentage change in Price is 20% and change in demand is only 10%. In inelastic demand the absolute value of elasticity would be less than one.
i.e. (│e│ < 1 or e > -1)
In the above example,
\( \vert e \vert \,=\,{\frac{10%}{20%}}\,=\,0.5. \)
In this case demand curve would be less flat or more steep as shown in the blow Diagram.
3. Unitary Elastic Demand (e = 1)
If the percentage change in demand and percentage change in price are equal, it is called unitary elastic demand. For example, when there is 10% change in price it results in 10% change in demand.
Under unitary elastic demand, the absolute value of elasticity will be one.
i.e. (│e│ = 1 or e = -1)
In the above example,
\( \vert e \vert \,=\,{\frac{10%}{10%}}\,=\,1. \)
Then the demand curve would have a moderate slope as shown in the below given diagram.
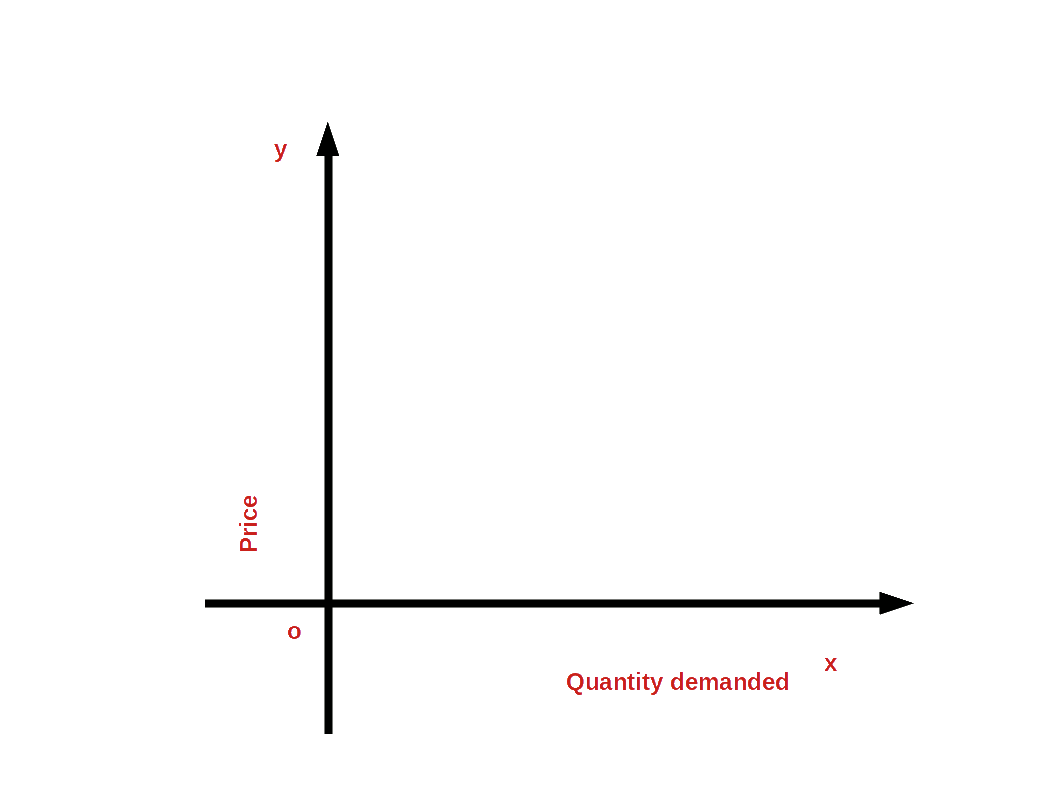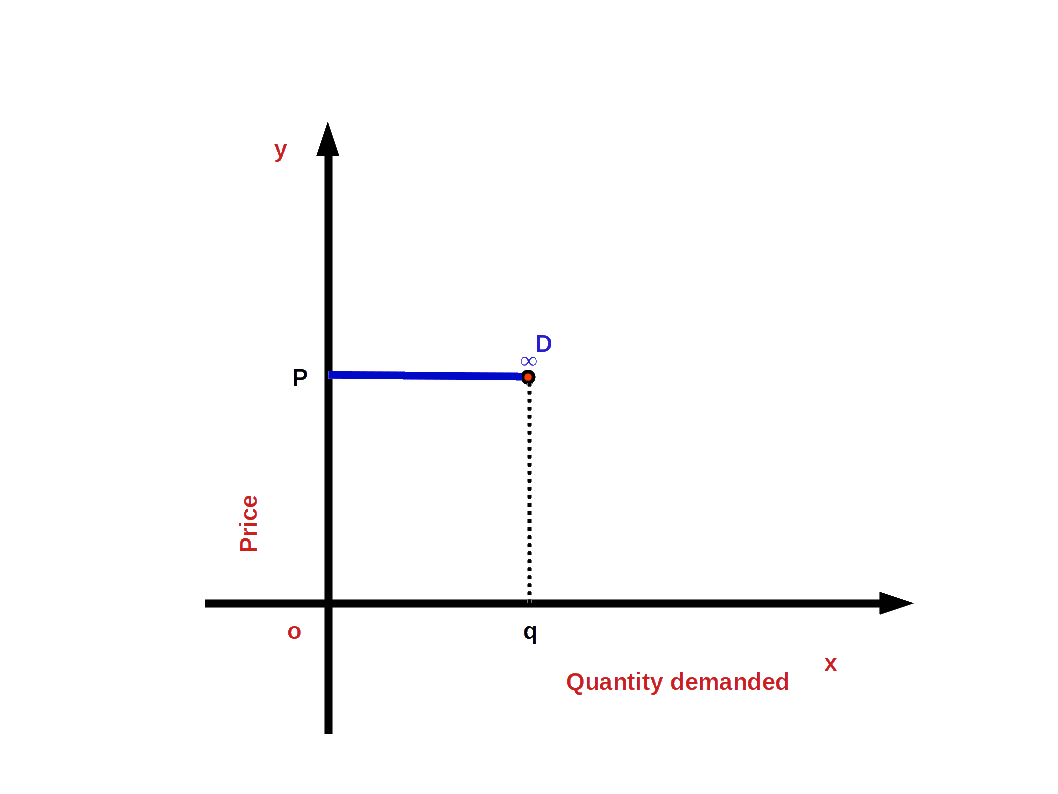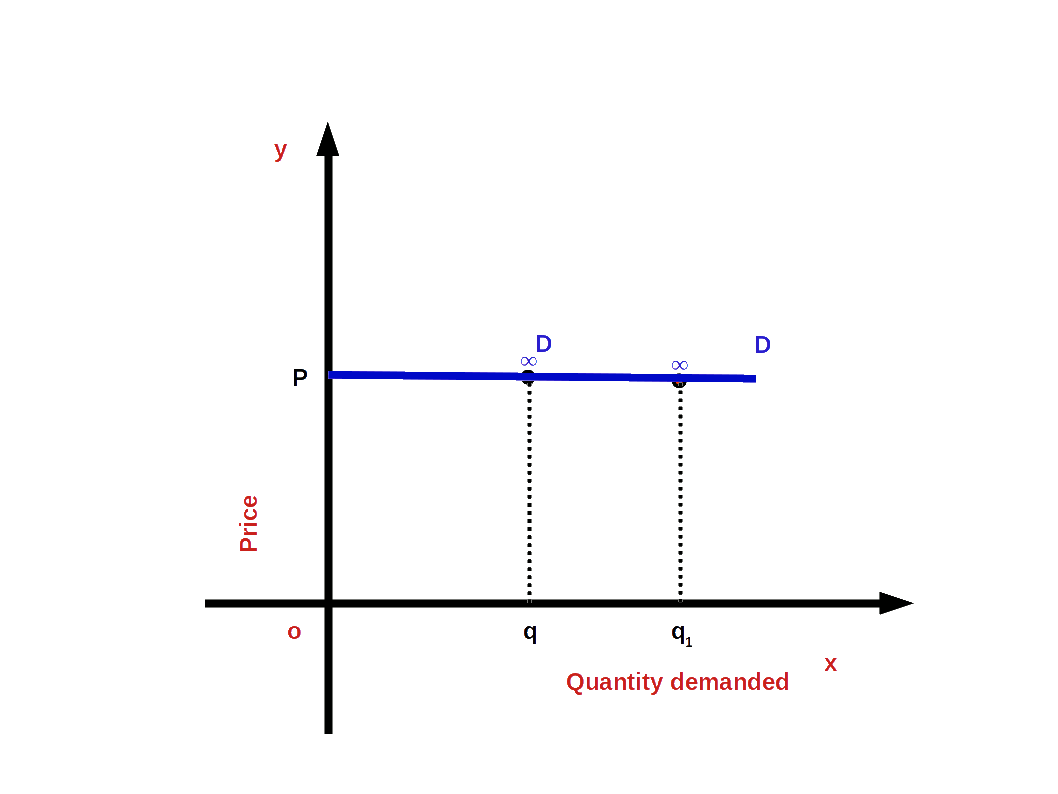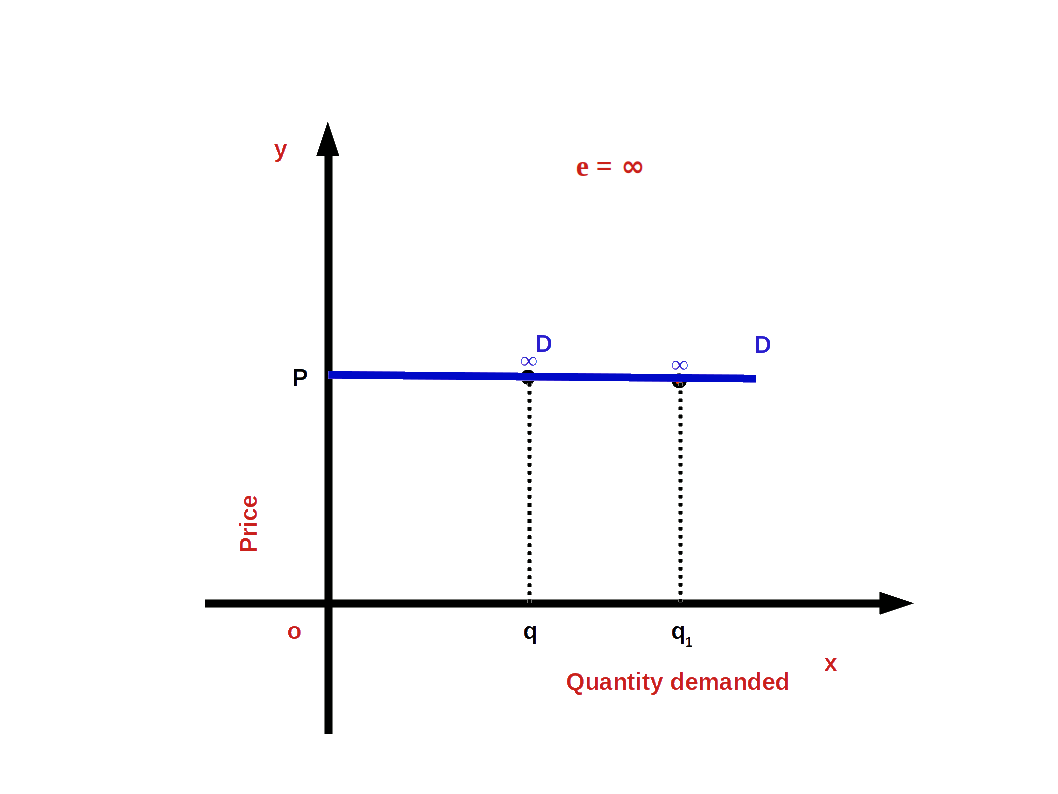
4. Perfectly Elastic Demand (e = ∞)
When a small change in price leads to infinite change in demand, we have perfectly elastic demand. In such cases, the absolute value of elasticity would be infinite or unlimited.
i.e. (│e│ = ∞ or e = -∞)
and the demand curve would be parallel to x-axis or horizontal as shown in the below Diagram. The slope of demand curve would be 0.
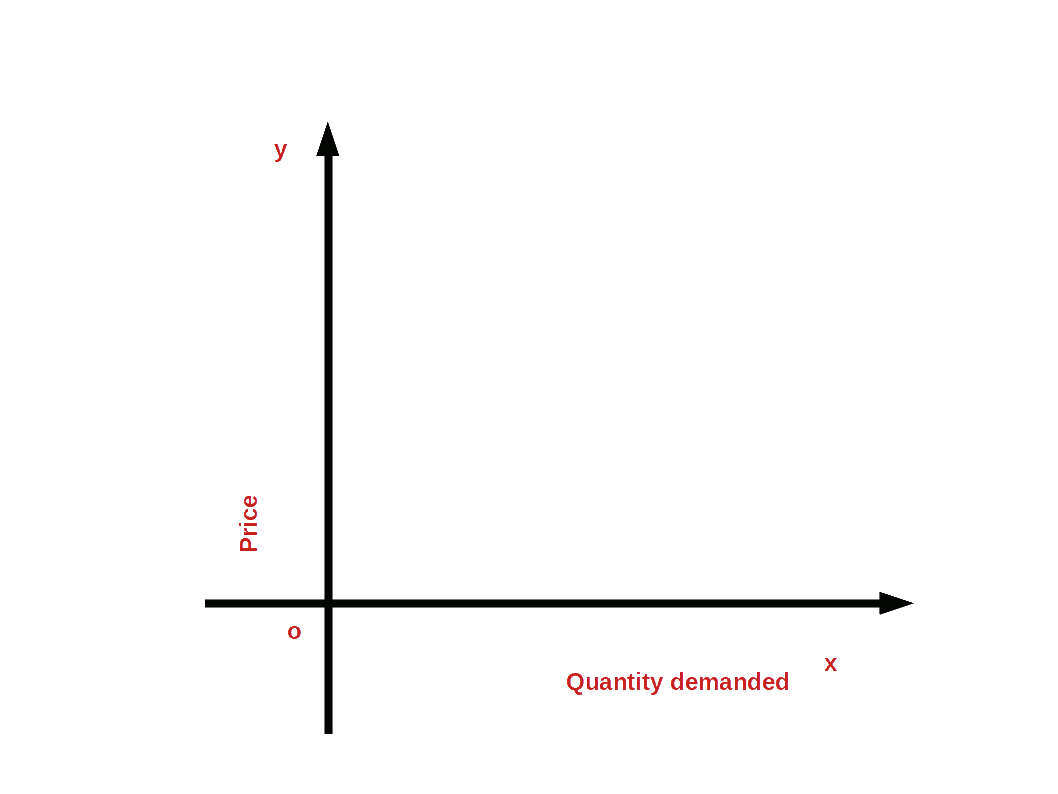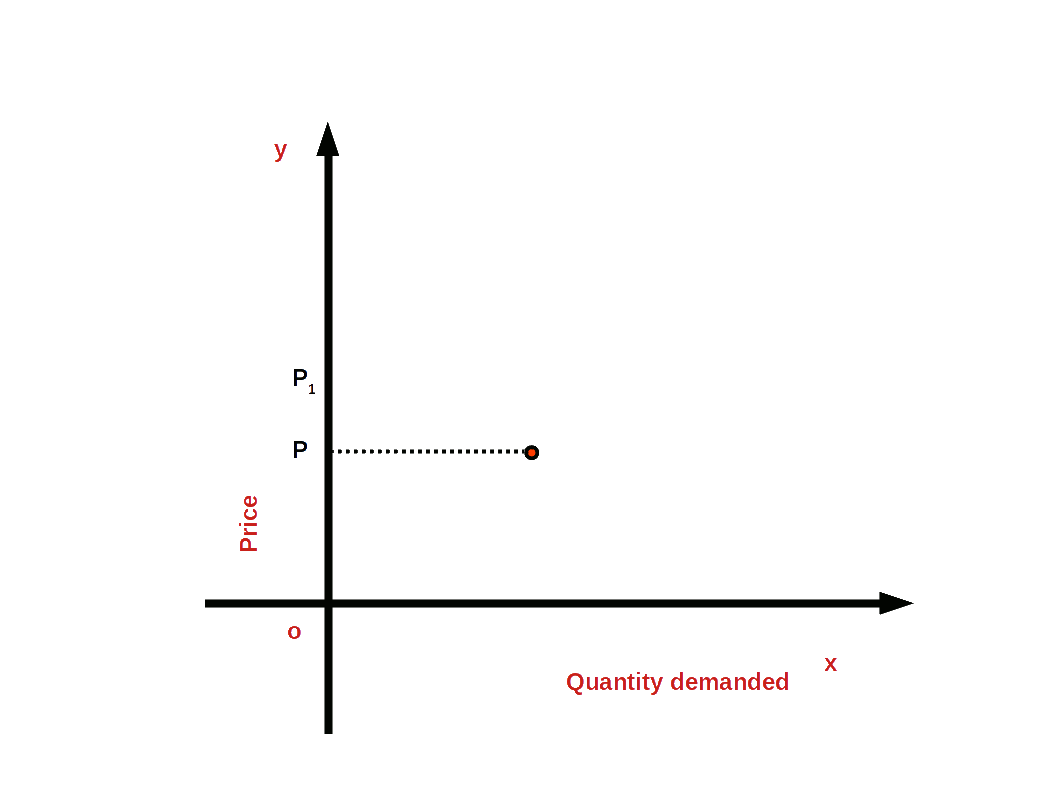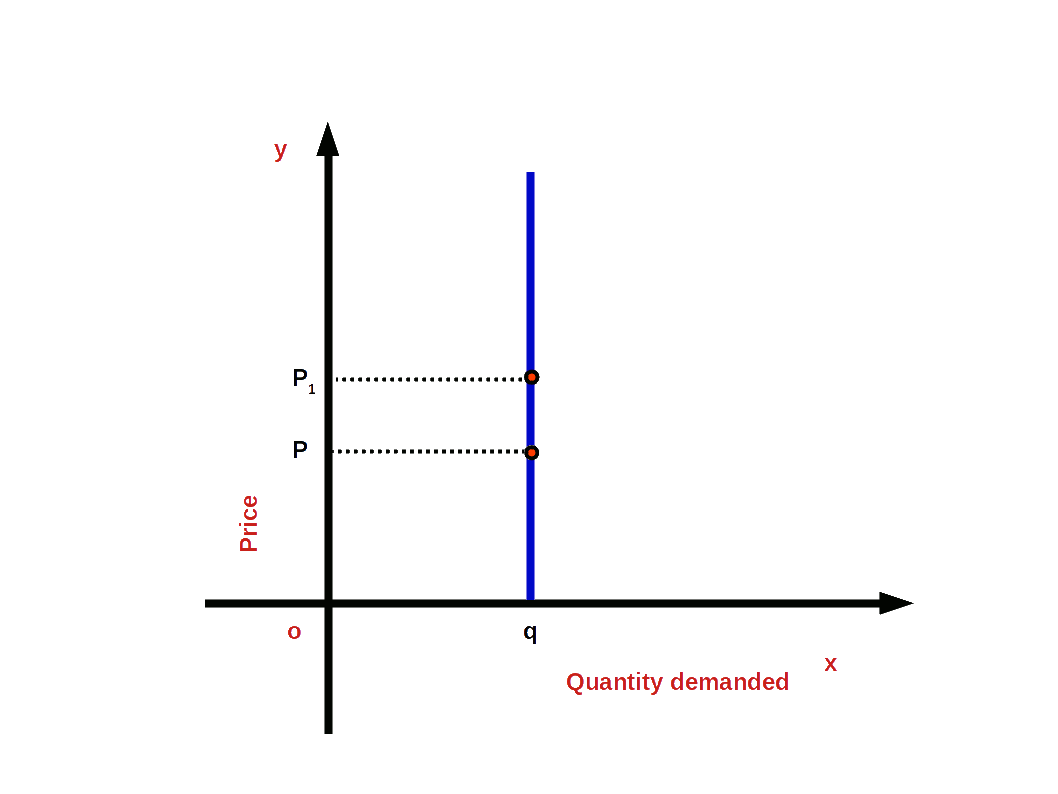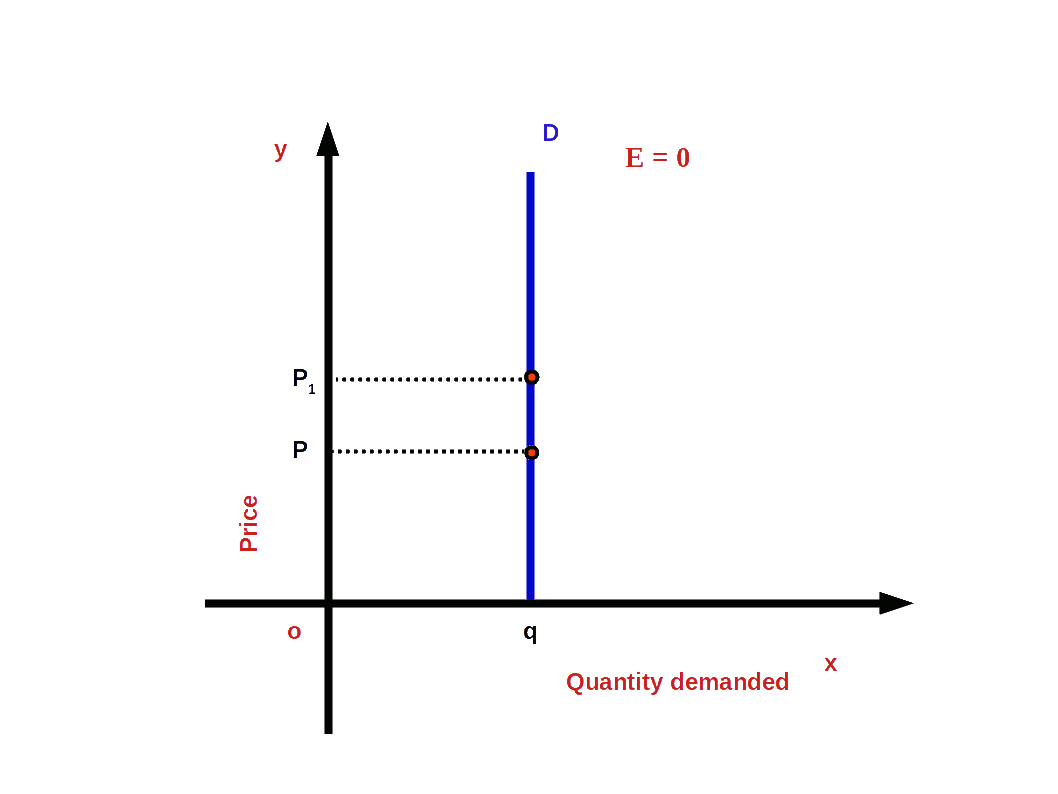
5. Perfectly Inelastic Demand (e = 0)
Perfectly inelastic demand is a situation in which, whatever may be the changes in price, quantity demanded is un-affected. In this case the value of elasticity would be 0. Then demand curve would be
vertical to x - axis as shown in the below Diagram.
i.e. (│e│ = 0 or e = 0)
Among the five degrees of elasticity of demand, perfectly elastic demand and perfectly inelastic demand are rare in practical life.
Methods of measuring Price Elasticity of Demand
Price elasticity is measured in three different ways:
(1) Percentage method
(2) Measurement of elasticity along a linear demand curve
(3) Expenditure method
(1) Percentage method
Under percentage method price elasticity of demand is measured by dividing the percentage change in quantity demanded by the percentage change in price.
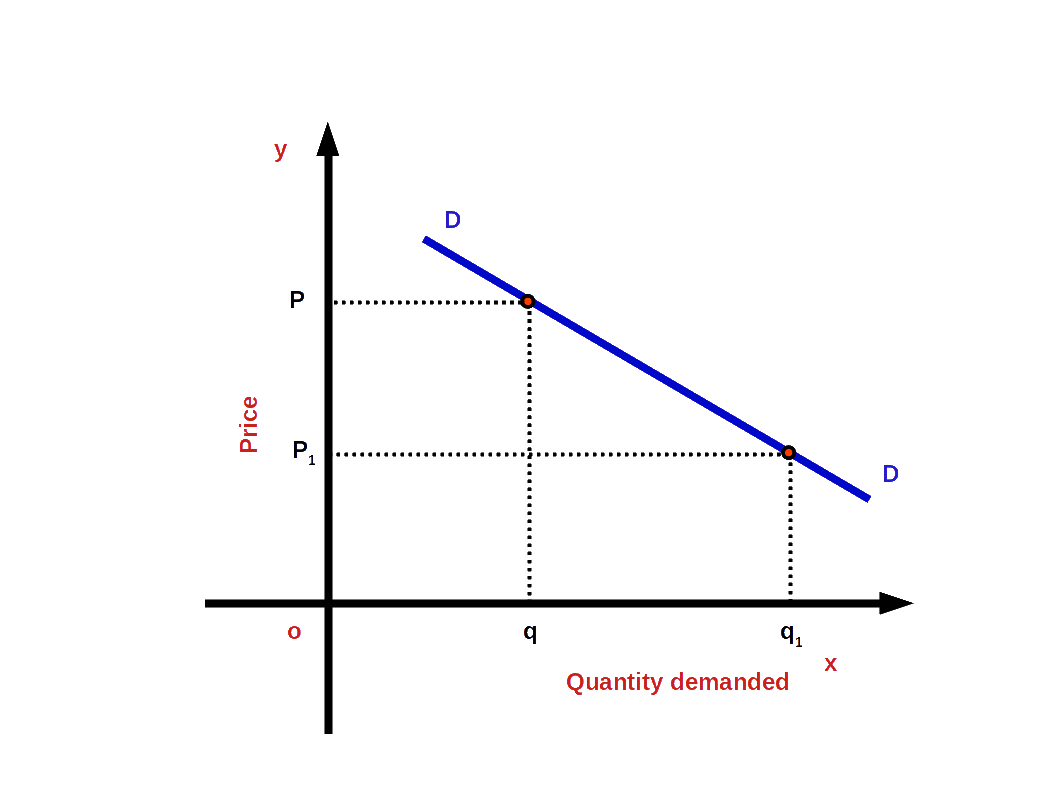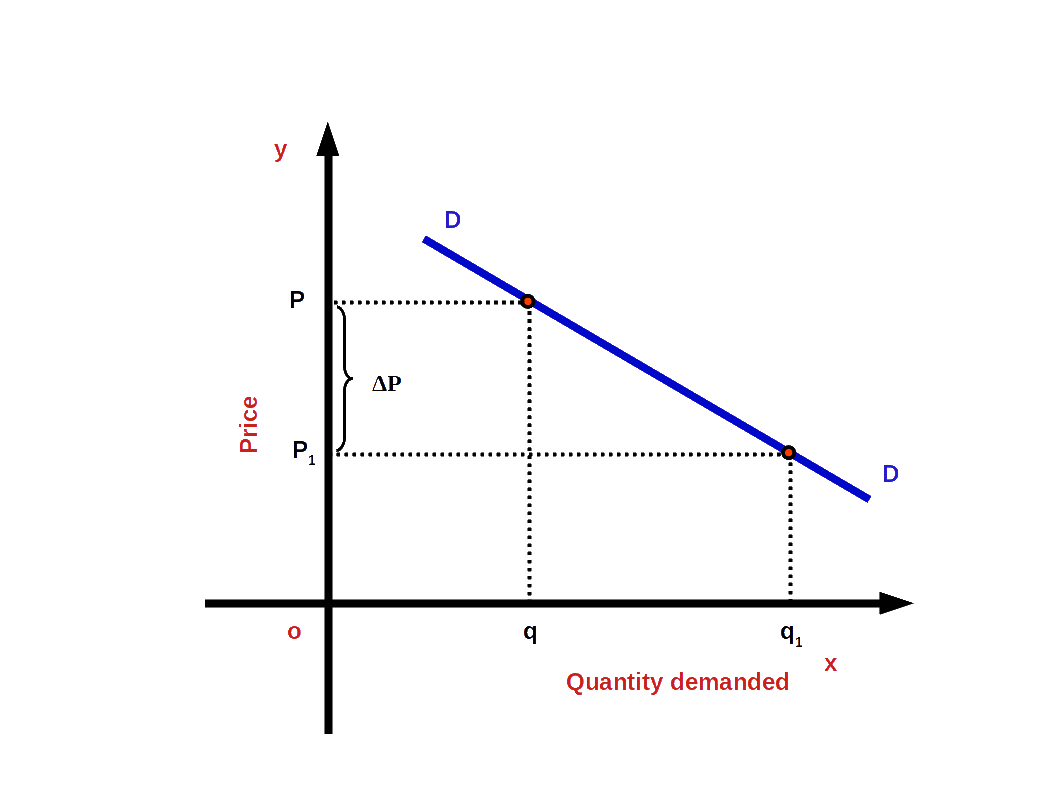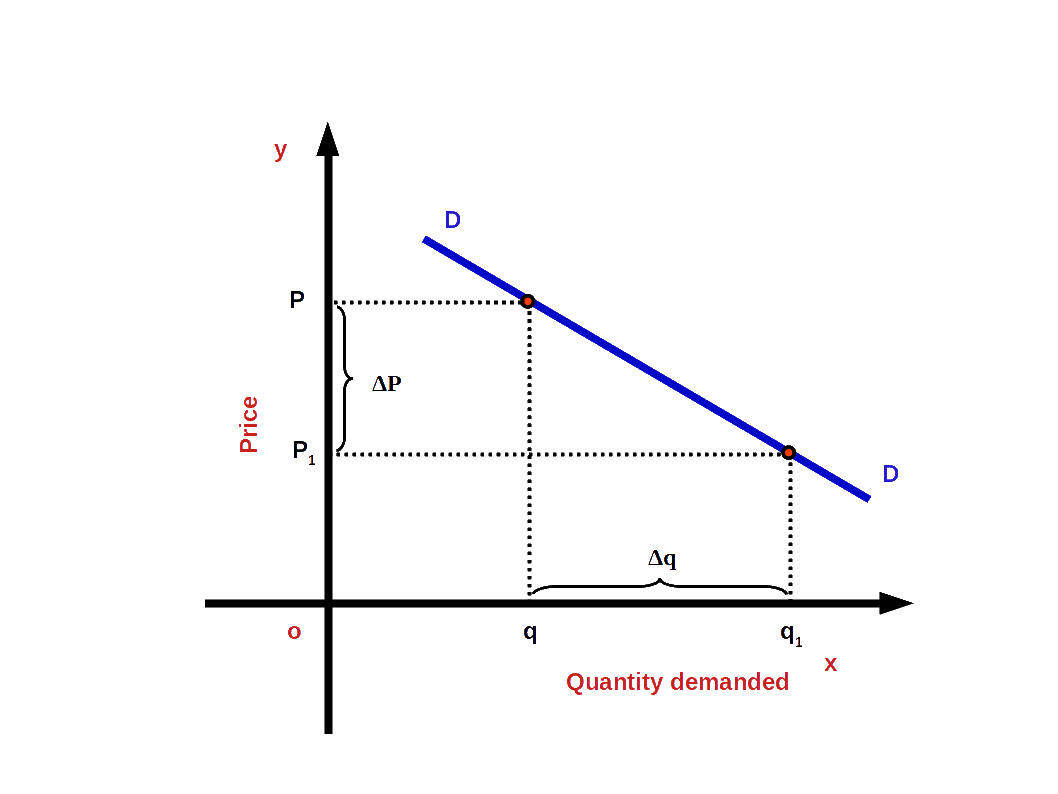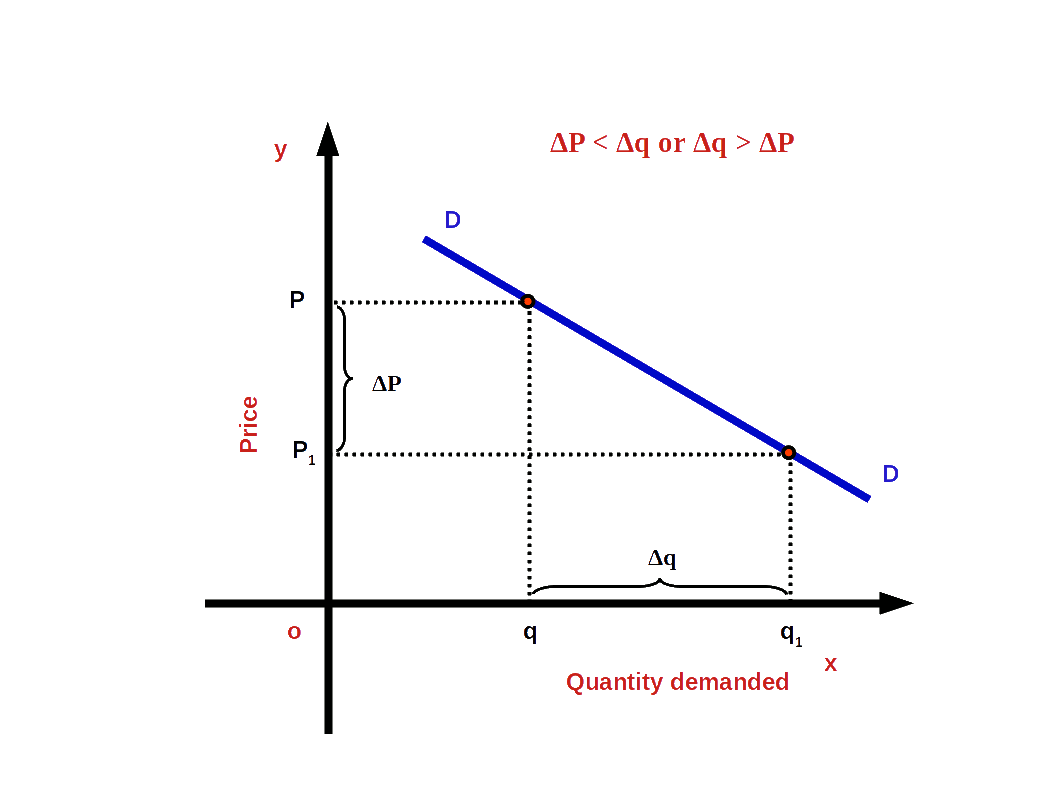
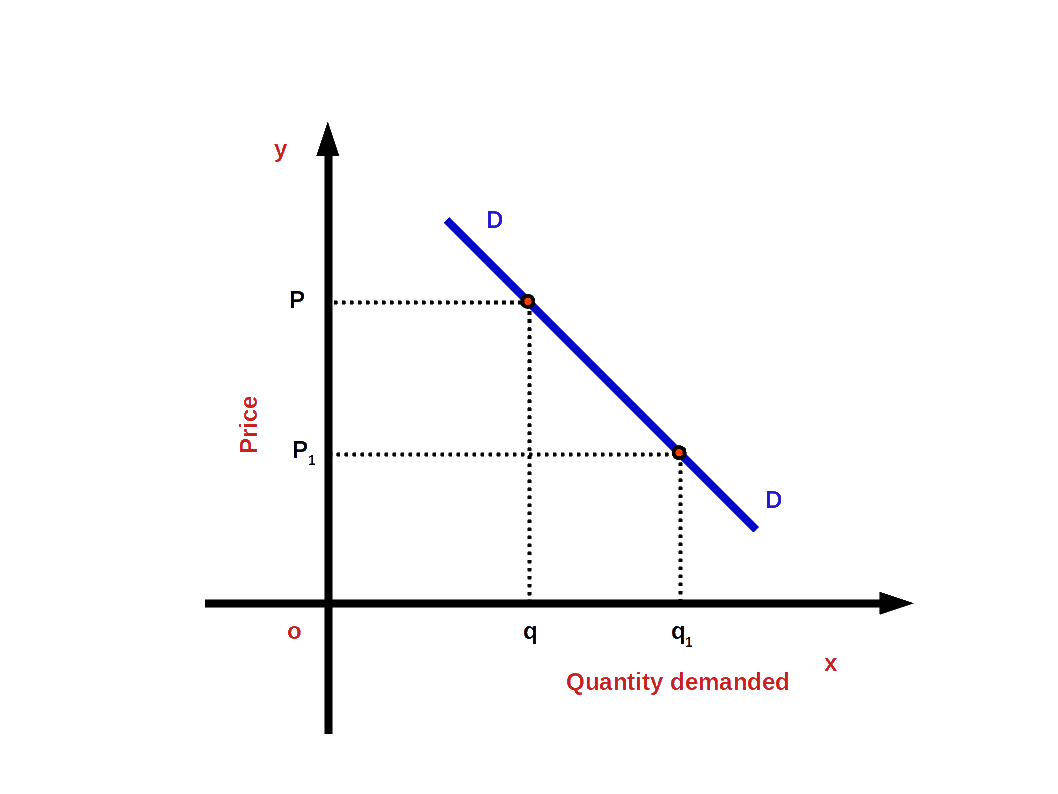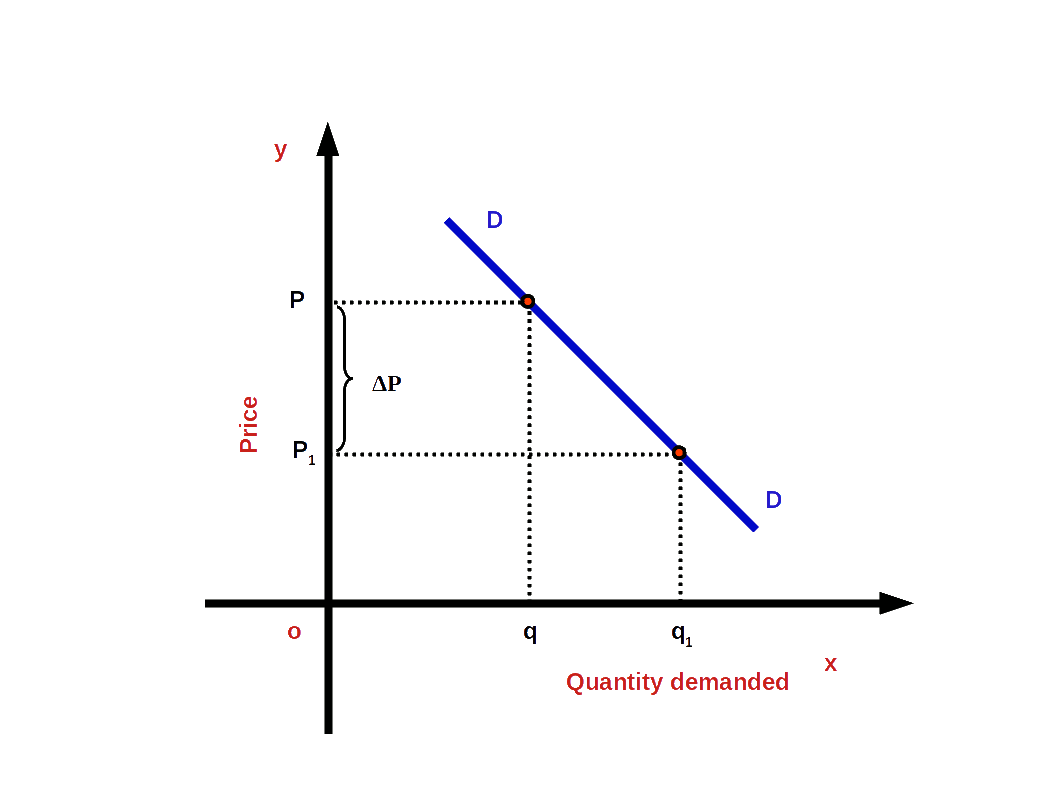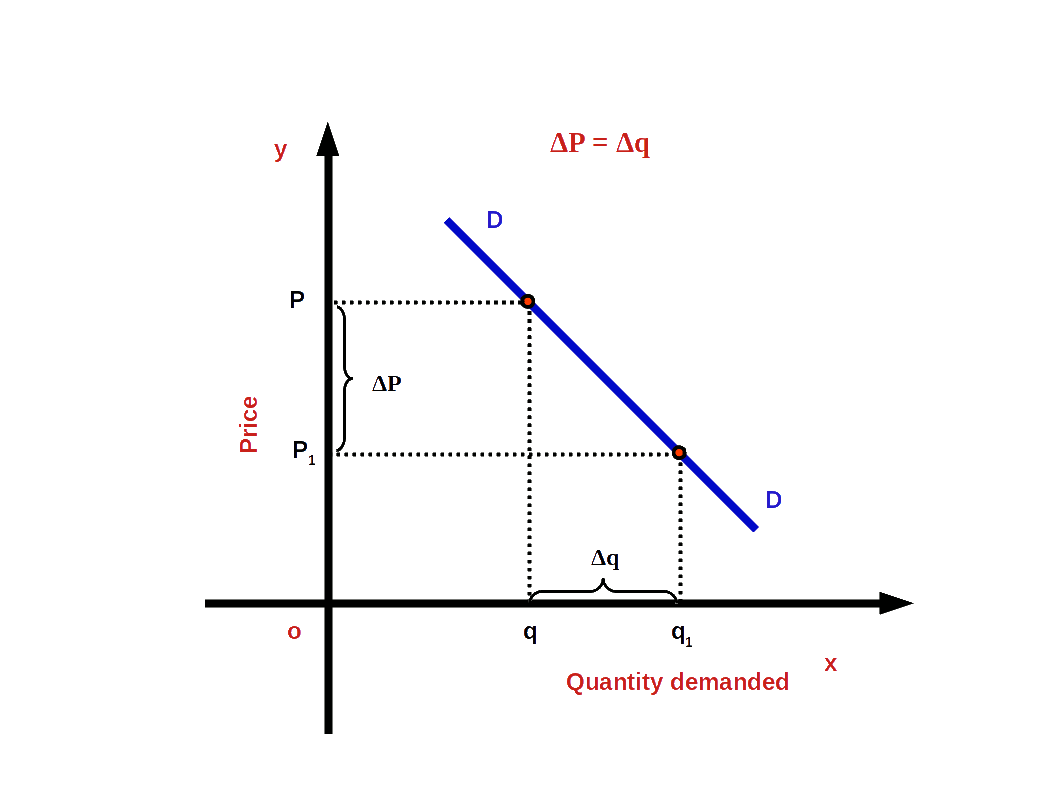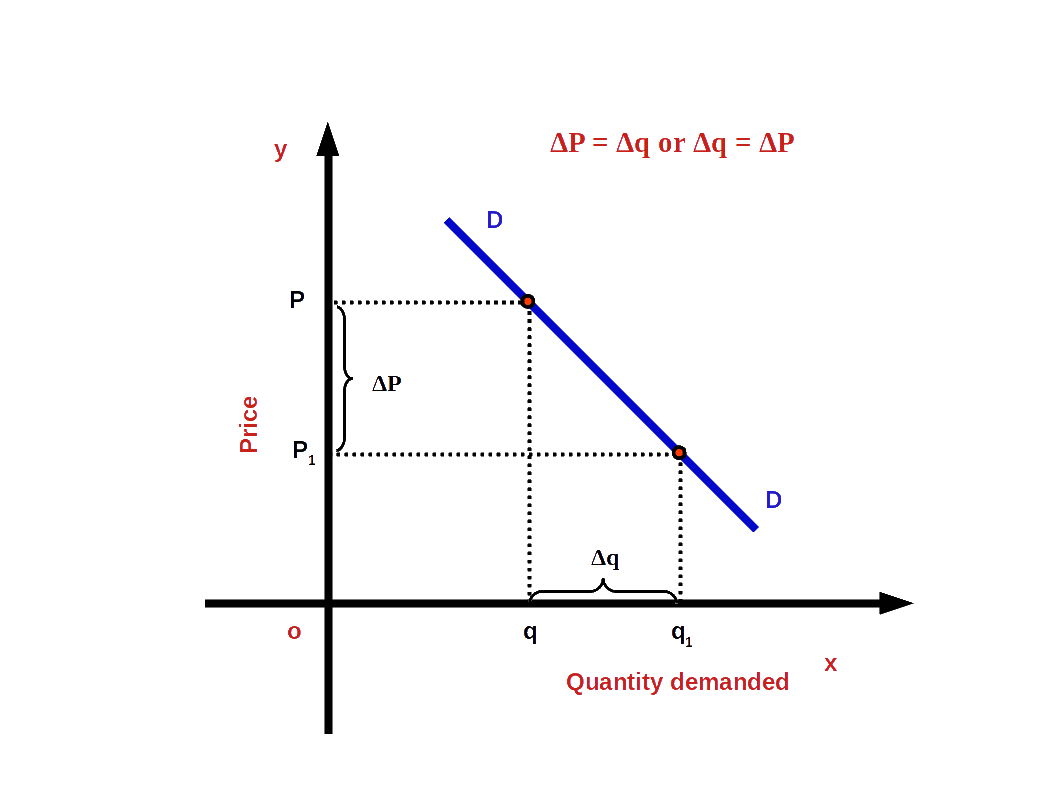
Price elsticity of demand = $$ \mathbf {{\frac{Percentage\,change\,in\,quantity\,demanded}{Percentage\,change\,in\,price}}} $$ $$ \mathbf {e \,=\,{\frac{{\frac{Change\, in\, quantity}{Initial\, quantity}}× 100}{{\frac{Change\, in\, price}{Initial\, price}}× 100}}} $$If P = initial price, q = initial quantity demanded, ΔP.= change in price and Δq = change in quantity demanded then,
$$ \mathbf {e \,=\,{\frac{{\frac{Δq}{q}}× 100}{{\frac{ΔP}{P}}× 100}}} $$
$$ \mathbf {e \,=\,{{{{\frac{Δq}{q}}}}÷{{{\frac{ΔP}{P}}}}}} $$
$$ \mathbf {e \,=\,{{{{\frac{Δq}{ΔP}}}}×{{{\frac{P}{q}}}}}} $$
Since the price of good is measured in rupees and quantity demanded is measured in units like kilograms, the value of elasticity will be a pure unitless number. Similarly, since price and quantity move in opposite directions the value of elasticity would be a negative number. But the absolute value of price elasticity is usually used.
p = ₹ 60, ΔP = ₹ 10, q = 100 litres, and Δq = 20.
Price elasticity of petrol \( \mathbf {e \,=\,{{{{\frac{Δq}{ΔP}}}}×{{{\frac{P}{q}}}}}} \)
\( {=\,{{{{\frac{20}{10}}}}×{{{\frac{60}{100}}}}}} \)
\( {=\,{{{{\frac{1200}{1000}}}}}} =\, 1.2\)
Since e >1 it is high elasticity demand.
(2) Measurement of elasticity along a linear demand curve
Elasticity of each point on a linear demand curve would be different. Consider the linear demand curve q = a - bp. Change in price by one unit brings about a change in demand \( { \,=\,{{{{\frac{Δq}{ΔP}}}}}} \) = -b. since
\( {e \,=\,{{{{\frac{Δq}{ΔP}}}}×{{{\frac{P}{q}}}}}} \) \( { \,=\,{{{{\frac{-bP}{q}}}}}} \) \( \biggl({ Since\,{{{{\frac{Δq}{ΔP}}}}}} =\, -b \biggr) \)
\( {e\,=\,{\frac{-bP}{a\,-\,bP}}} \) Since q = a - bP

The value of elasticity changes with the change in P and q.
\( {e\,=\,{\frac{-bP}{a\,-\,bP}}} \) (-b = 2, a = 20, P = 5)
\( {e\,=\,{\frac{-2×5}{20\,-\,2×5}}} \)
\( {e\,=\,{\frac{-10}{20\,-\,10}}} \)
\( {e\,=\,{\frac{-10}{10}}} \) = -1 │e│ = 1
Geometric measure of elasticity
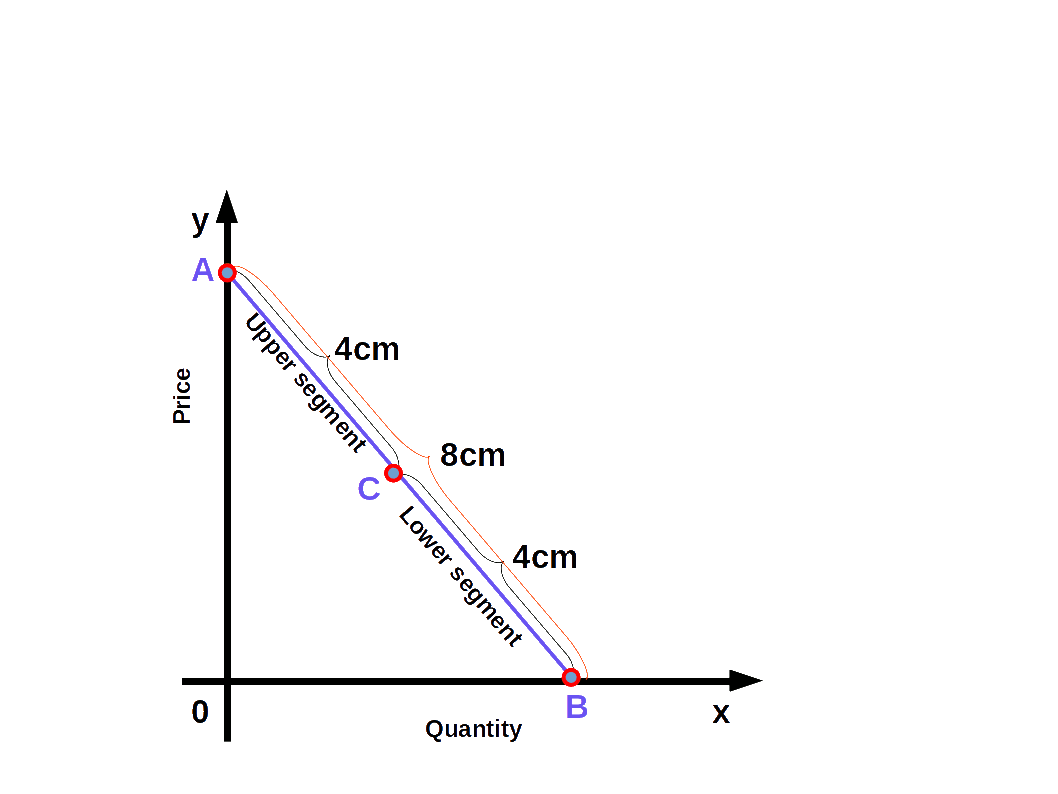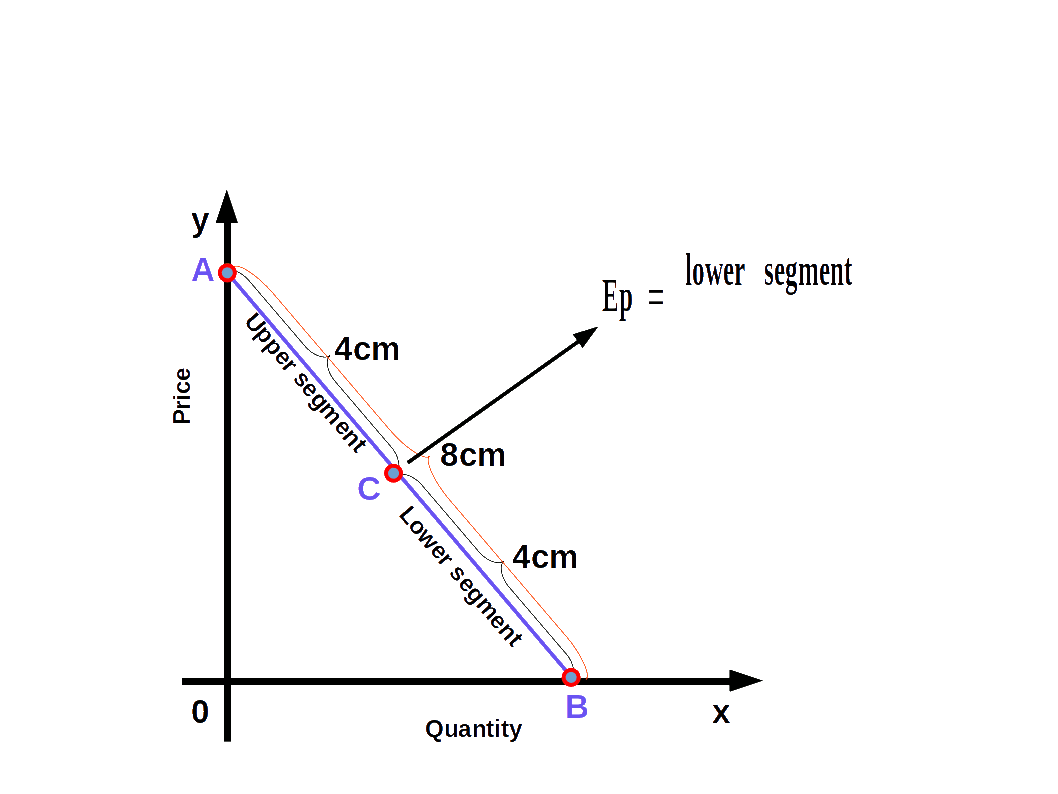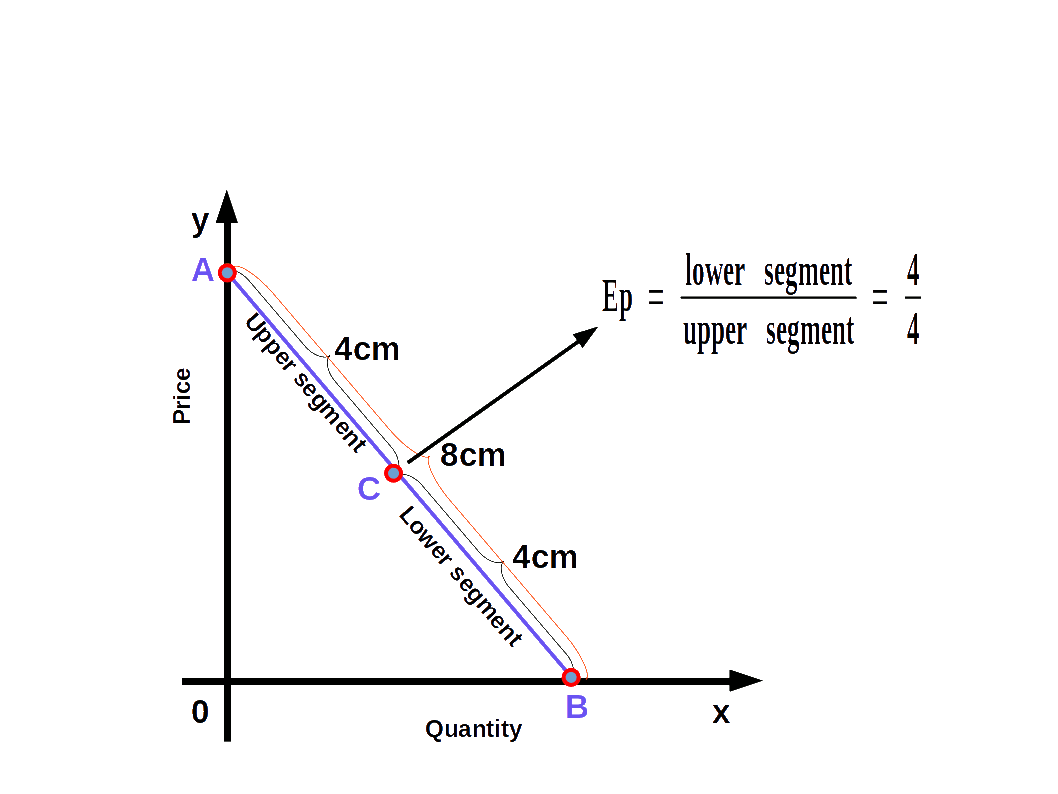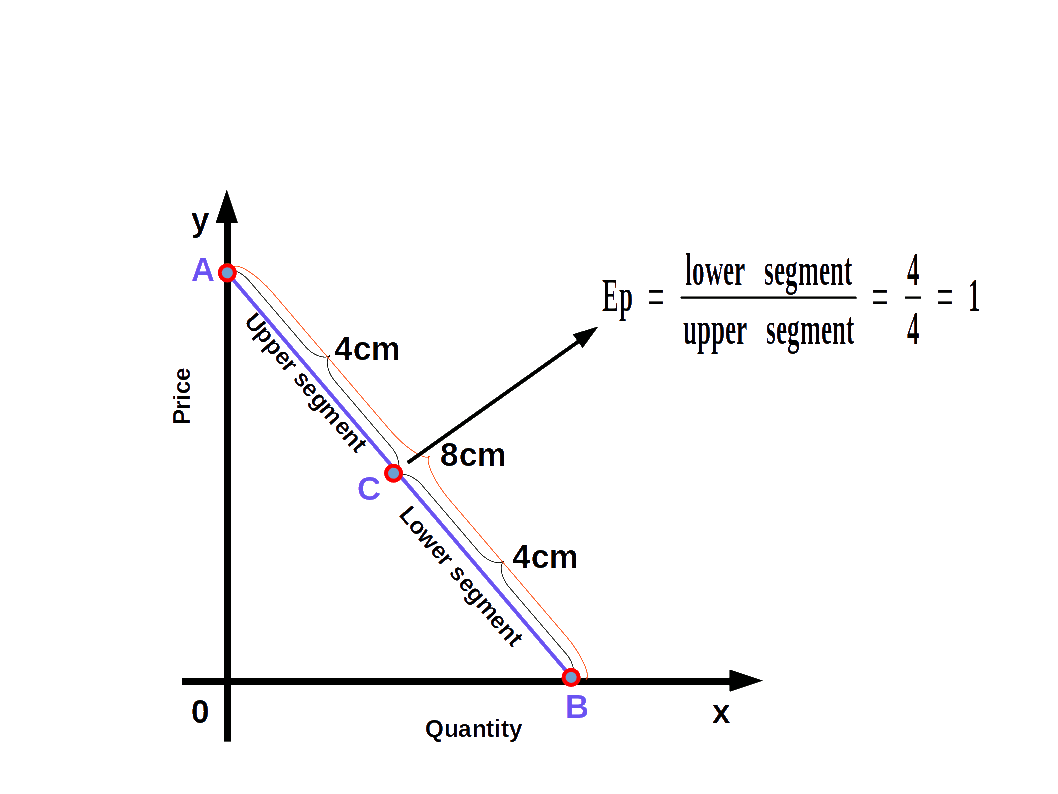
We can easily find out the elasticity of different points on a linear demand curve that touches at x- axis and y-axis- by using the geometric method. In this method we divide the lower segment of the linear demand curve with the upper segment.
$$ {\mathbf{e\,=\,{\frac{lower\, segment}{upper\, segment}}}} $$
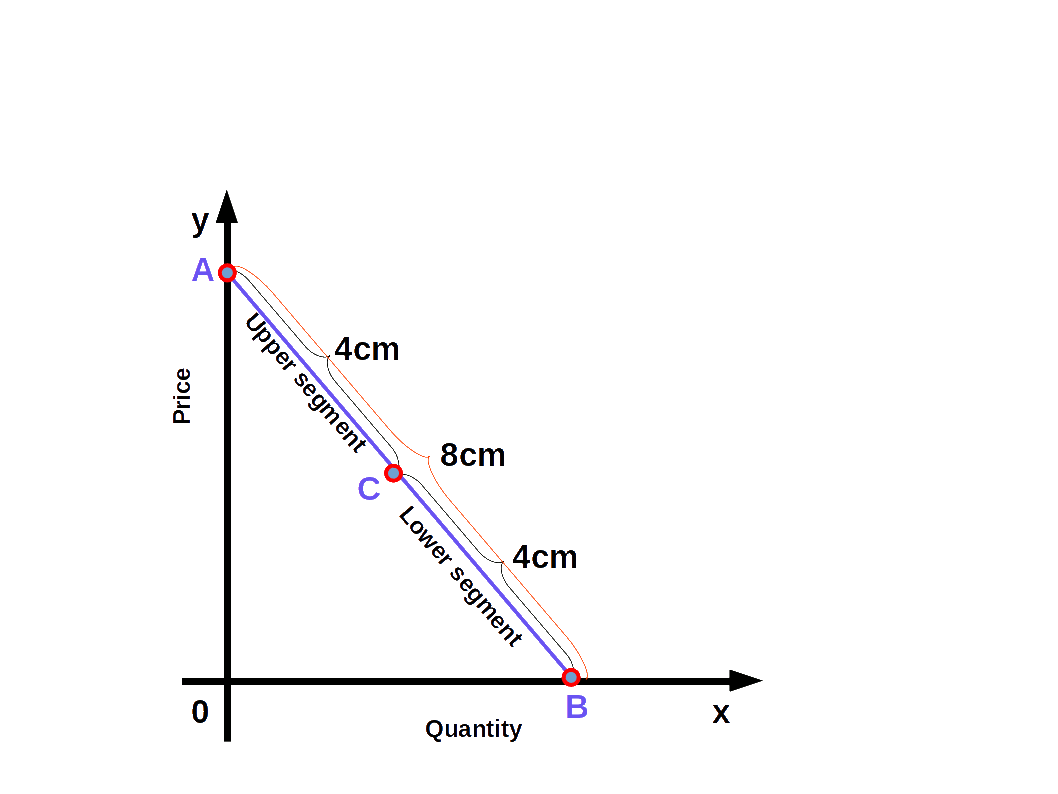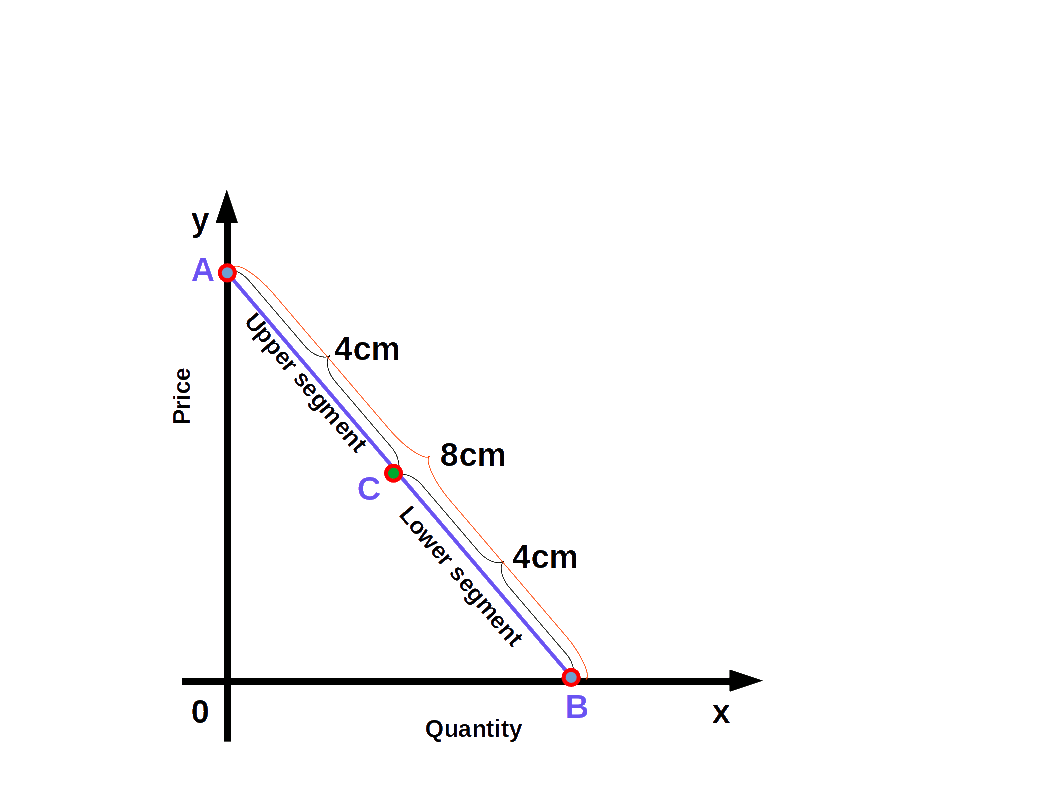
In the above Diagram, C is a point on the demand curve AB. The length of the lower segment, CB is 4cm and that of the upper segment AC is also 4cm. Therefore,
$$ {{e\,=\,{\frac{lower\, segment}{upper\, segment}}}} $$
$$ {{=\,{\frac{4}{4}}}} = 1 $$
We get price elasticity of demand as 1.
3. Expenditure method
The expenditure is calculated by multiplying price and quantity demanded, i.e., E = pq. Under expenditure method the elasticity is determined by comparing the change in price and the change in expenditure. In this method we can find whether elasticity is more than one, unitary, or less than one.
- If price and expenditure move in the opposite direction, elasticity will be more than one. When price increases expenditure decreases, and when price decreases, expenditure increases.
- When price changes and expenditure remains unchanged, elasticity will be one or unitary. i.e., there is no change in expenditure though price changes.
- If price and expenditure move in the same direction elasticity will be less than one. i.e., when price rises, expenditure also rises, and when the price falls, expenditure also falls. The relation between price; expenditure and elasticity is given in below Table.
| Table 2.1 Expenditure Method | |||
| Price | Quantity | Expenditure | Elasticity |
|---|---|---|---|
| 10 | 5 | 50 | e > 1 |
| 15 | 3 | 45 | |
| 10 | 6 | 60 | e = 1 |
| 15 | 4 | 60 | |
| 10 | 7 | 70 | e < 1 |
| 15 | 6 | 90 | |
Constant Elasticity Demand Curve
Elasticity of a linear demand curve can be any value from 0 to ~. But in some demand curves elasticity will be constant at all points. Whatever may be the changes in price, quantity demanded is unaffected is called constant elasticity of demand.
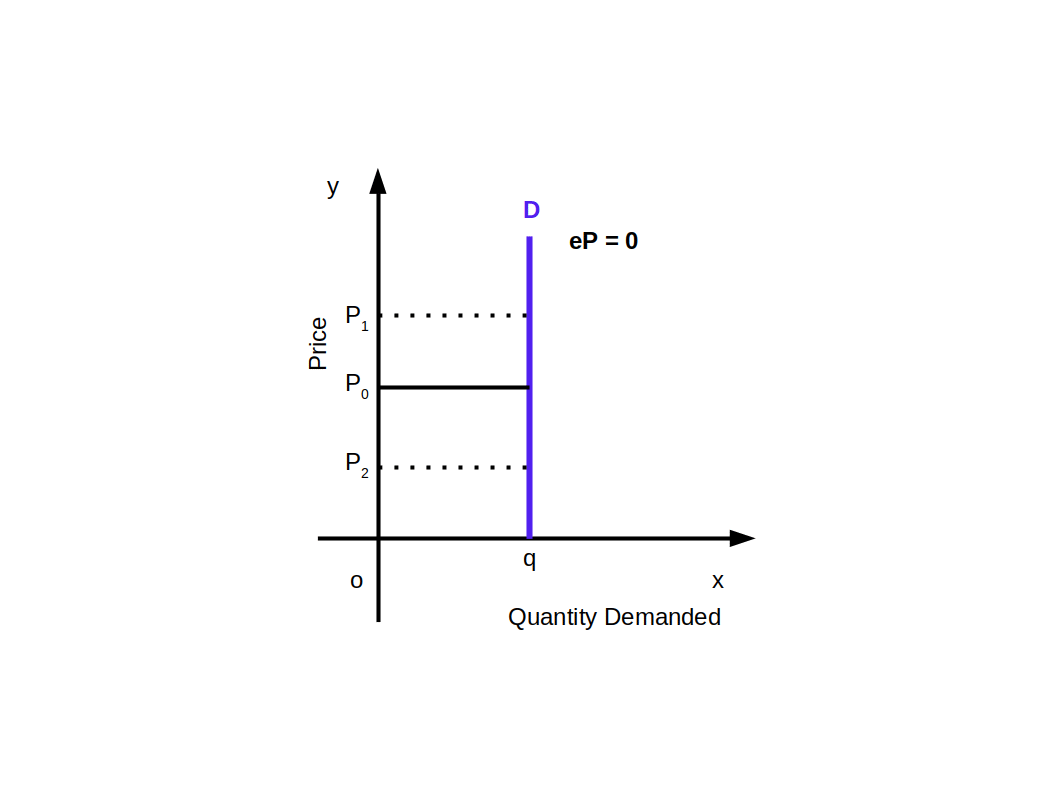
Above given Diagram shows a vertical demand curve that indicates perfectly inelastic demand. Any point on this curve would always have 0 elasticity.
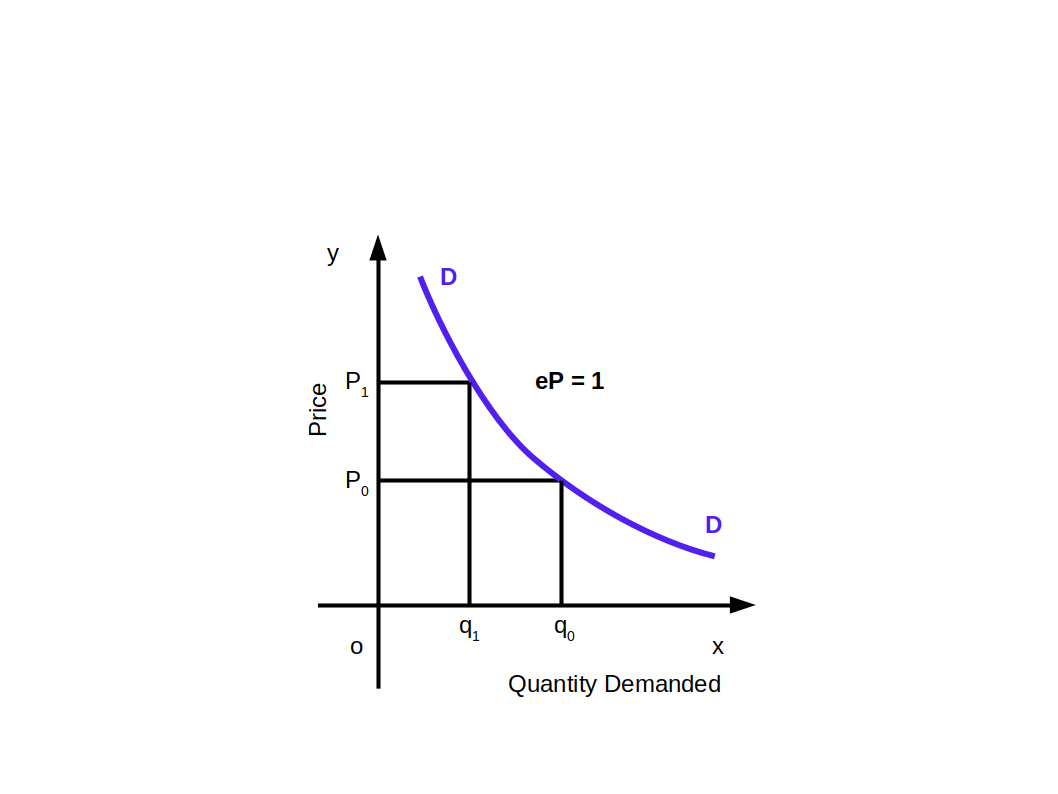
Similarly, all points on the rectangular hyperbola demand curve will have unitary elastic demand as shown in the above given Diagram.
Factors Determining Price Elasticity of Demand for a Good
Price elasticity of demand is influenced by several factors. They are briefly described below:
- Nature of the good: Elasticity of a good depends on whether it is a necessary or a luxury. If it is a necessary good elasticity would be low. If it is a luxury good it will have a high elastic demand.
- Availability of close substitutes: Substitute goods will always have highly elastic demand, while non- substitute goods will have inelastic demand.
- Proportion of income spent on the good: Consumers usually spend only a small portion of their income on certain goods like salt, match, etc. Elasticity of these goods will be low.
- Income of the consumer: As far as high income consumers are concerned elasticity of demand of most of the goods they use will be low. But the goods used by the poor would have high elasticity.
- Price of the good: Elasticity of demand for cheap goods will be low, and that of expensive and luxury goods would be high.
- Time period: Elasticity is high for long period compared to short period. This is because consumer can control consumption, during long period, by switching over to cheap substitutes.


