Chapter 16

Introduction

If we analyse two or more observations the central value may be the same but still there can be wide disparities in the formation of the distribution. For example, the AM of 2, 5 and 8 is 5; AM of 4, 5 and 6 is 5; AM of 1, 2 and 12 is 5; AM of 0, 1 and 14 is 5. Measures of dispersion will help us in understanding the important characteristics of a distribution.

This is explained with the help of another example.

Runs scored by three batsmen in a series of 5 one day matches are as given below:

Table 6.1 Cricket Scores
Days	Batsman 1	Batsman 2	Batsman 3
1	100	70	0
2	100	80	0
3	100	100	300
4	100	120	180
5	100	130	20
Total	500	500	500
Mean	100	100	100

Since the average is the same in all the three cases, one Is likely to conclude that these three batsmen are alike, But a close examination shall reveal that the distributions differ widely from one another. In case of the first batsman, each and every item is perfectly represented by the AM and there is no dispersion. In case of the second batsman, only one item is perfectly represented by the AM and the other items vary, but the variation is not too much. In case of the third batsman, not a single item is represented by the AM. All the items vary, and the variation is too large. Here we can see that the first batsman is consistent, while the third is inconsistent.

Now it is quite obvious that averages try to tell only the representative size of a distribution. To understand it better, we need to know the spread of various items also. So in order to express the data correctly, it becomes necessary to describe the deviation of the observations from the central value. This deviation of items-from the central value is called dispersion.

” The degree to which numerical data tend to spread about an average value is called the variation or dispersion of the data.” – Spiegel

The word dispersion means deviation or difference. In statistics, dispersion refers to deviation of various items of the series from its central value. Dispersion is the degree to which a numerical data tend to spread about an average value. Measure of dispersion is the method of measuring the dispersion or deviation of the different values from a designated value of the series. These measure, are also called averages of second order as they are averages of deviation taken from an average.

Objects of measuring variation

Measures of dispersion are useful in following respects:

1. To test the reliability of an average: Measures of dispersion enable us to know whether an average is really representative of the series. If the variability in the values of various items in a series is large the average is not so typical. On the other hand, if the variability is small, the average would be a representative value.
2. To serve as a basis for the control of the variability: A study of dispersion helps in identifying the causes of variability and in taking remedial measures.
3. To compare the variability of two or more series: We can compare the variability of two or more series by calculating relative measures of dispersion. The higher the degree of variability the lesser is the consistency or uniformity and vice versa.
4. To serve as a basis for further statistical analysis: Many powerful analytical tools in statistics such as correlation, regression, testing of hypothesis, analysis of fluctuations in time series, techniques of production control, cost control, etc., are based on measures of dispersion.

Methods of studying Dispersion

The following are the important methods:

1. Range
2. Quartile Deviation
3. Mean Deviation
4. Standard Deviation
5. Lorenz Curve

Range and quartile deviation measure the dispersion by calculating the spread within which the values lie. Mean deviation and standard deviation calculate the extent to which the values differ from the average. Lorenz curve is a graphical method of finding dispersion.

Absolute and Relative Measures of Dispersion

Absolute measures of dispersion are expressed in the same statistical unit in which the original data are given. In case two sets of data are expressed in different units, absolute measures of dispersion are not comparable. In such cases, relative measures are used.

A measure of relative dispersion is the ratio of measure of absolute dispersion to an appropriate average. It is also called coefficient of dispersion, as it is independent of the unit.

Range

Range is the simplest method of studying dispersion. It is the difference between the highest and the lowest values in a series.

$$ Range = L – S $$

where L= largest item; S = smallest item.

The relative measure corresponding to range, called the coefficient of range is obtained by applying the following formula:

$$ Coefficient \,of \,Range \,= \,{{\frac{L – S }{L + S}}} $$

Individual Series

Let us find Range and Coefficient of Range. The profits of a company for the last 8 years are given below.

Table 6.2
Year	Profit (in 000 Rs)
1985	40
1986	30
1987	80
1988	100
1989	115
1990	85
1991	210
1992	230

$$ Range = L – S $$

Here L = 230; S = 30.

Range = 230 – 30 = 200

$$ Coefficient \,of \,Range \,= \,{{\frac{L – S }{L + S}}} $$ $$ = \,{{\frac{230 – 30 }{230 + 30}}} $$ $$ = \,{{\frac{200 }{260}}} $$ $$ = \,{{0.77}} $$

Discrete Series

Let us find Range and Coefficient of Range for a discrete series.

Table 6.3
Size	Frequency
5	7
10	8
15	12
20	16
25	21
30	17
35	12
40	4

In order to find Range and Coefficient of Range, we should take the highest and the lowest values of size of items.

$$ Range = L – S $$

Here L = 40; S = 5.

Range = 40 – 5 = 35

$$ Coefficient \,of \,Range \,= \,{{\frac{L – S }{L + S}}} $$ $$ = \,{{\frac{40 – 5 }{40 + 5}}} $$ $$ = \,{{\frac{35}{45}}} $$ $$ = \,{{0.78}} $$

Continuous Series

For continuous series, range is calculated either by subtracting the lower limit of the lowest class from the upper limit of the highest class or by subtracting the mid-value of the lowest class from the midvalue of the highest class.

Let us find the range and coefficient of range of the following series:

Table 6.4
Daily Wage	Number of Workers
80 – 100	12
100 – 120	18
120 – 140	24
140 – 160	27
160 – 180	32
180 – 200	20

$$ Range = L – S $$

Here L = 200; S = 80.

Range = 200 – 80 = 120

$$ Coefficient \,of \,Range \,= \,{{\frac{L – S }{L + S}}} $$ $$ = \,{{\frac{200 – 80 }{200 + 80}}} $$ $$ = \,{{\frac{120}{280}}} $$ $$ = \,{{0.43}} $$

Let us find the range and coefficient of range of the following series where only midpoints are given:

Table 6.5
Class midpoints	Frequency
2	3
5	5
8	6
11	8
14	6
17	4
20	1

$$ Range = L – S $$

Here L = 20; S = 2.

Range = 20 – 2 = 18

$$ Coefficient \,of \,Range \,= \,{{\frac{L – S }{L + S}}} $$ $$ = \,{{\frac{20 – 2 }{20 + 2}}} $$ $$ = \,{{\frac{18}{22}}} $$ $$ = \,{{0.82}} $$

Quartile Deviation

We have seen that range is the simplest to understand and easiest to compute. But range as a measure of dispersion has certain limitations. The presence of even one extreme item (high or low) in a distribution can reduce the utility of range as a measure of dispersion. Since it is based on two extreme items (highest and lowest) it fails to take into account the scatter within the range. Hence we need a measure of dispersion to overcome these limitations of range. Such a measure of dispersion is called quartile deviation. In the previous chapter we studied quartiles. Quartiles are those values which divide the series into four equal parts. Hence we have three quartiles-Q₁, Q₂, and Q₃. Q₁ is the lower quartile wherein \( { \frac{{1}}{{4}}} \)^th of the total observations lie below it and \( { \frac{{3}}{{4}}} \)^th above it. Q₂ is same as median which divides the series into two equal parts. Q₃ is the upper quartile, \( { \frac{{3}}{{4}}} \)^th of the value falls below it and \( { \frac{{1}}{{4}}} \)^th above.

We have already studied the value of Q₁ and Q₃ for individual, discrete and continuous series, hence not repeated.

Upper and lower quartile ( Q₁ and Q₃ ) are used to calculate inter-quartile range.

$$ \mathbf {Inter-quartile\, range \,= Q_3\,-\,Q_1} $$ Half of inter-quartile range is called quartile deviation.

Quartile deviation (semi inter-quartile range) is defined as half the distance between the third and first quartiles.

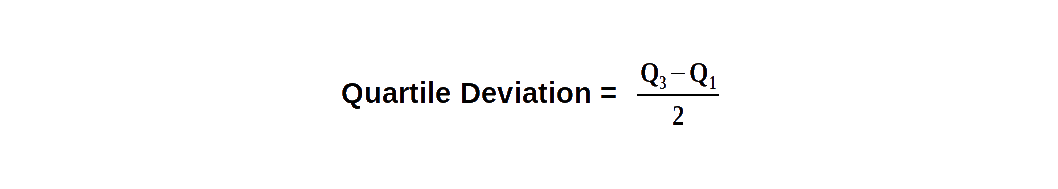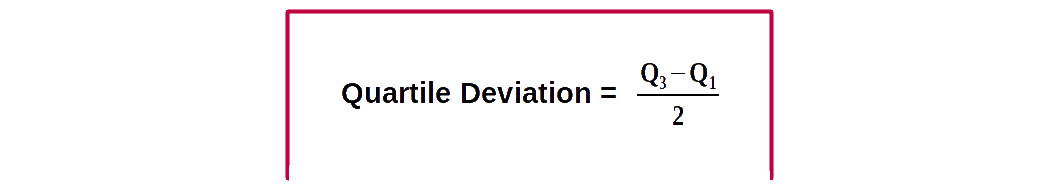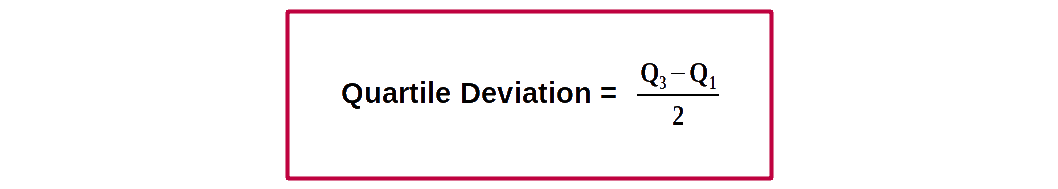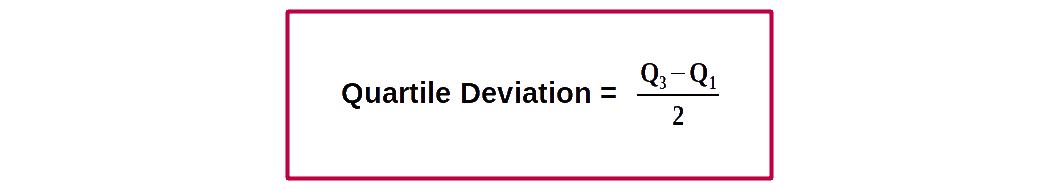
Quartile Deviation and inter quartile range are absolute measures of dispersion. The relative measure is coefficient of Quartile Deviation (Q.D)

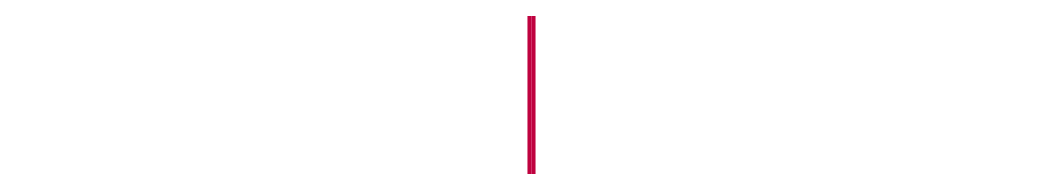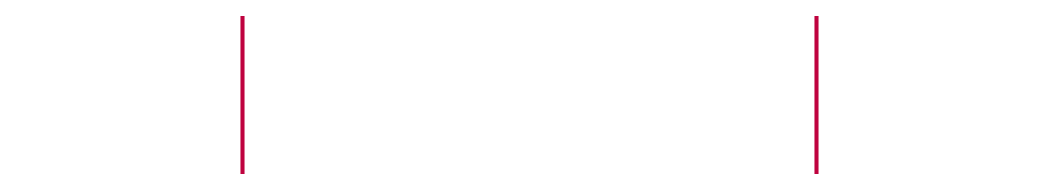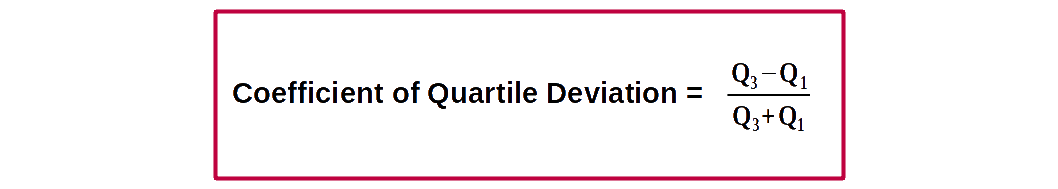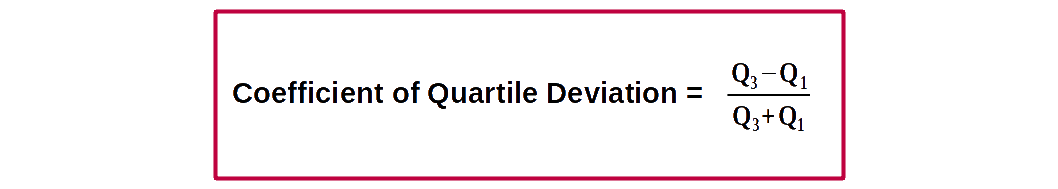
Individual Series

STEPS:-

Let us find the value of quartile deviation and its coefficient from the following data.

Table 6.6
Roll No.	Marks
1	20
2	28
3	40
4	12
5	30
6	15
7	50

We need to arrange Marks given in ascending order.

12, 15, 20, 28, 30, 40. 50

$$ Q_1 \,= \,Size \,of\,\Biggl[{{\frac{N + 1 }{4}}}\Biggl]^{th} item $$ $$ = \,Size \,of\,\Biggl[{{\frac{7 + 1 }{4}}}\Biggl]^{th} item $$ $$ = 2^{nd}\,item$$ Size of 2^nd item is 15. Thus Q₁ = 15

$$ Q_3 \,= \,Size \,of\,3\Biggl[{{\frac{N + 1 }{4}}}\Biggl]^{th} item $$ $$ Q_3 \,= \,Size \,of\,3\Biggl[{{\frac{7 + 1 }{4}}}\Biggl]^{th} item $$ $$ = Size\, of\, 6^{th}\,item$$ Size of 6^th item = 40; Q₃ = 40.

$$Q.D \,=\, {{{\frac{Q_3 – Q_1}{2}} }} $$ $$ = \,{{{\frac{40 – 15}{2}} }} $$ $$ = \,{{{\frac{25}{2}} }} $$ $$ = \, 12.5 $$ $$Coefficient \,of \,Q.D \,=\, {{{\frac{Q_3 – Q_1}{Q_3 + Q_1}} }} $$ $$=\, {{{\frac{40 – 15}{40 + 15}} }} $$ $$=\, {{{\frac{25}{55}} }} $$ $$ = \, 0.455 $$

Discrete Series

STEPS:-

Let us find the value of inter-quartile range, quartile deviation and its coefficient from the following data.

Table 6.7
Marks	No. of Students
10	4
20	7
30	15
40	8
50	7
60	2

Now we can create a table showing cumulative frequency (C.F) .

Table 6.8
Marks	No. of Students	C.F
10	4	4
20	7	11
30	15	26
40	8	34
50	7	41
60	2	43

$$ Q_1 \,= \,Size \,of\,\Biggl[{{\frac{N + 1 }{4}}}\Biggl]^{th} item $$ $$ = \,Size \,of\,\Biggl[{{\frac{43 + 1 }{4}}}\Biggl]^{th} item $$ $$ = 11^{th}\,item $$ Size of 11^th item = 20; Q₁ = 20.

$$ Q_3 \,= \,Size \,of\,3\Biggl[{{\frac{N + 1 }{4}}}\Biggl]^{th} item $$ $$ = \,Size \,of\,3\Biggl[{{\frac{43 + 1 }{4}}}\Biggl]^{th} item $$ $$ = \,Size \,of\Biggl[{{\frac{3 × 44 }{4}}}\Biggl]^{th} item $$ $$ = Size\, of\, 33^{rd}\,item$$ Size of 33^rd item = 40; Q₃ = 40.

$$ Inter-quartile \,range \,=\, Q_3\, – \,Q_1 $$ $$ =\, 40\, – \,20 $$ $$ =\,20 $$ $$ Q.D \,=\, {{{\frac{Q_3 – Q_1}{2}} }} $$ $$ = \,{{{\frac{40 – 20}{2}} }} $$ $$ = \,{{{\frac{20}{2}} }} $$ $$ = \, 10 $$ $$ Coefficient \,of \,Q.D \,=\, {{{\frac{Q_3 – Q_1}{Q_3 + Q_1}} }} $$ $$ =\, {{{\frac{40 – 20}{40 + 20}} }} $$ $$ =\, {{{\frac{20}{60}} }} $$ $$ = \, 0.333 $$

Continuous Series

STEPS:-

In the following table the figures relating to the wages of 60 workers in a company are given. Let us calculate the inter quartile range, quartile deviation and its coefficient.

Table 6.9
Wages (₹)	No. of Workers
20 – 25	2
25 – 30	10
30 – 35	25
35 – 40	16
40 – 45	7

Now we can create a table showing cumulative frequency (C.F) .

Table 6.10
Wages (₹)	No. of Workers	C.F
20 – 25	2	2
25 – 30	10	12
30 – 35	25	37
35 – 40	16	53
40 – 45	7	60
	N = 60

$$ Q_1\,=\,Size\,of\,{{{\frac{N}{4}} }}^{th} item $$ $$ =\,{{{\frac{60}{4}} }} $$ $$ =\,15^{th} item $$ Q₁ lies in the class 30 – 35

$$ Q_1 \,= \,{ L + \frac{\frac{N}{4} – {cf}}{f} × h} $$ L = 30;

\( {\frac{N}{4}} \) = 15;

CF = 12;

f = 25;

h = 5

$$ Q_1 \,= \,{ 30 + \frac{{15} – {12}}{25} × 5} $$ $$ =\, 30 \,+\,0.6 $$ $$ =\,30.6 $$ $$ Q_3\,=\,Size\,of\,{{{\frac{3N}{4}} }}^{th} item $$ $$ =\,{{{\frac{3 × 60}{4}} }} $$ $$ =\,{{{\frac{180}{4}} }} $$ $$ =\,45^{th} item $$ Q₃ lies in the class 35 – 40

$$ Q_3 \,= \,{ L + \frac{\frac{3N}{4} – {cf}}{f} × h} $$ L = 35;

\( {\frac{3N}{4}} \) = 45;

CF = 37;

f = 16;

h = 5

$$ Q_3 \,= \,{ 35 + \frac{{45} – {37}}{16} × 5} $$ $$ =\, 35 \,+\,2.5 $$ $$ =\, 37.5 $$ $$ Inter-quartile \,range \,=\, Q_3\, – \,Q_1 $$ $$ =\, 37.5\, – \,30.6 $$ $$ =\,6.9 $$ $$ Q.D \,=\, {{{\frac{Q_3 – Q_1}{2}} }} $$ $$ = \,{{{\frac{37.5 – 30.6}{2}} }} $$ $$ = \,{{{\frac{6.9}{2}} }} $$ $$ = \, 3.45 $$ $$ Coefficient \,of \,Q.D \,=\, {{{\frac{Q_3 – Q_1}{Q_3 + Q_1}} }} $$ $$ =\, {{{\frac{37.5 – 30.6}{37.5 + 30.6}} }} $$ $$ =\, {{{\frac{6.9}{68.1}} }} $$ $$ = \, 0.101 $$

MERITS OF QUARTILE DEVIATION

• It is easily computed and readily understood.
• It is not affected by extreme items.
• It can be computed even for an open end distribution.
• It is superior and more reliable than the range.

DEMERITS OF QUARTILE DEVIATION

• It is not based on all the items in a series.
• It is not based on all the observations.
• It is not capable of further algebraic treatment.
• It does not indicate variation of items from the average.
• Its value is very much affected by sampling fluctuations.

Mean Deviation

Even though Range and Quartile Deviation give an idea about the spread of individual items of a series, they do not try to calculate their dispersion from its average. If the variations of items were calculated from the average, such a measure of dispersion would through light on the formation of the series and the spread of items round the central value. Mean deviation (M.D) is such a measure of dispersion.

Mean deviation of a series is the arithmetic average of the deviations of various items from a measure of central tendency. In aggregating the deviations, algebraic signs of the deviations are not taken into account. It is because, if the algebraic signs were taken into account, the sum of deviations from the mean should be zero and that from median is nearly zero. Theoretically the deviations can be taken from any of the three averages, namely, arithmetic mean, median or mode; but, mode is usually not considered as it is less stable. Between mean and median, the latter is supposed to be better because, the sum of the deviations from the median is less than the sum of the deviations from the méan.

While doing problems, if the type of the average is mentioned, we take that average: otherwise we consider mean or median as the case may be.

This measure of dispersion has found favour with economists and business men due to its simplicity in calculation. For forecasting of business cycles, this measure has been found more useful than others. it is also good for small sample studies where elaborate statistical analysis is not needed.

Where D represents deviations from mean or median, ignoring signs, and N the total number of items.

MD is an absolute measure of dispersion. The relative measure of MD is coefficient of MD, defined as:

$$ \mathbf {Coefficient\,of\,MD\,=\,{{{\frac{MD}{Mean}} }}} $$

Mean Deviation: Points to remember.

1. It is based on all items
2. A change in even one value will affect it
3. Value will be least, if we are calculating it from median
4. Value will be higher, if calculated from the mean
5. Since it ignores signs of deviations, it is not suitable for open-end distribution

Mean Deviation from Arithmetic Mean

Individual Series

STEPS:-

• Find Mean using the equation \( {{{\frac{ΣX}{N}} }} \)

• Take deviations of individual values from mean, |d| (modulus) = (x – X̄), ignoring signs

• MD_X̄ = \( {{{\frac{Σ|D|}{N}} }} \) (N = number of items)

Relative measure of MD is coefficient of MD. Coefficient of MD = \( {{{\frac{MD}{Mean}} }} \)

Let us find the value of mean deviation and its coefficient from the following data.

Table 6.11
Roll No.	Marks
1	12
2	18
3	23
4	18
5	25
6	15
7	9
8	14
9	6
10	23
11	19
12	10

$$N\,=\,12$$ $$ X̄\,=\, {{{\frac{ΣX}{N}} }} $$ $$ =\, {{{\frac{192}{12}} }} $$ $$ =\,16 $$ Now we need to find modulus d. For that we creates a table as shown below.

Table 6.12
Roll No.	X (Marks)	|D| = |X – X̄| = |X – 16|
1	12	4
2	18	2
3	23	7
4	18	2
5	25	9
6	15	1
7	9	7
8	14	2
9	6	10
10	23	7
11	19	3
12	10	6
N = 12		Σ|D| = 60

$$ MD \,from \,X̄ \,=\,{{{\frac{Σ|D|}{N}} }} $$ $$ =\,{{{\frac{60}{12}} }} $$ $$ =\,5 $$ $$ Coefficient \,of\, MD \,=\,{{{\frac{MD}{Mean}} }} $$ $$ =\,{{{\frac{5}{16}} }} $$ $$ =\,0.3125 $$

Discrete Series

STEPS:-

Let us find the value of mean deviation and its coefficient from the following data.

Table 6.13
Value	Frequency
8	2
13	5
15	9
21	14
24	7
28	7
29	4
30	2

We need to find fx, |D| and f|D|. This is shown in the below given table.

Table 6.14
Value	f	fx	|D| = |X – X̄| = |X – 21|	f|D|
8	2	16	13	26
13	5	65	8	40
15	9	135	6	54
21	14	294	0	0
24	7	168	3	21
28	7	196	7	49
29	4	116	8	32
30	2	60	9	18
	N = 50	ΣfX = 1050		Σf|D| = 240

$$ X̄\,=\, {{{\frac{ΣfX}{N}} }} $$ $$ =\, {{{\frac{1050}{50}} }} $$ $$ =\,21 $$ $$ MD \,from \,X̄ \,=\,{{{\frac{Σf|D|}{N}} }} $$ $$ =\,{{{\frac{240}{50}} }} $$ $$ =\,4.8 $$ $$ Coefficient \,of\, MD \,=\,{{{\frac{MD}{Mean}} }} $$ $$ =\,{{{\frac{4.8}{21}} }} $$ $$ =\,0.23 $$

Continuous Series

In order to calculate MD and its coefficient for continuous series, we use the same method described earlier. Here we the devition from midvalues of classes. That is, we take midpoint as X here.

STEPS:-

Let us find MD from AM for the following series relates the marks of 20 students:

Table 6.15
Marks	No. of Students
0 – 10	2
10 – 20	2
20 – 30	5
30 – 40	5
40 – 50	3
50 – 60	2
60 – 70	1

We need to find midvalue (m), fm, |d| and f|D|. This is shown in the below given table.

Table 6.16
Class	f	X = m	fm	|D| = |m – X̄| = |m – 32.5|	f|D|
0-10	2	5	10	27.5	55
10-20	2	15	30	17.5	35
20-30	5	25	125	7.5	37.5
30-40	5	35	175	2.5	12.5
40-50	3	45	135	12.5	37.5
50-60	2	55	110	22.5	45
60-70	1	65	65	32.5	32.5
	Σf = 20		Σfm = 650		Σf|D| = 255

$$ X̄\,=\, {{{\frac{Σfm}{Σf}} }} $$ $$ =\, {{{\frac{650}{20}} }} $$ $$ =\,32.5 $$ $$ MD \,from \,X̄ \,=\,{{{\frac{Σf|D|}{Σf}} }} $$ $$ =\,{{{\frac{255}{20}} }} $$ $$ =\,12.75 $$

Mean Deviation from Median

Individual Series

STEPS:-

• Arrange the data in ascending order

• Compute the median

  Median = Size of \( {{{\frac{N + 1}{2}} }}^{th} \) item

• Take deviation of individual values from median. i.e., |d| = X – Median (ignoring signs)

MD_Median = \( {{{\frac{Σ|D|}{N}} }} \) ( N = Number of items)

Coefficient of MD = \( {{{\frac{MD}{Median}} }} \)

Let us find the value of mean deviation and its coefficient from the following data. We can calculate mean deviation from median.

4000, 4200, 4400, 4600, 4800

$$ Median\, =\, {{{\frac{N + 1}{2}} }}^{th} item $$ $$ =\, {{{\frac{5 + 1}{2}} }}^{th} item $$ $$ =\, {{{\frac{6}{2}} }}^{th} item $$ $$ =\, 3^{rd} item $$ $$ =\, 4400 $$

Table 6.17
Deviation from Median 4400
Income	|D|
4000	400
4200	200
4400	0
4600	200
4800	400
N = 5	Σ|D| = 1200

$$ MD_Median\, = \, {{{\frac{Σ|D|}{N}} }} $$ $$ = \, {{{\frac{1200}{5}} }} $$ $$ =\, 240 $$ $$ Coefficient \,of\, MD\, =\, {{{\frac{MD}{Median}} }} $$ $$ = \, {{{\frac{240}{4400}} }} $$ $$ =\, 0.054 $$

Discrete Series

STEPS:-

Let us find the value of mean deviation from the following data. We can calculate mean deviation from median.

Table 6.18
x	f
2	1
4	4
6	6
8	4
10	1

We need to find midvalue |d|, f|D| and cf. This is shown in the below given table.

$$ Median\, =\, {{{\frac{N + 1}{2}} }}^{th} item $$ $$ =\, {{{\frac{16 + 1}{2}} }}^{th} item $$ $$ =\, {{{\frac{17}{2}} }}^{th} item $$ $$ =\, 8.5^{th} item $$ $$ =\, 6 $$ $$ ∴\, Median\,=\, 6 $$

$$ MD_{Median}\, = \, {{{\frac{Σf|D|}{Σf}} }} $$ $$ = \, {{{\frac{24}{16}} }} $$ $$ =\, 1.5 $$

Continuous Series

STEPS:-

Let us find the value of mean deviation and coefficient of mean deviation from the following data. We can calculate mean deviation from median.

Table 6.20
Age	No. of Person
0 – 10	6
10 – 20	9
20 – 30	20
30 – 40	5
40 – 50	10

We need to find cf, midvalue (m), |d| and f|D|. This is shown in the below given table.

$$ Median \,class \,= \,Size \,of \, {{{\frac{N}{2}} }}^{th} item $$ $$ = \,{{{\frac{50}{2}} }}^{th} item $$ $$ = \,25^{th} item $$ 25^th item lies in the class 20 – 30

$$ Median \,= \,{ L + \frac{\frac{N}{2} – {cf}}{f} × h} $$ $$ = \,{ 20 + \frac{{25} – {15}}{20} × 10} $$ $$ = \,{ 20 \,+ \,5 \,=\, 25} $$ $$ MD_{Median} \,=\, {{{\frac{Σf|D|}{Σf}} }} $$ $$ =\, {{{\frac{460}{50}} }} $$ $$ =\, 9.2 $$ $$ Coefficient \,of \,MD \,= {{{\frac{MD_{Median}}{Median}} }} $$ $$ =\, {{{\frac{9.2}{25}} }} $$ $$ =\, 0.368 $$

Standard Deviation

The technique of the calculation of mean deviation is mathematically illogical as in its calculation the algebraic signs are ignored. This drawback is removed in the calculation of standard deviation. One of the easiest ways of doing away with algebraic signs is to square the figures and this process is adopted in the calculation of standard deviation. In the calculation of SD, first the AM is calculated and the deviations of. various items from the AM are squared. The squared deviations are summed up and the sum is divided by the number of items, The positive square root of the number will give SD. That is, SD is the positive square root of the mean of squared deviations from mean.

The concept of standard deviation was first used by Karl Pearson in the year 1893. It is the most commonly used measure of dispersion. It satisfies most of the properties laid down for an ideal measure of dispersion. Note that SD is calculated from AM only. Just as mean is the best measure of central tendency, standard deviation is the best measure of dispersion. Standard deviation is calculated on the basis of mean only.

” Standard deviation is defined as the square root of the arithmetic average of the squares of deviations taken from the arithmetic average of a series. “

It is also known as the root-mean-square deviation for the reason that it is the square root of the mean of the squared deviations from AM.

Standard deviation is denoted by the Greek letter σ (small letter ‘sigma’).

The term variance is used to describe the square of the standard deviation. The term was first used by R. A. Fisher in 1913.

Standard deviation is an absolute measure of dispersion. The corresponding relative measure is called coefficient of SD. Coefficient of variation is also a relative measure. A series with more coefficient of variation is regarded as less consistent or less stable than a series with less coefficient of variation.

Symbolically,

Individual Series

Different methods are used to calculate standard deviation of individual series. All these methods result in the same value of standard deviation. These are given below:

Actual Mean Method

Let us find standard deviation for the following data by actual mean method.

Height: 160, 160, 161, 162, 163, 163, 163, 164, 164, 170.

We need to find d and d², it is shown in the below given table.

$$ {\overline{X}}\,= \, {{{\frac{ΣX}{N}} }} $$ $$ = \, {{{\frac{1630}{10}} }} $$ $$ = \, 163 $$

Table 6.22
x	d = (X – x̅)=(X – 163)	d2
160	-3	9
160	-3	9
161	-2	4
162	-1	1
163	0	0
163	0	0
163	0	0
164	1	1
164	1	1
170	7	49
ΣX = 1630, N = 10		Σd2 = 74

$$ \mathbf{σ\, = \,\sqrt{\frac {Σd^{2}}{N}}} $$ $$ \mathbf{ = \,\sqrt{\frac {74}{10}}} $$ $$ \mathbf{ = \,\sqrt{7.4}} $$ $$ \mathbf{ = \,2.72} $$

Assumed Mean Method

Let us find standard deviation for the following data by assumed mean method.

Height: 160, 160, 161, 162, 163, 163, 163, 164, 164, 170.

We need to find d and d², it is shown in the below given table.

$$ Assumed \,Mean \,=\, 162 $$

Table 6.23
x	d = (X – 162)	d2
160	-2	4
160	-2	4
161	-1	1
162	0	0
163	1	1
163	1	1
163	1	1
164	2	2
164	2	2
170	8	64
	Σd = 10	Σd2 = 84

$$ \mathbf{σ\, = \,\sqrt{\frac{Σd^{2}}{N}\,-\,{\Bigl(\frac{Σd}{N}\Bigr)}^{2}} } $$ $$ \mathbf{σ\, = \,\sqrt{\frac{84}{10}\,-\,{\Bigl(\frac{10}{10}\Bigr)}^{2}} } $$ $$ \mathbf{ = \,\sqrt{8.4\,-\,1}} $$ $$ \mathbf{ = \,\sqrt{7.4}} $$ $$ \mathbf{ = \,2.72} $$

Direct Method

Let us find standard deviation for the following data by direct method.

Height: 160, 160, 161, 162, 163, 163, 163, 164, 164, 170.

We need to find x², it is shown in the below given table.

Table 6.24
x	x2
160	25600
160	25600
161	25921
162	26244
163	26569
163	26569
163	26569
164	26896
164	26896
170	28900
Σx = 1630	Σx2 = 265764

$$ \mathbf{σ\, = \,\sqrt{\frac{Σx^{2}}{N}\,-\,{\Bigl(\frac{Σx}{N}\Bigr)}^{2}} } $$ $$ \mathbf{σ\, = \,\sqrt{\frac{265764}{10}\,-\,{\Bigl(\frac{1630}{10}\Bigr)}^{2}} } $$ $$ \mathbf{ = \,\sqrt{26576.4\,-\,26569}} $$ $$ \mathbf{ = \,\sqrt{7.4}} $$ $$ \mathbf{ = \,2.72} $$

Step Deviation Method

Let us find standard deviation for the following data by step deviation method.

5, 10, 25, 30, 50.

We need to find d, d’, and d’². Deviations taken from 25 and common factor 5, it is shown in the below given table.

Table 6.25
x	d = (X – 25)	\( \mathbf{d’\, = \, {{{\frac{(x-25)}{5}} }}} \)	d’2
5	-20	-4	16
10	-15	-3	9
25	0	0	0
30	5	1	1
50	25	5	25
		Σd’ = -1	Σd’2 = 51

$$ \mathbf{σ\, = \,\sqrt{\frac{Σd’^{2}}{N}\,-\,{\Bigl(\frac{Σd’}{N}\Bigr)}^{2}} \,×\,c } $$ $$ \mathbf{ = \,\sqrt{\frac{51}{5}\,-\,{\Bigl(\frac{-1}{5}\Bigr)}^{2}} \,×\,5 } $$ $$ \mathbf{ = \,\sqrt{10.2\,-\,(.04)}\,×\,5} $$ $$ \mathbf{ = \,\sqrt{10.16}\,×\,5} $$ $$ \mathbf{ = \,3.187\,×5} $$ $$ \mathbf{ = \,15.936} $$

Discrete Series

Standard deviation can be calculated in four ways:

Actual Mean Method

Let us find standard deviation for the following data by actual mean method.

Table 6.26
x	f
6	3
7	6
8	9
9	13
10	8
11	5
12	4

We need to find fx, x, x² and fx², this is shown in the below given table.

$$ {\overline{X}}\,= \, {{{\frac{ΣfX}{Σf}} }} $$ $$ = \, {{{\frac{432}{48}} }} $$ $$ = \, 9 $$

$$ \mathbf{σ\, = \,\sqrt{\frac {Σfx^{2}}{Σf}}} $$ $$ \mathbf{ = \,\sqrt{\frac {124}{48}}} $$ $$ \mathbf{ = \,\sqrt{2.58}} $$ $$ \mathbf{ = \,1.6} $$

Assumed Mean Method

Let us find standard deviation for the following data by assumed mean method.

Table 6.28
x	f
6	3
7	6
8	9
9	13
10	8
11	5
12	4

We need to find d, d², x², fd and fd², this is shown in the below given table.

$$ \mathbf{σ\, = \,\sqrt{\frac{Σfd^{2}}{Σf}\,-\,{\Bigl(\frac{Σfd}{Σf}\Bigr)}^{2}} } $$ $$ \mathbf{ = \,\sqrt{\frac{172}{48}\,-\,{\Bigl(\frac{-48}{48}\Bigr)}^{2}} } $$ $$ \mathbf{ = \,\sqrt{3.58\,-\,1} } $$ $$ \mathbf{ = \,\sqrt{2.58} } $$ $$ \mathbf{ = \,1.6 } $$

Direct Method

Let us find standard deviation for the following data by direct method.

Table 6.30
x	f
6	3
7	6
8	9
9	13
10	8
11	5
12	4

We need to find fx, x² and fx², this is shown in the below given table.

$$ \mathbf{σ\, = \,\sqrt{\frac{Σfx^{2}}{Σf}\,-\,{\Bigl(\frac{Σfx}{Σf}\Bigr)}^{2}} } $$ $$ \mathbf{ = \,\sqrt{\frac{4012}{48}\,-\,{\Bigl(\frac{432}{48}\Bigr)}^{2}} } $$ $$ \mathbf{ = \,\sqrt{83.58\,-\,81} } $$ $$ \mathbf{ = \,\sqrt{2.58} } $$ $$ \mathbf{ = \,1.61 } $$

Step Deviation Method

Let us find standard deviation for the following data by step deviation method.

Table 6.32
x	f
10	2
15	8
20	10
25	15
30	3
35	2

We need to find d, d’, fd’, d’² and fd’², this is shown in the below given table.

$$ \mathbf{σ\, = \,\sqrt{\frac{Σfd’^{2}}{Σf}\,-\,{\Bigl(\frac{Σfd’}{Σf}\Bigr)}^{2}} \,×\,c } $$ $$ \mathbf{ = \,\sqrt{\frac{71}{40}\,-\,{\Bigl(\frac{-25}{40}\Bigr)}^{2}} \,×\,5 } $$ $$ \mathbf{ = \,\sqrt{1.775\,-\,.391} \,×\,5 } $$ $$ \mathbf{ = \,\sqrt{1.384} \,×\,5 } $$ $$ \mathbf{ = \,1.1764 \,×\,5 } $$ $$ \mathbf{ = \,5.88} $$

Continuous Series

In continuous series we have class intervals for the variable. So we have to find out the mid-point for the various classes. Then the problem becomes similar to those of discrete series.

Standard deviation can be calculated in four ways:

Actual Mean Method

Let us find standard deviation for the following data by actual mean method.

We need to find m, fm, x (m – X, fx, x² and fx², this is shown in the below given table.

$$ {\overline{X}}\,= \, {{{\frac{Σfm}{Σf}} }} $$ $$ = \, {{{\frac{3650}{50}} }} $$ $$ = \, 73 $$

$$ \mathbf{σ\, = \,\sqrt{\frac {Σfx^{2}}{Σf}}} $$ $$ \mathbf{ = \,\sqrt{\frac {7600}{50}}} $$ $$ \mathbf{ = \,\sqrt{152}} $$ $$ \mathbf{ = \, {12.33}} $$

Assumed Mean Method

Let us find standard deviation for the following data by assumed mean method.

We need to find m, d (x – 75), d², fd and fd², this is shown in the below given table.

$$ \mathbf{σ\, = \,\sqrt{\frac{Σfd^{2}}{Σf}\,-\,{\Bigl(\frac{Σfd}{Σf}\Bigr)}^{2}} } $$ $$ \mathbf{= \,\sqrt{\frac{7800}{50}\,-\,{\Bigl(\frac{-100}{50}\Bigr)}^{2}} } $$ $$ \mathbf{= \,\sqrt{156\,-\,(-4)} } $$ $$ \mathbf{= \,\sqrt{156\,-\,4} } $$ $$ \mathbf{= \,\sqrt{152 }} $$ $$ \mathbf{= \,12.33} $$

Direct Method

Let us find standard deviation for the following data by direct method.

We need to find m, fm, and fm², this is shown in the below given table.

$$ \mathbf{σ\, = \,\sqrt{\frac{Σfm^{2}}{Σf}\,-\,{\Bigl(\frac{Σfm}{Σf}\Bigr)}^{2}} } $$ $$ \mathbf{ = \,\sqrt{\frac{274050}{50}\,-\,{\Bigl(\frac{3650}{50}\Bigr)}^{2}} } $$ $$ \mathbf{ = \,\sqrt{5481\,-\,5329} } $$ $$ \mathbf{ = \,\sqrt{152} } $$ $$ \mathbf{ = \,12.33 } $$

Step Deviation Method

Let us find standard deviation for the following data by step deviation method.

We need to find m, d’, fd’, d’² and fd’², this is shown in the below given table.

$$ \mathbf{σ\, = \,\sqrt{\frac{Σfd’^{2}}{Σf}\,-\,{\Bigl(\frac{Σfd’}{Σf}\Bigr)}^{2}} \,×\,c } $$ $$ \mathbf{ = \,\sqrt{\frac{78}{50}\,-\,{\Bigl(\frac{-10}{50}\Bigr)}^{2}} \,×\,10 } $$ $$ \mathbf{ = \,\sqrt{1.56 \,-\, .04} \,×\,10 } $$ $$ \mathbf{ = \,\sqrt{1.52} \,×\,10 } $$ $$ \mathbf{ = \,1.233 \,×\,10 } $$ $$ \mathbf{ = \,12.33 } $$

Properties of SD

Absolute and Relative Measures of Dispersion

Absolute measures of dispersion are expressed in the same statistical unit in which the original data are given such as rupees, tonnes, centimeters, etc. In case two sets of data are expressed in different units, absolute measures of dispersion are not comparable. In such cases, measures of relative dispersion should be used.

A measure of relative dispersion is the ratio of measure of absolute dispersion to an appropriate average. It is sometimes called a coefficient of dispersion because coefficient means a pure number that is independent of the unit of measurement. Greater the value of coefficient of dispersion more is the variability in a distribution (less consistency).

Lorenz Curve

Dispersion can be studied graphically also. For that we use what is called Lorenz Curve, after the name of Dr. Max O. Lorenz who first studied the dispersion of distribution of wealth by graphic method. This method is most commonly used to show inequality of income or wealth in a country and sometimes to make comparisons between countries or between different time periods. The Curve uses the information expressed in a cumulative manner to indicate the degree of variability. It is especially useful in comparing the variability of two or more distributions.

It has a draw back that it does not give any numerical value of the measure of dispersion. It merely gives a picture of the extent to which a series is pulled away from an equal distribution.

STEPS

Let us draw a Lorenz Curve for the following data and show the inequality in income.

Table 6.43
Income	Number of persons
0 – 5000	5
5000 – 10000	10
10000 – 20000	18
20000 – 40000	10
40000 – 50000	7

We need to create a table showing midpoints, cumulative midpoints, cumulative midpoints in percentages, frequency, cumulative frequency and cumulative frequency in percentage, this is shown in the below given table.

Note that for drawing Lorenz curve we take the frequency components along the x-axis and the corresponding value components along the y-axis. From the above table, we get the co-ordinates to be plotted as:

(x, y) = (10, 2.5), (30, 10), (66, 25), (86, 55), (100, 100)

From the above figure it is clear that along the line OC, the distribution of income proportionately equal; so that 5% of the income is shared by 5% of the population, 15% of the income is shared by 15% of the population, and so on. Hence we call OC as the line of equal distribution. The farther the curve OAC from this line, the greater is the variability present in the distribution, If there are two or more curves, the one which is the farthest from the line OC has the highest dispersion.