അദ്ധ്യായം 14
ഡാറ്റയുടെ അവതരണം
 ദത്തങ്ങൾ മൂന്ന് രീതിയിൽ അവതരിപ്പിക്കാം.
ദത്തങ്ങൾ മൂന്ന് രീതിയിൽ അവതരിപ്പിക്കാം.
- വസ്തുതാപരമായ /വിവരണാത്മകമായ അവതരണം.[Textual Presentation ]
- പട്ടികകൾ മുഖേനയുള്ള അവതരണം. [ Tabular Presentations ]
- ഡയഗ്രങ്ങളും ഗ്രാഫുകളും ഉപയോഗിച്ചുള്ള അവതരണം. [ Diagrammatic and Graphical Presentation ]
1.വസ്തുതാപരമായ അവതരണം.
[ Textual Presentation ]
ഈ രീതിയിൽ വിവരങ്ങൾ വസ്തുനിഷ്ഠമായി അവതരിപ്പിക്കുന്നു. അവതരിപ്പിക്കാനുള്ള വിവരങ്ങൾ വളരെ അധികം ഇല്ലങ്കിൽ ഈ അവതരണ രീതിയാണ് അനുയോജ്യം.
“ബസ് ചാർജ് വർദ്ധനയിൽ പ്രതിഷേധിച്ച് കൊണ്ട് 2018 ജൂലായ് 7ന് നടത്തിയ സമര ദിനത്തിൽ തൃശൂർ ടൗണിൽ 15 ബസുകൾ ഓടിച്ചപ്പോൾ 240 ബസുകൾ ഓടിച്ചില്ല.”

2.പട്ടികകൾ മുഖേനയുള്ള ദത്തങ്ങളുടെ അവതരണം.
[ Tabular Presentation of Data ]
ഒരുപട്ടികയിലെകോളങ്ങളിലും[ Columns ]പംക്തികളിലുമായി [ Rows ] ദത്തങ്ങളുടെ ക്രമത്തിലുള്ള സംഘാടനമാണ് പട്ടിക മുഖേനയുള്ള അവതരണം.കോളങ്ങൾ [ Columns ] ലംബമായും പംക്തികൾ[ Rows ]തിരശ്ചീനമായുംക്രമീകരിക്കുന്നു. ഈ രീതിയിൽ ദത്തങ്ങളുടെ ക്രമീകരണത്തെ “പട്ടിക” [ Table ] എന്ന് പറയുന്നു.
| പട്ടിക 14.1 ഗ്രാമ നഗര ഘടന [ 1971-2001 ] | ||
|---|---|---|
| വർഷം | ഗ്രാമം | നഗരം |
| 1971 | 80 | 20 |
| 1981 | 78 | 22 |
| 1991 | 74 | 26 |
| 2001 | 72 | 28 |
ദത്തങ്ങളെ പട്ടികയായി അവതരിപ്പിക്കുന്നതിന് നാലു രീതികളുണ്ട്.
- ഗുണാത്മകമായ തരംതിരിവ്. [ Qualitative Presentation ]
- പരിമാണാത്മകം.[ Quantitative Presentation ]
- കാലക്രമമനുസരിച്ച് അതായത് സമയാടിസ്ഥാനത്തിൽ അവതരണം. [ Temporal Presentation ]
- ഭൂമി ശാസത്രപരമായി അതായത് സ്ഥലമാനദണ്ഡത്തിൽ അവതരണം.[ Spatial Presentation ]
1.ഗുണാത്മകമായ തരംതിരിവ്.
[ Qualitative Classification ]
ഒരു പ്രത്യേക സവിശേഷത, സ്വഭാവം എന്നിവയുടെ അടിസ്ഥാനത്തിൽ ദത്തങ്ങളെ തരം തിരിക്കുന്ന രീതിയാണിത് സ്ത്രീ പുരുഷ വ്യത്യാസം, നിറം, സാക്ഷരത, മതം തുടങ്ങിയവ ഗുണാത്മകമായ തരംതിരിവിന് ഉദാഹരണങ്ങളാണ്.
| പട്ടിക 14.2 ഗുണാത്മകമായ തരംതിരിവ് [Qualitative Classification] |
|||
|---|---|---|---|
| Sex | Location | Total | |
| Rural | Urban | ||
| Male | 57.07 | 80.80 | 60.32 |
| Female | 30.03 | 63.30 | 33.57 |
| Total | 44.42 | 72.71 | 47.53 |
2.പരിമാണാത്മകം.
[ Quantitative ]
ഉയരം, തൂക്കം, എന്നിങ്ങനെയുള്ള അളന്നു തിട്ടപ്പെടുത്താവുന്ന വിധത്തിലുള്ള സവിശേഷതകളുടെ അടിസ്ഥാനത്തിൽ ദത്തങ്ങളെ തരംതിരിക്കുന്ന രീതിയാണിത്.
| പട്ടിക 14.3 തെരഞ്ഞെടുപ്പ് പഠനത്തിൽ പ്രതികരിച്ച 360 പേരുടെ പ്രായത്തെ അടിസ്ഥാന്നമാക്കിയുള്ള തരംതിരിവ്. [Quantitative Classification] |
||
|---|---|---|
| വയസ്സ് | പ്രതികരിച്ചവരുടെ എണ്ണം | ശതമാനം |
| 20-30 | 13 | 3.70 |
| 30-40 | 54 | 15.00 |
| 40-50 | 109 | 30.30 |
| 50-60 | 144 | 40.00 |
| 60-70 | 28 | 7.70 |
| 70-80 | 12 | 3.30 |
| ആകെ | 360 | 100 |
3.കാലക്രമമനുസരിച്ച് അതായത് സമയാടിസ്ഥാനത്തിൽ അവതരണം.
[ Temporal ]
സമയത്തെ അടിസ്ഥാനമാക്കി തരം തിരിക്കുകയാണങ്കിൽ അതിനെ സമയാടിസ്ഥാനത്തിലുള്ള തരംതിരിവ് എന്ന് പറയാം. കാലം / സമയം എന്നത് മണിക്കൂറുകളോ ദിവസങ്ങളൊ ആഴ്ചകളൊ മാസങ്ങളൊ വർഷങ്ങളൊ ആകാം.
| പട്ടിക 14.4 ഒരു സ്ഥാപനത്തിന്റെ 2007 മുതൽ 2010 വരെയുള്ള വാർഷിക വിൽപന. [Temporal Classification] | ||
|---|---|---|
| വർഷം | വിൽപന (In lakh) | |
| 2007 | 81.7 | |
| 2008 | 86.9 | |
| 2009 | 101.4 | |
| 2010 | 94.7 | |
4.ഭൂമി ശാസത്രപരമായി അതായത് സ്ഥലമാനദണ്ഡത്തിൽ അവതരണം.
[ Spatial Presentation]
തരംതിരിവ് സ്ഥലത്തെ അടിസ്ഥാനമാക്കി നടത്തുകയാണങ്കിൽ അതിനെ സ്ഥലപരമായ തരംതിരിവ് എന്ന് പറയുന്നു. സ്ഥലം എന്നത് ഗ്രാമം, പട്ടണം, ജില്ല, സംസ്ഥാനം,ഉപഭൂഖണ്ഡം എന്നിങ്ങനെ ഉള്ളവയാകാം.
| പട്ടിക 14.5 ഇന്ത്യയിൽ നിന്നുള്ള കയറ്റുമതി വിഹിതം. [Spatial Classification] |
||
|---|---|---|
| രാജ്യം | കയറ്റുമതി വിഹിതം | |
| USA | 21.8 | |
| GERMANY | 5.6 | |
| UK | 5.7 | |
| RUSSIA | 2.1 | |
പട്ടികയുടെ ഭാഗങ്ങൾ.
(Parts of a Table)
ഒരു സാംഖ്യിക പട്ടികയ്ക്ക് അതൊരു റഫറൻസ് പട്ടികയോ സംഗ്രഹീത പട്ടികയോ ഏതുമാകടെ, താഴെ സൂചിപ്പിച്ച തരത്തിൽ പ്രധാനപ്പെട്ട പ്രവർത്തന ഘടകങ്ങൾ ഉണ്ടായിരിക്കണം.
- പട്ടിക നമ്പർ .(Table number)
- ശീർഷകം.(Title)
- തലക്കുറിപ്പ്: (Head note)
- പക്തിശീർഷകം.(Stub)
- ബോക്സ് ശീർഷകം.(Box title)
- അളവുകളുടെ യൂണിറ്റ്. ( Units of Measurement )
- ഉള്ളടക്കം അല്ലെങ്കിൽ പ്രവർത്തന മണഡലം.(Body or field)
- പ്രഭവ സൂചിക.(Source note)
- അടിക്കുറിപ്പുകൾ.( Footnotes)
1. പട്ടിക നമ്പർ. (Table number)
ഓരോ പട്ടികയ്ക്കും നമ്പർ നൽകണം. ഒരു പട്ടികയുടെ നമ്പർ 3.1 എന്ന് രേഖപ്പെടുത്തിയാൽ അത് ,മൂന്നാമത്തെ അദ്ധ്യായത്തിൽ ഒന്നാമത്തെ പട്ടികയാണന്ന് സൂചന തരുന്നു.
2. ശീർഷകം. (Title)
ഓരോ പട്ടികയ്ക്കും ഓരോ ശീർഷകം നൽകണം. പട്ടികയിലെ ഉള്ളടക്കം സംബന്ധിച്ച ഒരു വിശദീകരണം ശീർഷകം കൊടുക്കുന്നു. പട്ടികയുടെ മുകൾവശത്തായിട്ടാണ് ശീർഷകം ചേർക്കുക. എന്ത്, എവിടെ, എപ്പോൾ, എന്നിങ്ങനെയുള്ള ചോദ്യങ്ങൾക്ക് പൂർണ്ണമായ ഒരു ശീർഷകം ഉത്തരം നൽകേണ്ടതുണ്ട്.
3. തലക്കുറിപ്പ്. ( Head note )
ഹ്രസ്വമായ ഒരു വിശദീകരണക്കുറിപ്പാണിത് ശീർഷകത്തെ (Title) കുറിച്ച് ഒരനുബന്ധ വിവരം തലക്കുറിപ്പ് നൽകുന്നു.
4. പംക്തിശീർഷകം. ( Stub / Row Heading )
പംക്തികളുടെ അഥവാ പംക്തി സമൂഹങ്ങളുടെ രൂപരേഖകളാണ് പംക്തി ശീർഷകം. ഇടത്തേ അറ്റത്തായാണ് ഇത് ചേർക്കുക.
5. ബോക്സ് ശീർഷകം. (Box title / Caption / Column Heading )
ഇത് കോളങ്ങളുടെ ശീർഷകത്തെ സൂചിപ്പിക്കുന്നു. കോളം എന്തിനെ പ്രതിനിധീകരിക്കുന്നുവെന്നത് തലവാചകം വിശദമാക്കുന്നു. ഒന്നോ അതിലധികമോ കോളം ശീർഷകങ്ങൾ തലവാചകത്തിൽ ഉൾകൊള്ളുന്നു. കോളം ശീർഷകത്തിനോരോന്നിനും കീഴെ ഉപശീർഷകങ്ങൾ ഉണ്ടായേക്കാം.
6. അളവുകളുടെ യൂണിറ്റ്. ( Units of Measurement )
പട്ടികയിലെ അക്കങ്ങളുടെ അളവിന്റെ യൂണിറ്റ് ശീർഷകത്തോടൊപ്പം വ്യക്തമാക്കിയിരിക്കണം. അക്കങ്ങൾ വലുതാണെങ്കിൽ അത് റൗണ്ട് ഓഫ് ചെയ്യുകയും ഏത് രീതിയിലാണ് ചെയ്തതെന്ന് സൂചിപ്പിക്കുകയും വേണം.
7. ഉള്ളടക്കം അല്ലെങ്കിൽ പ്രവർത്തന മണ്ഡലം. (Body or field)
പട്ടികയുടെ ഉള്ളടക്കത്തിൽ സംഖ്യാ സംബന്ധമായ വിവരങ്ങൾ അടങ്ങുന്നു. ഒരു പട്ടികയുടെ ഏറ്റവും പ്രധാനപ്പെട്ട ഭാഗമാണിത്. ഉള്ളടക്കം സാധാരണയായി ഇടത്ത് നിന്നും വലത്തോട്ട് പംക്തികളിലൂടെയും(raw) മുകളിൽ നിന്ന് താഴേക്ക് കോളങ്ങളിലൂടെയുമാണ് (columns)വിന്യസിക്കുന്നത്.
8. പ്രഭവ സൂചിക.(Source note)
പട്ടികയിലെ വിവരം എവിടന്നാണോ സ്വീകരിച്ചിട്ടുള്ളത് ആ പ്രഭവത്തെ ഇത് സൂചിപ്പിക്കുന്നു. ലദ്യമായ വിവരങ്ങൾ പരിശോധിക്കാനും കൂടുതൽ വിവരങ്ങൾ ശേഖരിക്കാനും ഇതു പഠിതാവിനെ സഹായിക്കുന്നതോടൊപ്പം വിവരങ്ങളുടെ ആധികാരികത സൂചിപ്പിക്കുന്നതിനും പ്രഭവസൂചിക സഹായിക്കുന്നു. ഇത് എപ്പോഴും പട്ടികയുടെ താഴേയാണ് രേഖപ്പെടുത്തുക.
9.അടിക്കുറിപ്പുകൾ.( Footnotes)
പട്ടികയിലെ ചില പ്രത്യേക സൂചകങ്ങളുമായി, അല്ലങ്കിൽ, പുതിയ രേഖകളുമായി (Entry) ബന്ധപ്പെടുത്തി വിശദീകരണം നൽകുന്നതിനുദ്ദേശിച്ചുള്ള ഒരു സൂത്രവാക്യമോ (Phrase) പ്രസ്താവമോ ആണ് അടിക്കുറിപ്പ്.ഉള്ളടക്കത്തിന് തൊട്ട് താഴെയാണിത് കൊടുക്കുക. * , H, I ,തുടങ്ങിയ പ്രതീകങ്ങളിലൂടെ ഇത് സൂചിപ്പിക്കുന്നു.
ഡയഗ്രങ്ങൾ മുഖേനയുള്ള ദത്തെങ്ങളുടെ അവതരണം.
( Diagrammatic Presentation of Data )
ആകർഷകവും ബോദ്ധ്യപ്പെടുത്തുന്നതുമായ രീതിയിൽ സ്ഥിതിവിവര ഡാറ്റ അവതരിപ്പിക്കുന്ന ഏറ്റവും കാര്യക്ഷമമായ ഒരു രീതിയാണ് ഡയഗ്രം മുഖേനയുള്ള അവതരണം. പലതരത്തിലുള്ള ഡയഗ്രം രീതികൾ നിലവിലുണ്ട്.
പ്രധാനപ്പെട്ട ചില ഡയഗ്രം രീതികൾ.
- I ജ്യാമിതീയ ഡയഗ്രം.(Geometric Diagram)
- II ആവൃത്തി ഡയഗ്രം.(Frequency Diagram)
- III ഗണിതരേഖാ ഗ്രാഫ്.(Arithmetic Line Graph)
I.ജ്യാമിതീയ ഡയഗ്രം.
(Geometric Diagram)
പ്രധാനപ്പെട്ട ജ്യാമതീയ ഡയഗ്രങ്ങൾ.
- ബാർ ഡയഗ്രം. (Bar Diagrams)
- പൈ ഡയഗ്രം. (Pie Diagrams)
ബാർ ഡയഗ്രം നാല് തരത്തിലുണ്ട്.
- സിമ്പിൾ ബാർ ഡയഗ്രം. (Simple Bar Diagrams)
- മൾട്ടിപ്പിൾ ബാർ ഡയഗ്രം. (Multiple Bar Diagrams)
- കോംപണന്റ് ബാർ ഡയഗ്രം. (Component Bar Diagrams)
- ശതമാന ബാർ ആരേഖങ്ങൾ.(Percentage Bar Diagrams)
1. സിമ്പിൾ ബാർ ഡയഗ്രം. (Simple Bar Diagrams)
ഡാറ്റയുടെ ഓരോ ക്ലാസിനും നല്ല സ്പേസും തുല്യ വീതിയുമുള്ള സമചതുരത്തിലുള്ള ഒരു കൂട്ടം ബാറുകളും അടങ്ങിയതാണ് ബാർ ഡയഗ്രം.ഉയരമോ വീതിയൊ ആണ് ബാറിന്റെ വലിപ്പം നിശ്ചയിക്കുന്നത്.ബാറിന്റെ താഴ്ന്ന ഭാഗം ബേസ് ലൈനിൽ തൊടുന്ന വിധത്തിൽ ബാറിന്റെ ഉയരം പൂജ്യം യൂണിറ്റിൽ നിന്ന് തുടങ്ങുന്നു. ബാറുകളുടെ ഉയരം നോക്കി ദത്തങ്ങളെ മനസ്സിലാക്കാൻ കഴിയുന്നു.
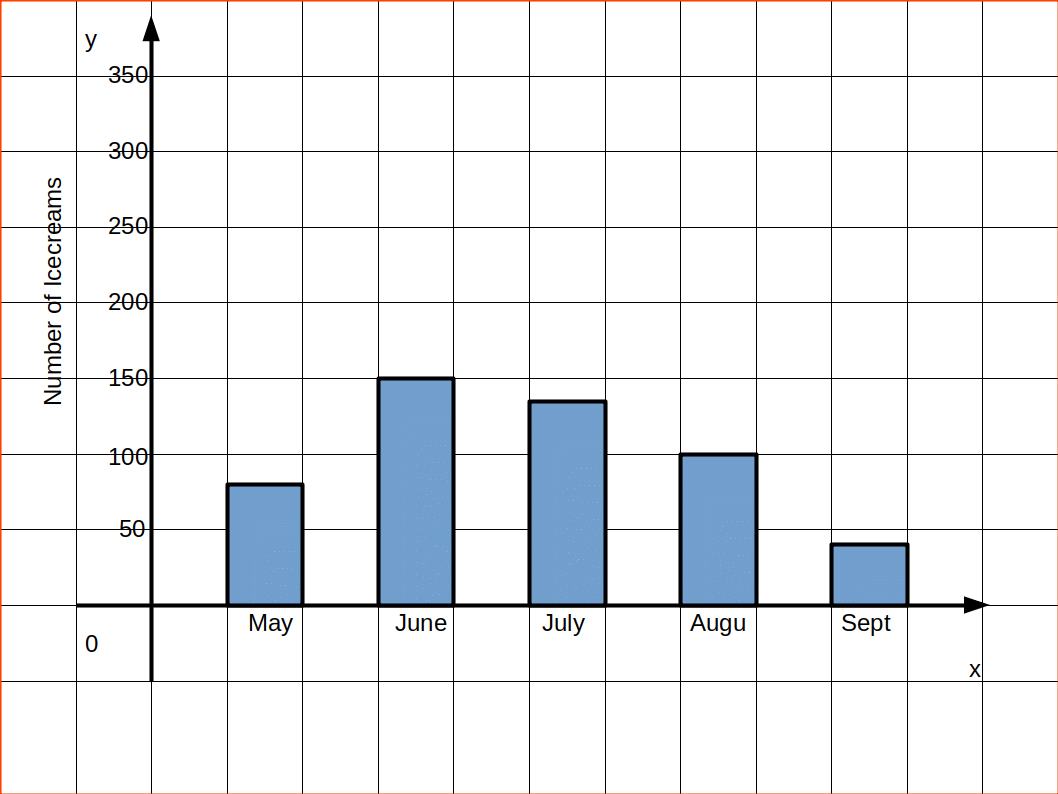
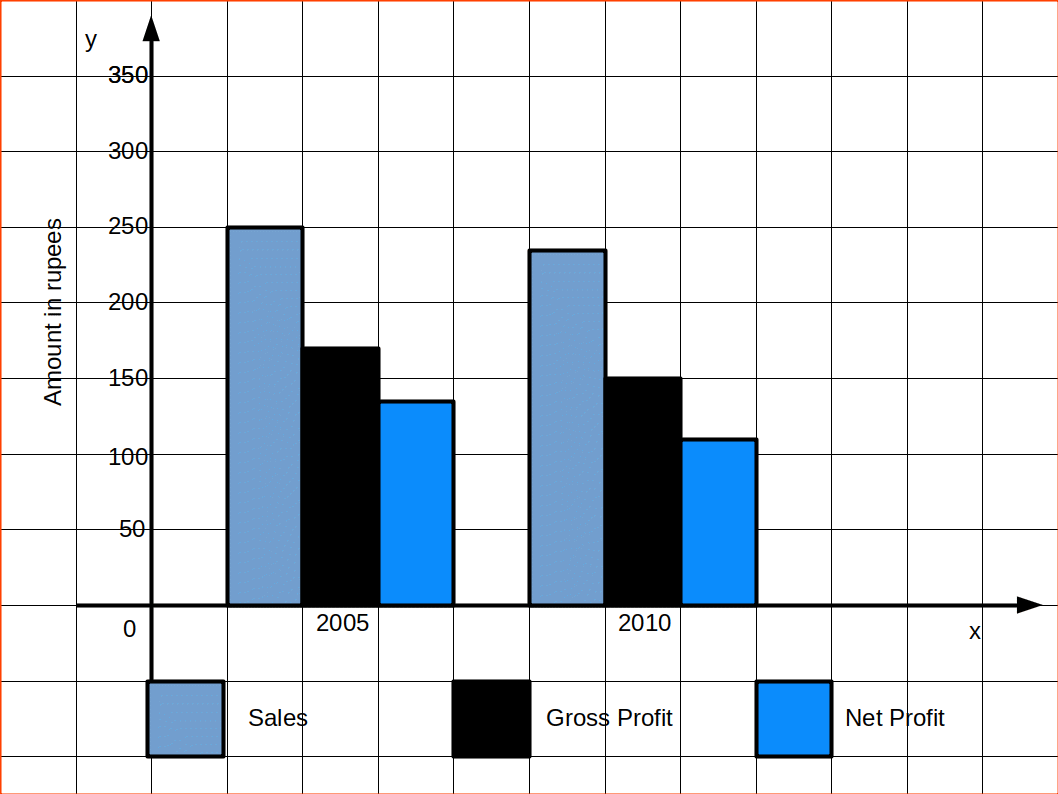
2. മൾട്ടിപ്പിൾ ബാർ ഡയഗ്രം. (Multiple Bar Diagrams)
രണ്ടൊ അതിലധികമോ ചരങ്ങളെ താരതമ്യപ്പെടുത്തുന്നതിനാണ് മൾട്ടിപ്പിൾ ബാർ ഡയഗ്രങ്ങൾ ഉപയോഗിക്കുന്നത്.
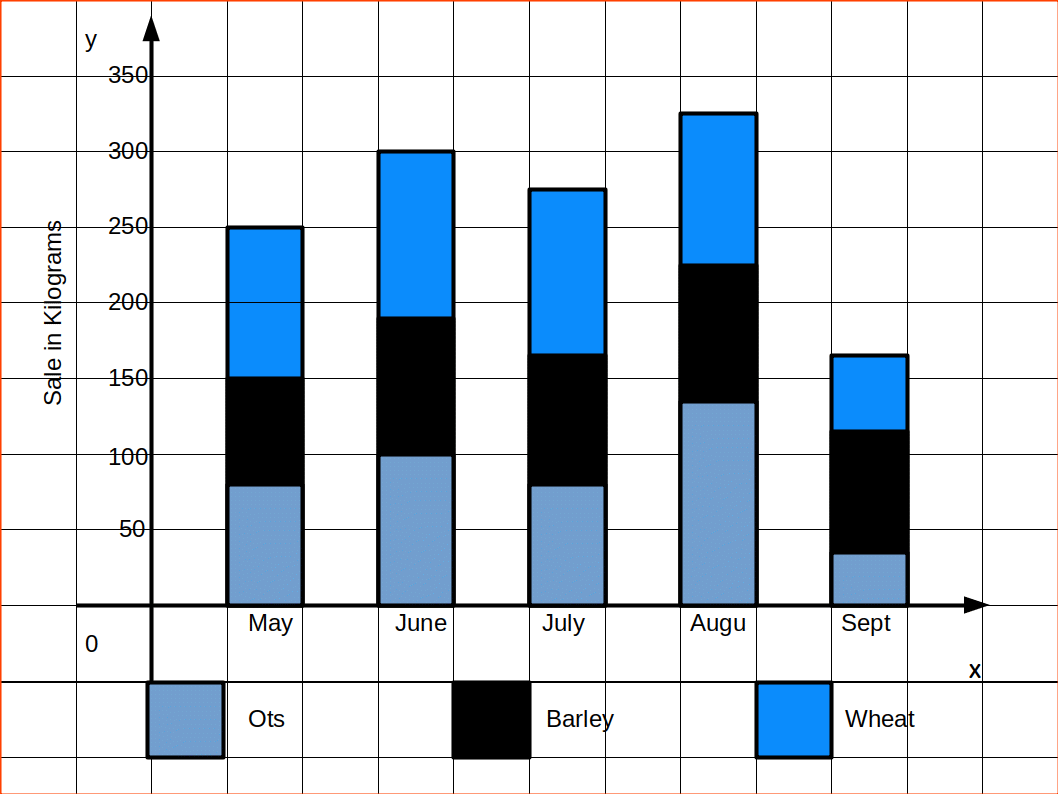
3. കോംപണന്റ് ബാർ ഡയഗ്രം. (Component Bar Diagrams)
ഒരു കോമ്പോണന്റ് ബാർ ഡയഗ്രത്തിൽ , നിർദ്ധിഷ്ഠപ്രതിഭാസത്തിന്റെ വലുപ്പത്തെ പ്രതിനിധീകരിക്കുന്ന ഓരോ ബാറും, അതിനെ വിവിധ ഘടകങ്ങളായി വീണ്ടും ഉപവിഭജനം പെയ്യുന്നു. മൊത്തത്തിൽ അതിന്റെ പങ്കിന് ആനുപാതികമായി ഓരോ ഘടകവും ബാറിന്റെ ഭാഗം കയ്യടക്കുന്നു.
ഘട്ടങ്ങൾ. (Steps involved in Creating Component Bar Diagram)
- ഓരോ ഡയഗ്രത്തിലുമുള്ള വിവിധ ഘടകങ്ങളെ ഒരേ ക്രമത്തിൽ നിലനിർത്തണം.
- രേഖയിൽ ഡയഗ്രം നിർമ്മിക്കുന്നത് ഡയഗ്രത്തിന്റെ ഉയരം ഡയഗ്രത്തിന്റെ മൊത്തം മൂല്യത്തോട് തുല്യമായ വിധത്തിലായിരിക്കണം.
- സാധാരണയായി അവലംബിക്കുന്ന രീതി ഡയഗ്രത്തിന്റെ അടിത്തറയിൽ നിന്ന് വ്യാപ്തിയുടെ ക്രമത്തിൽ ഏറ്റവും വലിയ ഘടകത്തിൽ നിന്ന് തുടങ്ങി ഏറ്റവും ചെറിയ ഘടകത്തിൽ അവസാനിക്കുന്ന വിധത്തിൽ ഡയഗ്രം നിർമ്മിക്കുക.
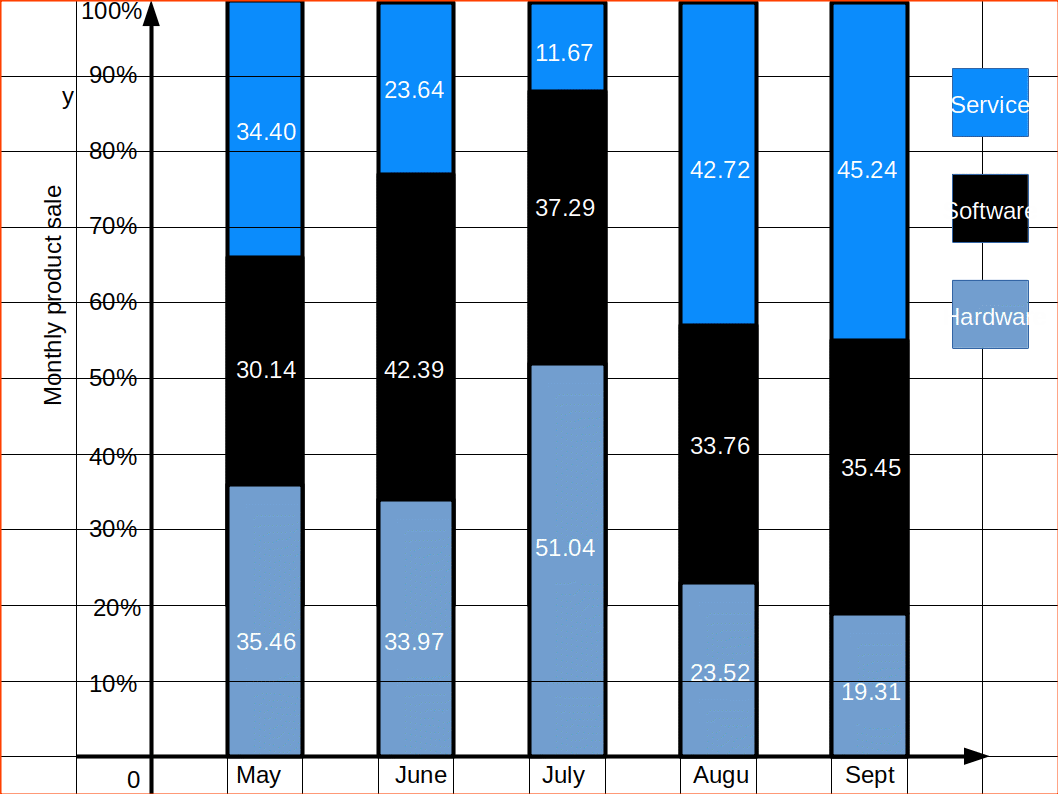
4. ശതമാന ബാർ ആരേഖങ്ങൾ.(Percentage Bar Diagrams)
ശതമാനത്തിന്റെ അടിസ്ഥാനത്തിൽ വരയ്ക്കപ്പെടുന്ന ഉപവിഭജിത ബാർ ആരേഖങ്ങൾ ശതമാന ബാർ ആരേഖങ്ങൾ എന്നറിയപ്പെടുന്നു. ശതമാന ബാർ ആരേഖങ്ങൾ തയ്യാറാക്കുമ്പോൾ ബാറുകൾ 100 ന് തുല്യമായി നിലനിർത്തുന്നു.ഈ ബാറുകളിൽ വിവിധ ഇനങ്ങളേ ഖണ്ഡങ്ങളായി അവതരിപ്പിക്കുന്നു.
നിർമ്മിക്കുന്ന ഘട്ടങ്ങൾ. (Steps involved in Creating Percentage Bar Diagram):-
- നൽകിയിരിക്കുന്ന അളവുകളെ ശതമാനത്തിലാക്കുക.
- ബെയ്സ് ലൈനിൽ നിന്നും ഡാറ്റയ്ക്ക് അനുയോജ്യമായ എണ്ണം ബാറുകൾ വരക്കുക.
- ശതമാനത്തിന്റെ അടിസ്ഥാനത്തിൽ ഓരോ ബാറിനെയും ഉപവിഭാഗങ്ങളാക്കുക.
- തിരിച്ചറിയുന്നതിനായി ഓരോ ഉപവിഭാഗങ്ങൾക്കും പ്രത്യേകം ഷൊയ്ഡ് നൽകുക.
| പട്ടിക 14.6 | ||
|---|---|---|
| ചെലവ് ഇനം | X | Y |
| രൂപയിൽ | രൂപയിൽ | |
| ഭക്ഷണം | 160 | 100 |
| വസ്ത്രം | 80 | 30 |
| വാടക | 60 | 40 |
| ലൈറ്റ്, ഇന്ധനം | 20 | 10 |
| പലവക | 80 | 20 |
| ആകെ | 400 | 200 |
| പട്ടിക 14.7 | ||||||
|---|---|---|---|---|---|---|
| ചെലവ് ഇനം | X | Y | ||||
| രൂപയിൽ | % | സഞ്ചിത % | രൂപയിൽ | % | സഞ്ചിത % | |
| ഭക്ഷണം | 160 | 40 | 40 | 100 | 50 | 50 |
| വസ്ത്രം | 80 | 20 | 60 | 30 | 15 | 65 |
| വാടക | 60 | 15 | 75 | 40 | 20 | 85 |
| ലൈറ്റ്, ഇന്ധനം | 20 | 5 | 80 | 10 | 5 | 90 |
| പലവക | 80 | 20 | 100 | 20 | 10 | 100 |
| ആകെ | 400 | 100 | 200 | 100 | ||
B. വൃത്താരേഖങ്ങൾ / പൈ ഡയഗ്രം. (Pie-Diagram) പൈ-ഡയഗ്രവും ഒരു കോംപോണന്റ് ഡയഗ്രമാണങ്കിലും കോംപണൻറ് ബാർ ഡയഗ്രം പോലെയല്ല. മൊത്തവും അവയുടെ വിഭാഗവും ഒന്നിച്ച് കാണിക്കേണ്ടി വരുമ്പോഴാണ് വൃത്താരേഖങ്ങൾ / പൈ-ഡയഗ്രം ഉപയോഗിക്കുന്നത്. ഒരു വൃത്തം മുഖേനയാണ് മൊത്തത്തെ കാണിക്കുക വൃത്തത്തിന്റെ വിവിധ ഭാഗങ്ങൾ വഴി വിഭാഗത്തെയും കാണിക്കുന്നു.
ഘട്ടങ്ങൾ. (Steps in Creating Pie-Diagrams)
- ആദ്യമായി വിവിധ ഘടകങ്ങളെ ശതമാനങ്ങളായി ആവിശ്കരിക്കുന്നു. പിന്നീട് ശതമാനങ്ങളെ 3.6 കൊണ്ട് ഗുണിക്കുന്നു. ഇങ്ങനെ ഓരോ ഘടകത്തിനുമുള്ള കോൺ (Angle 360/100) കിട്ടുന്നു.
- ഖണ്ഡങ്ങൾ വലുപ്പമനുസരിച്ച് വിന്യസിക്കപ്പെടുന്നു. ഏറ്റവും വലിയ ഭാഗം മുകളിലും മറ്റുള്ളവ ക്രമത്തൽ വലം വെച്ചു കൊണ്ടും കാണിക്കുന്നു.
| Table 14.8 School Transportation | ||
|---|---|---|
| Mode of transport | No. of students | |
| School bus | 18 | |
| Private vehicle | 6 | |
| Public transport | 12 | |
| By walking | 9 | |
| Table 14.9 School Transportation | |||
|---|---|---|---|
| Mode of transport | No. of students | Percentage | Angle |
| School bus | 18 | \( \mathbf{{{\frac{18 × 100}{45}} }} = 40 \) | 40×3.6 = 144º |
| Private vehicle | 6 | \( \mathbf{{{\frac{6 × 100}{45}} }} = 13.33 \) | 13.33×3.6 = 48º |
| Public transport | 12 | \( \mathbf{{{\frac{12 × 100}{45}} }} = 26.67 \) | 26.67×3.6 = 96º |
| By walking | 9 | \( \mathbf{{{\frac{9 × 100}{45}} }} = 20 \) | 20×3.6 = 72º |
| Total | 45 | 100 | 360º |

II. ആവൃത്തി ഡയഗ്രം.
(Frequency Diagram)
ആവൃത്തി വിതരണങ്ങൾ ഉൾക്കൊള്ളുന്ന ഡേറ്റയെ അവതരിപ്പിക്കുന്ന മാർഗ്ഗമാണ് ആവൃത്തി ഡയഗ്രങ്ങൾ.
- ഹിസ്റ്റോഗ്രാം.
- ആവൃത്തി ബഹുഭുജം.
- ആവൃത്തി വക്രം.
- ഒജീവ്.
1) ആയതാരേഖം (Histogram) സന്തത ആവൃത്തി വിതരണത്തിന്റെ ദ്വിമാന ആരേഖമാണിത്. വര്ഗ്ഗാന്തരാളങ്ങള് അടിസ്ഥാനമാക്കിയും (വീതിയായും) അതാത് ആവൃത്തികള് ഉയരമായി എടുത്തും ഉള്ളതായ ചതുരങ്ങളുടെ ഒരു സെറ്റ് ആണിത്. രണ്ടു ചതുരങ്ങള്ക്കുമിടയില് അകലം (gap) ഇടുകയില്ല. ആയതാരേഖം ബാര് ഡയഗ്രം പോലെതന്നെയാണ്. തൊട്ടുതൊട്ടു നില്ക്കുന്ന (adjacent) ലംബമാനമായ ആരേഖങ്ങളുടെ ഒരു പരമ്പരയായിട്ടാണ് ഇത് വരയ്ക്കുന്നത്. ആരേഖങ്ങള് X അക്ഷത്തില് തിരശ്ചിനമായിട്ടാണ് നിര്മ്മിക്കുന്നത്. ആരേഖങ്ങളുടെ വ്യാപ്തി (area) ആവൃത്തികള് പ്രതിനിധീകരിക്കപ്പെടുന്നതിന് ആനുപാതികമായിട്ടായിരിക്കും.
ചരങ്ങളെടുക്കുന്നത് എല്ലായ്പ്പോഴും X അക്ഷത്തിലും ആവൃത്തികള് എടുക്കുന്നത് Y അക്ഷത്തിലൂമാണ്, അതിന്റെ വര്ഗ്ലാന്തരാളങ്ങള്ക്ക് ആനുപാതികമായി സ്കെയിലിലെ ഒരകലം മുഖേന ഓരോ വര്ഗ്ഗവും പ്രതിനിധീകരിക്കപ്പെടുന്നു. വര്ഗ്ഗാന്തരാളങ്ങള് ഉടനീളം ഐക്യരൂപ്യമുള്ളതാണെങ്കില്, X അക്ഷത്തിന്മേലുള്ള ഓരോ സമകോണത്തിന്റെയും (Rectangle) അകലം ഒരേ രീതിയില് നിലനില്ക്കും. വര്ഗ്ഗാന്തരാളങ്ങള് ഐക്യരൂപ്യമുള്ളതല്ലെങ്കില് സമകോണത്തിന്റെ വീതിയും വ്യത്യസ്തമാകും. അക്ഷം ഓരോ വര്ഗ്ഗത്തിന്റെയും ആവൃത്തികളെ പ്രതിനിധാനം ചെയ്യുന്നു; സമകോണത്തിന്റെ ഉയരത്തെ പ്രതിനിധീകരിക്കുന്നു. ഇപ്രകാരം നമുക്കു സമകോണങ്ങളുടെ ഒരു ശ്രേണി ലഭിക്കുന്നു. ഓരോന്നിലും വര്ഗ്ലാന്തരാള അകലം അതിന്റെ വീതിയും, ആവ്യൃത്തിയകലം അതിന്റെ ഉയരവും ആയിത്തീരുന്നു. ആവൃത്തി സന്തതമാണെങ്കില് മാത്രമേ ആയതാരേഖങ്ങള് വരയ്ക്കാനാകൂ. അതു സന്തതമല്ലെങ്കില് അതിനെ സന്തതമാക്കിത്തീര്ക്കണം – വര്ഗ്ഗസീമകളെ (Class limits) ക്ലാസ് ബൗണ്ടറികളാക്കി മാറ്റിയും പിന്നീടതിന്റെ അടിസ്ഥാനത്തില് സമകോണങ്ങള് (Rectangles) ഉയര്ത്തിയും.| Table 14.10 | ||
|---|---|---|
| മാർക്കുകൾ | വിദ്യാർത്ഥികളുടെ എണ്ണം | |
| 0 – 10 | 5 | |
| 10 – 20 | 11 | |
| 20 – 30 | 19 | |
| 30 – 40 | 21 | |
| 40 – 50 | 16 | |
| 50 – 60 | 10 | |
| 60 – 70 | 8 | |
| 70 – 80 | 6 | |
| 80 – 90 | 3 | |
| 90 – 100 | 1 | |
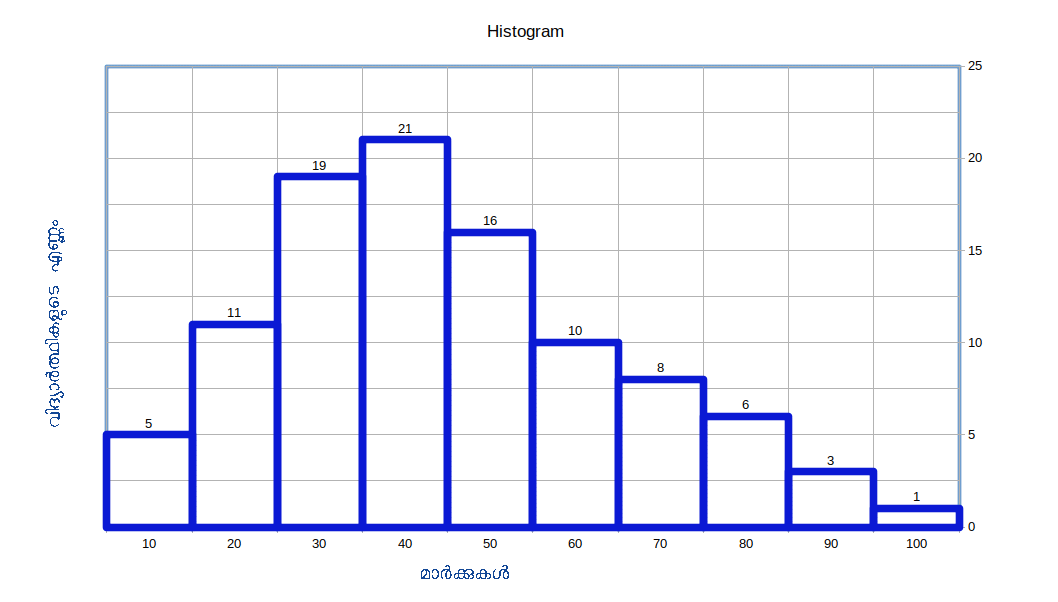
വർഗ്ഗാന്തരാളങ്ങൾ തുല്യമല്ലാതെ വരുമ്പോള് (When class intervals are unequal)
വര്ഗ്ലാന്തരാളങ്ങള് തുല്യമല്ലാതാകുമ്പോള് അവയ്ക്കു തിരുത്ത് നല്കണം. ഇതു ശരിപ്പെടുത്തുന്നതിന് നാം ഏറ്റവും താഴ്ന്ന വര്ഗ്ഗാന്തരാളമുള്ള വര്ഗ്ഗത്തെയെടുക്കുകയും ഇതര വര്ഗ്ഗങ്ങളിലെ ആവൃത്തികള് ശരിപ്പെടുത്തുകയും ചെയ്യുന്നു.
 എന്നതു മുഖേന, അനുയോജ്യമായ പൊരുത്തപ്പെടൂത്തല് ഘടകത്തെക്കൊണ്ട് നിര്ദ്ദിഷ്ടവര്ഗ്ഗത്തിന്റെ ആവൃത്തിയെ വിഭജിക്കുന്നതോടെ ശരിയാക്കപ്പെട്ട ആവൃത്തികള് ലഭിക്കുന്നു.
എന്നതു മുഖേന, അനുയോജ്യമായ പൊരുത്തപ്പെടൂത്തല് ഘടകത്തെക്കൊണ്ട് നിര്ദ്ദിഷ്ടവര്ഗ്ഗത്തിന്റെ ആവൃത്തിയെ വിഭജിക്കുന്നതോടെ ശരിയാക്കപ്പെട്ട ആവൃത്തികള് ലഭിക്കുന്നു.
| Table 14.11 | ||
|---|---|---|
| മാർക്കുകൾ | വിദ്യാർത്ഥികളുടെ എണ്ണം | |
| 10 – 15 | 7 | |
| 15 – 20 | 19 | |
| 20 – 25 | 27 | |
| 25 – 30 | 15 | |
| 30 – 40 | 12 | |
| 40 – 60 | 12 | |
| 60 – 80 | 8 | |
| Table 14.12 | |
|---|---|
| മാർക്കുകൾ | വിദ്യാർത്ഥികളുടെ എണ്ണം |
| 10 – 15 | 7 |
| 15 – 20 | 19 | 20 – 25 | 27 |
| 25 – 30 | 15 |
| 30 – 35 | 6 |
| 35 – 40 | 6 |
| 40 – 45 | 3 |
| 45 – 50 | 3 |
| 50 – 55 | 3 |
| 55 – 60 | 3 |
| 60 – 65 | 2 |
| 65 – 70 | 2 |
| 70 – 75 | 2 |
| 75 – 80 | 2 |
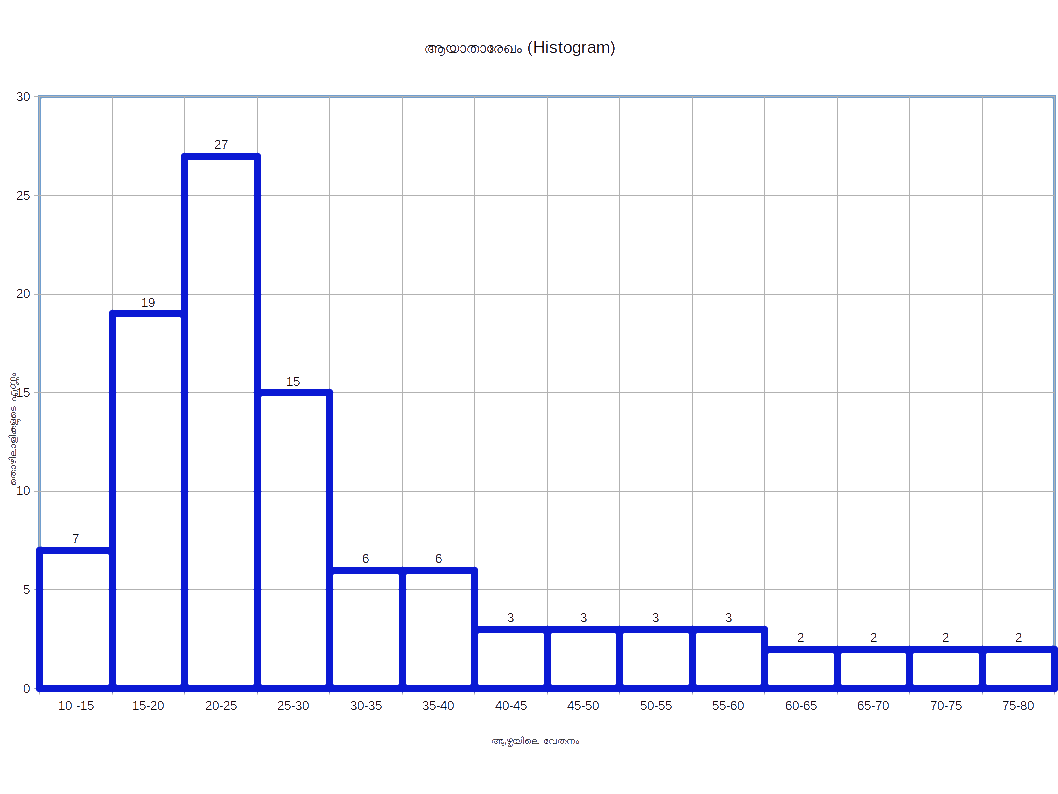
മധ്യ സംഖ്യകള് മാത്രം തരുമ്പോള് (when only mid-values are given )
മധ്യസംഖ്യകള് (Mid-values) മാത്രം നല്കപ്പെടുമ്പോള് വിവിധ വര്ഗ്ഗങ്ങളുടെ നീചസീമകളെയും ഉച്ചസീമകളെയും ഉറപ്പുവരുത്തുകയും പിന്നീട് ഇതേ മട്ടില് ആയതാരേഖം നിര്മ്മിക്കുകയും വേണം.
| Table 14.13 | ||
|---|---|---|
| മധ്യ വിലകൾ | ആവൃത്തി | |
| 15 | 10 | |
| 25 | 24 | |
| 35 | 40 | |
| 45 | 32 | |
| 55 | 20 | |
| 65 | 14 | |
| 75 | 4 | |
| Table 14.14 | ||
|---|---|---|
| ക്ലാസ് | ആവൃത്തി | |
| 10 – 20 | 10 | |
| 20 – 30 | 24 | |
| 30 – 40 | 40 | |
| 40 – 50 | 32 | |
| 50 – 60 | 20 | |
| 60 – 70 | 14 | |
| 70 – 80 | 4 | |
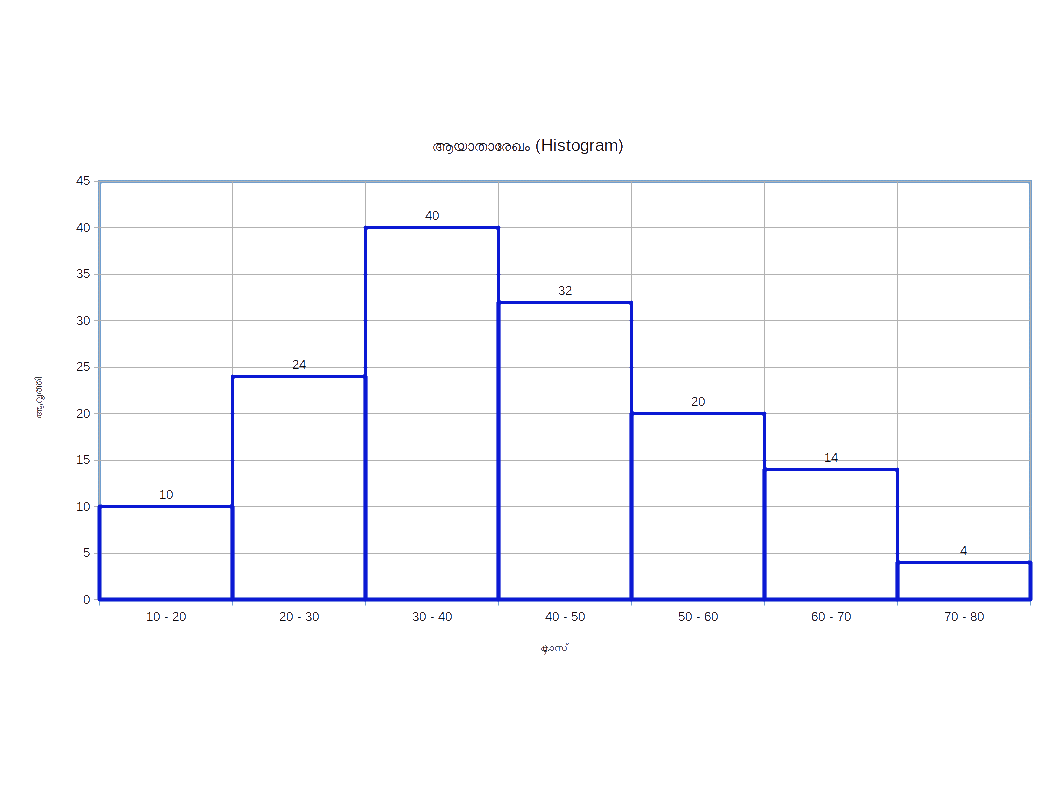
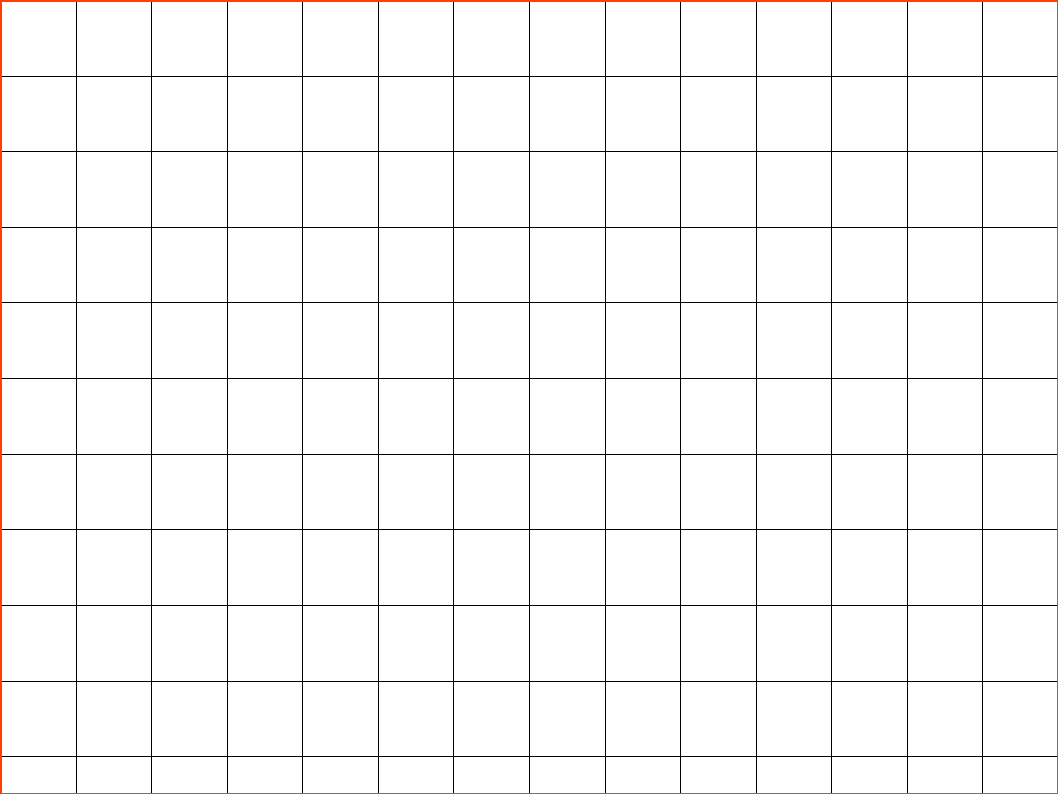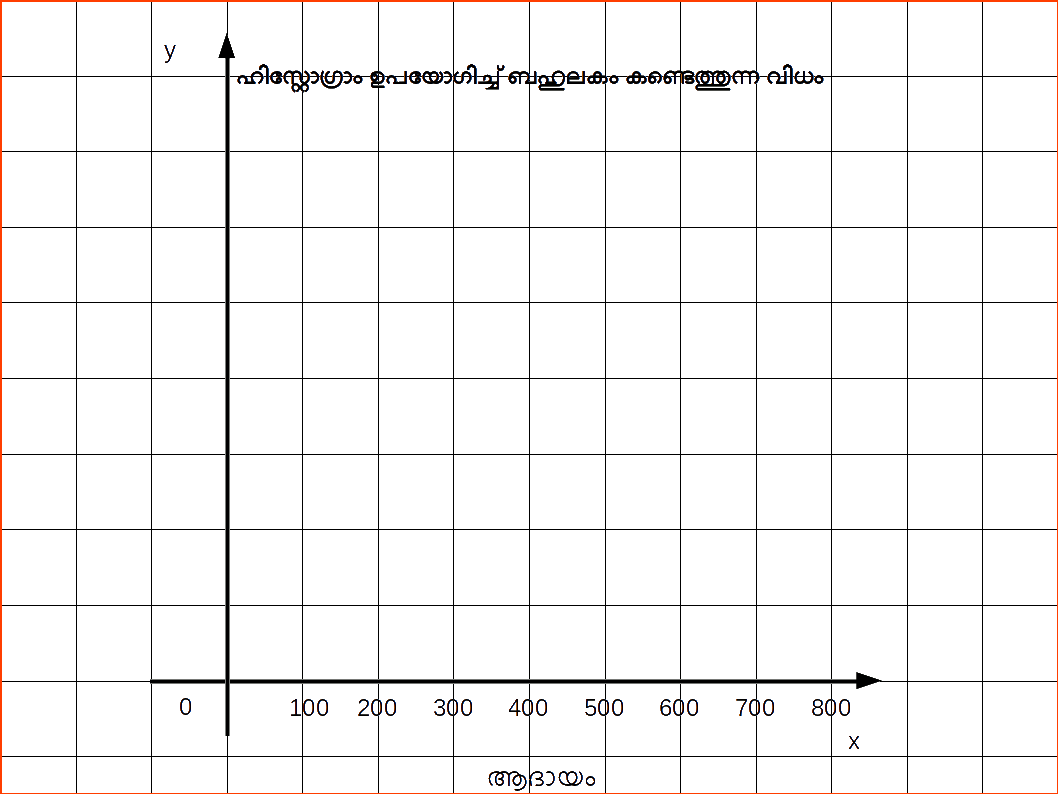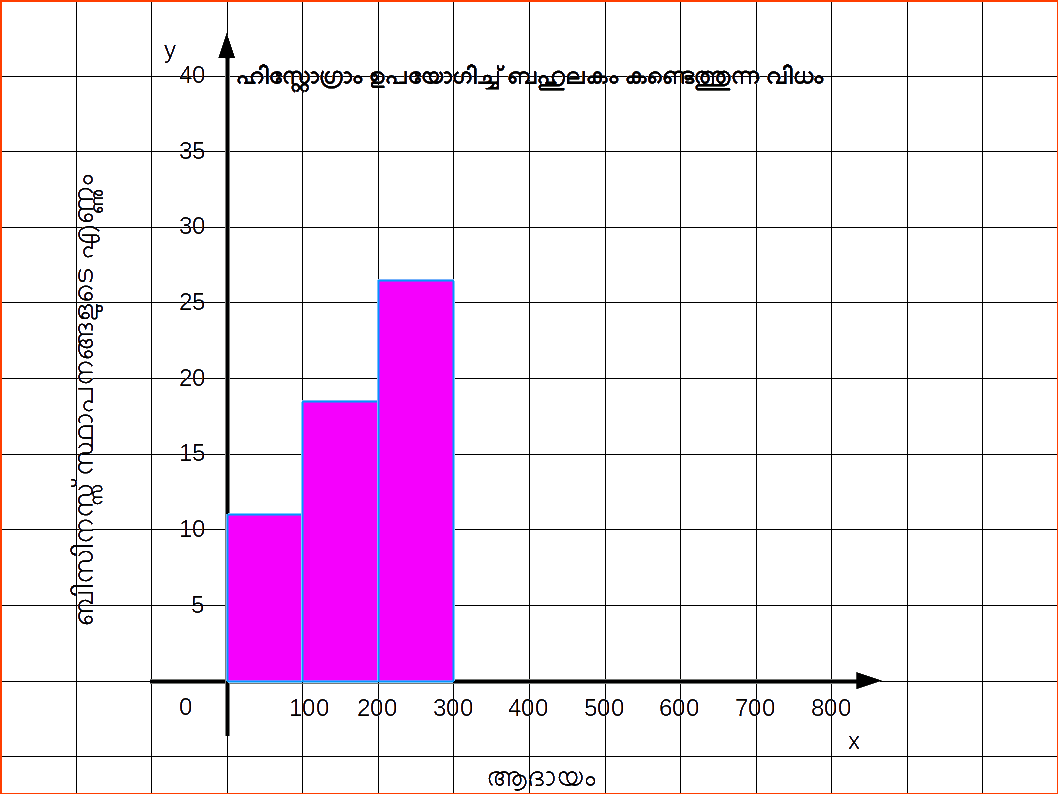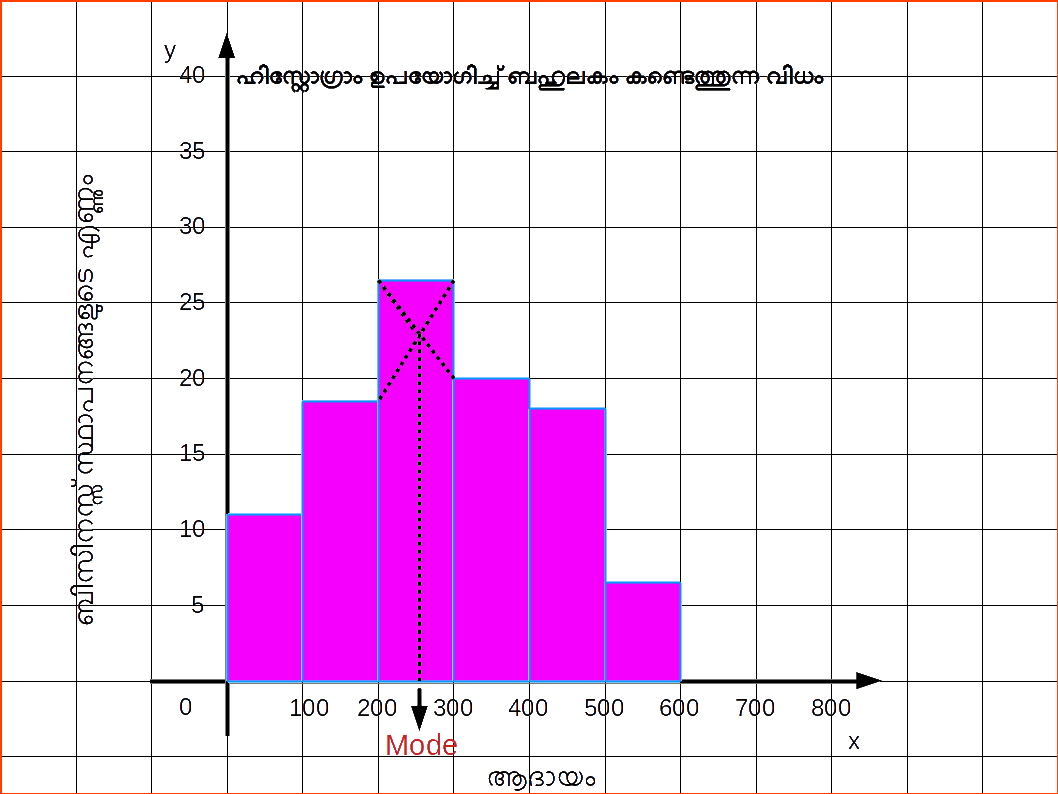
ഗ്രാഫുപയോഗിച്ച് ബഹുലകത്തെ സ്ഥാനനിര്ണ്ണയം ചെയ്യല് (Locating Mode Graphically)
പടികൾ (Steps)
- നിര്ദ്ദിഷ്ട ദത്തങ്ങളുടെ ഒരു ആയതാരേഖം വരയ്ക്കുക. രണ്ടു രേഖകള് കോണോടു കോണായി ബഹുലകവര്ഗ്ഗ ബാറിനകത്ത് (Bar) വരയ്ക്കുക.
- ബാറിന്റെ ഓരോ മൂലയില്നിന്നും തുടങ്ങി പാര്ശ്വസ്ഥ ബാറിലെ (Adjascent Bar) ഉപരിമൂലയിലേയ്ക്കു നീങ്ങുംവിധം വരയ്ക്കുക.
- പിന്നീട് കുറുകെ ഛേദിക്കുന്ന ബിന്ദുവില്നിന്ന് X അക്ഷത്തിലേയ്ക്കു ഒരു ലംബരേഖ വരയ്ക്കുക.
| Table 14.15 | ||
|---|---|---|
| ആദായം | ബിസിനസ്സ് സ്ഥാപനങ്ങളുടെ എണ്ണും | |
| 0 – 100 | 12 | |
| 100 – 200 | 18 | |
| 200 – 300 | 27 | |
| 300 – 400 | 20 | |
| 400 – 500 | 17 | |
| 500 – 600 | 6 | |
| Table 14.16 | ||
|---|---|---|
| ഉയരം | മരങ്ങളുടെ എണ്ണം | |
| 0 – 7 | 26 | |
| 7 – 14 | 31 | |
| 14 – 21 | 35 | |
| 21 – 28 | 42 | |
| 28 – 35 | 82 | |
| 35 – 42 | 71 | |
| 42 – 49 | 54 | |
| 49 – 56 | 19 | |
| Table 14.17 | ||
|---|---|---|
| മധ്യ വിലകൾ | ആവൃത്തി | |
| 5 | 10 | |
| 15 | 22 | |
| 25 | 34 | |
| 35 | 30 | |
| 45 | 20 | |
| 55 | 16 | |
| 65 | 8 | |
| Table 14.18 | ||
|---|---|---|
| ഉയരം | മരങ്ങളുടെ എണ്ണം | |
| 10 – 19 | 5 | |
| 20 – 29 | 10 | |
| 30 – 39 | 11 | |
| 40 – 49 | 9 | |
| 50 – 59 | 5 | |
| 60 – 69 | 3 | |
| Table 14.19 | |
|---|---|
| മാർക്കുകൾ | വിദ്യാർത്ഥികളുടെ എണ്ണം |
| 10 – 15 | 6 |
| 15 – 20 | 18 | 20 – 25 | 24 |
| 25 – 30 | 16 |
| 30 – 40 | 14 |
| 40 – 60 | 12 |
| 60 – 80 | 10 |
| Table 14.20 | |
|---|---|
| സാമ്പത്തികശാസ്ത്രത്തിന് ലഭിച്ച മാർക്കുകൾ | വിദ്യാർത്ഥികളുടെ എണ്ണം |
| 0 – 20 | 5 |
| 20 – 40 | 10 | 40 – 60 | 24 |
| 60 – 80 | 16 |
| 80 – 100 | 5 |
2) ആവൃത്തി ബഹുഭുജം (Frequency Polygon) ആവൃത്തി വിതരണത്തിന്റെ ഒരു ഗ്രാഫ് ആണ് ഒരാവൃത്തി ബഹുഭുജം (സന്തതം അല്ലെങ്കില് അസന്തതം).
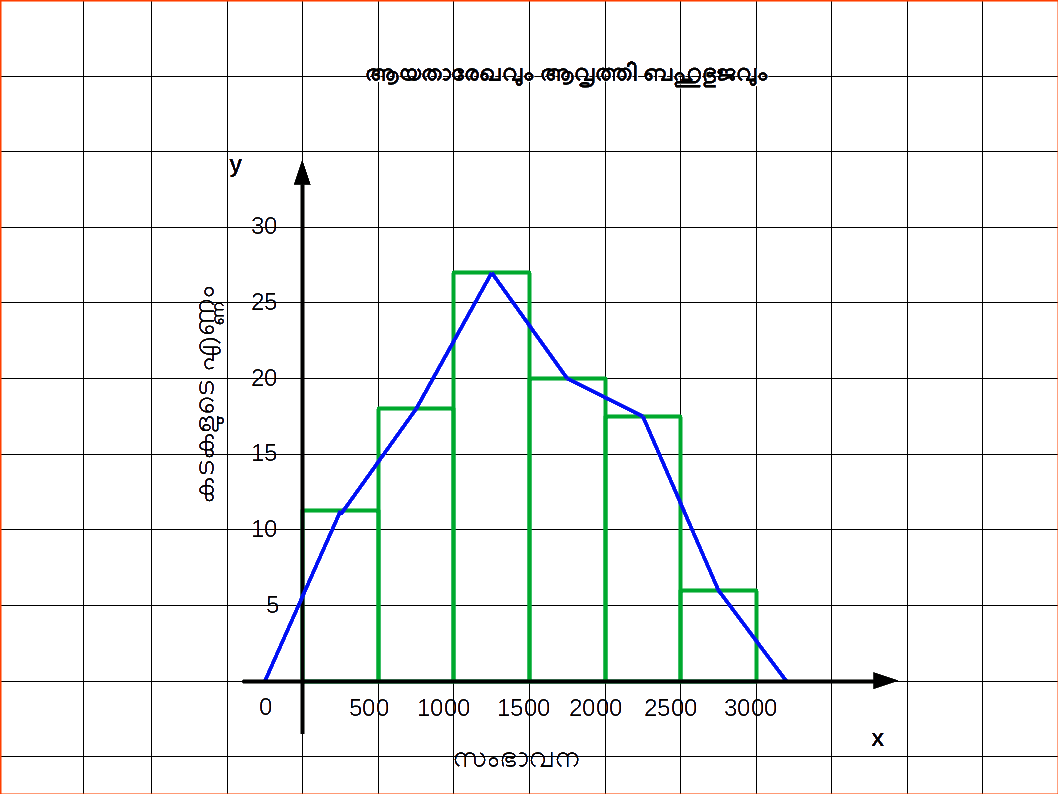
X അക്ഷത്തിന്മേല് ചരത്തിന്റെ അനുയോജ്യമായ സംഖ്യകള്ക്കു നേരെ Y അക്ഷത്തിന്മേലുള്ള ആവൃത്തികളെ കണ്ടുപിടിച്ച് അപ്രകാരം ലഭിച്ചിട്ടുള്ള സ്ഥാനങ്ങളെ നേര്വരകളാല് യോജിപ്പിച്ചുകൊണ്ടും അസന്തതശ്രേണി ലഭിക്കുന്നു. സന്തത ആവ്യൃത്തി വിതരണത്തിന്റെ കാര്യത്തില്, അതു രണ്ടുവിധത്തില് വരയ്ക്കാവുന്നതാണ്.- നിര്ദ്ദിഷ്ടദത്തങ്ങളുടെ ഒരായതാരേഖം വരയ്ക്കുക. എന്നിട്ട് ഓരോ സമകോണത്തിന്റെയും (Rectangle) ഉപരിഭാഗത്തുള്ള സമാന്തരവശത്തിലെ മധ്യസ്ഥാനങ്ങളെ തൊട്ടടുത്തുള്ളവയുമായി (adjacent) നേര്രേഖകളാല് യോജിപ്പിക്കുക. ഇപ്രകാരം ആവിഷ്കൃതമായ രൂപം ആവൃത്തി ബഹുഭൂജം എന്നറിയപ്പെടുന്നു.
- മറ്റൊരു രീതി എന്തെന്നാല്, വിവിധ വര്ഗ്ലാന്തരാളങ്ങളുടെ മധ്യസ്ഥാനങ്ങളെടുക്കുക. ഓരോ സ്ഥാനത്തിനും അനുയുക്തമായിട്ടുള്ള ആവൃത്തിയെ തുണ്ടുകളാക്കുക. എന്നിട്ട് ഈ സ്ഥാനങ്ങളെയെല്ലാം നേര്രേഖകളാല് യോജിപ്പിക്കുക. ഒരേയൊരു വ്യത്യാസം എന്തെന്നാല്, ഇവിടെ നാം ഒരു ആയതാരേഖം പണിയേണ്ടതില്ല.
| Table 14.21 | |
|---|---|
| സംഭാവന | കടകളുടെ എണ്ണം |
| 0 – 500 | 12 |
| 500 – 1000 | 18 | 1000 – 1500 | 27 |
| 1500 – 2000 | 20 |
| 2000 – 2500 | 17 |
| 2500 – 3000 | 6 |
| Table 14.22 | |
|---|---|
| സംഭാവന | കടകളുടെ എണ്ണം |
| 0 – 500 | 12 |
| 500 – 1000 | 18 | 1000 – 1500 | 27 |
| 1500 – 2000 | 20 |
| 2000 – 2500 | 17 |
| 2500 – 3000 | 6 |
| Table 14.23 | ||
|---|---|---|
| സംഭാവന | മധ്യ വിലകൾ | കടകളുടെ എണ്ണം |
| 0 – 500 | 250 | 12 |
| 500 – 1000 | 750 | 18 | 1000 – 1500 | 1250 | 27 |
| 1500 – 2000 | 1750 | 20 |
| 2000 – 2500 | 2250 | 17 |
| 2500 – 3000 | 2750 | 6 |
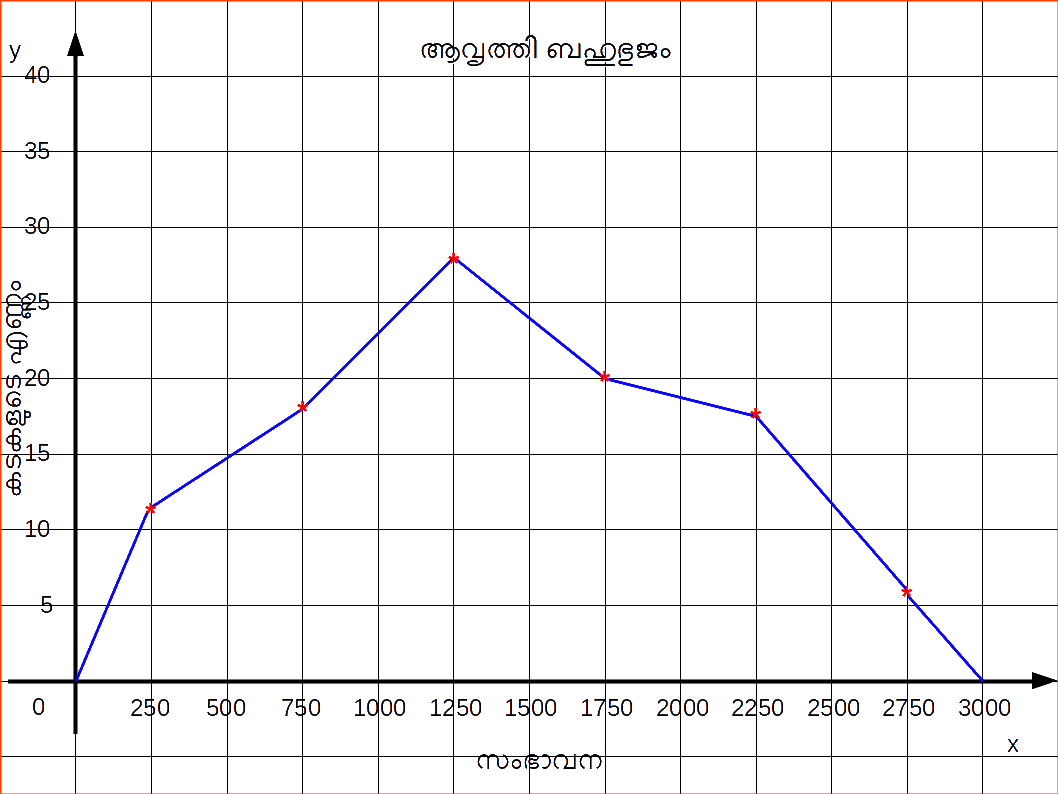 സന്തതവര്ഗ്ഗങ്ങളുടെ മധ്യസ്ഥാനങ്ങള് എന്ന നിലയില് ചരങ്ങളുടെ നിര്ദ്ദിഷ്ട സംഖ്യകളെ എടുത്തുകൊണ്ട് അസന്തത ആവൃത്തി വിതരണത്തെ പ്രതിനിധാനം ചെയ്യാനും ആയതാരേഖം ഉപയോഗിക്കപ്പെടുന്നു.
സന്തതവര്ഗ്ഗങ്ങളുടെ മധ്യസ്ഥാനങ്ങള് എന്ന നിലയില് ചരങ്ങളുടെ നിര്ദ്ദിഷ്ട സംഖ്യകളെ എടുത്തുകൊണ്ട് അസന്തത ആവൃത്തി വിതരണത്തെ പ്രതിനിധാനം ചെയ്യാനും ആയതാരേഖം ഉപയോഗിക്കപ്പെടുന്നു.
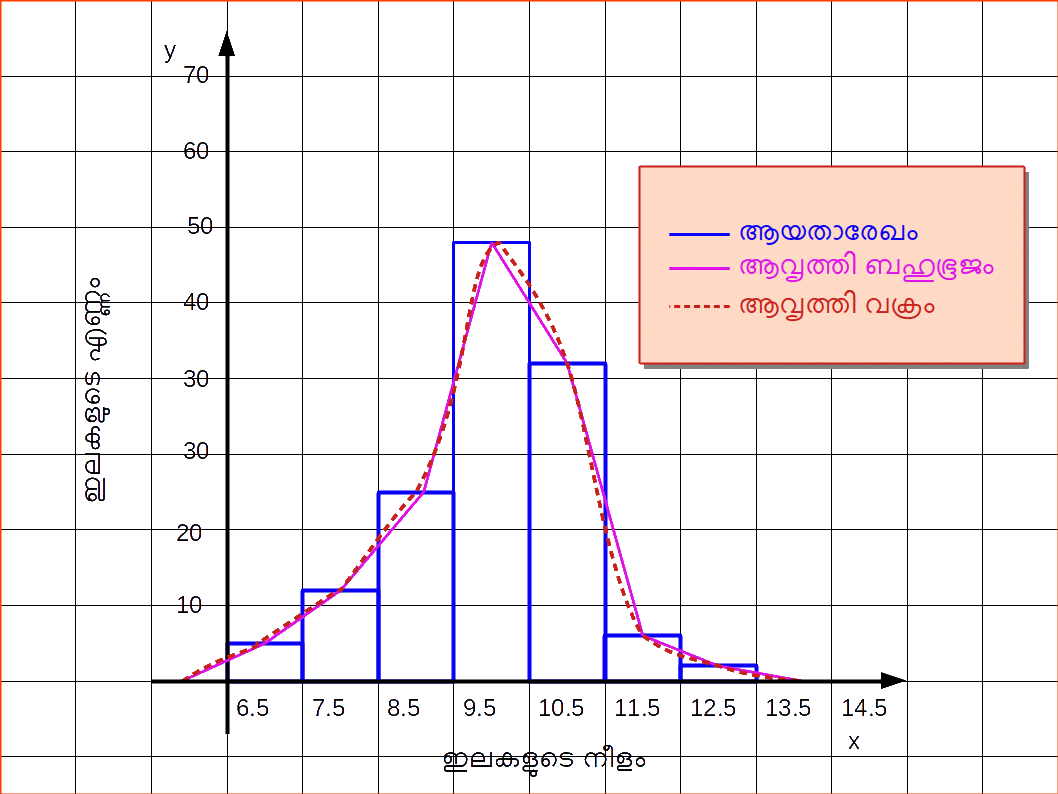
3) ആവൃത്തി വക്രം (Frequency Curve) ബഹുഭുജത്തിന്റെ (Polygon) വിവിധ സ്ഥാനങ്ങളിലൂടെ അനായാസമായി ഒരാവൃത്തിവക്രം വരയ്ക്കാവുന്നതാണ്. വക്രത്തിനു കീഴില് ഉള്ക്കൊള്ളിച്ചിട്ടുള്ള മേഖല ഏറെക്കുറെ ബഹുഭൂജത്തിന്റേതിനു തുല്യമാകുംവണ്ണം വക്രം സ്വതന്ത്രമായും ഉദാരമായും വരയ്ക്കാം. അക്ലിഷ്ടമായ ഒരു ആവൃത്തി വക്രം വരയ്ക്കുന്നതിന് ആദ്യം ബഹുഭുജം വരയ്ക്കേണ്ടുന്നതും പിന്നീടതിനെ മയപ്പെടുത്തിയെടുക്കേണ്ടുന്നതും (smoothen it out) ആവശ്യമാണ്. ആയതാരേഖം ആദ്യം നിര്മ്മിക്കാതെ തന്നെ വര്ഗ്ലാന്തരാളങ്ങളുടെ മധ്യസ്ഥാനങ്ങളില് ആവൃത്തികളെ തുണ്ടുകളാക്കിക്കൊണ്ട് ബഹുഭുജം നിര്മ്മിക്കാവുന്നതാണ്.
പൂതിയ അംശങ്ങള് തിരുകിക്കയറ്റൂന്നതിന് (interpolation) ആവൃത്തി വക്രങ്ങള് ഉപയോഗിക്കാവൂന്നതാണ്.| Table 14.24 | |
|---|---|
| ഇലകളുടെ നീളം(cm) | ഇലകളുടെ എണ്ണം |
| 6.5 – 7.5 | 5 |
| 7.5 – 8.5 | 12 | 8.5 – 9.5 | 25 |
| 9.5 – 10.5 | 48 |
| 10.5 – 11.5 | 32 |
| 11.5 – 12.5 | 6 |
| 12.5 – 13.5 | 1 |
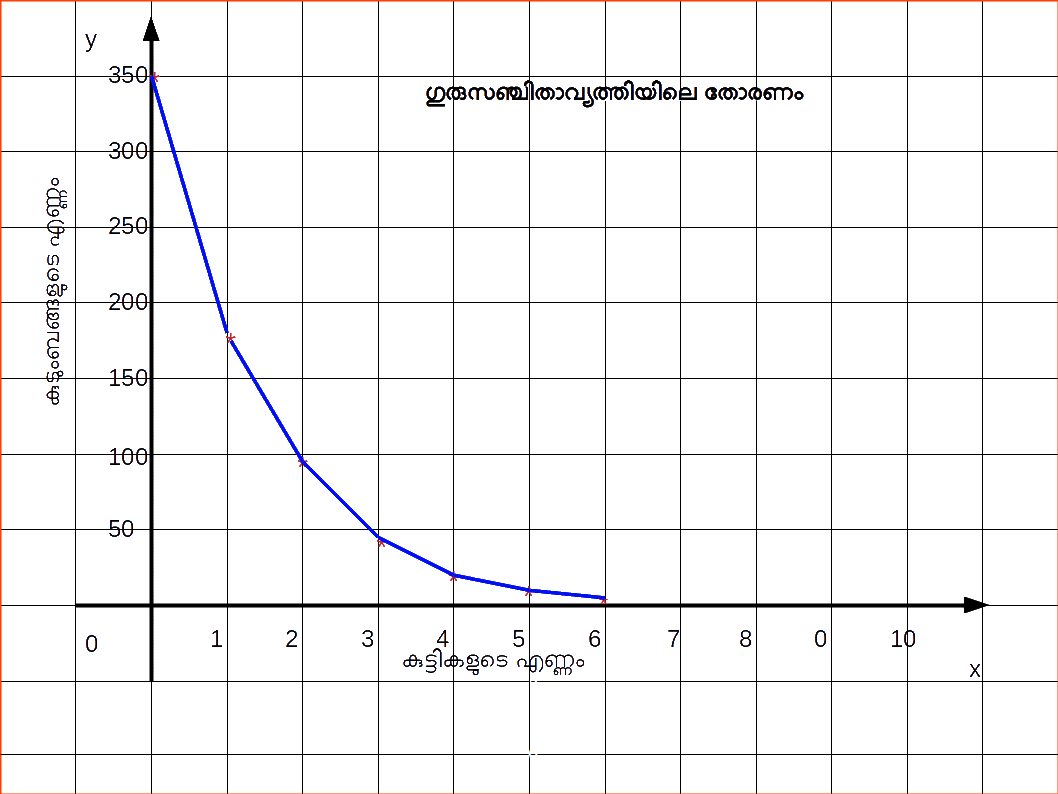
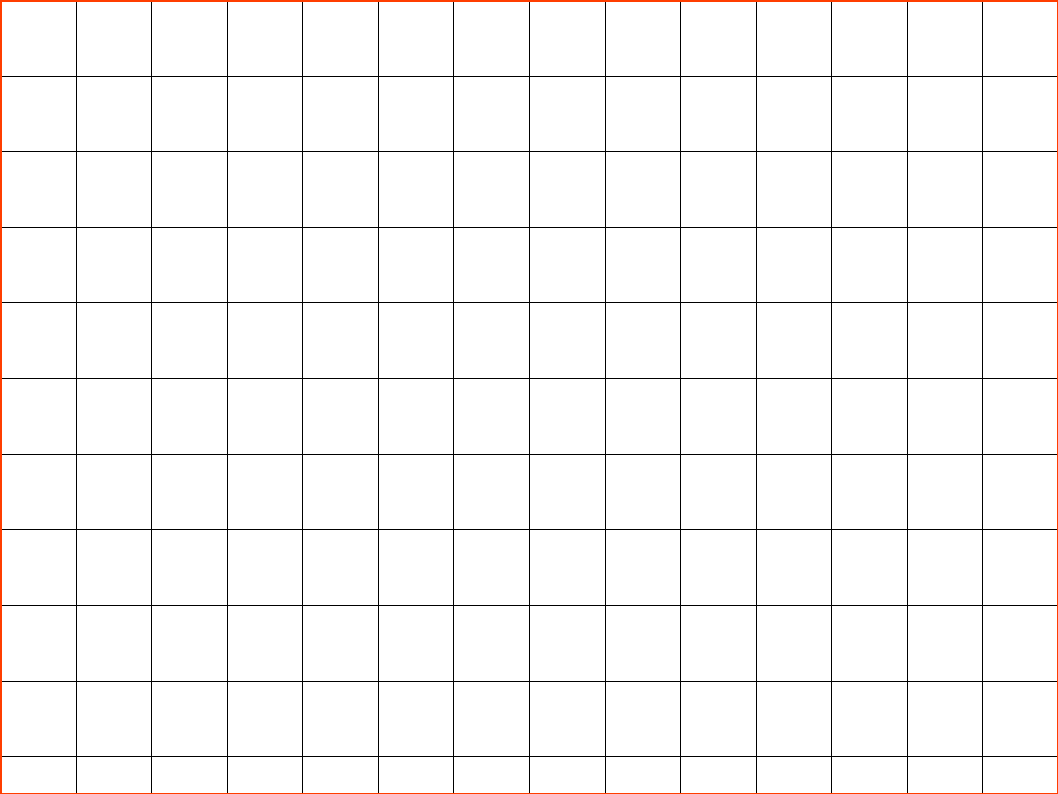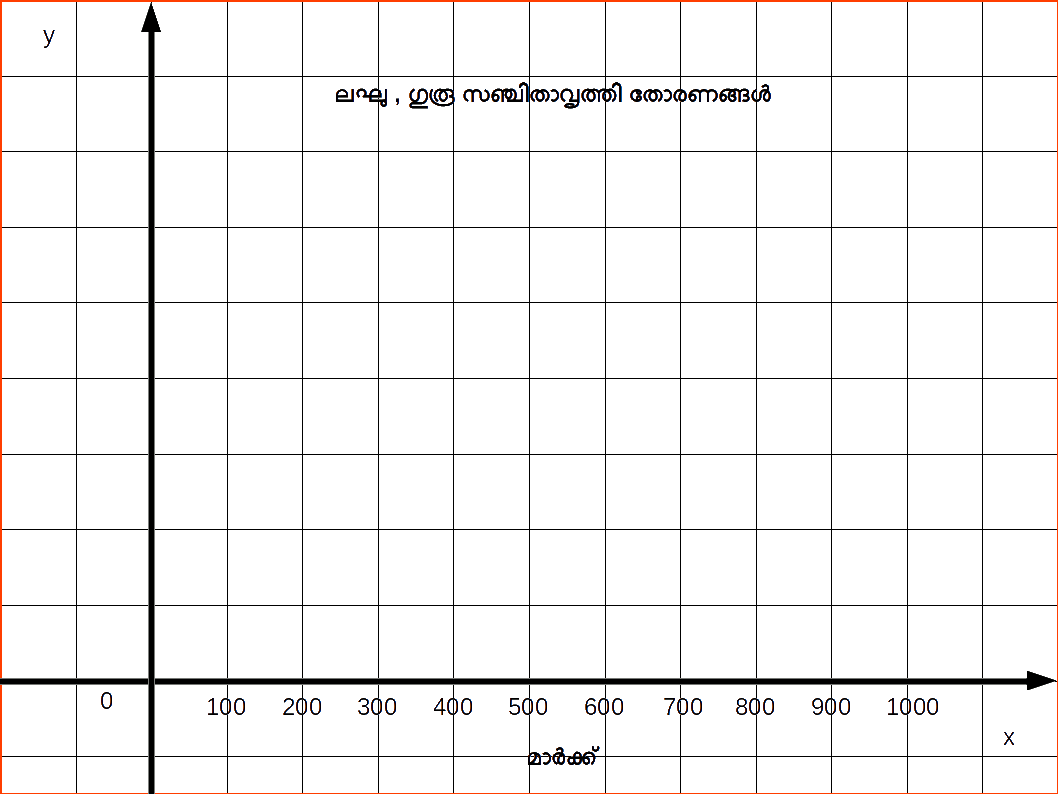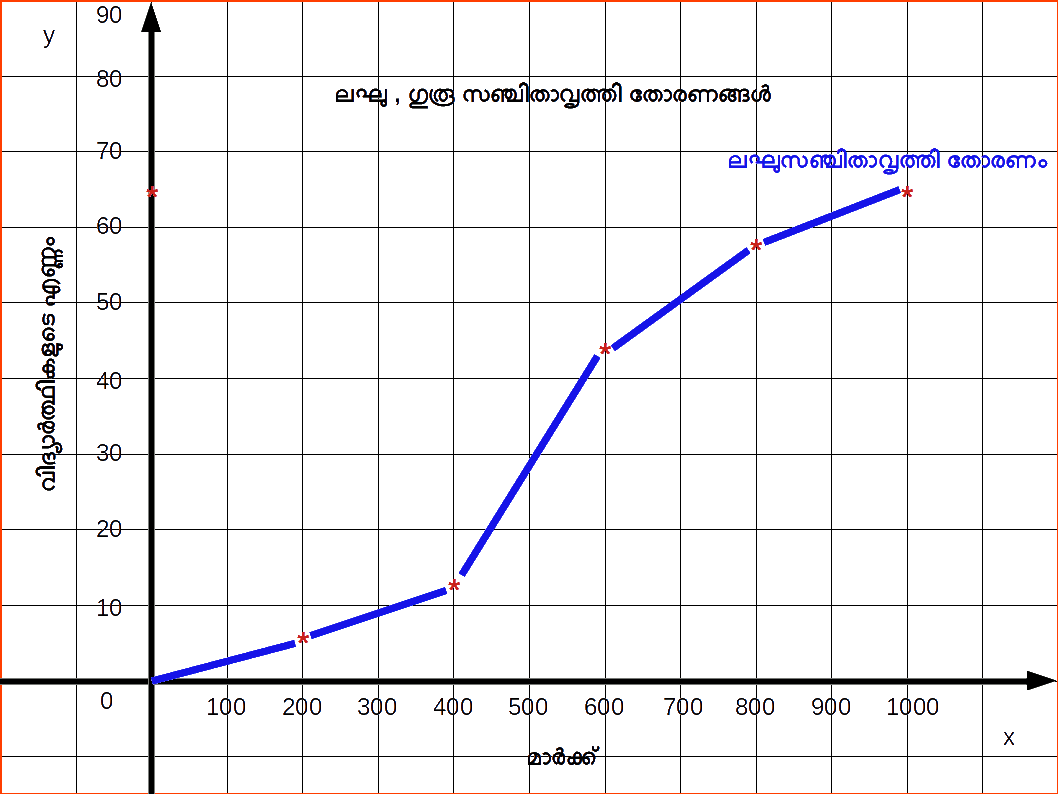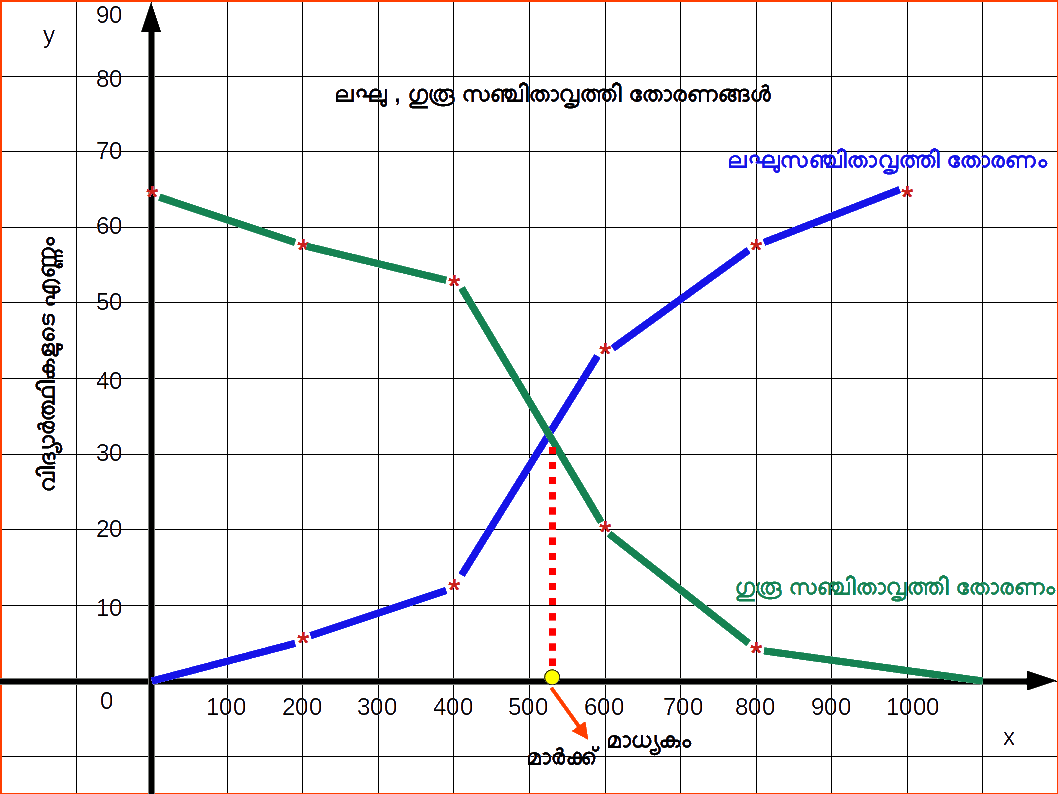
4) ഒജീവ് (Cumulative Frequency Curve or Ogives) ലഘുസഞ്ചിതാവൃത്തി (The less than method) ഗുരുസഞ്ചിതാവൃത്തി (The more than method) ലഘുസഞ്ചിതാവൃത്തി രീതിയില് നാം വര്ഗ്ഗങ്ങളുടെ ഉച്ഛസീമയില് തുടങ്ങുകയും ആവ്യത്തികളെ കൂട്ടിച്ചേര്ത്തുകൊണ്ടു നീങ്ങുകയും ചെയ്യുന്നു. ഈ ആവൃത്തികള് തുണ്ടുകളാക്കുപ്പെടുമ്പോള് നമുക്കു ഉയര്ന്നുവരുന്ന വക്രം (Rising curve) കിട്ടുന്നു.
ഗുരുസഞ്ചിതാവൃത്തി രീതിയില് നാം വര്ഗ്ഗങ്ങളുടെ നീചസീമയില് ആരംഭിക്കുകയും ആവൃത്തികളില് നിന്ന് ഓരോ വര്ഗ്ഗത്തിന്റെ ആവ്യത്തികളെ കുറച്ചുകൊണ്ടു വരികയും ചെയ്യുന്നു. ഈ ആവൃത്തികളെ തുണ്ടുകളാക്കുമ്പോള് നമുക്കു താഴ്ന്നുവരുന്ന വക്രം (Declining curve) കിട്ടുന്നു. ഈ രണ്ടൂ സഞ്ചിതശ്രേണികള്ക്കുമായി വരയ്ക്കപ്പെട്ട മയപ്പെട്ട (smothed) ആവ്യത്തിവ്രകങ്ങളാണ് സഞ്ചിതാവൃത്തി വ്രക്രങ്ങള് അഥവാ തോരണങ്ങ. രണ്ടു വക്രങ്ങളും ഏതു ബിന്ദുവില് വച്ചാണോ പരസ്ത്രരം ഛേദിക്കുന്നത് ആ ബിന്ദു മാധ്യകത്തിന്റെ (median) സംഖ്യ നല്കുന്നു. ഒരു ചരത്തിന്റെ ചതുര്ത്ഥകങ്ങടെയും (Quartiles) ദശമകങ്ങളുടെയയും (Deciles) ശതമകങ്ങളുടെയും (Percentiles) സംഖ്യകള് കണ്ടൂപിടിക്കുന്നതിന് തോരണങ്ങള് ഉപയോഗിക്കാവുന്നതാണ്.| Table 14.25 | |
|---|---|
| കുട്ടികളുടെ എണ്ണം | കുടുംബങ്ങളുടെ എണ്ണം |
| 1 | 171 |
| 2 | 82 | 3 | 50 |
| 4 | 25 |
| 5 | 13 |
| 6 | 7 |
| 7 | 2 |
| Table 14.26 | |
|---|---|
| കുട്ടികളുടെ എണ്ണം | കുടുംബങ്ങളുടെ എണ്ണം |
| 0 – 1 | 171 |
| 1 – 2 | 82 | 2 – 3 | 50 |
| 3 – 4 | 25 |
| 4 – 5 | 13 |
| 5 – 6 | 7 |
| 6 – 7 | 2 |
| Table 14.27 | |
|---|---|
| കുട്ടികളുടെ എണ്ണം | കുടുംബങ്ങളുടെ എണ്ണം |
| 1 ൽ താഴെ | 171 |
| ” ” 2 | 253 |
| ” ” 3 | 303 |
| ” ” 4 | 328 |
| ” ” 5 | 341 |
| ” ” 6 | 348 |
| ” ” 7 | 350 |
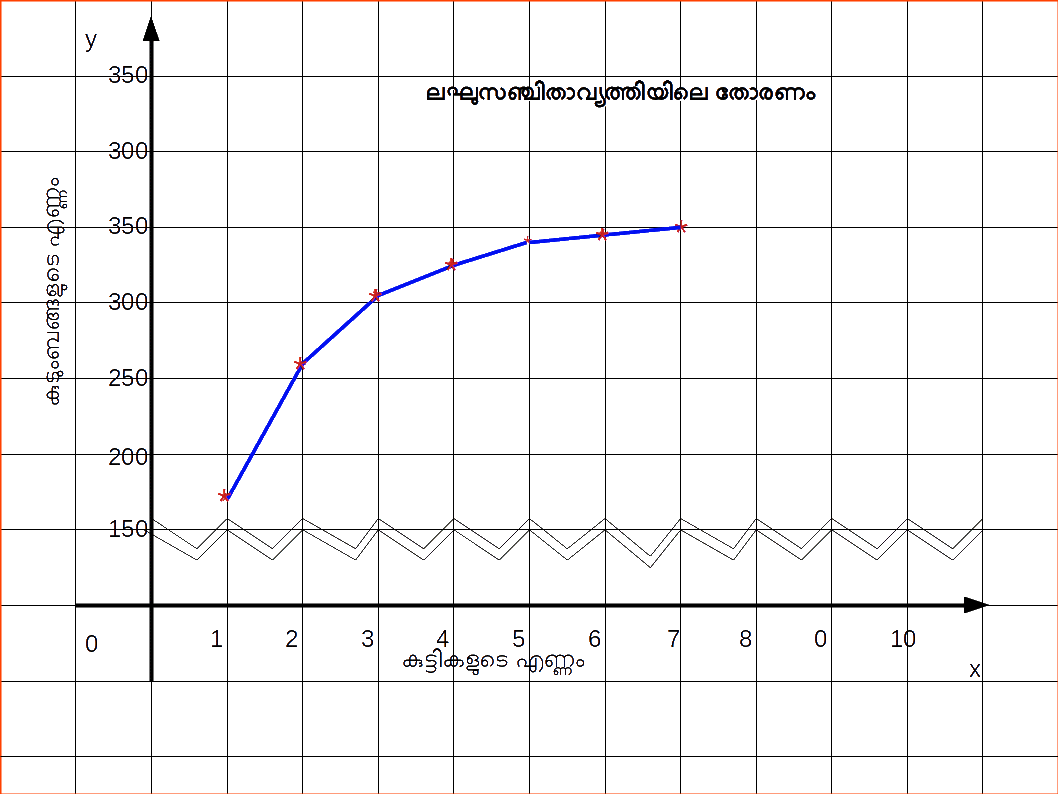 ഗുരുസഞ്ചിത ശ്രേണി
ഗുരുസഞ്ചിത ശ്രേണി
| Table 14.28 | |
|---|---|
| Number of children | Number of families |
| 0 ഉം അധികവും | 350 |
| 1 ” “ | 179 |
| 2 ” “ | 97 |
| 3 ” “ | 47 |
| 4 ” “ | 22 |
| 5 ” “ | 9 |
| 6 ” “ | 2 |
ഗ്രാഫൂപയോഗിച്ച് മാധ്യകത്തിന്റെ നിര്ണയം (Determination of Median Graphically)
രണ്ടു സഞ്ചിത ആവൃത്തി വക്രങ്ങൾ വരച്ചുകൊണ്ടും നമുക്കു മൂല്യം നിര്ണ്ണയിക്കാവുന്നതാണ്. ഒന്ന് ലഘുസഞ്ചിത രീതിയും (Less than method) മറ്റൊന്ന് ഗുരുസഞ്ചിത രീതിയും (More than method) ആണ്. ഈ രണ്ടു വക്രങ്ങളും സന്ധിക്കുന്ന ബിന്ദുവില്നിന്ന് X അക്ഷത്തില് ഒരു ലംബം വരയ്ക്കുക. Y അക്ഷത്തില് അതു സന്ധിക്കുന്ന ബിന്ദുവാണ് മാധ്യകും.
| Table 14.29 | ||
|---|---|---|
| Mid-value | Less than cumulative frequency | More than cumulative frequency |
| 0 | — | 83 |
| 5 | 2 | 81 | 10 | 7 | 76 |
| 15 | 13 | 70 |
| 20 | 21 | 62 |
| 25 | 34 | 49 |
| 30 | 51 | 32 |
| 35 | 62 | 21 |
| 40 | 70 | 13 |
| 45 | 75 | 8 |
| 50 | 79 | 4 |
| 55 | 82 | 1 |
| 60 | 83 | — |
The less than and more than ogives drawn together for the data is given in the below figure.
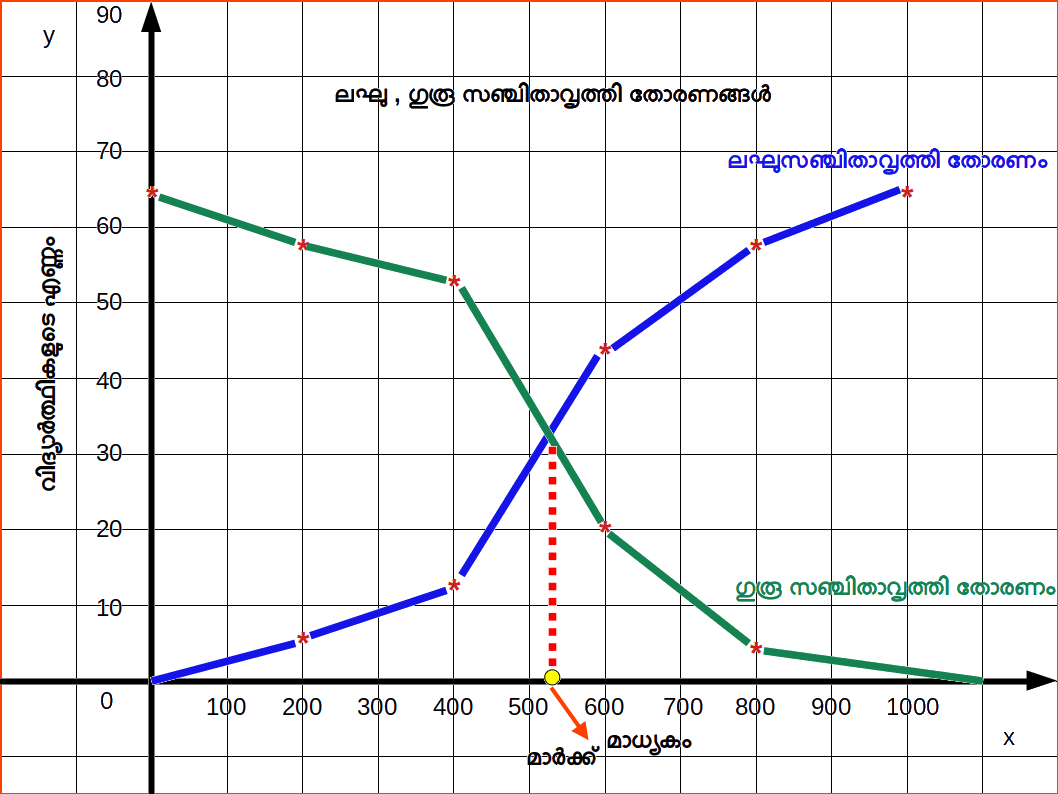
Method of finding Median from Ogives
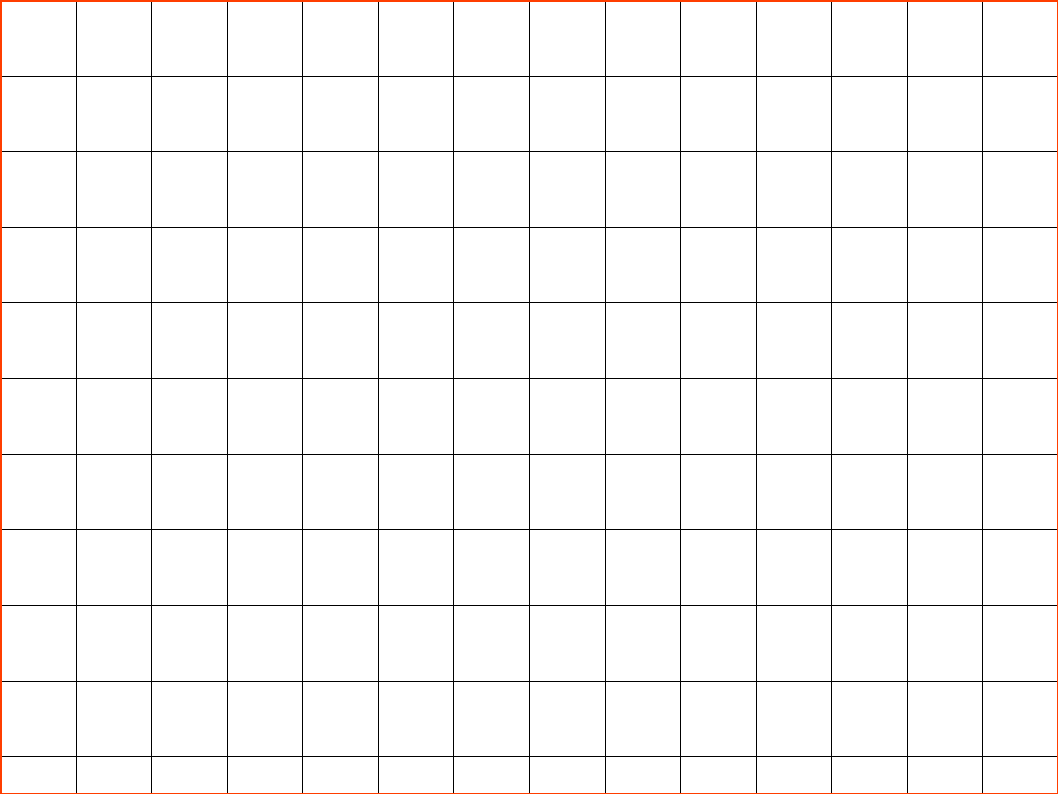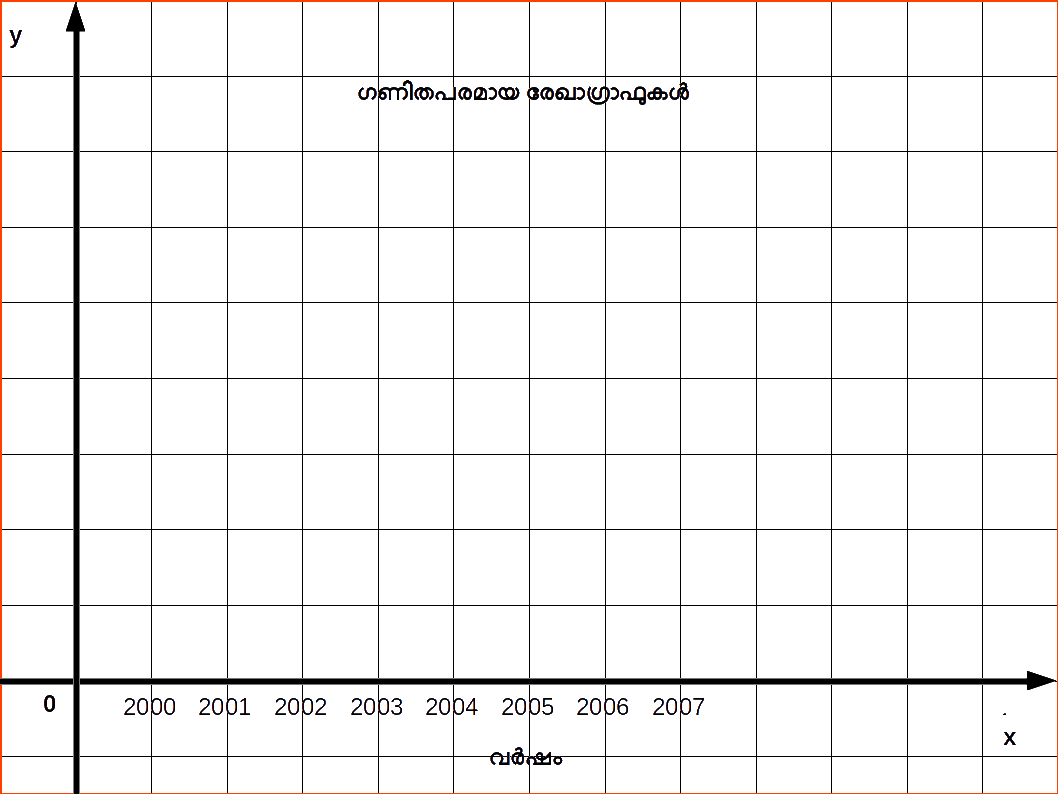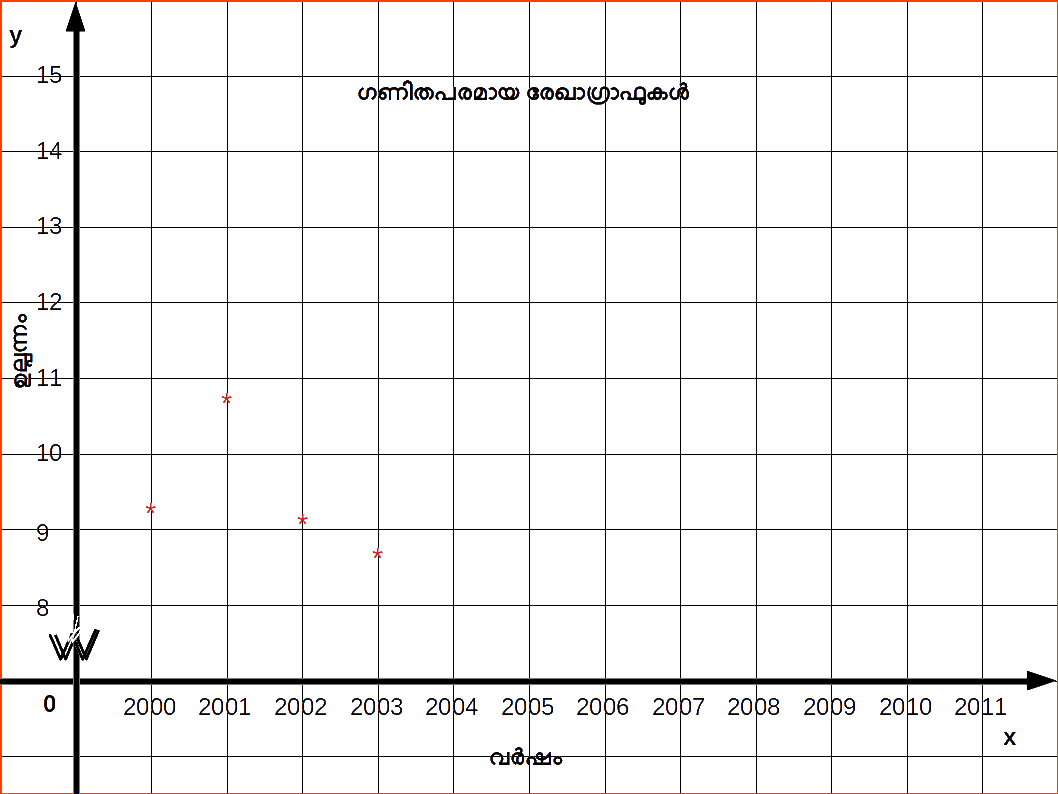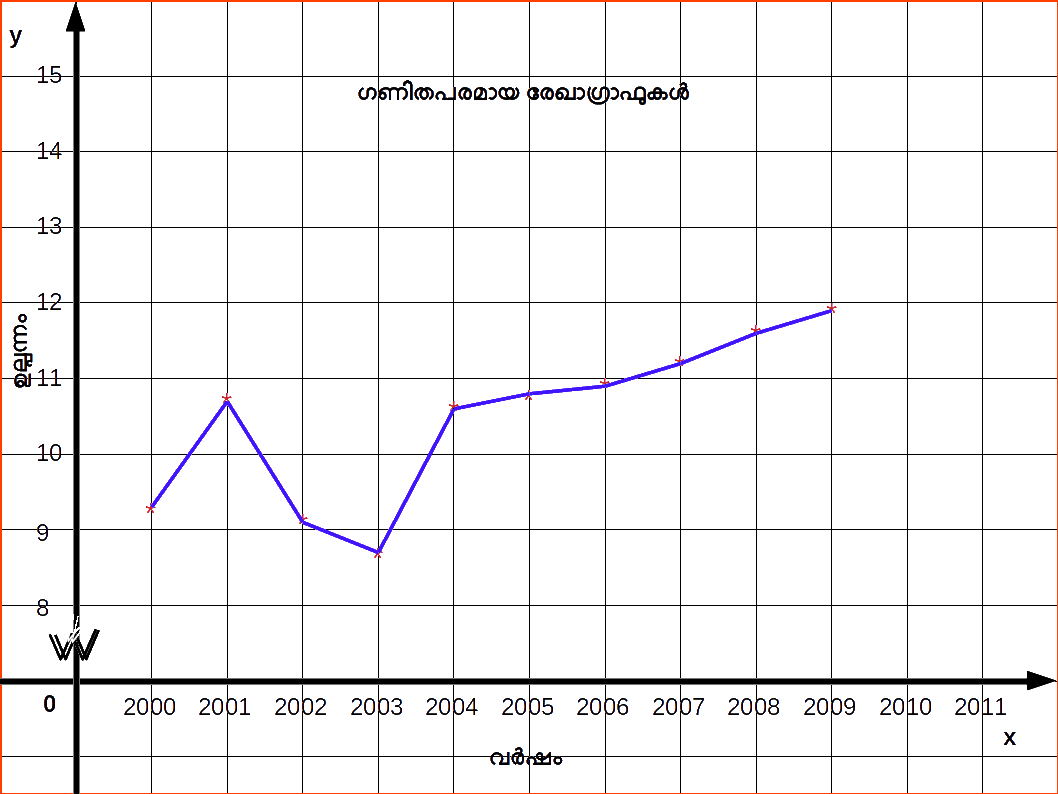
III. ഗണിതപരമായ രേഖാഗ്രാഫുകള് (ടൈം സീരീസ് ഗ്രാഫ്) (Arithmetic Line graph / Time Series Graph) സാംഖ്യിക ദത്തങ്ങളെ ഒരു കാലയളവിന്റെ അടിസ്ഥാനത്തില് ക്രമീകരിക്കുന്ന രീതിക്കാണ് ടൈം സീരീസ് എന്ന് വിളിക്കുന്നത്. അപ്പോള് ടൈം സീരീസില് ഒരു ചരം (variable) സമയമായിരിക്കും. ടൈം സീരീസ് ഗ്രാഫില് കൊല്ലം, മാസം എന്ന കണക്കില് സമയ യുണിറ്റ് X അക്ഷത്തിലും ചരത്തിന്റെ മൂല്യം (value) Y അക്ഷത്തിലൂം ആയി എടുക്കുന്നു.
| Table 14.30 | |
|---|---|
| Year | Production |
| 2000 | 9.54 |
| 2001 | 10.83 |
| 2002 | 9.12 |
| 2003 | 8.85 |
| 2004 | 10.62 |
| 2005 | 10.85 |
| 2006 | 10.95 |
| 2007 | 11.35 |
| 2008 | 11.65 |
| 2009 | 11.98 |
ഇവിടെ ആശ്രിത വേരിയബിൾ ഉരുക്ക് ഉൽപാദനമാണ്. അതിനാൽ ഇത് y-അക്ഷത്തിലും സമയപരിധി x-അക്ഷത്തിലും അടയാളപ്പെടുത്തിയേക്കാം. മുകളിലുള്ള ഡാറ്റയുടെ ഗണിതരേഖ ഗ്രാഫ് ചുവടെയുള്ള ഡയഗ്രാമിൽ നൽകിയിരിക്കുന്നു.
![]()

