Plus Two Economics – Chapter 2: Note in Malayalam

ഉപഭോക്തൃ പെരുമാറ്റ സിദ്ധാന്തങ്ങൾ

Plus Two Economics

ഉപഭോക്താക്കള്‍ തങ്ങളുടെ ആവശ്യങ്ങളെ തൃപ്തിപ്പെടുത്തുന്നതിനുവേണ്ടി സാധനങ്ങളും സേവനങ്ങളും ഉപഭോഗം ചെയ്യുന്നു. ഉപഭോക്താവിന്റെ ആവശ്യങ്ങളെ തൃപ്തിപ്പെടുത്താനുള്ള സാധനങ്ങളുടേയോ സേവനങ്ങളുടേയോ കഴിവിനെ ഉപയോഗയോഗ്യത (Utility) എന്നു പറയുന്നു. ഒരു കമ്പോളത്തില്‍ യൂട്ടിലിറ്റിയുടെ അളക്കൽ, ഉപഭോക്താവ്‌ സന്തുലനാവസ്ഥ പ്രാപിക്കുന്ന പ്രക്രിയ എന്നിവയെക്കുറിച്ചൊക്കെ വിശദമാക്കുന്നതിന്‌ ഇക്കണോമിക്സില്‍ വ്യത്യസ്തങ്ങളായ സിദ്ധാന്തങ്ങളുണ്ട്‌. അവയില്‍ പ്രധാനപ്പെട്ടവ താഴെ കൊടുക്കുന്നു.

കാർഡിനൽ യൂട്ടിലിറ്റി സമീപനം – ആൽഫ്രഡ് മാർഷൽ
ഈ സിദ്ധാന്തമനുസരിച്ച്‌ യൂട്ടിലിറ്റിയെ കാര്‍ഡിനലായി അളക്കാന്‍ കഴിയുമെന്ന്‌ മാര്‍ഷല്‍ കരുതുന്നു.

ഓർഡിനൽ സമീപനം – ജെ.ആര്‍. ഹിക്‌സ്‌
ഈ സിദ്ധാന്തപ്രകാരം യൂട്ടിലിറ്റിയെ കാര്‍ഡിനല്‍ ആയി അളക്കാന്‍ കഴിയില്ല. പക്ഷേ, റാങ്കുകളാക്കാന്‍ കഴിയും. ഈ അനാലിസിസ്‌ നിസ്സംഗതാ വക്ര സമീപനം (Indifference Curve Analysis) എന്ന പേരിലും അറിയപ്പെടുന്നു.

റിവീൽഡ് പ്രിഫറൻസ് സമീപനം – പോള്‍ എ. സാമുവെല്‍സണ്‍
ഈ അദ്ധ്യായത്തില്‍ നാം ഓര്‍ഡിനല്‍ യൂട്ടിലിറ്റി അനാലിസിസിനെക്കുറിച്ചാണ്‌ പഠിക്കുന്നത്‌.

ഉപഭോഗബണ്ടില്‍ ( Consumption Bundle)
ഒരു ഉപഭോക്താവ്‌ രണ്ടു സാധനങ്ങള്‍ മാത്രം വാങ്ങുന്നു എന്നു കരുതുക. സാധനം-1, സാധനം 2 എന്നിവയാണ്‌ അവയെന്നും കരുതുക. ഉപഭോക്താക്കൾ രണ്ടു സാധനങ്ങള്‍ മാത്രം വാങ്ങുന്ന അവസ്ഥയില്‍ സാധനങ്ങളുടെ അളവുകളുടെ സംയോഗത്തെ ഉപഭോഗബണ്ടില്‍ (Consumption Bundle) എന്നു പറയാം.
വിഷകലനത്തിനായി ഇവിടെ രണ്ട് സാധനങ്ങൾ മാത്രമെ ഉള്ളുവെന്ന് കരുതുക. അവ സാധനം 1 ഉം സാധനം 2 ഉം ആണെന്ന് സങ്കൽപിക്കുക. സാധനം 1 ന്റെ ഏതാനം ചില യൂണിറ്റിനെ X₁ എന്നും സാധനം 2 ന്റെ ഏതാനം ചില യൂണിറ്റിനെ X₂ എന്നും സൂചിപ്പിക്കുകയാണങ്കിൽ (X₁ , X₂ ) നെ ഉപഭോഗ ബണ്ടിൽ എന്ന് വിളിക്കാം. x₁ ഉം x₂ ഉം പുജ്യമൊ പോസിറ്റീവോ ആകാവുന്നതാണ്.

ഉപഭോക്താവിന്റെ ബജറ്റ്‌( Consumer’s Budget)
ഉപഭോക്താവിന് ലഭ്യമായിട്ടുള്ള ഉപഭോഗ ബണ്ടിലുകൾ സാധനങ്ങളുടെ വിലയെയും വരുമാനത്തെയും ആശ്രയിച്ചിരിക്കുന്നു.

‘ഉപഭോക്താവിന്റെ ഇഷ്ടാനുസരണം ചെലവഴിക്കാൻ തന്റെ കൈവശം ലഭ്യമായിട്ടുള്ള വരുമാനത്തെ ഉപഭോക്താവിന്റെ ബജറ്റ് എന്ന് പറയുന്നു.’

ഒരു ഉദാഹരണം കാണുക. നിങ്ങളുടെ കയ്യില്‍ 100 രൂപയുണ്ടെന്നിരിക്കട്ടെ. അതുപയോഗിച്ച്‌ നിങ്ങള്‍ ചോക്കലേറ്റും വളകളും വാങ്ങാനാഗ്രഹിക്കുന്നു. ഈ സാധനങ്ങളുടെ വിലകളും അറിയാം. ചോക്കലേറ്റിന്റെ വില 10 ഉം വളകളുടെ വില 20ഉം ആണ്‌. അപ്പോള്‍ തീര്‍ച്ചയായും നമുക്ക്‌ വ്യത്യസ്തങ്ങളായ ഉപഭോഗബണ്ടിലൂകള്‍ ഉണ്ടാക്കാന്‍ കഴിയും. അതായത്‌, 2 യൂണിറ്റ്‌ ചോക്കലേറ്റും 4 യൂണിറ്റ്‌ വളകളും. ഇതിന്റെ ഉപഭോഗ ബണ്ടില്‍ (2, 4) ആയിരിക്കും. (10, 0) എന്നത്‌ മറ്റൊരു ഉപഭോഗബണ്ടിലാണ്‌. ഇവിടെ താഴെ തന്നിരിക്കുന്ന വസ്തുതകള്‍ ദര്‍ശിക്കാനാവും.
ഉപഭോക്താവിന്റെ ബജറ്റ്‌ എന്നത്‌ 100 രൂപയാണ്‌.
സാധനങ്ങളുടെ വില യഥാക്രമം 10, 20 എന്നിങ്ങനെയാണ്‌.
ഉപഭോക്തൃ ബണ്ടില്‍ ഉണ്ടാക്കുന്നതിന്‌ വാങ്ങാനുദ്ദേശിക്കുന്ന സാധനത്തിന്റെ വില, ഉപഭോക്താവിന്റെ ബജറ്റ്‌ തുടങ്ങിയ വിവരങ്ങള്‍ ആവശ്യമാണ്‌.
സാധനങ്ങളും സേവനങ്ങളും വാങ്ങുന്നതിന്‌ ഒരു ഉപഭോക്താവിന്‌ ലഭ്യമായിട്ടുള്ള വരുമാനമാണ്‌ ഉപഭോക്തൃബജറ്റ്‌ കൊണ്ട്‌ അര്‍ത്ഥമാക്കുന്നത്‌ . വില തന്നിട്ടുണ്ടെങ്കില്‍, സാധനങ്ങളും സേവനങ്ങളും വാങ്ങാനുള്ള ഉപഭോക്താവിന്റെ ആഗ്രഹത്തിന്‌ ബജറ്റ്‌ ഉയര്‍ന്ന ഒരു അതിര്‍വരമ്പ് സൃഷ്ടിക്കുന്നു. ഇവിടെ, നമുക്ക്‌ (4, 5) എന്ന ബണ്ടില്‍ വാങ്ങാന്‍ കഴിയില്ല. ഈ ബണ്ടില്‍ വാങ്ങണമെന്നുണ്ടെങ്കില്‍ ഉപഭോക്താവിന്‌ 140 രൂപ ചെലവഴിക്കേണ്ടതായി വരും. ഇത്‌ അയാള്‍ക്ക്‌ ല്യമായ ബജറ്റിനും മീതെയാണ്‌. അതുകൊണ്ടുതന്നെ അതു സാദ്ധ്യവുമല്ല.
ഉപഭോക്താവിന്റെ ബജറ്റും, സാധനങ്ങളുടെ വിലയും തന്നിരുന്നാല്‍, ഉപഭോക്താവിന്‌ തന്റെ വരുമാനത്തിനു തുല്യമോ അല്ലെങ്കില്‍ അതിനു താഴെയോ വില വരുന്ന ഉപഭോഗബണ്ടിലുകള്‍ വാങ്ങാവുന്നതാണ്‌.

ബജറ്റ്‌ സെറ്റ്‌ (Budget Set)
ഉപഭോക്താവിന്റെ വരുമാനവും സാധനങ്ങളുടെ വിലയും തന്നിരുന്നാൽ ഉപഭോക്താവിന്‌ വാങ്ങാ൯ കഴിയുന്ന ഉപഭോഗ ബണ്ടിലുകളുടെ സമുഹത്തെ ബജറ്റ്സെറ്റ്‌ എന്നുപഠയുന്നു. ബജറ്റ്സെറ്റില്‍ ഉപഭോക്താവിന്റെ വരുമാനം പുര്‍ണ്ണമായോ അതില്‍ താഴെയോ ചെലവഴിക്കപ്പെടുന്ന ഉപഭോഗബണ്ടിലുകള്‍ മാത്രമാണ് ഉൾപ്പെടുക.
ഒരു ഉപഭോക്താവിന്റെ വരുമാനം 12 രൂപ, സാധനം 1 ന്റെ വില 4 രൂപ, സാധനം 2 ന്റെ വില 2 രൂപ. ബജറ്റ്‌ സെറ്റ്‌ രൂപികരിച്ചു നോക്കാം. ഇവിടെ സാധനങ്ങൾ വിഭജിക്കാതെ വേണം ബജറ്റ് സെറ്റ് നിർമ്മിക്കാൻ .
ഇവിടെ ഉപഭോഗ ബണ്ടിലുകള്‍ (0, 0), (0, 1), (0.2), (0,3), (0, 4), (0. 5), (0, 6), (1, 4), (1, 3), (1, 2), (1,1), (2, 2), (2, 1), (3, 0), (2, 0), (1, 0) എന്നിവയാണ്‌. ഉപഭോഗബണ്ടിലുകളുടെ ഈ സമൂഹത്തെ ബജറ്റ്‌ സെറ്റ്‌ എന്നുപറയുന്നു.
ഇവിടെ ചില ബണ്ടിലുകളില്‍ ഉപഭോക്താവിന്റെ വരുമാനം പൂര്‍ണ്ണമായി ചെലവഴിച്ചിരിക്കുന്നു. (ഉദാ; (0, 6), (1, 4), (2, 2) (3, 0 ) എന്നിവയില്‍), എന്നാല്‍ ബാക്കി ബണ്ടിലുകളില്‍ ഉപഭോക്താവിന്റെ വരുമാനം പൂര്‍ണ്ണമായി ചെലവഴിച്ചിട്ടില്ല. (2, 4) എന്ന ബണ്ടില്‍ പരിഗണിക്കുക. ഇത്‌ വാങ്ങാന്‍ ഉപഭോക്താവിന്‌ കഴിയില്ല. ഇത്‌ വാങ്ങണമെങ്കില്‍ ഉപഭോക്താവിന്‌ 12 രൂപയില്‍ കൂടുതല്‍ വേണം. അതിനാല്‍ ഇത്‌ ബജറ്റ്‌ സെറ്റിന്റെ ഭാഗമല്ല.
ഉപഭോക്താവിന്റെ വരുമാനം 20 രൂപ. ഒന്നാമത്തെ സാധനത്തിന്റെ വില 5 രൂപ രണ്ടാമത്തെ സാധനത്തിന്റെ വില 4 രൂപ. ബജറ്റ്സെറ്റ്‌ രൂപികരിച്ചു നോക്കാം.
നമുക്ക് ലഭിക്കുന്ന ബജറ്റ് സെറ്റ് [(0, 0) (01, 0), (2, 0), 3, 0), (4, 0), (1,1),(1, 2), (1, 3), (2, 1), (2, 2), (3, 1), (0, 5) ] എന്നിവ ആയിരിക്കും.

ബജറ്റ്‌ പരിധി (Budget Constraint)
ഒരു ഉപഭോക്താവിന്റെ വരുമാനം “M”, സാധനങ്ങളുടെ വിലകള്‍ P₁, P₂ എന്നിവയുമാണ്‌ എന്ന്‌ കരുതുക. P₁ വിലയില്‍ അയാള്‍ x₁ അളവ്‌ സാധനം വാങ്ങുന്നു. അപ്പോള്‍ സാധനം 1 ല്‍ അയാളുടെ ചെലവ്‌ P₁x₁. ഇതുപോലെതന്നെ അയാള്‍ P₂ വിലയില്‍ x₂ അളവ്‌ സാധനം 2 വാങ്ങുന്നു. സാധനം 2 ല്‍ അയാളുടെ ചെലവ്‌ P₂x₂. അയാളുടെ മൊത്തം ചെലവ്‌ P₁x₁ + P₂x₂. മൊത്തം ചെലവ്‌ “M” ല്‍ കവിയാതെ അയാള്‍ക്ക്‌ ഏതുബണ്ടിലും വാങ്ങാം.

‘ഉപഭോക്താവിന് തന്റെ വരുമാനം ഭാഗികമായൊ പൂർണ്ണമായൊ ചെലവഴിക്കാം. ഉപഭോക്താവിന്റെ വരുമാനവും ചെലവും തമ്മിലുള്ള അസമതയെ ബജറ്റ് പരിധി അഥവാ അസമത്വം എന്നു പറയുന്നു.’

M ഉപഭോക്താവിന്റെ വരുമാനവും P₁, P₂ എന്നിവ സാധനങ്ങളുടെ വിലകളുമായാല്‍ P₁x₁ + P₂x₂ ≤ M എന്ന അസമതയെ (inequality) ബജറ്റ്‌ പരിധി (Budget Constraint)എന്നു പറയുന്നു.
M = 12 , P₁ = 4, P₂, = 2 ആയാല്‍ അവിടെ ബജറ്റ്‌ പരിധി എന്നത്‌ 4x₁ + 2x₂ ≤ 12 ആണ്‌. M ഉപഭോക്താവിന്റെ വരുമാനവും P₁, P₂, എന്നിവ സാധനങ്ങളുടെ വിലകളുമായാല്‍ P₁x₁ + P₂x₂ ≤ M എന്ന ബജറ്റ്‌ പരിധിക്കുള്ളിലുള്ള മുഴുവന്‍ ഉപഭോഗബണ്ടിലുകളേയും ബജറ്റ്‌ സെറ്റ്‌ എന്നുപറയാം.
ഉപഭോക്താവിന്റെ വരുമാനം 20 രൂപ. ഒന്നാമത്തെ സാധനത്തിന്റെ വില 5 രൂപ. രണ്ടാമത്തെ സാധനത്തിന്റെ വില 4 രൂപ ആയാല്‍ ബജറ്റ്‌ പരിധി (Budget Constraint)യുടെ അസമത രൂപികരിച്ചു നോക്കാം.
ബജറ്റ്‌ പരിധി (Budget Constraint)യുടെ അസമത 5x₁ + 4x₂ ≤ 20 എന്ന് ലഭിക്കും .

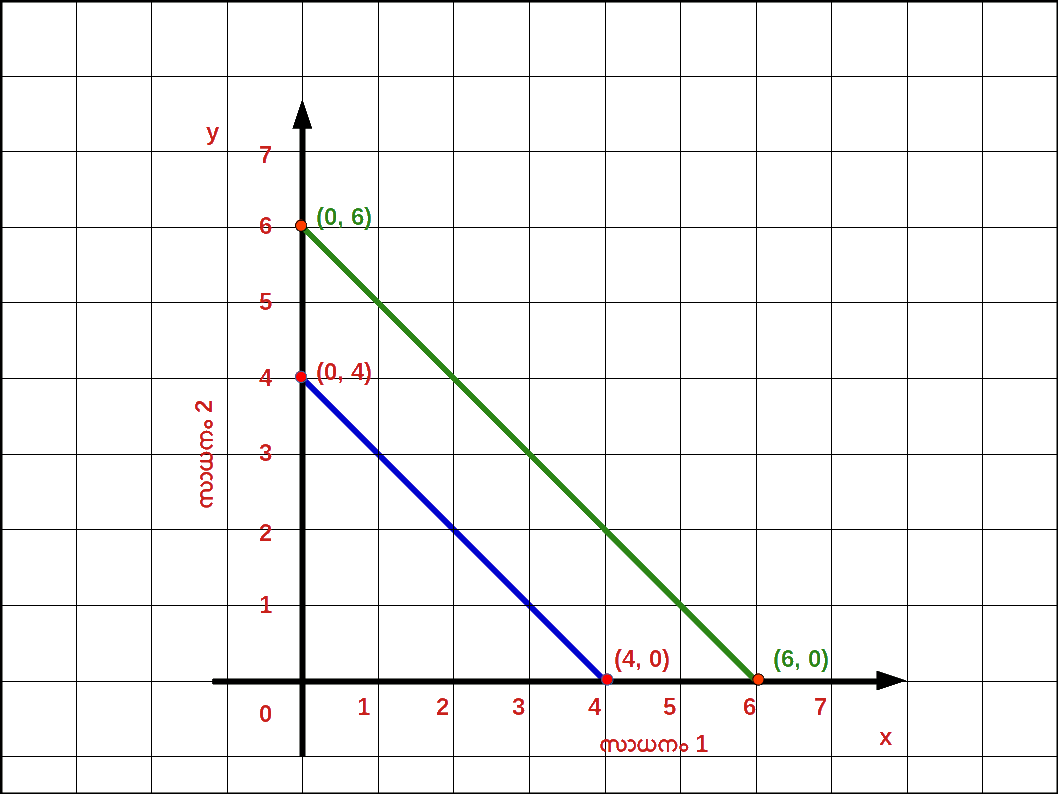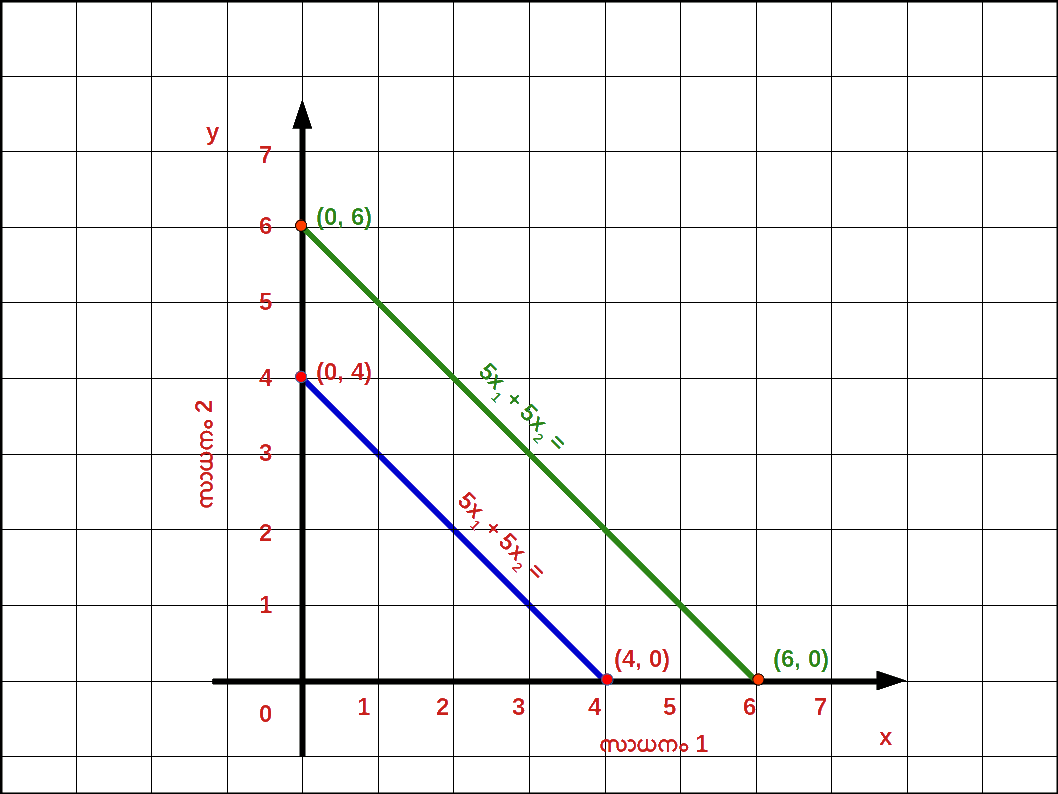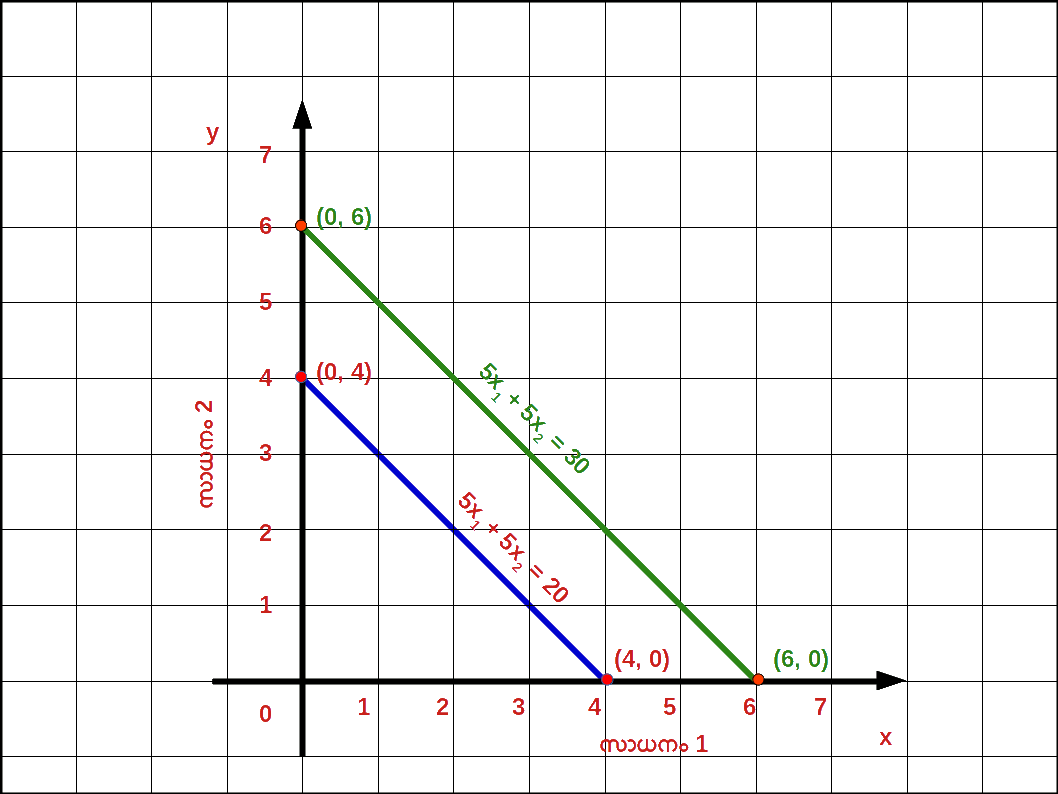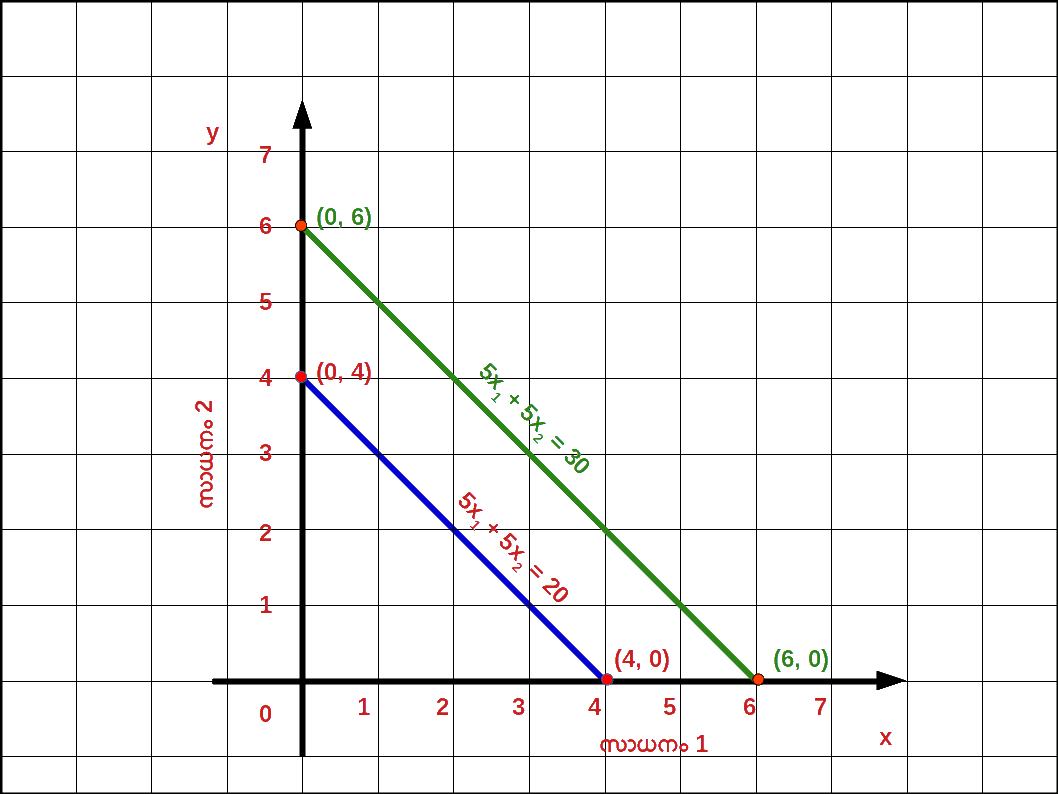
ബജറ്റ്‌ ലൈന്‍ (Budget Set)
ഒരു ഉപഭോക്താവിന്റെ വരുമാനം 12 രൂപ, സാധനം 1 ന്റെ വില 4 രൂപ, സാധനം 2 ന്റെ വില 2 രൂപ. ഇവിടെ ഉപഭോഗ ബണ്ടിലുകള്‍ (0, 0), (0, 1), (0.2), (0,3), (0, 4), (0. 5), (0, 6), (1, 4), (1, 3), (1, 2), (1,1), (2, 2), (2, 1), (3, 0), (2, 0), (1, 0) എന്നിവയാണ്‌. ഇത്‌ ഉപഭോക്താവിന്റെ ബജറ്റ്സെറ്റ്‌ ആണ്‌. സാധനം 1, x ആക്സിസിലും സാധനം 2, y ആക്‌സിസിലും അടയാളപ്പെടുത്തിക്കൊണ്ട്‌ ഈ ബണ്ടിലുകളെയെല്ലാം ഒരു ഗ്രാഫ്‌ പേപ്പറില്‍ രേഖപ്പെടുത്തുക. അപ്പോള്‍ ചുവടെ നലികിയിരിക്കുന്നതു പോലെയുള്ള ഒരു ഗ്രാഫ്‌ നമുക്ക്‌ ലഭിക്കും.

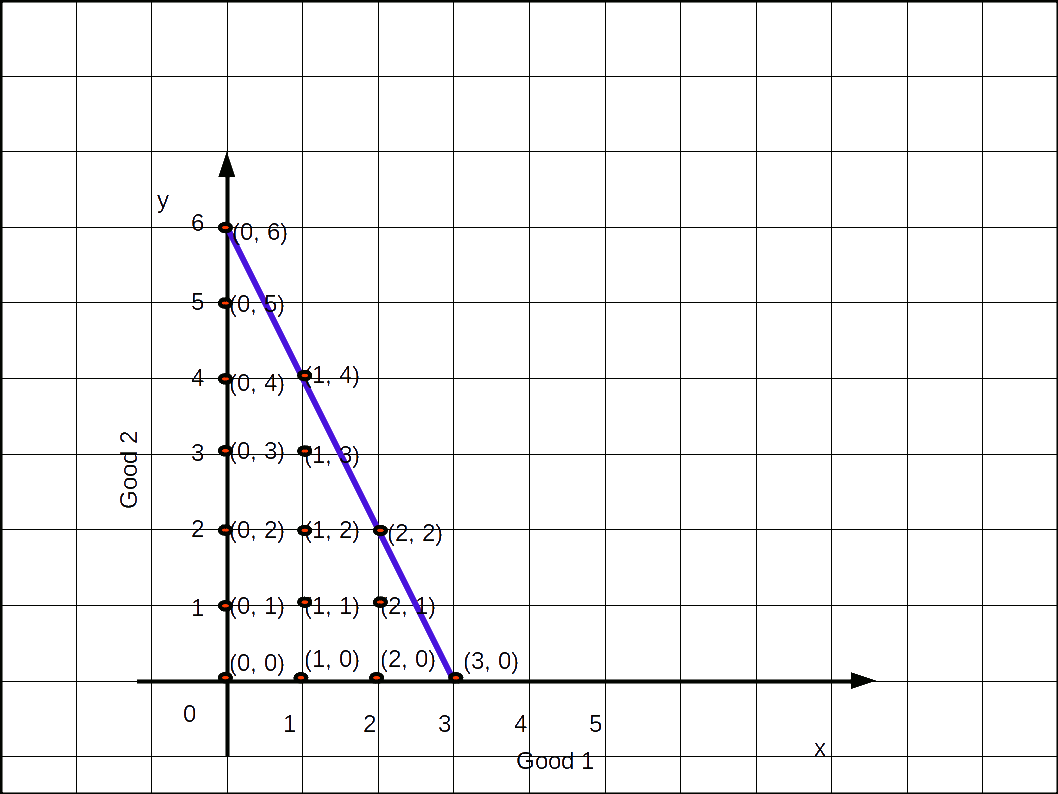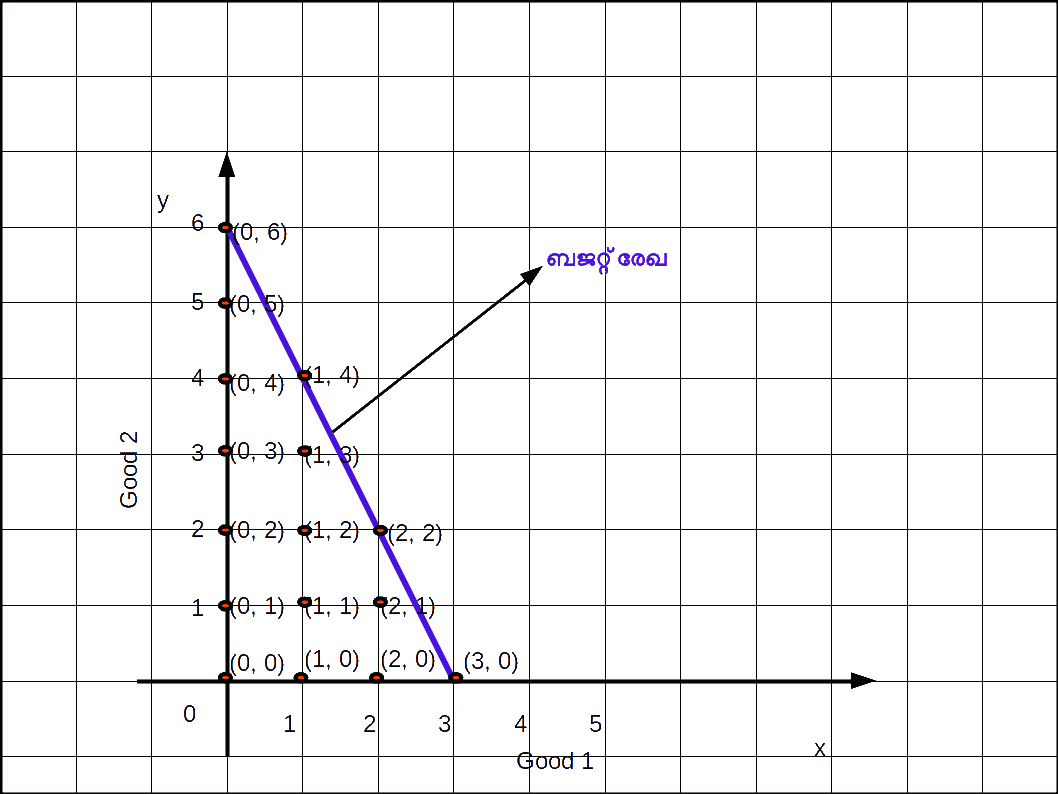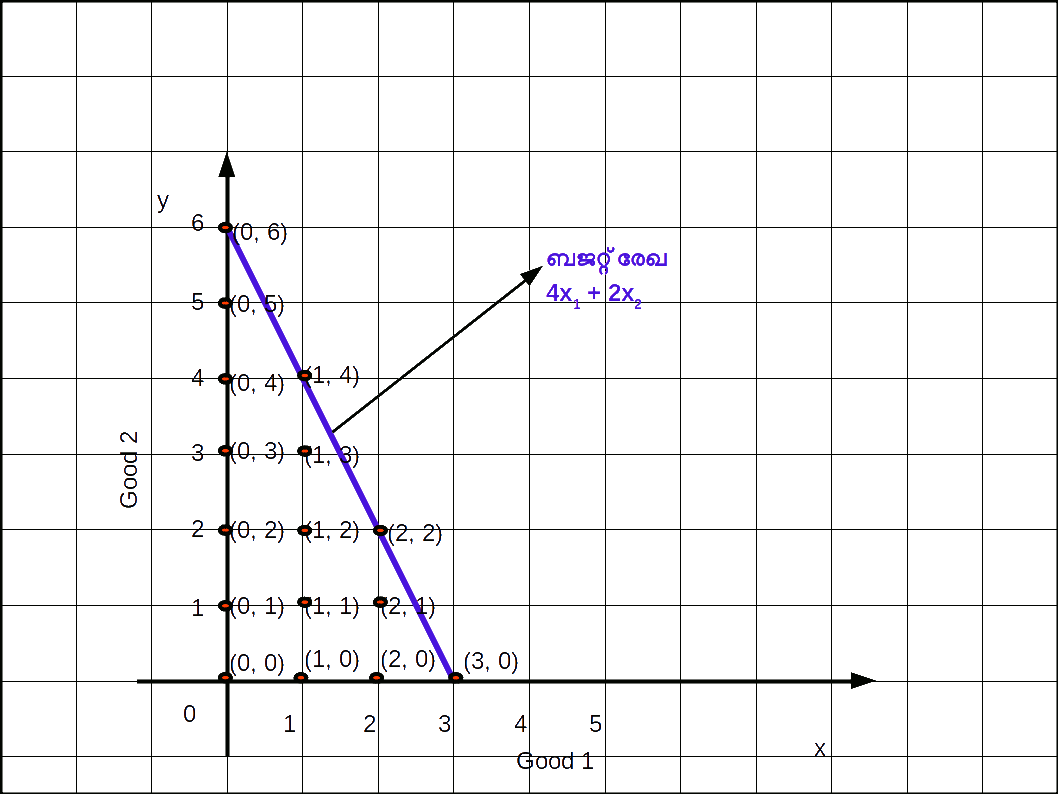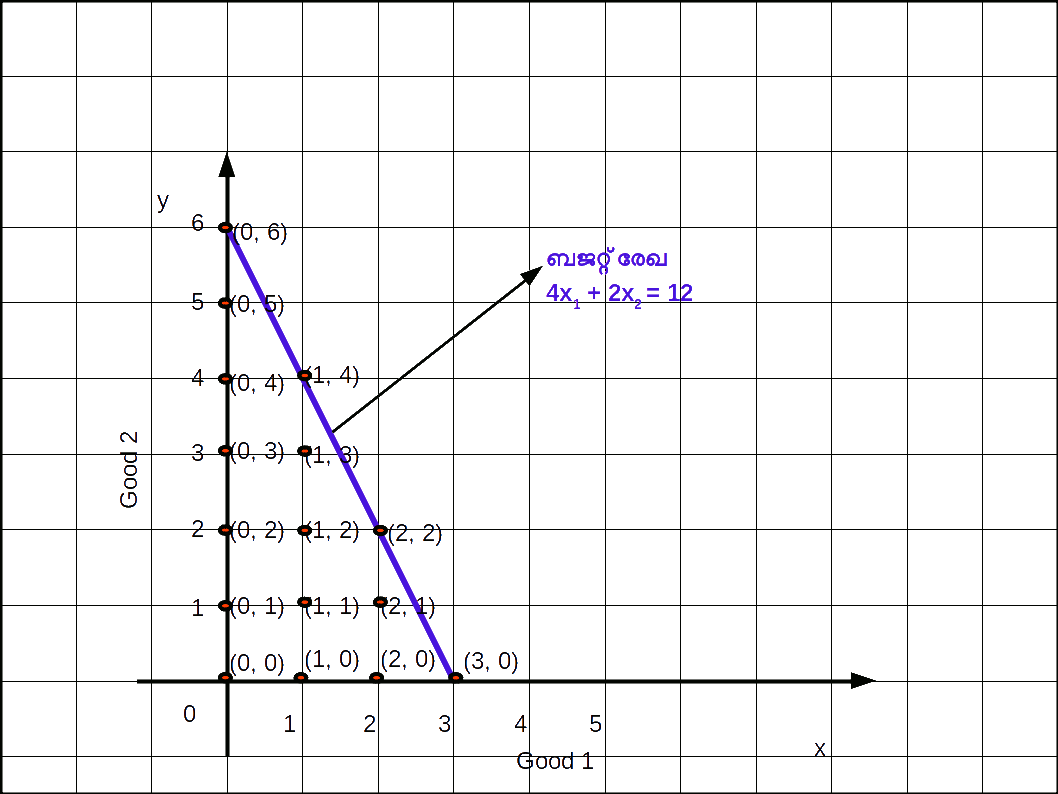
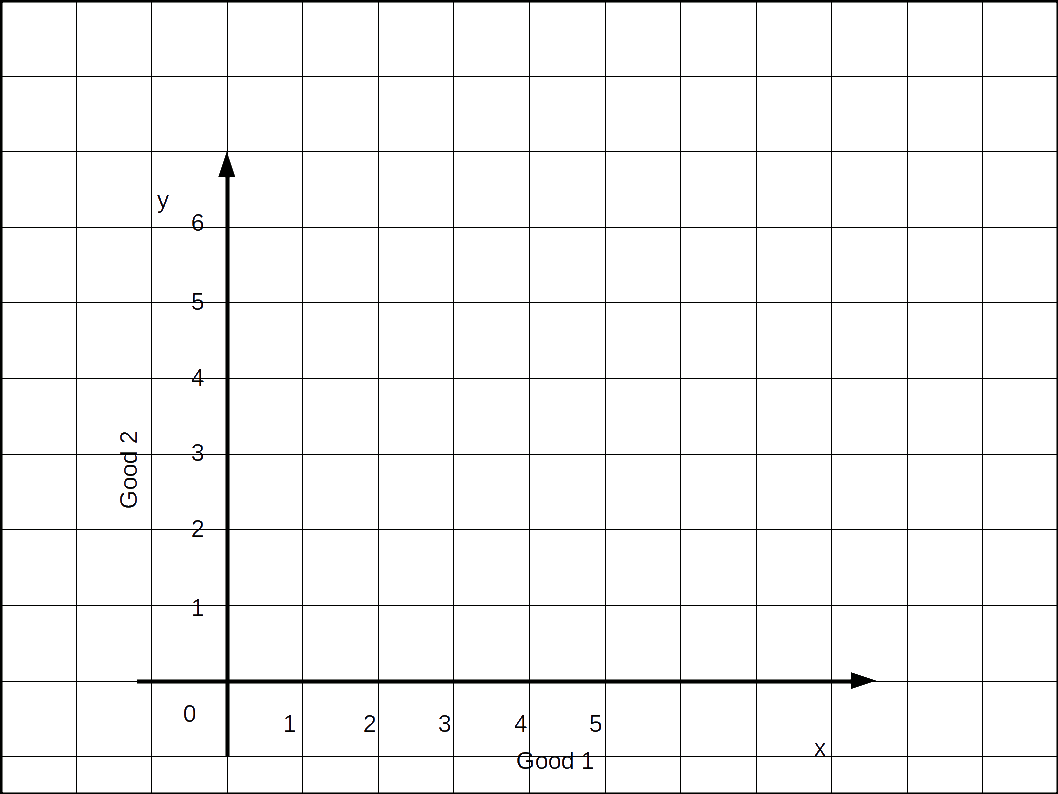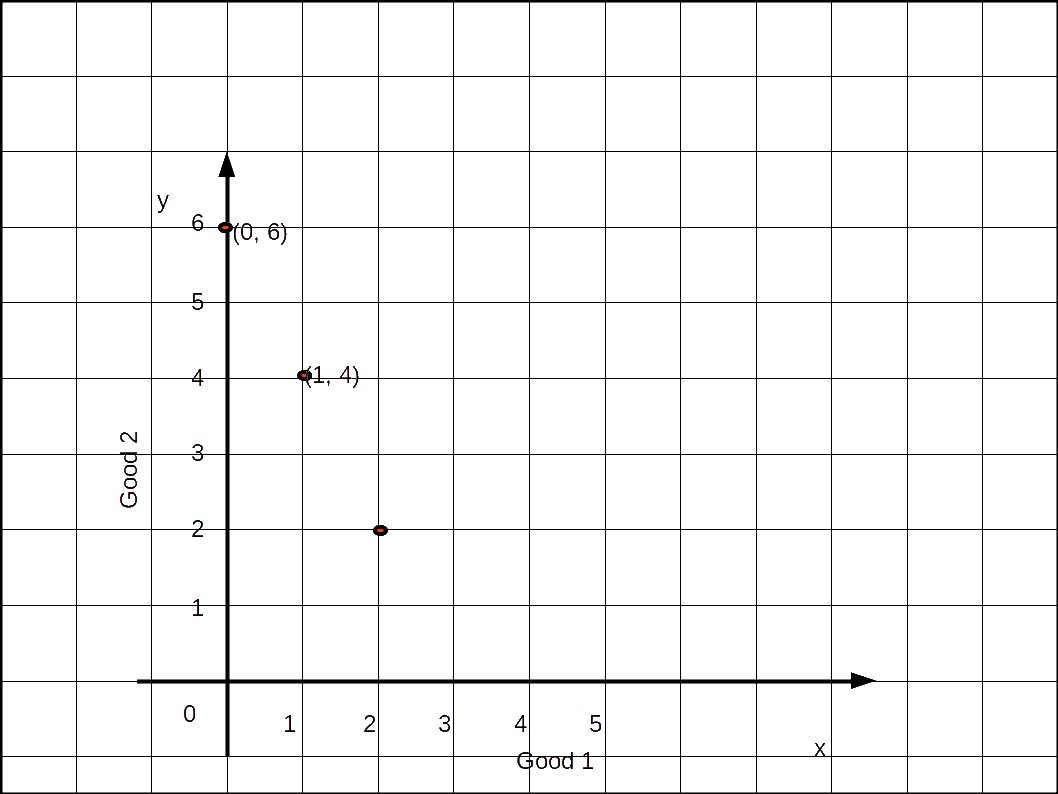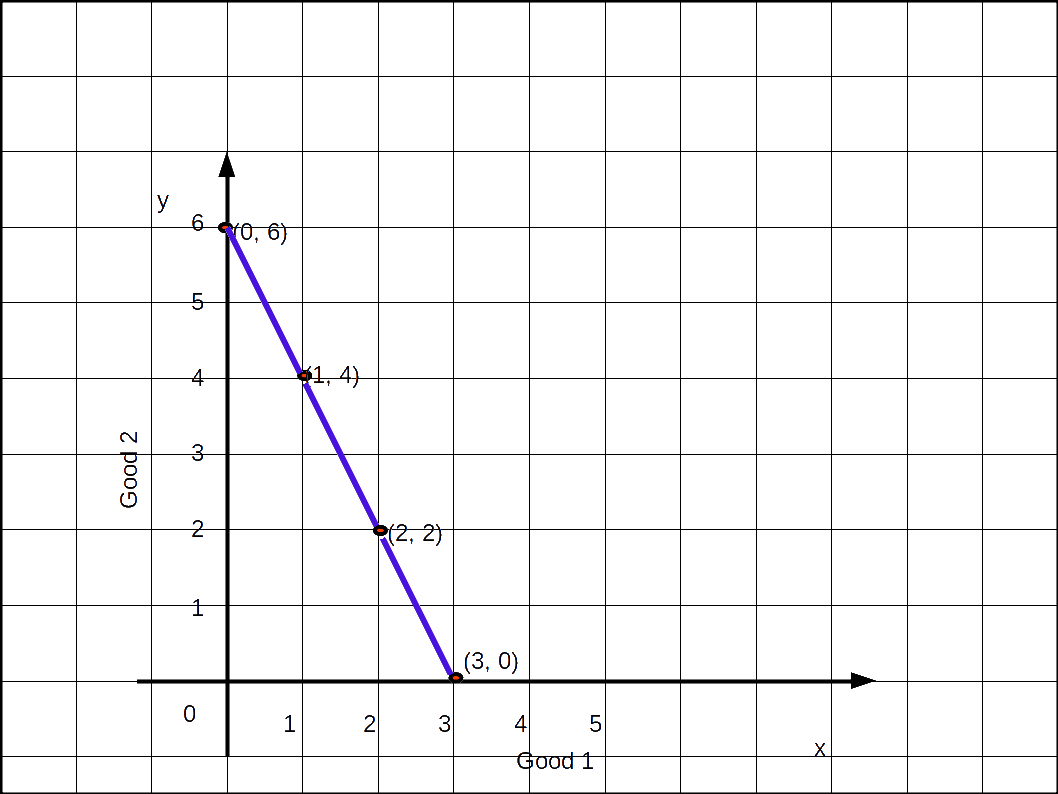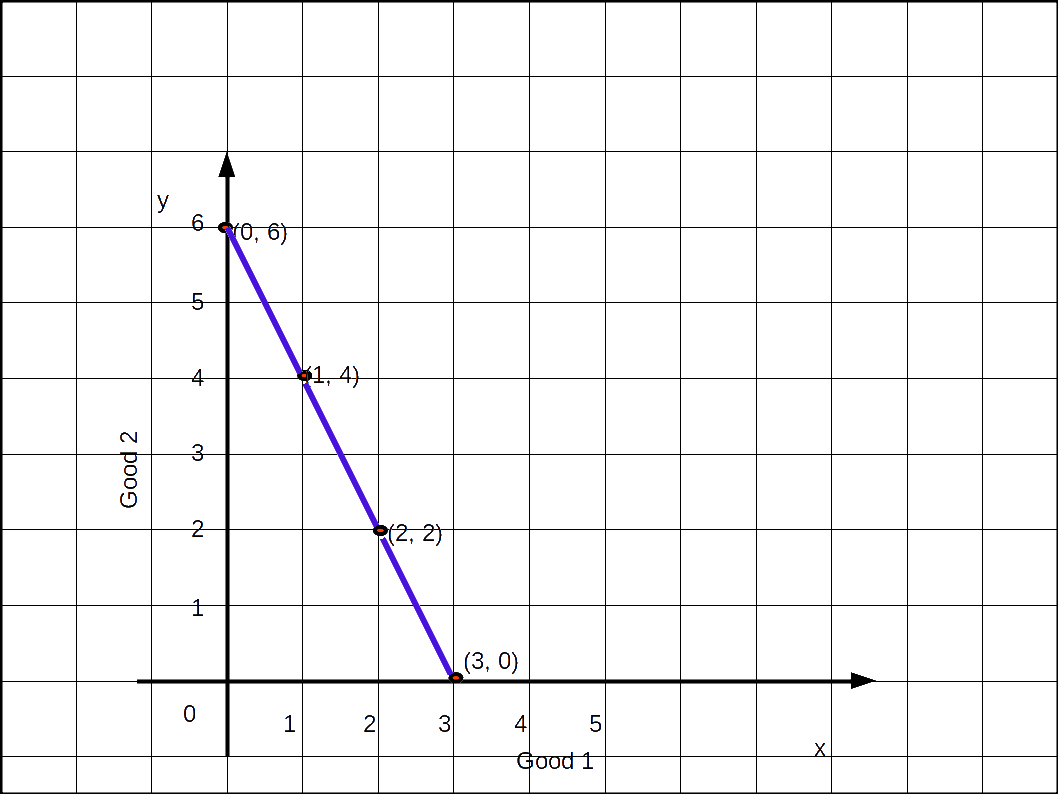
ഇവയില്‍ നിന്നും ഉപഭോക്താവ്‌ തന്റെ വരുമാനം പൂര്‍ണ്ണമായും ചെലവഴിച്ചിട്ടുള്ള ബണ്ടില്‍ തെരഞ്ഞെടുക്കുകയാണെങ്കിൽ (0, 6), (1, 4), (2, 2), (3, 0) എന്നിവയാണ് തെരഞ്ഞെടുക്കുക. ഈ ബിന്ദുക്കളെ തമ്മില്‍ യോജിപ്പിച്ചുകൊണ്ട്‌ ഒരു നേര്‍രേഖ വരയ്ക്കുക. ഇപ്രകാരം ലഭിക്കുന്ന രേഖയെ ബജറ്റ്‌ലൈന്‍ എന്നു പറയുന്നു.

‘രണ്ടു സാധനങ്ങള്‍ മാത്രമുള്ള സമ്പദ്‌വ്യവസ്ഥയില്‍ ഉപഭോക്താവിന്റെ വരുമാനം പൂര്‍ണ്ണമായി ചെലവഴിക്കപ്പെടുന്ന എല്ലാ ഉപഭോഗബണ്ടിലുകളെയും യോജിപ്പിച്ചുകൊണ്ട്‌ വരയ്ക്കുന്ന രേഖയെ ബജറ്റ്‌ രേഖ എന്നുപറയുന്നു.’

ബീജഗണിത രൂപത്തിൽ ബജറ്റ് രേഖയെ താഴെ നൽകിയ പോലെ എഴുതാം.

P₁ – ഒന്നാമത്തെ സാധനത്തിന്റെ വില

x₁ – ഒന്നാമത്തെ സാധനത്തിന്റെ അളവ്‌

P₂ – രണ്ടാമത്തെ സാധനത്തിന്റെ വില

x₂ – രണ്ടാമത്തെ സാധനത്തിന്റെ അളവ്‌

M – ഉപഭോക്താവിന്റെ വരുമാനം

ഉപഭോക്താവിന്റെ മൊത്തം ചെലവ്‌ = P₁x₁ + P₂x₂
ബജറ്റ്‌ ലൈനില്‍ ഉപഭോക്താവിന്റെ വരുമാനവും ചെലവും തുല്യമാണ്‌. അതിനാല്‍ ബജറ്റ്‌ ലൈനിന്റെ സമവാക്യം
P₁x₁ + P₂x₂ = M ______ (1)
അതായത്‌
$ {x_2 = {{{\frac{M}{P_2}} – {\frac{P_1}{P_2}}x_1 }} } $______ (2)
ബജറ്റ്‌ലൈന്‍ ഒരു നേര്‍രേഖ ആയിരിക്കും. ഇവിടെ വെര്‍ട്ടിക്കല്‍ ഇന്റെർസെപ്റ്റ് = $ {{{\frac{M}{P_2}}} } $ ചരിവ് = $ {{{\frac{-P_1}{P_2}}} } $ = വില അനുപാതം
ബജറ്റ്‌ ലൈനിന്റെ ചരിവിന്റെ ചിഹ്നം നെഗറ്റീവായത്‌ ബജറ്റ്‌ ലൈന്‍ താഴേക്ക്‌ ചരിഞ്ഞിരിക്കുന്നതിനെ സൂചിപ്പിക്കുന്നു. ബഡ്ജറ്റ് ലൈനിലുള്ള ഏതൊരുബിന്ദുവും സൂചിപ്പിക്കുന്നത് വ്യത്യസ്ത ബണ്ടിലുകളെയാണ്.
ഹൊറിസോണ്ടല്‍ ഇന്റെർസെപ്റ്റ് = $ {{{\frac{M}{P_1}}} } $
ബജറ്റ് ലൈന്‍ വരയ്ക്കുമ്പോൾ ‘x’ അക്ഷത്തില്‍ സാധനം 1 ന്റെ അളവും ‘y’ അക്ഷത്തില്‍ സാധനം 2 ന്റെ അളവും എടുക്കണം.

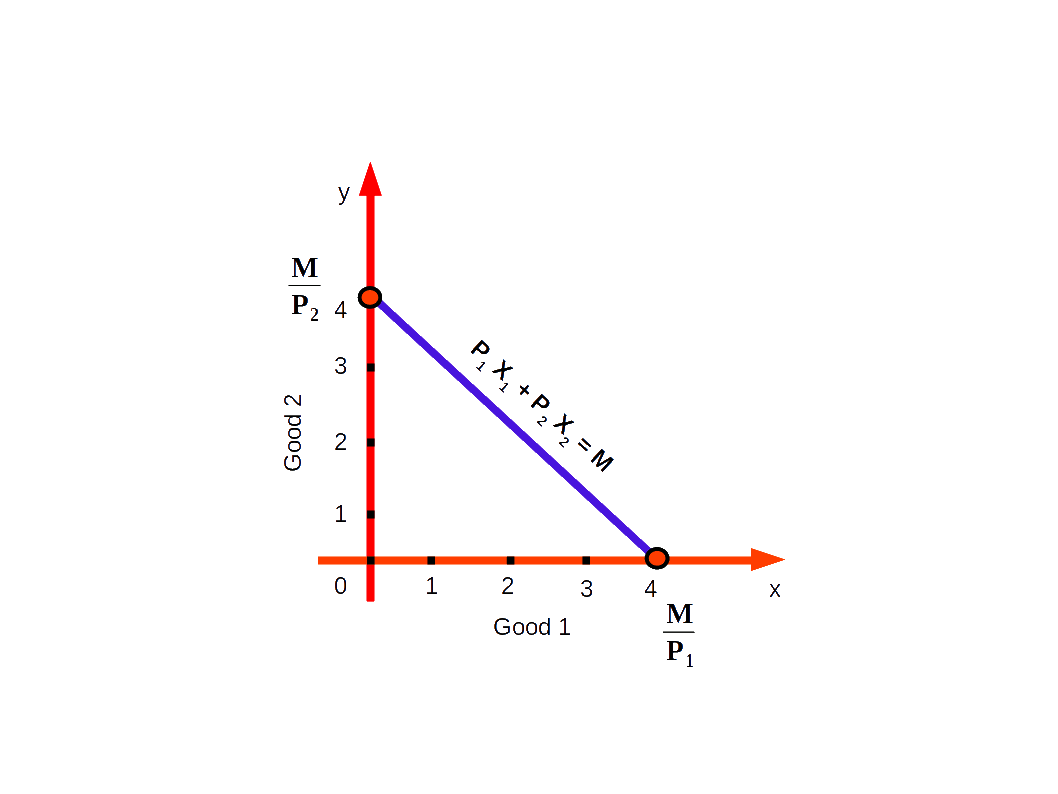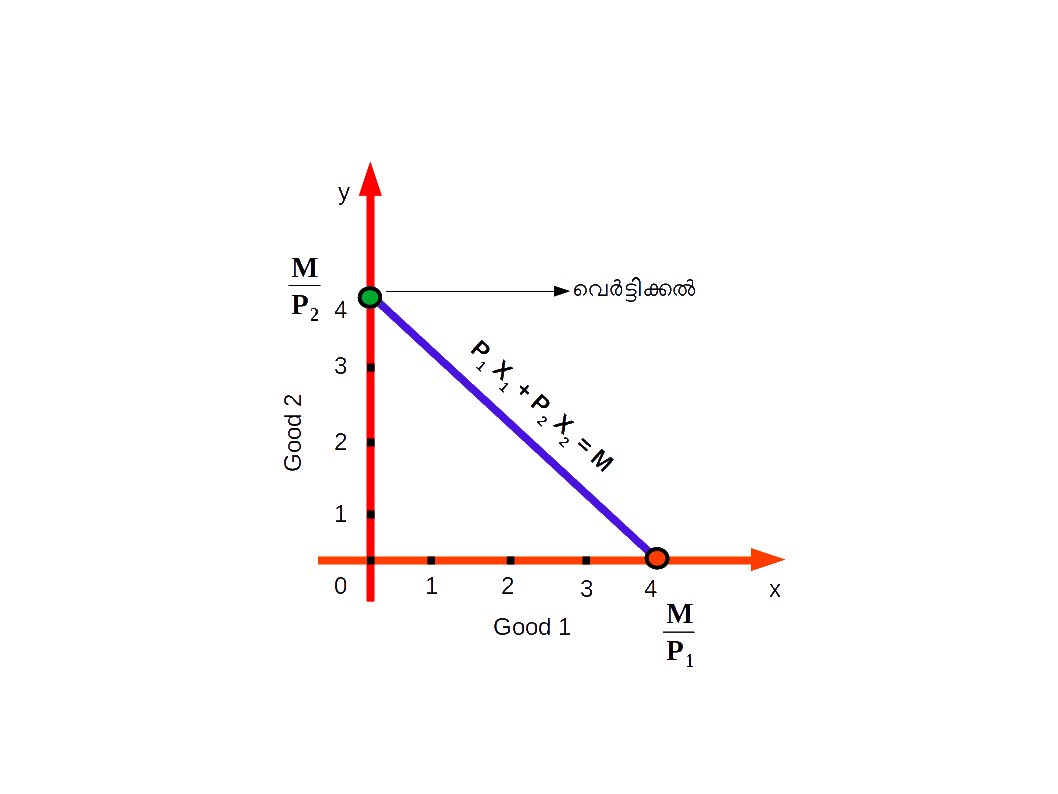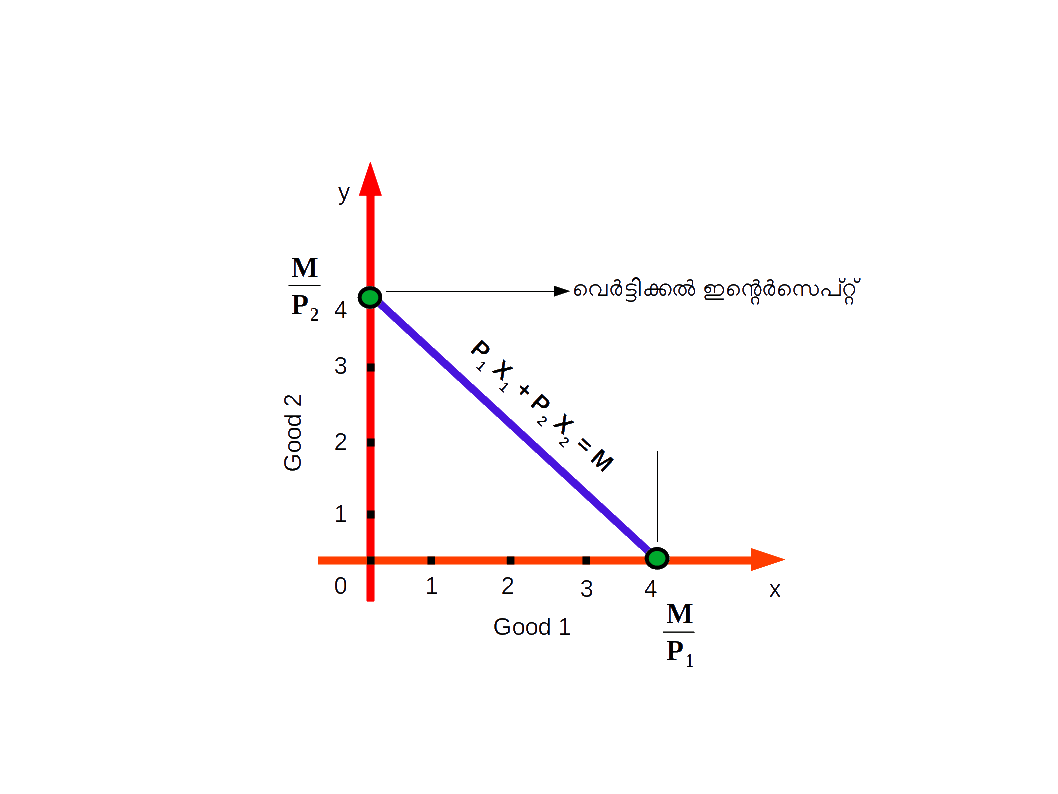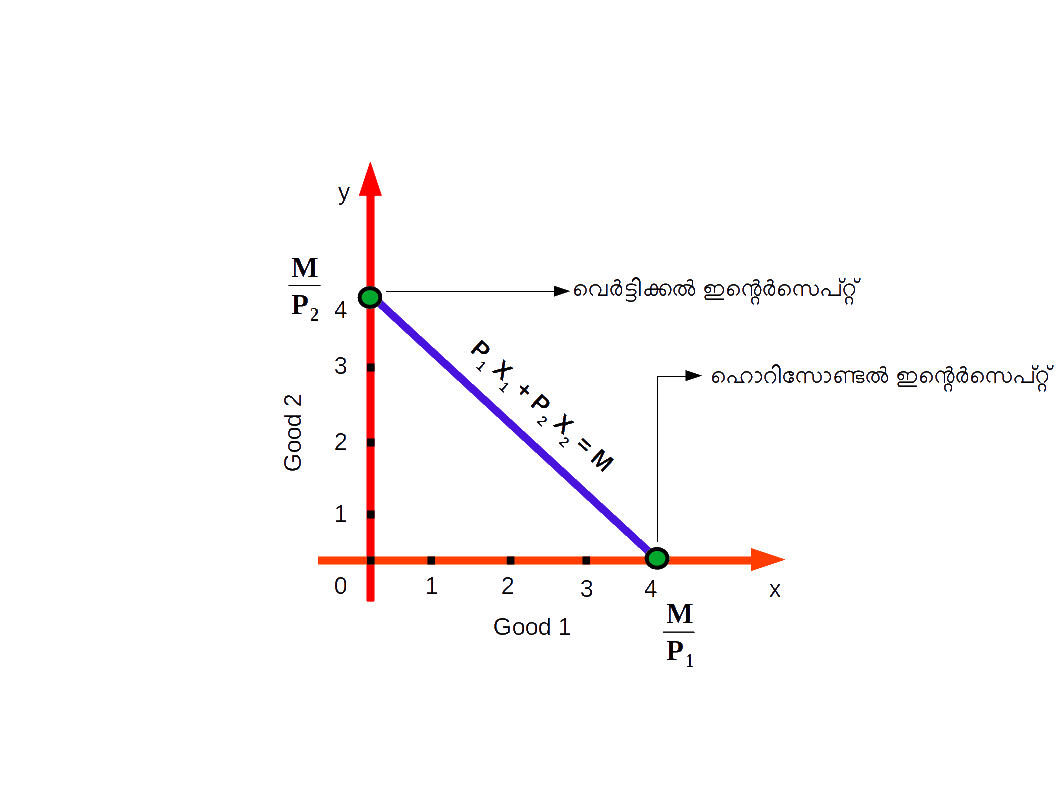
ബജറ്റ്‌ ലൈനിലെ എല്ലാ ബിന്ദുക്കളിലും വരുമാനം പൂര്‍ണ്ണമായി ചെലവഴിക്കപ്പെടുന്നു. ബജറ്റ്‌ ലൈനിലോ അതിനു താഴെയോ ഉള്ള മുഴുവന്‍ ഉപഭോഗബണ്ടിലുകളും ബജറ്റ്‌ സെറ്റില്‍ ഉള്‍പ്പെടുന്നു.

ബജറ്റ്‌ ലൈനിന്റെ സമവാക്യം
P₁x₁ + P₂x₂ = M ______ (1)
P₂x₂ = M – P₁x₁
$ {x_2 = {{{\frac{M – P_1x_1}{P_2}} }} }$
$ {x_2 = {{{\frac{M}{P_2}} – {\frac{P_1}{P_2}}x_1 }} }$______ (2)
സമവാക്യം (1) (2) എന്നിവ ഒരേ സമവാക്യങ്ങൾ തന്നെയാണ്.
ഒരു നേര്‍രേഖയുടെ പൊതുസമവാക്യം y = a + bx. ഇതുമായി സമവാക്യം (2) താരതമ്യപ്പെടുത്തുമ്പോൾ
a = വെര്‍ട്ടിക്കല്‍ ഇന്റെർസെപ്റ്റ് = $ {{{\frac{M}{P_2}}} } $
b = ചരിവ് = $ {{{\frac{-P_1}{P_2}}} } $

വെര്‍ട്ടിക്കല്‍ ഹൊറിസോണ്ടല്‍ ഇന്റർസെപ്റ്റുകളുടെ അര്‍ത്ഥവും, കണ്ടുപിടിക്കുന്ന വിധവും.

വെര്‍ട്ടിക്കല്‍ ഇന്റെർസെപ്റ്റ് .
P₁x₁ + P₂x₂ = M എന്ന സമവാക്യം എടുക്കുക.
ഉപഭോക്താവ്‌ രണ്ടാമത്തെ സാധനം (x₂) മാത്രം വാങ്ങൂന്നുവെന്ന്‌ കരുതുക, അതായത്‌ വരുമാനം മൂഴുവന്‍ രണ്ടാമത്തെ സാധനം (x₂) വാങ്ങുവാന്‍വേണ്ടി ചെലവഴിക്കുന്നു. അപ്പോള്‍ ഒന്നാമത്തെ സാധനം വാങ്ങുന്നതിന്റെ അളവ് (x₁) പൂജ്യം ആയിരിക്കും.
x₁ = 0 ആകുമ്പോള്‍
∴ P₁× 0 + P₂x₂ = M
P₂x₂ = M
$ {x_2 = {{{\frac{M}{P_2}} }} }$
അതിനാല്‍ ഈ ഉപഭോഗബണ്ടില്‍ (0, $ {{{{\frac{M}{P_2}} }} }$). ഇത്‌ ‘y’ അക്ഷത്തിലെ (വെര്‍ട്ടിക്കല്‍ അക്ഷം) ഒരു ബിന്ദുവാണ്‌. അതായത്‌ ബജറ്റ്‌ ലൈന്‍ ‘y’ അക്ഷത്തെ (വെര്‍ട്ടിക്കല്‍ അക്ഷത്തെ) ${{{{\frac{M}{P_2}} }} }$ എന്ന ബിന്ദുവിലാണ് ഖണ്ഡിക്കുക. അതിനാല്‍ ഇതിനെ വെര്‍ട്ടിക്കല്‍ ഇന്റെർസെപ്റ്റ് എന്നുപറയുന്നു.
വെർട്ടിക്കൽ ഇന്റർസെപ്റ്റിലെ ഉപഭോഗ ബണ്ടിൽ ശ്രദ്ധിക്കുക. (0, $ {{{{\frac{M}{P_2}} }} }$) ഇത് വരുമാനം മുഴുവൻ രണ്ടാമത്തെ സാധനം വാങ്ങുവാന്‍ ചെലവഴിക്കുമ്പോൾ (ഒന്നാമത്തെ സാധനത്തിന്റെ അളവ് 0 ആകുമ്പോൾ) വാങ്ങാന്‍ കഴിയുന്ന രണ്ടാമത്തെ സാധനത്തിന്റെ അളവിനെ സൂചിപ്പിക്കുന്നു.

ഹൊറിസോണ്ടല്‍ ഇന്റര്‍സെപ്റ്റ്‌.
P₁x₁ + P₂x₂ = M എന്ന സമവാക്യം എടുക്കുക. അയാളുടെ വരുമാനം മുഴുവന്‍ ഒന്നാമത്തെ സാധനം (x₁)വാങ്ങാന്‍ ചെലവഴിക്കുന്നു എന്ന്‌ കരുതുക. ഇവിടെ രണ്ടാമത്തെ സാധനം വാങ്ങുന്നതിന്റെ അളവ്‌ (x₂) പൂജ്യം.
x2 = 0 ആകുമ്പോള്‍
∴ P₁x₁ + P₂× 0 = M
P₁x₁ = M
$ {x_1 = {{{\frac{M}{P_1}} }} }$
ഉവിടെ ഉപഭോഗബണ്ടില്‍ ($ {{{{\frac{M}{P_1}} }} }$, 0) ആണ്‌. ഇത്‌ ‘x’ അക്ഷത്തിലെ ബിന്ദുവാണ്‌. അതായത്‌, ബജറ്റ്‌ ലൈന്‍ ‘x’ അക്ഷത്തില്‍ (ഹൊറിസോണ്ടല്‍ അക്ഷത്തില്‍) $ {{{{\frac{M}{P_1}} }} }$ എന്ന ബിന്ദുവിലായിരിക്കും ഖണ്ഡിക്കുക. ഹൊറിസോണ്ടല്‍ ഇന്റര്‍സെപ്റ്റിലെ ഉപഭോഗബണ്ടില്‍ ($ {{{{\frac{M}{P_1}} }} }$, 0) ഉപഭോക്താവിന്റെ വരുമാനം മുഴുവന്‍ ഒന്നാമത്തെ സാധനം വാങ്ങാന്‍ ചെലവഴിക്കുമ്പോള്‍ വാങ്ങാന്‍ കഴിയുന്ന ഒന്നാമത്തെ സാധനത്തിന്റെ അളവിനെ സൂചിപ്പിക്കുന്നു.

ബജറ്റ്‌ ലൈനിന്റെ ചരിവ്‌ കണ്ടെത്തുന്ന വിധം
ബജറ്റ്‌ലൈന്‍ P₁x₁ + P₂x₂ = M
$ {x_2 = {{{\frac{M}{P_2}} – {\frac{P_1}{P_2}}x_1 }} } $
ഇവിടെ ബജറ്റ്‌ ലൈന്‍ ഒരു നേര്‍രേഖയാണെന്ന്‌ നാം സങ്കലിപിച്ചിരിക്കൂന്നു. ഒരു നേര്‍രേഖയുടെ സമവാക്യത്തിന്റെ പൊതുവായ രൂപമെന്നത് y = a + bx ആണ്.
അതിന്റെ ചരിവ്‌ = bx
സമവാക്യവുമായി താരതേമ്യം ചെയ്യുമ്പോള്‍ ചരിവ് = $ {{{\frac{-P_1}{P_2}}} } $ = വില അനുപാതം
(x₁y₁), (x₂y₂) എന്നിവ ഒരു നേര്‍രേഖയിലെ രണ്ട്‌ ബിന്ദുക്കളാണെങ്കില്‍. ആ രേഖയുടെ ചരിവ്‌ = $ {{{\frac{y_2 – y_1}{x_2 – x_1}}} } $
ഇവിടെ (x₁y₁) എന്ന ബിന്ദു ($ {{{{\frac{M}{P_1}} }} }$, 0)
(x₂y₂) എന്ന ബിന്ദു (0, $ {{{{\frac{M}{P_2}} }} }$)
∴ ചരിവ്‌ = $ { {{{\frac{( {{{{\frac{M}{P_2}} }} }- 0)}{(0 – {{{{\frac{M}{P_1}} }} })}} }} }$ = $ { {{{\frac{ {{{{\frac{M}{P_2}} }} }}{ – {{{{\frac{M}{P_1}} }} }}} }} }$
$ {{{{\frac{M}{P_2}} }} }$ × $ {{{\frac{-P_1}{M}}} } $ = $ {{{\frac{-P_1}{P_2}}} } $
ബജറ്റ്‌ ലൈനിന്റെ ചരിവ്‌ = $ {{{\frac{-P_1}{P_2}}} } $
M = 12, P₁ = 4, P₂ = 2 ആയാല്‍

ബജറ്റ്‌ ലൈന്‍ രൂപീകരിക്കുക.

ബജറ്റ്‌ ലൈനിലെ ഉപഭോഗബണ്ടിലൂകള്‍ കണ്ടെത്തുക.

വെര്‍ട്ടിക്കല്‍ ഇന്റര്‍സെപ്റ്റ്‌, ഹൊറിസോണ്ടല്‍ ഇന്റര്‍സെപ്റ്റ്‌, ചരിവ്‌ (Slope) ഇവ കണ്ടെത്തുക.

ബജറ്റ്‌ ലൈന്‍ വരയ്ക്കുക.

1) 4x₁ + 2x₂ = 12
ബജറ്റ്‌ ലൈനിനെ താഴെപ്പറയുന്ന രൂപത്തില്‍ മാറ്റുവാന്‍ സാധിക്കും.
$ {x_2 = {{{\frac{M}{P_2}} – {\frac{P_1}{P_2}}x_1 }} }$
${\frac{M}{P_2}}$ = ${\frac{12}{6}}$ = 6
${\frac{P_1}{P_2}}$ = ${\frac{4}{2}}$ = 2
∴ x₂ = 6 – 2x₁
2) ഈ ബജറ്റ്‌ ലൈനിലെ ഉപഭോഗബണ്ടിലുകള്‍ കണ്ടെത്താന്‍ താഴെ നൽകിയ പോലെ പട്ടിക രൂപീകരിക്കാം.

Table 2.1

x₁ x₂ = 6 – 2x₁ ഉപഭോഗബണ്ടിലുകള്‍

0 x₂ = 6 – 2 × 0 = 6 (0, 6)

1 x₂ = 6 – 2 × 1 = 4 (1, 4)

2 x₂ = 6 – 2 × 2 = 2 (2, 2)

3 x₂ = 6 – 2 × 3 = 0 (3, 0)

3) ഇവിടുത്തെ വെര്‍ട്ടിക്കല്‍ ഇന്റര്‍സെപ്റ്റ്‌
= ${\frac{M}{P_2}}$ = ${\frac{12}{2}}$ = 6
ഹൊറിസോണ്ടല്‍ ഇന്റര്‍സെപ്റ്റ്‌
= ${\frac{M}{P_1}}$ = ${\frac{12}{4}}$ = 3
ചരിവ്‌ = $ {{{\frac{-P_1}{P_2}}} } $ =$ {{{\frac{-4}{2}}} } $ = -2
4)

ബജ്‌ ലൈന്‍ വരയ്ക്കാന്‍ ഉപഭോഗബണ്ടിലുകള്‍ മുഴുവന്‍ ഗ്രാഫില്‍ അടയോളപ്പെടുത്തണമെന്നില്ല, അതിനായി വെര്‍ട്ടിക്കല്‍ ഇന്റർസെപ്റ്റും ഹൊറിസ്പോണ്ടല്‍ ഇന്റർസെപ്റ്റും കണ്ടെത്തി അവമാത്രം ഗ്രാഫില്‍ അടയാളപ്പെടുത്തി യോജിപ്പിച്ചാലും ബജറ്റ്‌ ലൈന്‍ കിട്ടും.
ഇവിടെ വെര്‍ട്ടിക്കല്‍ ഇന്റര്‍സെപ്റ്റ്‌ = ${\frac{M}{P_2}}$ = ${\frac{12}{2}}$ = 6
ഉപഭോഗബണ്ടില്‍ (0, 6)
ഹൊറിസോണ്ടല്‍ ഇന്റര്‍സെപ്റ്റ്‌ = ${\frac{M}{P_1}}$ = ${\frac{12}{4}}$ = 3
ഉപഭോഗബണ്ടില്‍ (3, 0)
(0, 6), (3, 0) എന്നീ ബണ്ടിലുകള്‍ ഗ്രാഫില്‍ അടയാളപ്പെടുത്തി നേര്‍രേഖ വരയ്ക്കുക. ഇത്‌ ബജറ്റ്‌ ലൈനായിരിക്കും.

വില അനുപാതവും ബജറ്റ്‌ ലൈനിന്റെ ചരിവും.(Price Ratio and Slope of the Budget Line)
ബജറ്റ്‌ ലൈനിലെ ഓരോ ബിന്ദുവും ഉപഭോക്താവിന്റെ വരുമാനം മുഴുവന്‍ ചെലവാക്കുന്ന ഉപഭോഗബങണ്ടിലുകളെ സൂചിപ്പിക്കുന്നു. ബജറ്റ്‌ ലൈനിലായിരിക്കുന്ന ഒരു ഉപഭോക്താവിന്‌ ഒന്നാമത്തെ സാധനത്തിന്റെ അളവ്‌ ഒരു യുണിറ്റ്‌ കൂടി കൂടുതലായി വേണമെങ്കില്‍ അയാള്‍ രണ്ടാമത്തെ സാധനം വാങ്ങുന്നതിന്റെ അളവ്‌ കുറയ്ക്കേണ്ടിവരും. രണ്ടാമത്തെ സാധനത്തിന്റെ അളവ്‌ എത്രമാത്രം കുറയ്ക്കേണ്ടിവരുമെന്നത്‌ രണ്ടു സാധനങ്ങളുടെയും വിലയെ ആശ്രയിച്ചിരിക്കുന്നു. ഒന്നാമത്തെ സാധനത്തിന്റെ വില P₁ ആയതിനാല്‍ ഒന്നാമത്തെ സാധനം ഒരു യൂണിറ്റുകൂടി വേണമെങ്കില്‍ രണ്ടാമത്തെ സാധനത്തിയേലുള്ള ചെലവ്‌ P₁ അളവ്‌ കുറയ്‌ക്കേണ്ടിവരും. P₁ വിലകൊണ്ട്‌ ഉപഭോക്താവിന്‌ സാധനം 2 ന്റെ ${\frac{P_1}{P_2}}$ യൂണിറ്റ്‌ വാങ്ങാന്‍ കഴിയും. അതായത്‌ ഉപഭോക്താവിന്‌ ഒന്നാമത്തെ സാധനത്തിന്റെ ഒരു യൂണിറ്റുകൂടി വേണമെങ്കിൽ അയാള്‍ രണ്ടാമത്തെ സാധനത്തിന്റെ ${\frac{P_1}{P_2}}$ അളവ്‌ ത്യജിക്കണം.
${\frac{P_1}{P_2}}$ വില അനുപാതം എന്നറിയപ്പെടുന്നു. ഇതുതന്നെയാണ്‌ ബജറ്റ്‌ ലൈനിന്റെ ചരിവും.
ഒരു ബജറ്റ്‌ ലൈനിന്റെ ചരിവ്‌ (Slope) എന്നത്‌ ഒന്നാമത്തെ സാധനം ഒരു യൂണിറ്റുകൂടി വേണമെങ്കില്‍ രണ്ടാമത്തെ സാധനം എത്ര അളവ്‌ ത്യജിക്കണം എന്നതിനെ സൂചിപ്പിക്കുന്നു. ഇതുതന്നെയാണ്‌ വില അനുപാതവും സൂചിപ്പിക്കുക.

4x₁ + 2x₂ = 12 എന്ന ബജറ്റ്‌ ലൈന്‍ പരിഗണിക്കുക.
ഇവിടെ, ഒരു യൂണിറ്റ്‌ x₁ നേടുന്നതിന്‌, [(0, 6) എന്ന്‌ ബണ്ടിലില്‍ നിന്ന്‌ (1, 4) എന്ന ബണ്ടിലിലേക്കു പോകണമെന്നുണ്ടെങ്കില്‍] രണ്ടു യൂണിറ്റ്‌ സാധനം x₁ വേണ്ടെന്നു വയ്ക്കേണ്ടതായി വരും.

അതായത്‌ വില അനുപാതവും ബജറ്റ്‌ ലൈനിന്റെ ചരിവും ഒന്നുതന്നെയാണ്‌.
M = 12, P₁ = 4, P₂ ആയാല്‍ ബജറ്റ്‌ ലൈന്‍ 4x₁ + 2x₂ = 12 അഥവാ x₂ = 6 – 2x₁ ആണ്‌. ഇവിടെ ബജറ്റ്‌ ലൈനിന്റെ ചരിവി 2 ആണ്‌. ഇവിടെ ഒന്നാമത്തെ സാധനത്തിന്റെ വില 4 രൂപയാണ്‌. രണ്ടാമത്തെ സാധനത്തിന്റേത്‌ 2 രൂപയും.
ഉപഭോക്താവ്‌ എന്ന ബണ്ടില്‍ വാങ്ങുന്നുവെന്നിരിക്കട്ടെ. അപ്പോള്‍ സാധനം 1 നുള്ള ചെലവ്‌ = P₁x₁ = 4 × 0 = 0
സാധനം 2 നുള്ള ചെലവ്‌ = P₂x₂ = 6 × 2 = 12
ഇനി സാധനം 1 ഒരു യൂണിറ്റുകൂടി വാങ്ങുന്നുവെന്നിരിക്കട്ടെ. അതായത്‌,
സാധനം 1 നുള്ള പുതിയ ചെലവ്‌ = 1 × 4 = 4
അപ്പോള്‍ സാധനം 2 നുള്ള ചെലവ്‌ P₁, അളവ് (4 രൂപ) കുറയിക്കേണ്ടിവരും. ഇത്‌ 2 യൂണിറ്റ്‌ സാധനം 2ന്‌ തുല്യമാണ്‌. അതിനാല്‍ സാധനം 2ന്റെ അളവ് 2 യൂണിറ്റ്‌ കുറയിക്കേണ്ടിവരും. അതായത്‌ ഇവിടെ സാധനം 1 ഓരോ യൂണിറ്റ്‌ കൂടുതലായി വാങ്ങുമ്പോഴും സാധനം 2-ന്റെ 2 യൂണിറ്റു വീതം കുറയ്ക്കേണ്ടിവരും.
ഈ ഉദാഹരണത്തിലെ ബജറ്റ്‌ ലൈനിലെ ഉപഭോഗബനണ്ടിലുകള്‍ ശ്രദ്ധിക്കുക. (0, 6) (1, 4) (2, 2) (3, 0) എന്നിവയാണവ.
ഇവിടെ (0, 6) എന്ന ബണ്ടിലില്‍ നിന്നും (1, 4) ലേക്ക്‌ പോകുമ്പോള്‍ 1 യൂണിറ്റ്‌ സാധനം 1 നേടാനായി സാധനം 2ന്റെ രണ്ട്‌ യൂണിറ്റ്‌ കുറയ്ക്കേണ്ടിവരും. ഇവിടെ “2” എന്നത്‌ ബജറ്റ്‌ ലൈനിന്റെ ചരിവാണ്‌, അതുതന്നെയാണ്‌ വില അനുപാതവും $\biggl({\frac{P_1}{P_2}}\, = \,{\frac{4}{2}} \,=\, 2 \biggr)$

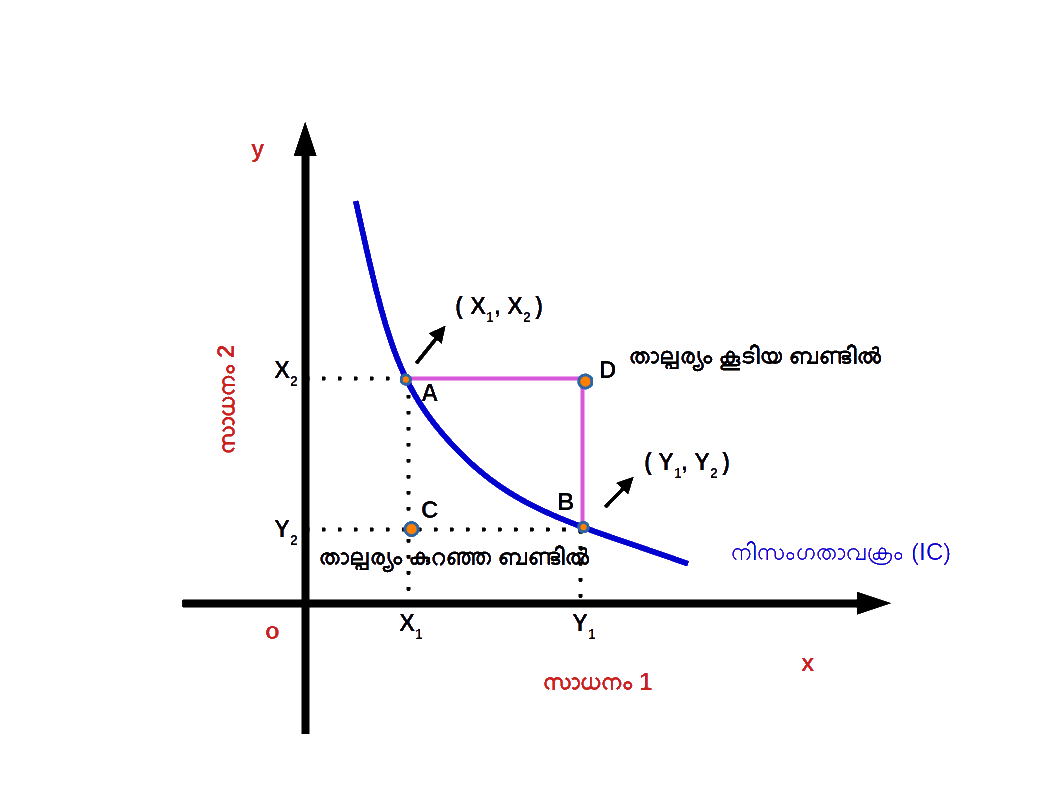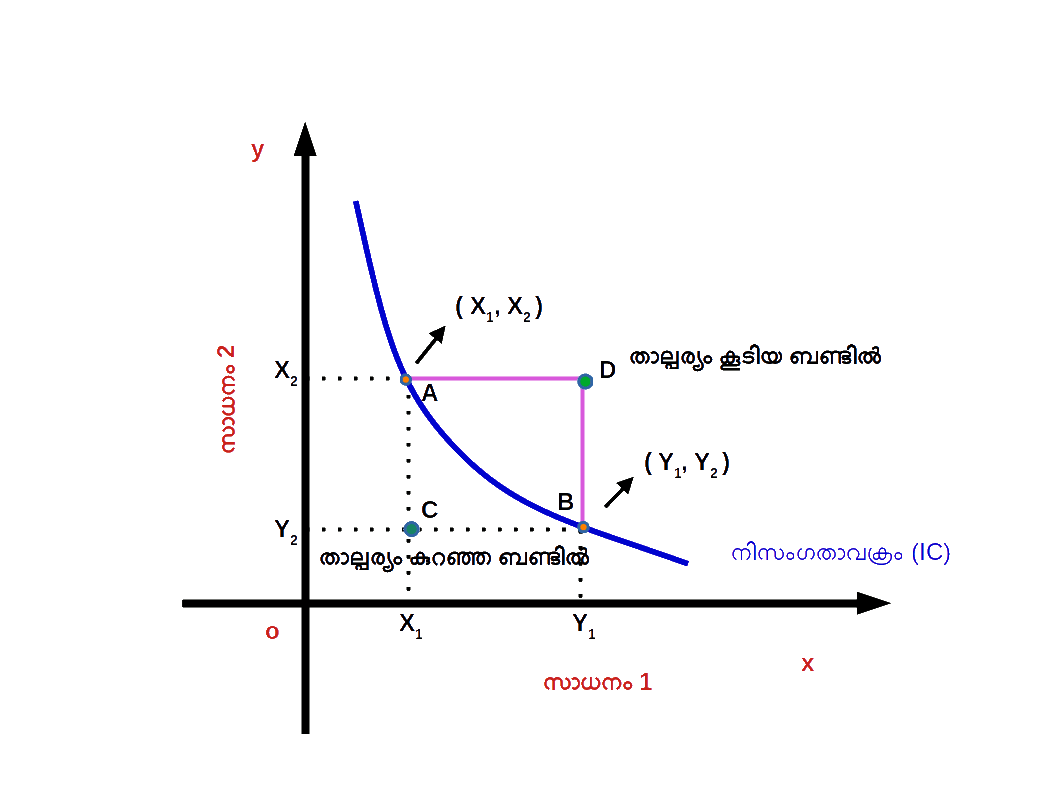
ബജറ്റ് ലൈനിലും മുകളിലും താഴെയുമുള്ള ബിന്ദുക്കൾ ( Points on , above and below the Budget Line )
ബജറ്റ് ലൈനിന് താഴെയുള്ള ഏതൊരു ബണ്ടി ലിലും ഉപഭോക്താവ് തന്റെ വരുമാനം മുഴുവനായും ചെലവഴിക്കുന്നില്ല. കുറച്ച് പണം ഉപഭോക്താവിന്റെ കൈയിൽ ബാക്കിയുണ്ടാകുന്നു. ഈ മിച്ചമുള്ള പണം ഉപയോഗിച്ച് അയാൾക്ക് സാധനം 1 ന്റെയോ സാധനം 2 ന്റെയോ അല്ലെങ്കിൽ രണ്ട് സാധനങ്ങളുടെയും കൂടുതൽ അളവ് വാങ്ങാൻ കഴിയും. ഡയഗ്രം 2.6 ൽ A , B എന്നീ ബിന്ദുക്കൾ ബജറ്റ് ലൈനിലാണ്. C എന്ന ബിന്ദു ബജറ്റ് ലൈനിന് താഴെയാണ് . A എന്ന ബിന്ദുവിൽ അയാൾ സാധനം 1 ന്റെ 1 യൂണിറ്റും സാധനം 2 ന്റെ 3 യൂണിറ്റും ( 1 , 3 ) വാങ്ങുന്നു. B എന്ന ബിന്ദുവിൽ സാധനം 1 ന്റെ 3 യൂണിറ്റും സാധനം 2 ന്റെ 1 യൂണിറ്റും ( 3 , 1 ) വാങ്ങുന്നു. A , B എന്നീ ബണ്ടിലുകൾ കാര്യക്ഷമമായ ബണ്ടിലുകൾ എന്നറിയപ്പെടുന്നു. എന്നാൽ C എന്ന ബിന്ദുവിൽ 1 യൂണിറ്റ് സാധനം 1 ഉം 1 യൂണിറ്റ് സാധനം 2 ഉം ( 1 , 1 ) വാങ്ങുന്നു. അപ്പോൾ C യിൽ സാധനങ്ങൾക്കുള്ള ചെലവ് അയാളുടെ വരുമാനത്തെക്കാൾ കുറഞ്ഞിരിക്കും. ഈ ബണ്ടിൽ മേന്മ കുറഞ്ഞ ബണ്ടിൽ എന്നറിയപ്പെടുന്നു. എന്നാൽ D എന്ന ബിന്ദു ബജറ്റ് ലൈനിന് വെളിയി ലാണ്. ഈ ബണ്ടിൽ വാങ്ങാൻ ഉപഭോക്താവിന്റെ വരുമാനം തികയുകയില്ല. ഈ ബണ്ടിലിന് ബജറ്റ് ലൈനിലുള്ള ബണ്ടിലിനെക്കാൾ മേന്മ കൂടുതലായിരിക്കും. ഇതിനെ മേന്മ കൂടിയ ബണ്ടിൽ എന്നറിയപ്പെടുന്നു.

Diagram 2.6

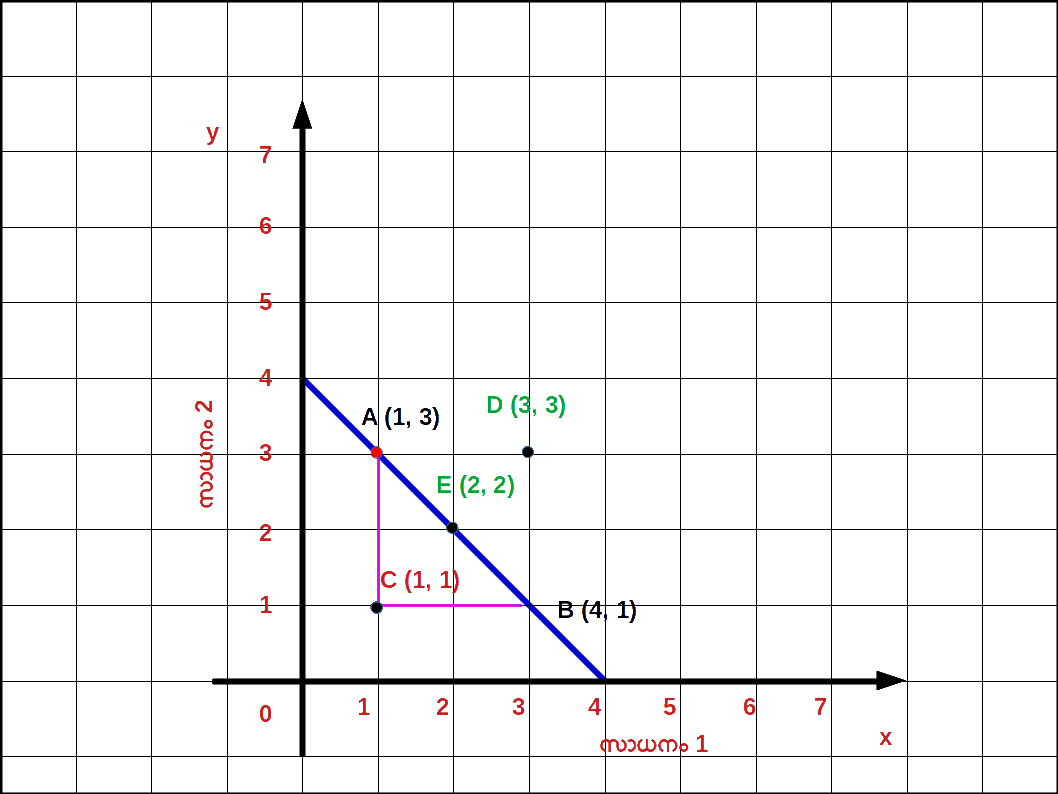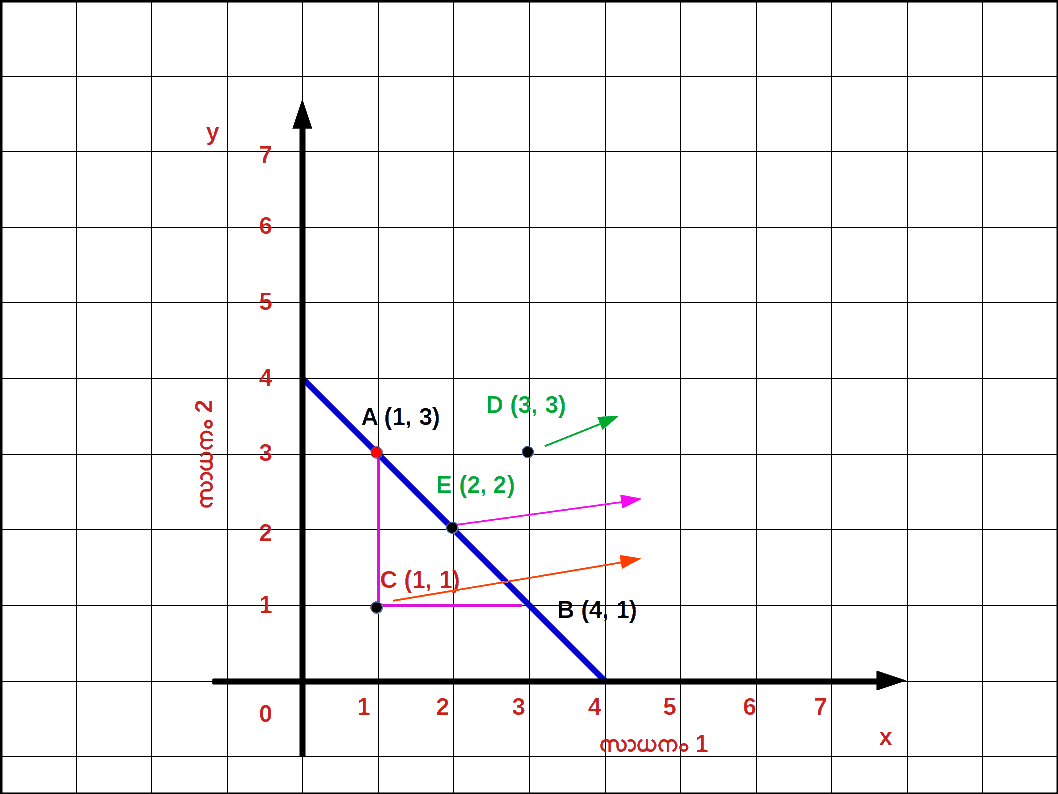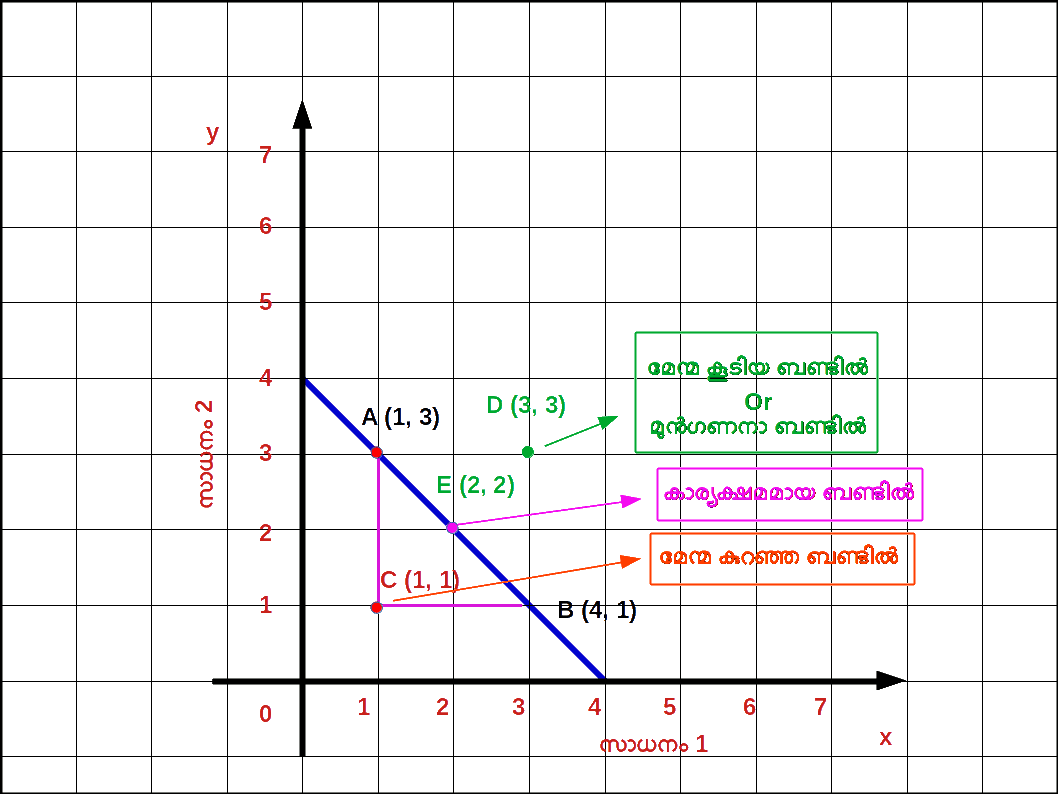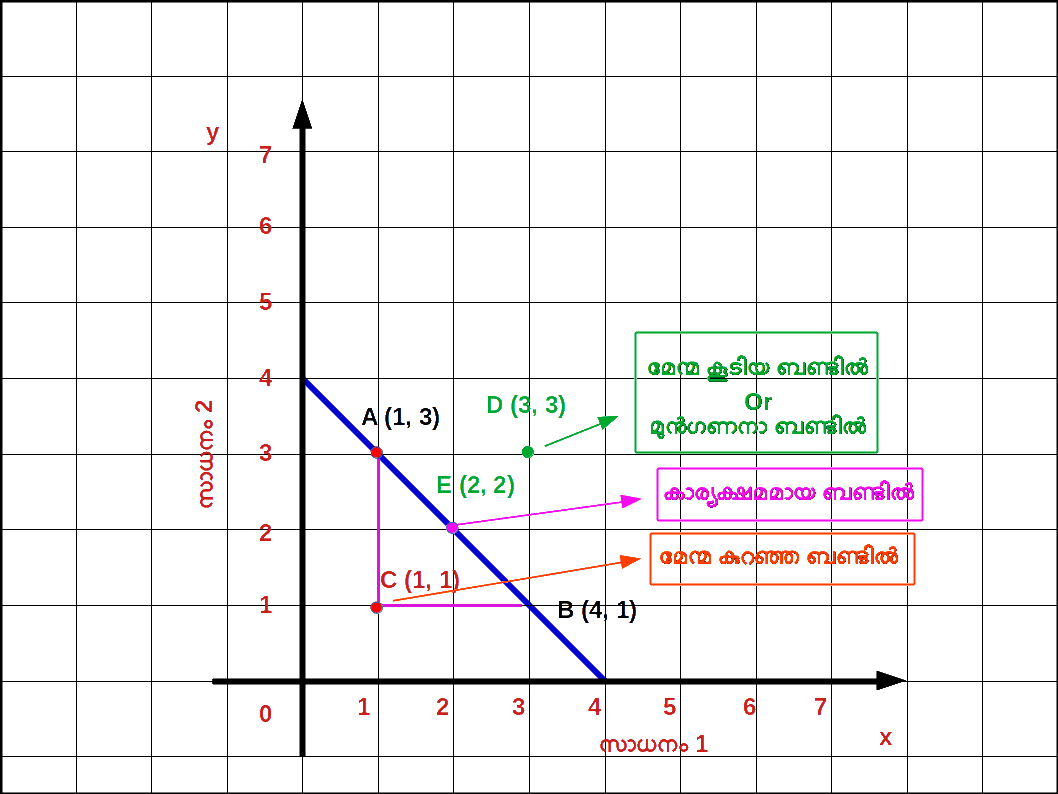
1 ) ബജറ്റ് ലൈനിലുള്ള ഏതൊരു ബിന്ദുവും സൂചിപ്പിക്കുന്നത് ഒരു ഉപഭോക്താവിന് അദ്ദേഹത്തിന്റെ വരുമാനം പൂർണമായും ഉപയോഗിച്ചുകൊണ്ട് വാങ്ങാൻ സാധിക്കുന്ന സാധനം 1 ന്റെയും സാധനം 2 ന്റെയും ബണ്ടിലുകളാണ്. ഈ ബണ്ടിലിനെ കാര്യക്ഷമമായ ബണ്ടിൽ എന്നു വിളിക്കുന്നു.

2 ) ബജറ്റ് ലൈനിന്റെ താഴെയുള്ള ഏതൊരു ബിന്ദുവും സൂചിപ്പിക്കുന്നത് ഒരു ഉപഭോക്താവിന് അദ്ദേഹത്തിന്റെ വരുമാനം പൂർണ്ണമായും ഉപയോഗിക്കാതെ വാങ്ങുന്ന സാധനം 1 ന്റെയും സാധനം 2 ന്റെയും ബണ്ടിലുകളാണ്. ഇതിനെ മേന്മ കുറഞ്ഞ ബണ്ടിലുകൾ എന്നു പറയുന്നു.

3 ) ബജറ്റ് ലൈനിന്റെ മുകളിലുള്ള ഏതൊരു ബിന്ദുവും സൂചിപ്പിക്കുന്നത് ഒരു ഉപഭോക്താവിന് അദ്ദേഹത്തിന്റെ പരിമിതമായ വരുമാനം കൊണ്ട് വാങ്ങുവാൻ സാധിക്കാത്ത സാധനം 1 ന്റെയും സാധനം 2 ന്റെയും ബണ്ടിലുകളാണ്. ഇതിനെ മേന്മ കൂടിയ ബണ്ടിലുകൾ എന്നു പറയുന്നു.

ബജറ്റ് സെറ്റിലെ മാറ്റങ്ങൾ ( Changes in Budget Set )
ഒരു ഉപഭോക്താവിന് ലഭ്യമായ ഉപഭോഗ ബണ്ടിലുകൾ സാധനങ്ങളുടെ ( i ) വിലകളെയും ( ii ) ഉപഭോക്താവിന്റെ വരുമാനത്തെയും ആശ്രയിച്ചിരിക്കുന്നു. അതുകൊണ്ട് സാധനങ്ങളുടെ വിലയിലോ വരുമാനത്തിലോ മാറ്റമുണ്ടായാൽ ബജറ്റ് സെറ്റിലും ബജറ്റ് രേഖയിലും മാറ്റങ്ങൾ ഉണ്ടാകും.

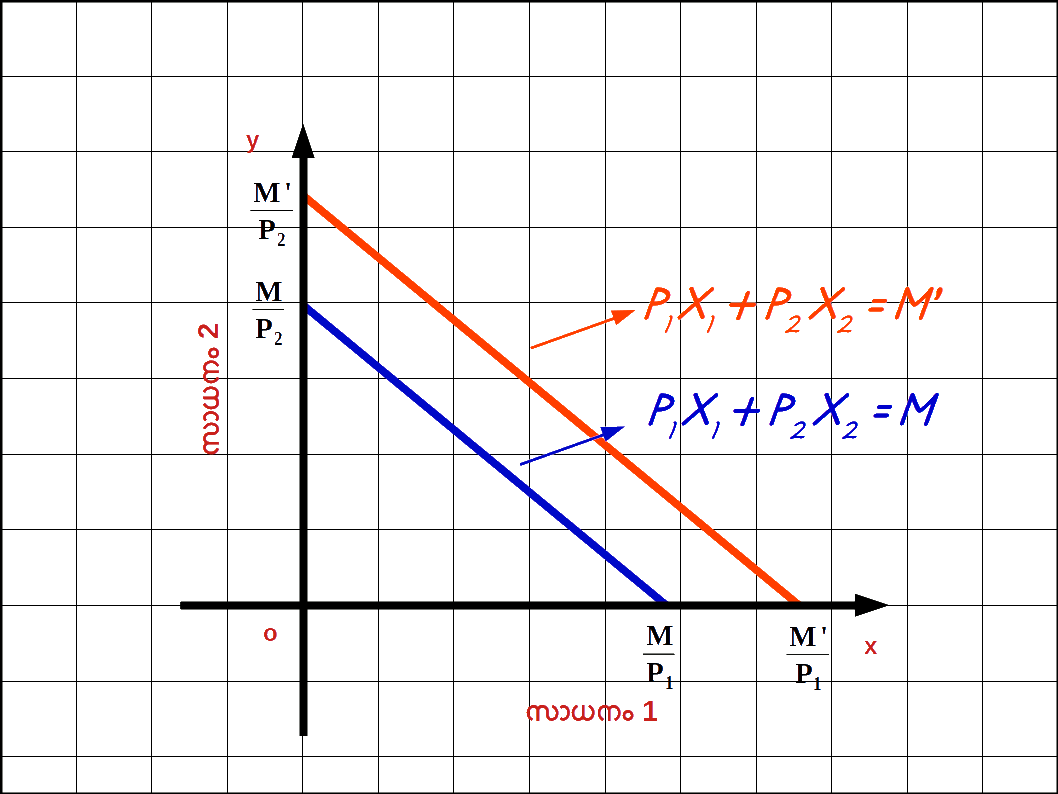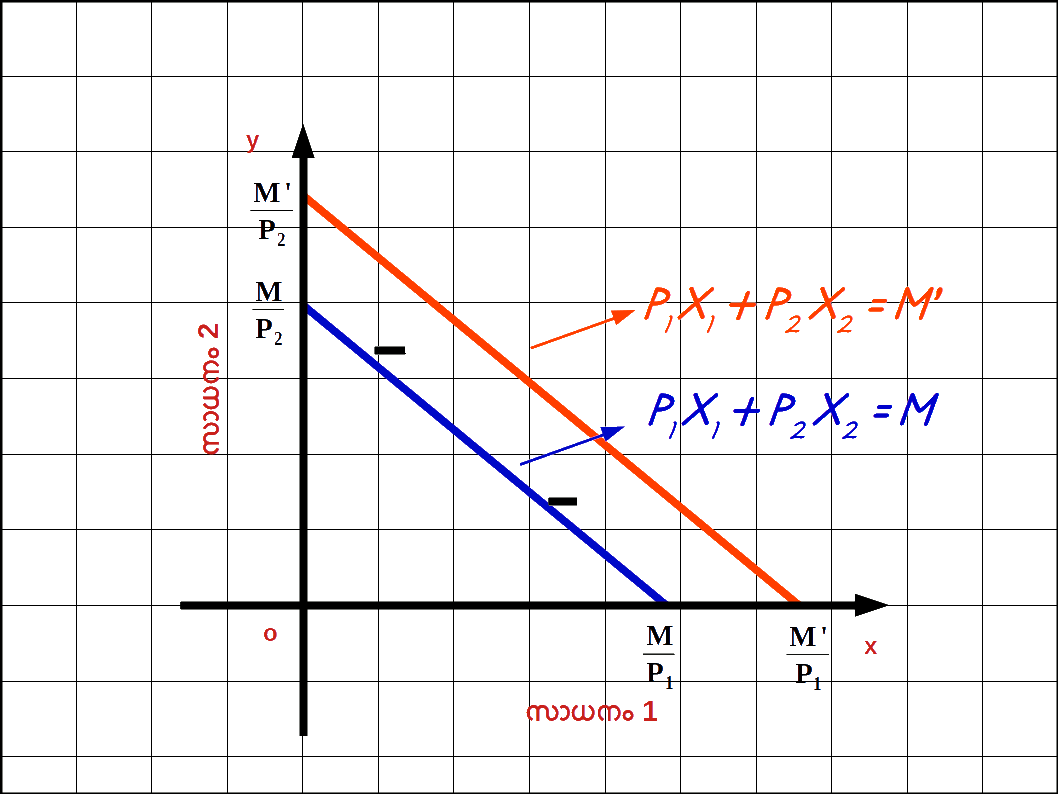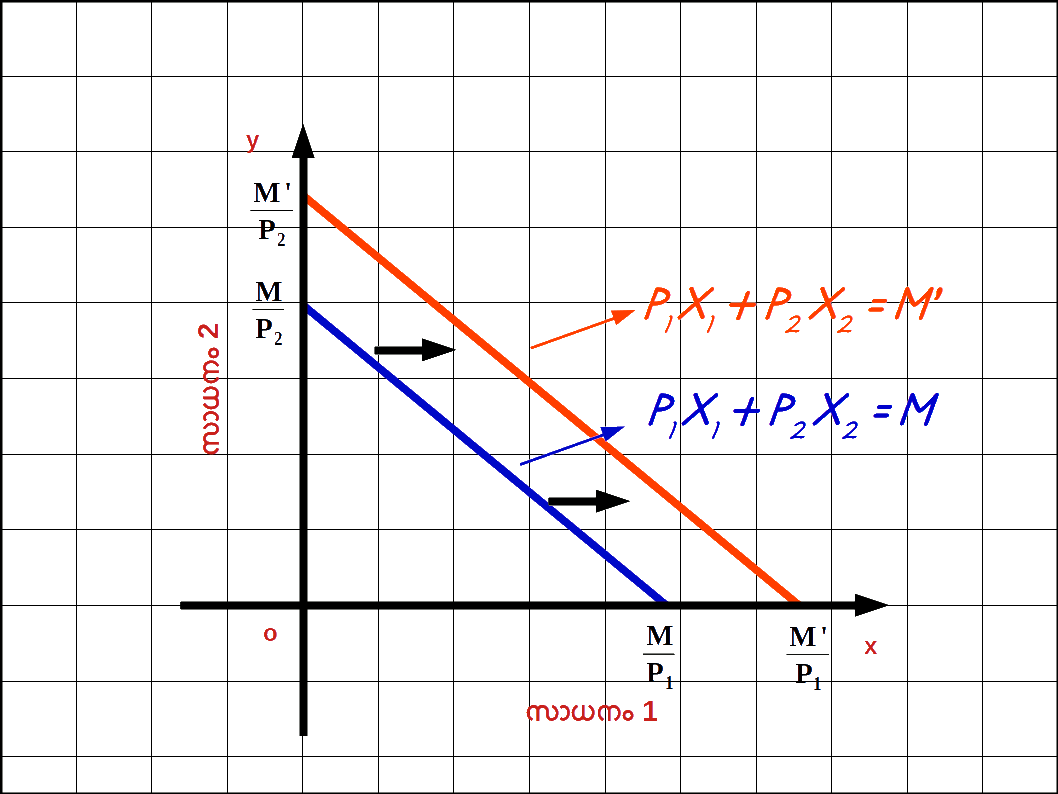
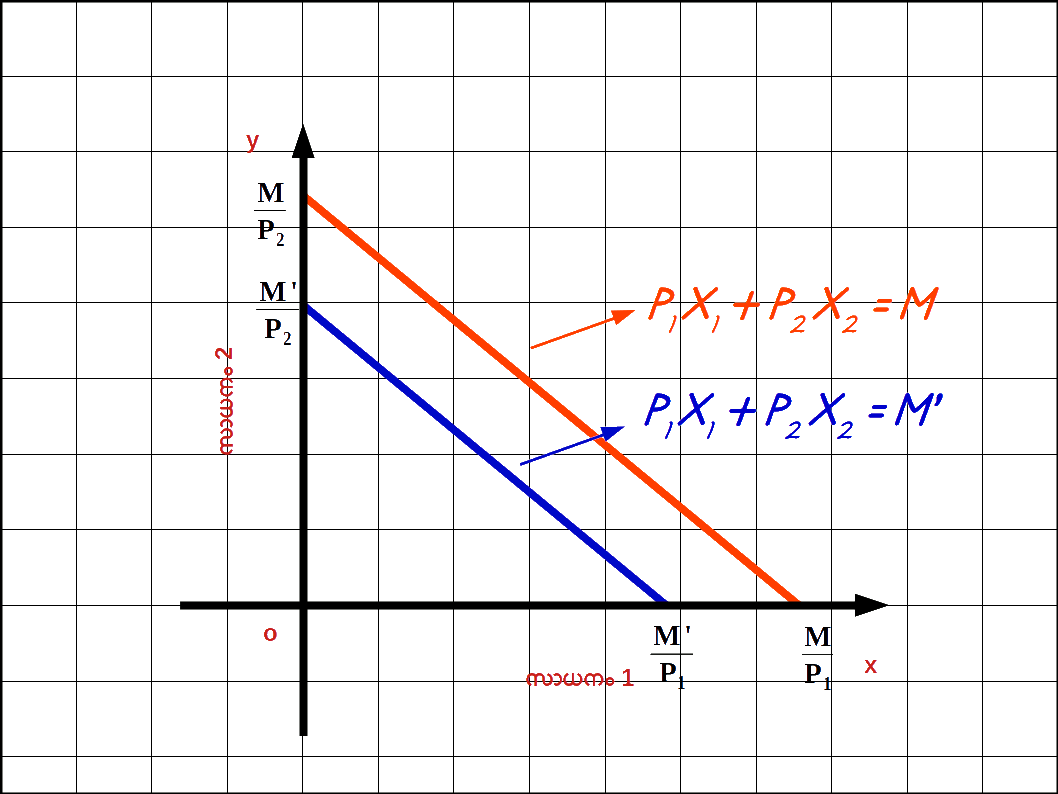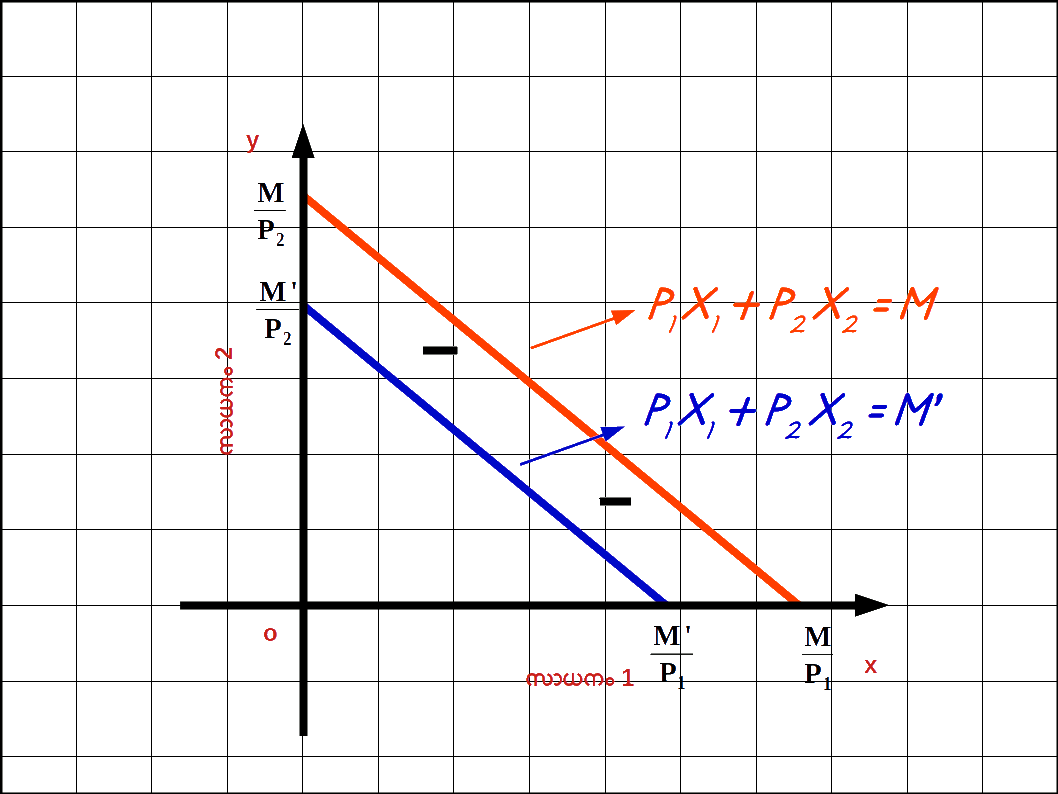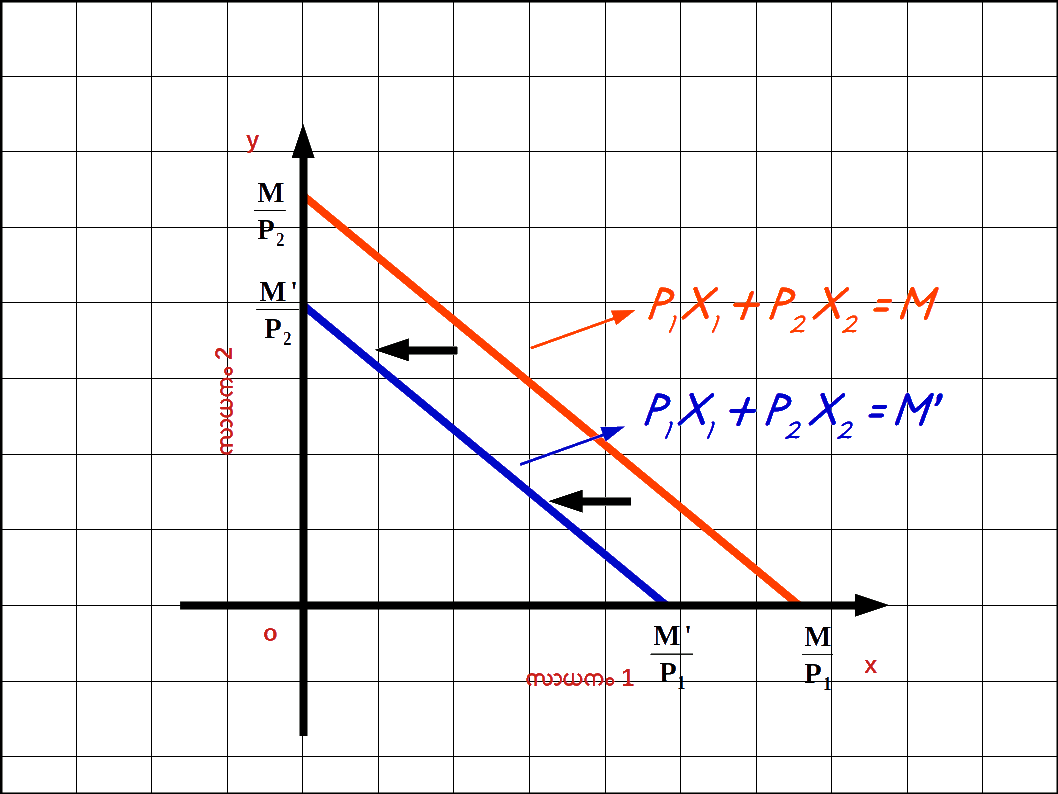
വരുമാനം വർദ്ധിച്ചാൽ :
ഉപഭോക്താവിന്റെ വരുമാനം M ൽ നിന്ന് M’ ആയി വർദ്ധിച്ചാൽ ബജറ്റ് രേഖ വലത്തോട്ട് സ്ഥാനം മാറുന്നു. പുതിയ ബജറ്റ് രേഖ സമവാക്യം : P₁x₁ + P₂x₂ = M ‘ എന്നാകുന്നു. ഈ ബജറ്റ് രേഖയുടെ വെർട്ടിക്കൽ ഇന്റർസെപ്റ്റ് $ \mathbf {{{{{\frac{M’}{P_2}}} }}} $ ഉം ഹൊറിസോണ്ടൽ ഇന്റർസെപ്റ്റ് $ \mathbf {{{{{\frac{M’}{P_1}}} }}} $ ആണ് . വരുമാനം M ഉം M’ ഉം ആകുമ്പോഴുള്ള ബജറ്റ് രേഖകൾ ഡയഗ്രം 2.7 ൽ കൊടുത്തിരിക്കുന്നു.

Diagram 2.7

ഉപഭോക്താവിന്റെ വരുമാനം വർധിച്ചതിന്റെ ഫലമായി ഉപഭോക്താവിന് രണ്ട് സാധനങ്ങളും കൂടുതൽ വാങ്ങുവാൻ കഴിയുന്നു. പുതിയ ബജറ്റ് പഴയ ബജറ്റ് ലൈനിന് സമാന്തരമായി വലതുഭാഗത്തേക്ക് മാറുന്നു.
ഉപഭോക്താവിന്റെ വരുമാനം 20 യിൽ നിന്ന് 30 യായി വർധിക്കുകയും സാധനം 1 ന്റെയും സാധനം 2 ന്റെയും വിലകൾ മാറ്റമില്ലാതെ 5 യായി തുടരുകയും ചെയ്യുന്നുവെന്ന് കരുതുക. അപ്പോൾ പുതിയ ബജറ്റ് രേഖ സമവാക്യം : 5x₁ + 5x₂ = 30 എന്നാകും. ഇവിടെ വെർട്ടിക്കൽ ഇന്റർസെപ്റ്റം ഹൊറിസോണ്ടൽ ഇന്റർസെപ്റ്റം 6 ആണ്. വരുമാനം 20 രൂപയിൽ നിന്ന് 30 യായി വർധിച്ചപ്പോൾ വെർട്ടിക്കൽ ഇന്റർസെപ്റ്റുകൾ 4 ൽ നിന്ന് 6 ലേക്ക് നീങ്ങിയിരിക്കുന്നത് ഗ്രാഫ് 2.8 ൽ കാണാൻ കഴിയും. തന്മൂലം 5x₁ + 5x₂ = 20 എന്ന ബജറ്റ് രേഖ 5x₁ + 5x₂ = 30 എന്ന ബജറ്റ് രേഖയായി വലതു ഭാഗത്തേക്ക് നീങ്ങിയിരിക്കുന്നു.

Diagram 2.8

ഇപ്പോൾ ഉപഭോക്താവിന് രണ്ടു സാധനങ്ങളും കൂടുതൽ വാങ്ങുവാൻ കഴിയുന്നു. ബജറ്റ് രേഖകളുടെ ചെരിവ് -1 തന്നെയാണ്.
Problem 2.4: P₁ = 2 , P₂ = 4 , M = 16 ആയാൽ ( 1) ബജറ്റ് രേഖ സമവാക്യം എഴുതുക. ( 2 ) വെർട്ടിക്കൽ ഇന്റർസെപ്റ്റ് എത്രയാണ് ? ( 3) ഹൊറിസോണ്ടൽ ഇന്റർസെപ്റ്റ് എത്രയാണ് ? ( 4 ) ബജറ്റ് രേഖയുടെ ചെരിവ് എത്രയാണ് ? ( 5 ) ബജറ്റ് രേഖ വരയ്ക്കുക ( 6 ) M = 16 ൽ നിന്ന് M’ = 20 ആയാൽ ബജറ്റ് രേഖയ്ക്ക് എന്തു സംഭവിക്കും ? വരയ്ക്കുക ( 7 ) പുതിയ ബജറ്റ് ലൈനിന്റെ ചെരിവ് എത്രയാണ് ?
Solution :

( 1 ) 2x₁ + 4x₂ = 16

( 2 ) വെർട്ടിക്കൽ ഇന്റർസെപ്റ്റ് $ \mathbf {{{\frac{M}{P_2}}} } $ = $ \mathbf {{{{{\frac{16}{4}}} }}} $ = 4

( 3 ) ഹൊറിസോണ്ടൽ ഇന്റർസെപ്റ്റ് $ \mathbf {{{{{\frac{M}{P_1}}} }}} $ = $ \mathbf {{{{{\frac{16}{2}}} }}} $ = 8

( 4 ) ചെരിവ് $ \mathbf {{{{{\frac{Δx_{2}}{Δx_{1}}}} }}} $ = – $ \mathbf {{{{{\frac{P_{1}}{P_{2}}}} }}} $ = – $ \mathbf {{{{{\frac{2}{4}}} }}} $ = – $ \mathbf {{{{{\frac{1}{2}}} }}} $ = – 0.5

( 5 )

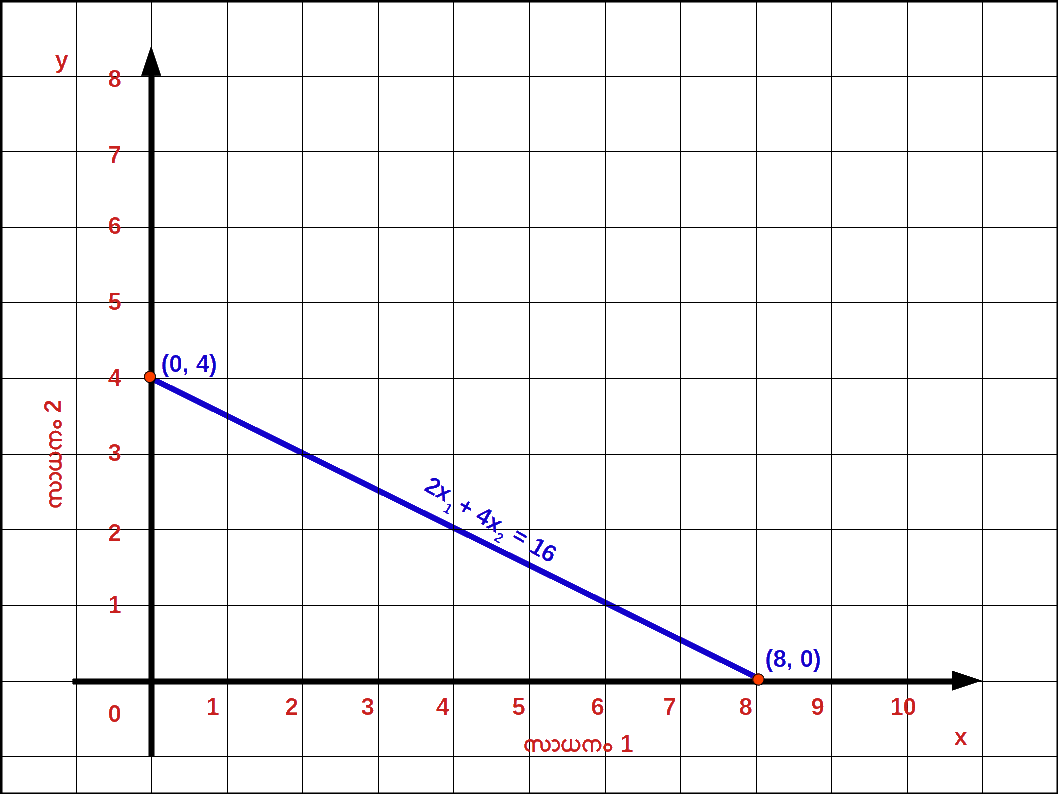
( 6 ) പുതിയ ബജറ്റ് രേഖ വലതുഭാഗത്തേക്ക് മാറിയിരിക്കുന്നു

( 7 ) – $ \mathbf {{{{{\frac{P_{1}}{P_{2}}}} }}} $ = – $ \mathbf {{{{{\frac{2}{4}}} }}} $ = – $ \mathbf {{{{{\frac{1}{2}}} }}} $ = – 0.5

വരുമാനം കുറഞ്ഞാൽ :
അതുപോലെ ഉപഭോക്താവിന്റെ വരുമാനം കുറയുമ്പോൾ നേരത്തെ വാങ്ങിയിരുന്ന അതേ അളവിൽ സാധനം വാങ്ങാൻ കഴിയാതെ വരുന്നു. അപ്പോൾ ബജറ്റ് രേഖ അകത്തേക്ക് ( ഇടതുഭാഗത്തേക്ക് ) സ്ഥാനം മാറുന്നു. അതായത് വരുമാനം M ൽ നിന്ന് M’ ആയി കുറയുമ്പോൾ (M’ < M) ബജറ്റ് രേഖ ഇടത്തോട്ട് നീങ്ങുന്നു. ഇത് ഡയഗ്രം 2.9 ൽ കൊടുത്തിരിക്കുന്നു.

Diagram 2.9

PROBLEM 2.5 : 3x₁ + 4x₂ = 12 എന്ന ബജറ്റ് രേഖയും 3x₁ + 4x₂ = 20 എന്ന ബജറ്റ് രേഖയും തമ്മിലുള്ള വ്യത്യാസം എന്ത് ?. രണ്ട് ബജറ്റ് രേഖകളുടെ ചെരിവ് കണ്ടുപിടിച്ച് താരതമ്യം ചെയ്യുക.
Solution :
ഒന്നാമത്തെ ബജറ്റ് രേഖയിൽ വരുമാനം 12 രൂപയും രണ്ടാമത്തെ ബജറ്റ് രേഖയിൽ വരുമാനം 20 രൂപയുമാണ്. ഒന്നാമത്തെ ബജറ്റ് രേഖയുടെ ചെരിവും രണ്ടാമത്തെ ബജറ്റ് രേഖയുടെ ചെരിവും തുല്യമാണ്. അതായത് , $ \mathbf {{{{{\frac{P_{1}}{P_{2}}}} }}} $ = – $ \mathbf {{{{{\frac{3}{4}}} }}} $ ആണ് ചെരിവ്. രണ്ട് സാധനങ്ങളുടെയും വിലയിൽ മാറ്റമില്ലാത്തതുകൊണ്ടാണ് ഇങ്ങനെ സംഭവിക്കുന്നത്.

വിലയിലുണ്ടാകുന്ന മാറ്റം ( Changes in Price )
ഉപഭോക്താവിന്റെ വരുമാനത്തിൽ മാറ്റമില്ലാതെ സാധനങ്ങളുടെ വിലകളിൽ മാറ്റം ഉണ്ടായാൽ വെർട്ടിക്കൽ – ഹൊറിസോണ്ടൽ ഇന്റർസെപ്റ്റുകളിലും ചെരിവിലും മാറ്റമുണ്ടാകും.

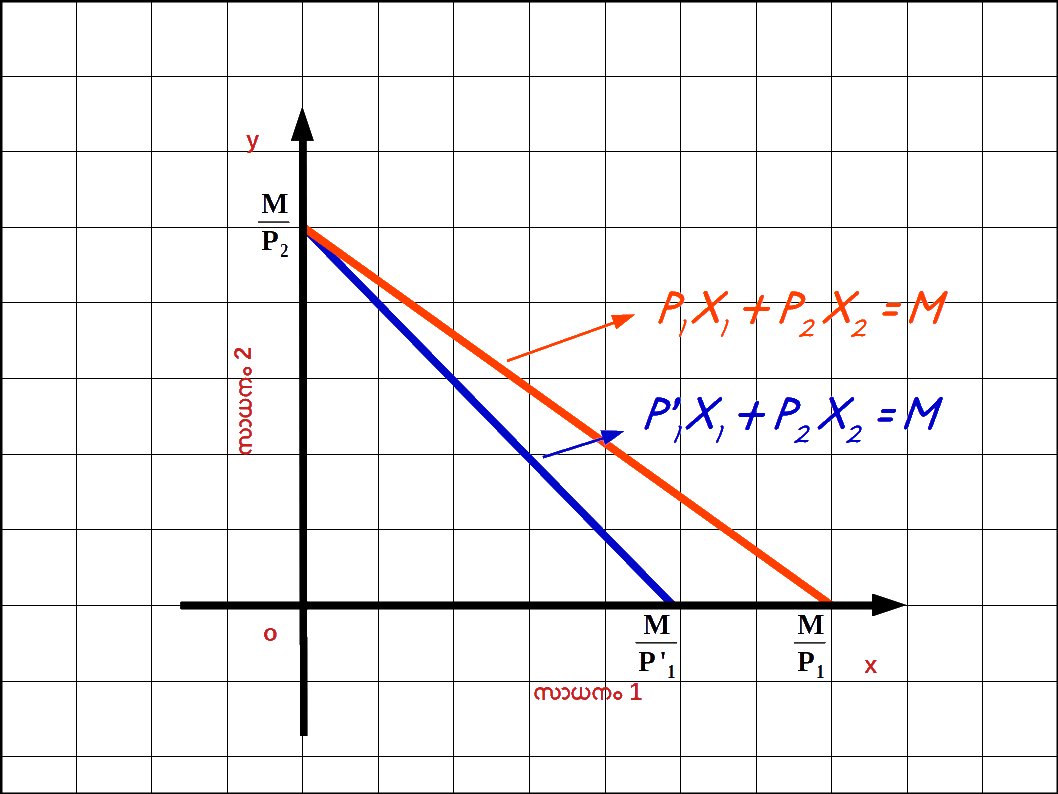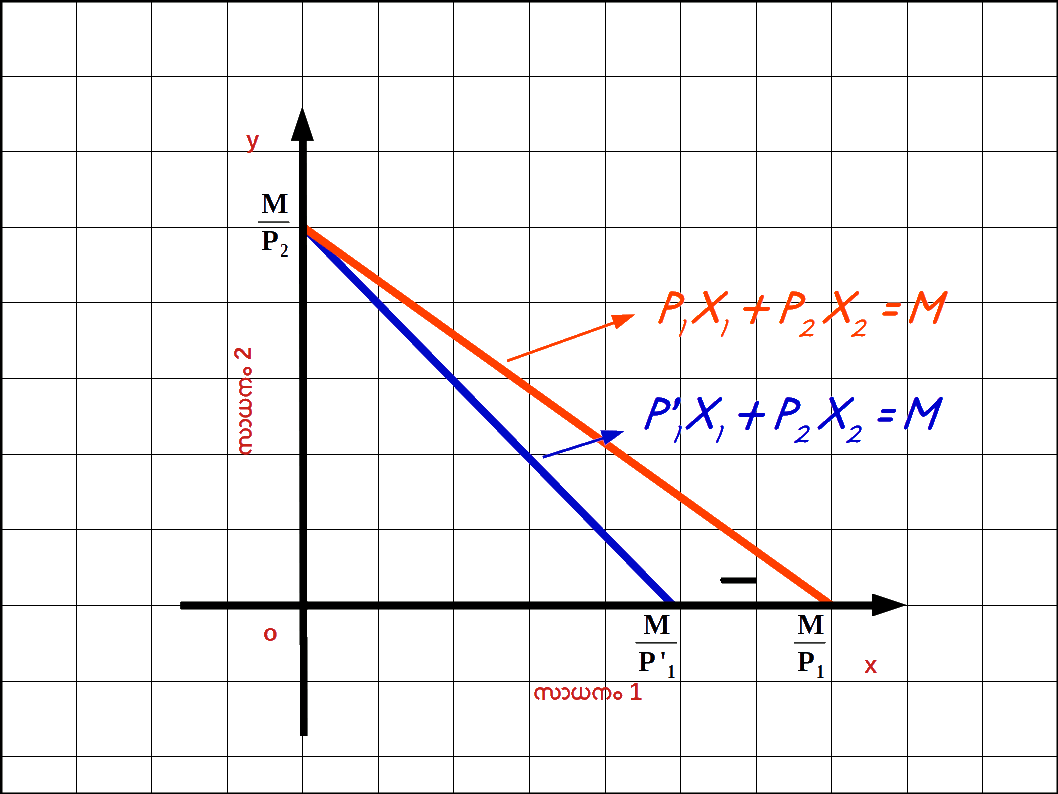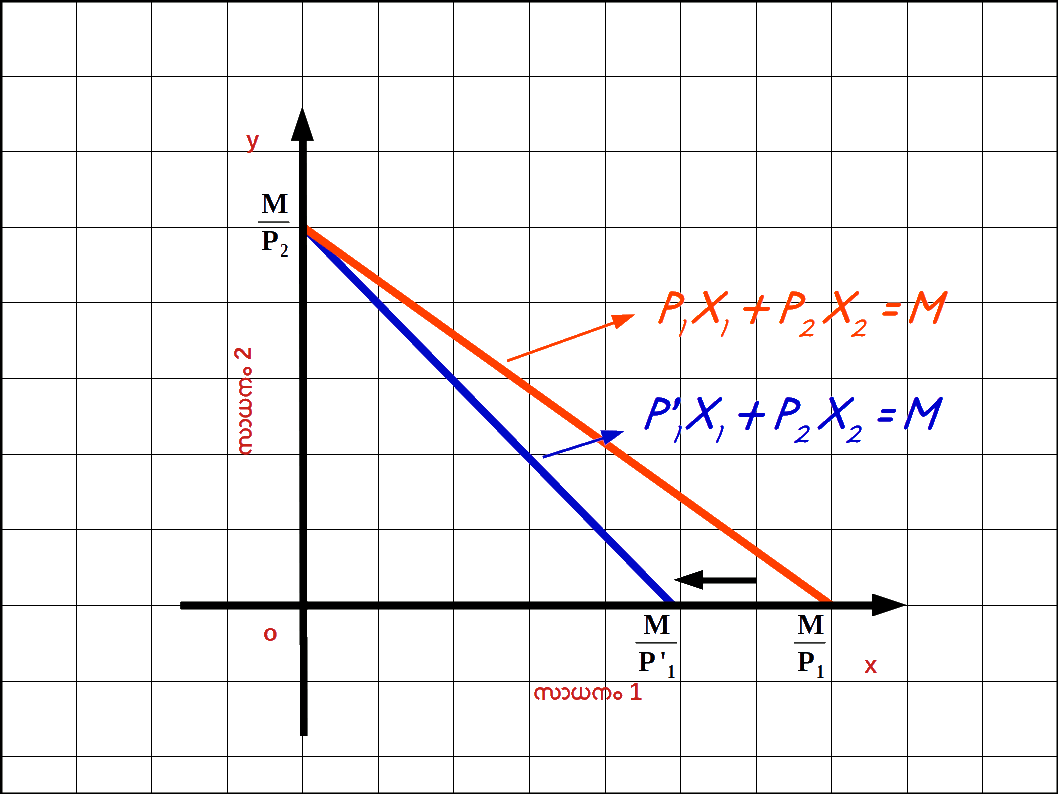
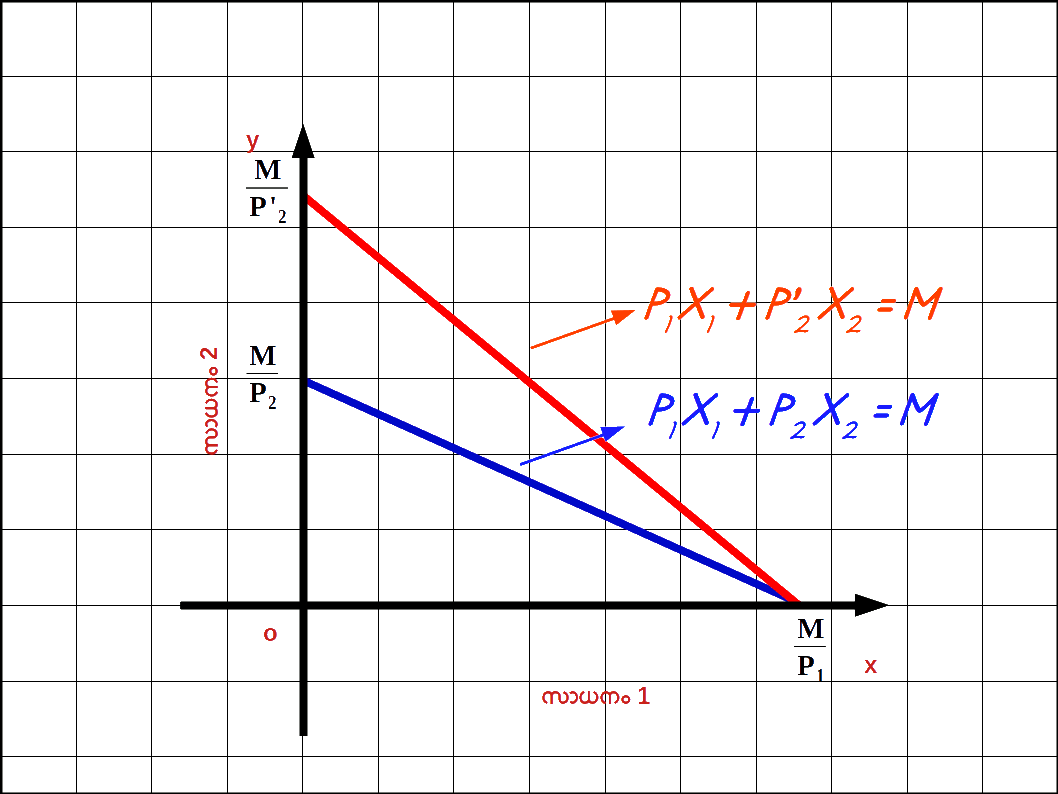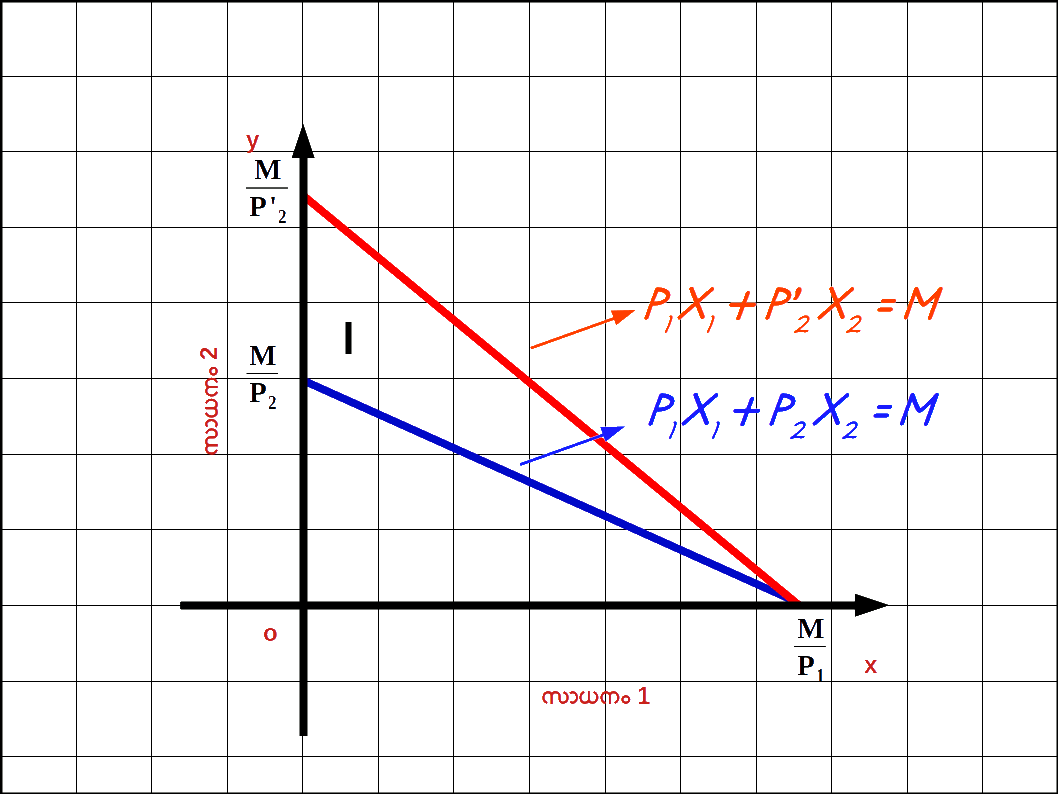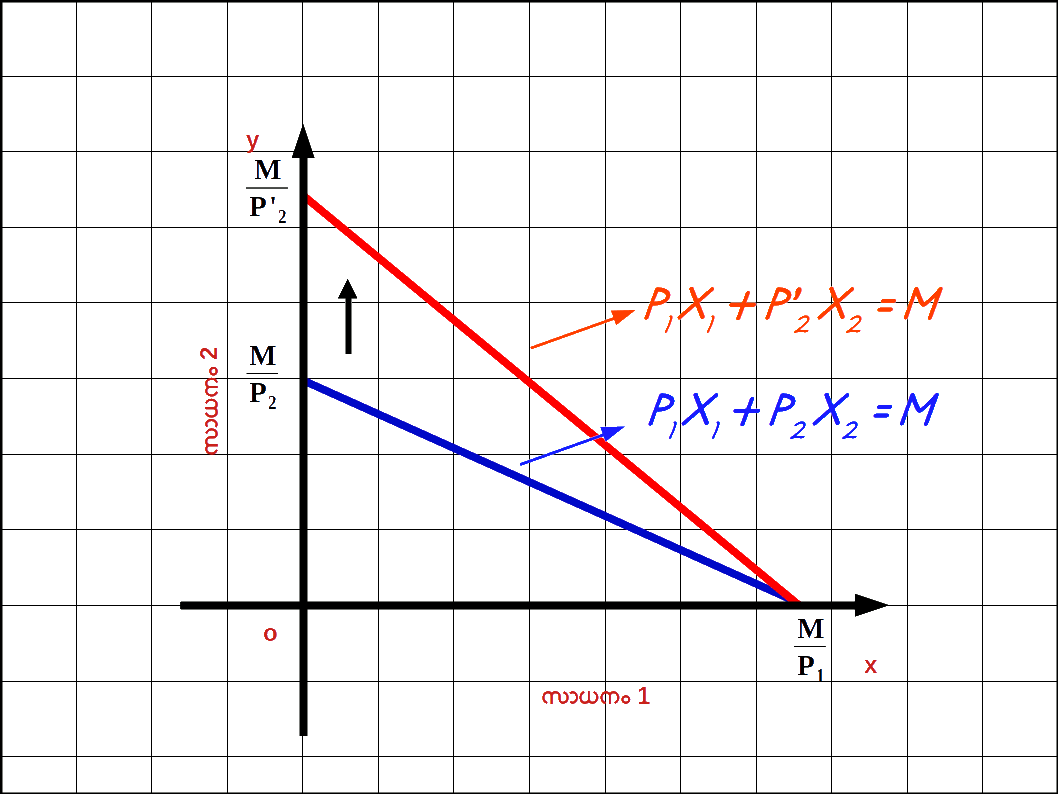
സാധനം 1 ന്റെ വില വർധിച്ചാൽ :
സാധനം 1 ന്റെ വില നിന്ന് P₁ P’₁ ലേക്ക് വർധിക്കുകയും ( P’₁ > P₁ ) സാധനം 2 ന്റെ വിലയിലും വരുമാനത്തിലും മാറ്റമില്ലാതിരിക്കുകയും ചെയ്യുമ്പോൾ ബജറ്റ് രേഖയുടെ ഹൊറിസോണ്ടൽ ഇന്റർസെപ്റ്റ് y അക്ഷത്തിന് അടുത്തേക്ക് മാറുകയും ചെരിവ് കൂടുകയും ചെയ്യും. P’₁x₁ + P₂x₂ = M എന്നത് സാധനം 1 ന്റെ വില P₁ ൽ നിന്ന് P’₁ ആയി വർധിച്ചപ്പോഴുള്ള ബജറ്റ് ലൈൻ സമവാക്യമാണ് . ഇവിടെ $ \mathbf {{{{{\frac{M}{P_2}}} }}} $ വെർട്ടിക്കൽ ഇന്റർസെപ്റ്റം $ \mathbf {{{{{\frac{M}{P’_1}}} }}} $ ഹൊറിസോണ്ടൽ ഇന്റർസെപ്റ്റമാണ്. – $ \mathbf {{{{{\frac{P’_{1}}{P_{2}}}} }}} $ ബജറ്റ് രേഖയുടെ ചെരിവുമാണ്. രണ്ട് ബജറ്റ് രേഖകളും ഡയഗ്രം 2.10 ൽ കൊടുത്തിരിക്കുന്നു. ഒന്നാമത്തെ സാധനത്തിന്റെ വില വർധിച്ചതുമൂലം ഹൊറിസോണ്ടൽ ഇന്റർസെപ്റ്റ് $ \mathbf {{{{{\frac{M}{P_1}}} }}} $ ൽനിന്ന് $ \mathbf {{{{{\frac{M}{P’_1}}} }}} $ ആയി അകത്തേക്ക് മാറിയിരിക്കുന്നത് കാണാം. മാത്രമല്ല , വെർട്ടിക്കൽ ഇന്റർസെപ്റ്റിൽ മാറ്റമില്ല. അത് $ \mathbf {{{{{\frac{M}{P_2}}} }}} $ തന്നെ ആണ്.

Diagram 2.10

EXAMPLE 2.8 : സാധനം 1 ന്റെ വില 5 യിൽനിന്ന് 10 യായി വർധിക്കുകയും സാധനം 2 ന്റെ വില 5 യും ഉപഭോക്താവിന്റെ വരുമാനം 20 യുമാണെങ്കിൽ പുതിയ ബജറ്റ് രേഖ 10x₁ + 5x₂ = 20 എന്നായിരിക്കും. വെർട്ടിക്കൽ ഇന്റർസെപ്റ്റ് 4 ഉം $\biggl({\frac{M}{P_2}}\, = \,{\frac{20}{5}} \,=\, 4 \biggr)$ ഹൊറിസോണ്ടൽ ഇന്റർസെപ്റ്റ് 2 ഉം $\biggl({\frac{M}{P’_1}}\, = \,{\frac{20}{10}} \,=\, 2 \biggr)$ ആയിരിക്കും. ബജറ്റ് രേഖയുടെ ചെരിവ് -2 ആണ്. എന്തുകൊണ്ടെന്നാൽ ഒരു യൂണിറ്റ് സാധനം 1 ലഭിക്കാൻ സാധനം 2 ന്റെ രണ്ട് യൂണിറ്റ് ത്യജിക്കേണ്ടി വരുന്നു. ഗ്രാഫ് 2.11 ൽ 5x₁ + 5x₂ = 20 പഴയ ബജറ്റു ലൈനും 10x₁ + 5x₂ = 20 പുതിയ ബജറ്റു ലൈനുമാണ്. പുതിയ ബജറ്റ് ലൈനിന്റെ ഹൊറിസോണ്ടൽ ഇന്റർസെപ്റ്റ് വെർട്ടിക്കൽ അക്ഷത്തിന് അടുത്തേക്ക് നീങ്ങിയിരിക്കുന്നത് കാണാം.

Diagram 2.11

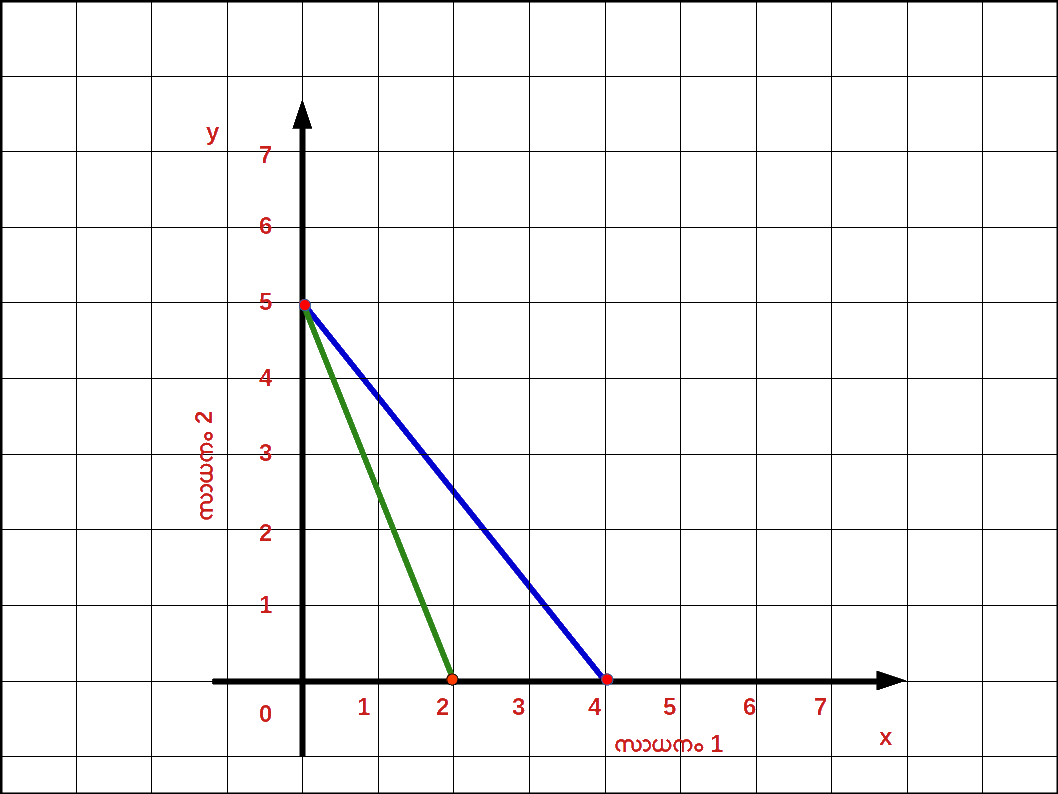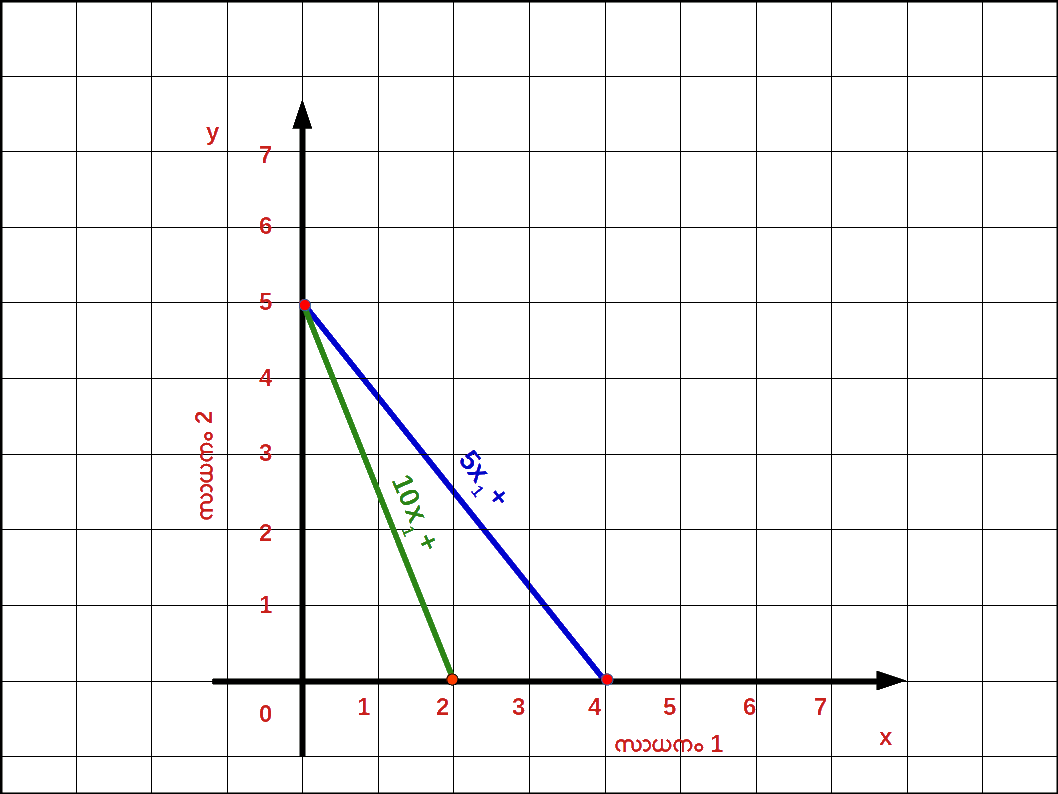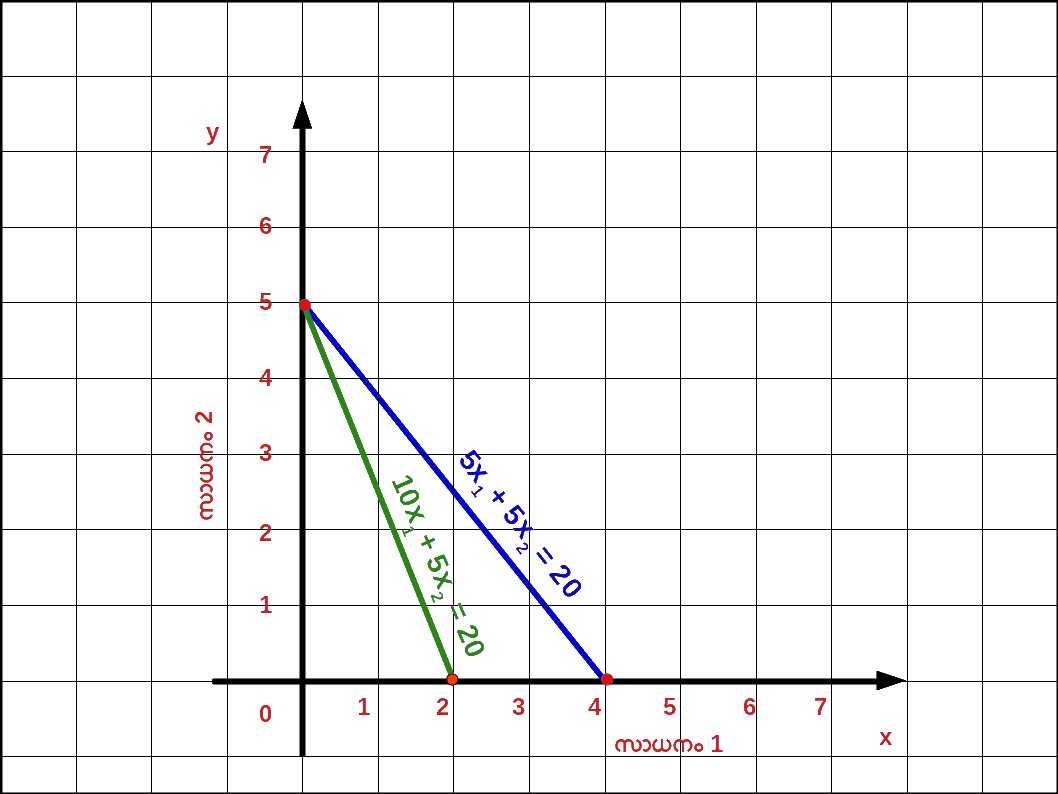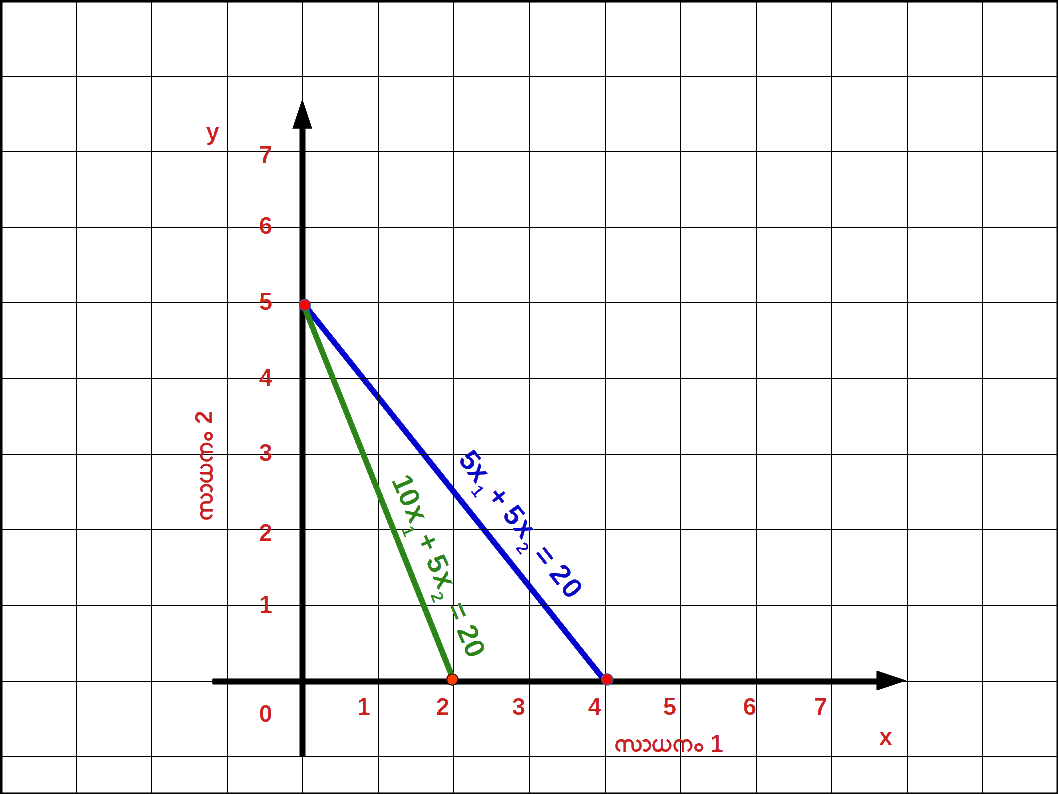
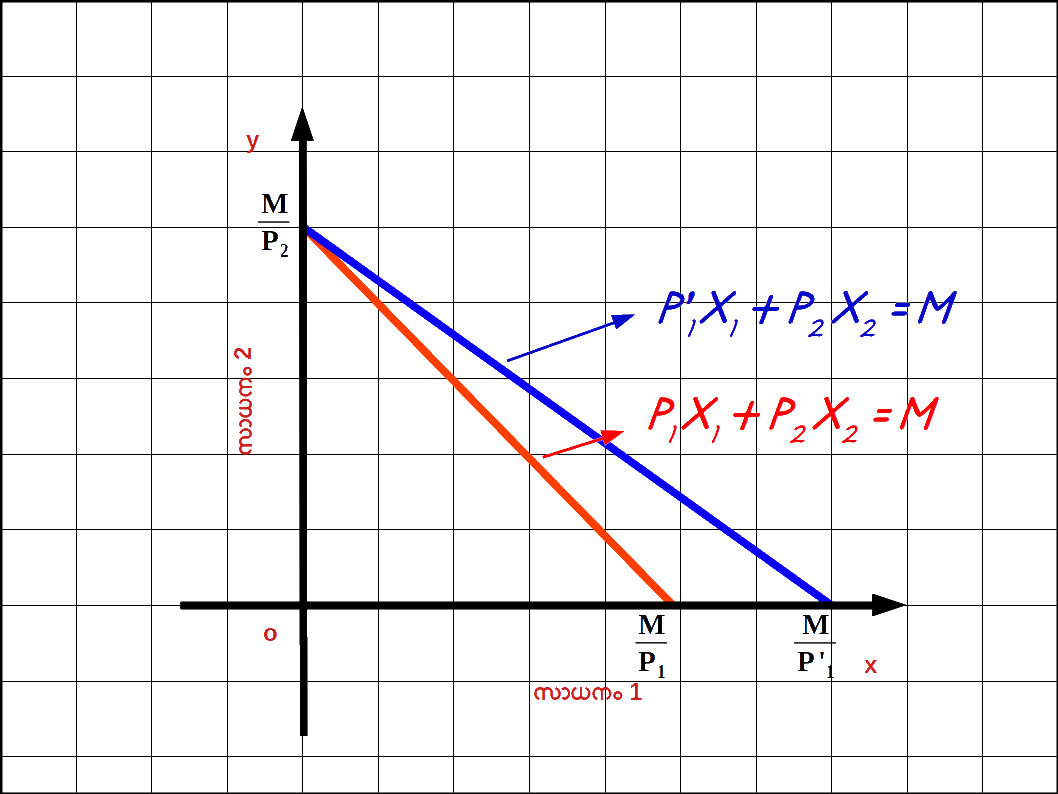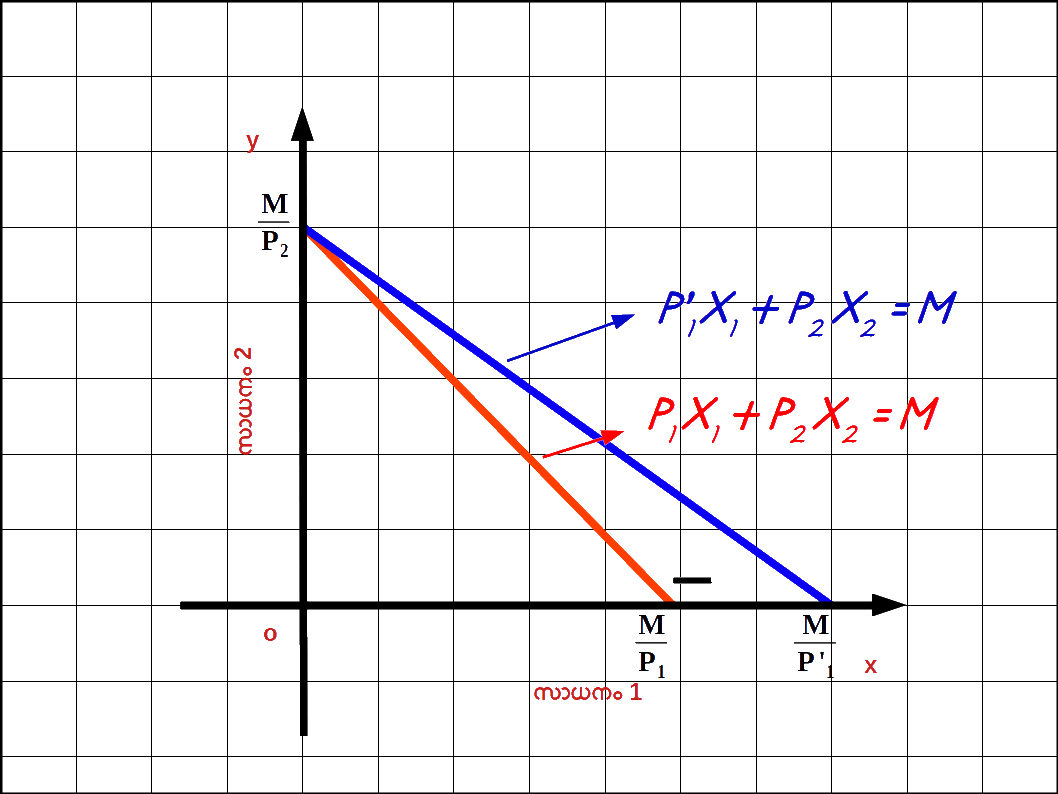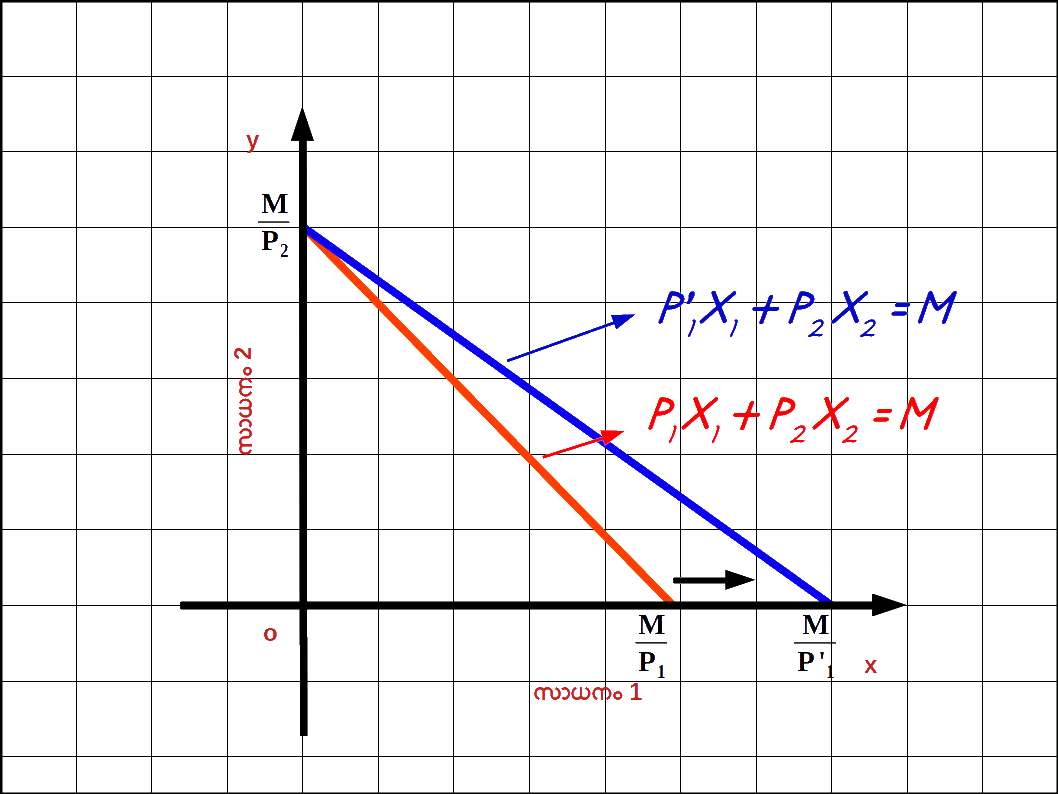
സാധനം 1 ന്റെ വില കുറഞ്ഞാൽ :
സാധനം 2 ന്റെ വിലയും വരുമാനവും മാറ്റമില്ലാതിരിക്കുകയും സാധനം 1 ന്റെ വില P₁ ൽ നിന്ന് P’₁ ലേക്ക് കുറഞ്ഞാൽ ബജറ്റ് രേഖയുടെ ഹൊറിസോണ്ടൽ ഇന്റർസെപ്റ്റ് വെർട്ടിക്കൽ അക്ഷത്തിൽ നിന്ന് പുറത്തേക്ക് നീങ്ങുന്നു. കൂടാതെ ബജറ്റ് രേഖയുടെ ചെരിവ് കുറയുന്നു. ഈ സാഹചര്യം ഡയഗ്രം 2.12 ൽ കൊടുത്തിരിക്കുന്നു. സാധനം 1 ന്റെ വില കുറയുമ്പോൾ ഉപഭോക്താവിന് ആ സാധനത്തിന്റെ കൂടുതൽ യൂണിറ്റ് വാങ്ങുവാൻ കഴിയുന്നു.

Diagram 2.12

EXAMPLE 2.9 ; 5x₁ + 5x₂ = 20 എന്ന ബജറ്റ് ലൈൻ സമവാക്യത്തിൽ സാധനം 1 ന്റെ വില 5 ൽ നിന്ന് 4 യായി കുറഞ്ഞാൽ 4x₁ + 5x₂ = 20 എന്ന പുതിയ ബജറ്റ് രേഖയുടെ വെർട്ടിക്കൽ ഇന്റർസെപ്റ്റ് 4 ഉം M 20 $\biggl({\frac{M}{P_2}}\, = \,{\frac{20}{5}} \,=\, 4 \biggr)$ ഹൊറിസോണ്ടൽ ഇന്റർസെപ്റ്റ് 4 ൽനിന്ന് 5 ആയി വർധിക്കുന്നു $\biggl({\frac{M}{P’_1}}\, = \,{\frac{20}{4}} \,=\, 5 \biggr)$. 5. ബജറ്റ് രേഖയുടെ ചെരിവ് 1 എന്നത് 0.8 ആകുന്നു $\biggl(-\,{\frac{P’_1}{P_2}}\, = \,{-\,\frac{4}{5}} \,=\,-\, .08 \biggr)$.

Diagram 2.13

ഗ്രാഫ് 2.13 ൽ ബജറ്റ് രേഖകൾ വരച്ചിരിക്കുന്നത് പരിശോധിക്കുക.

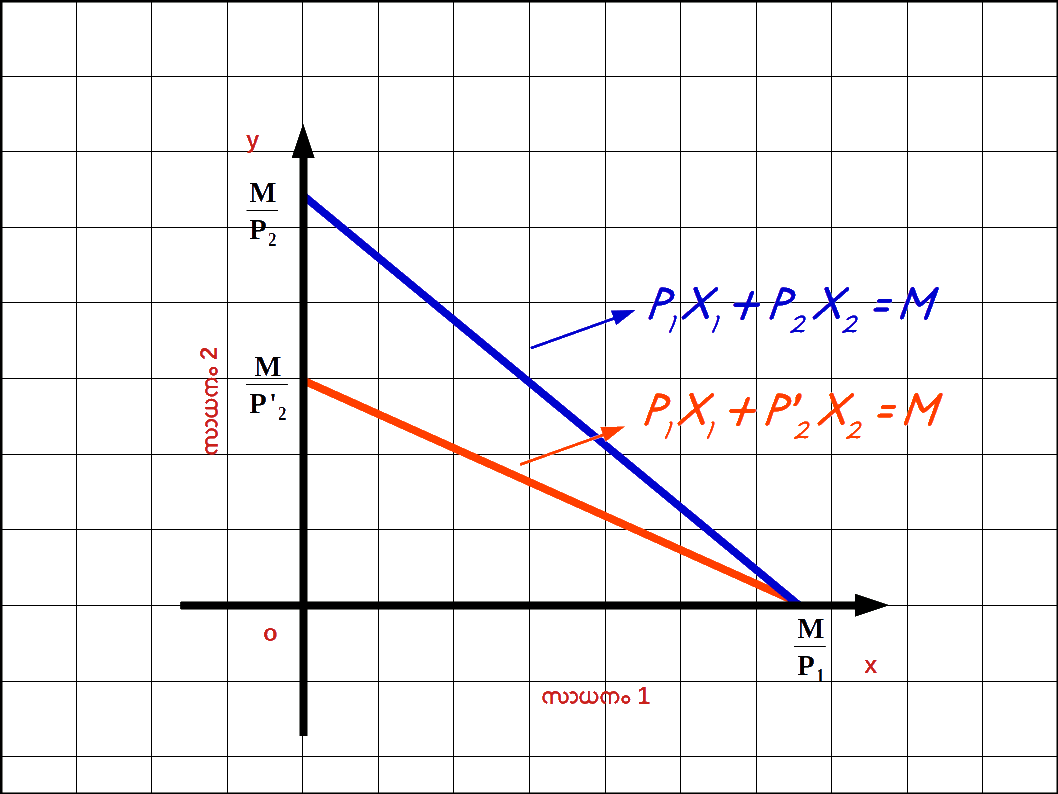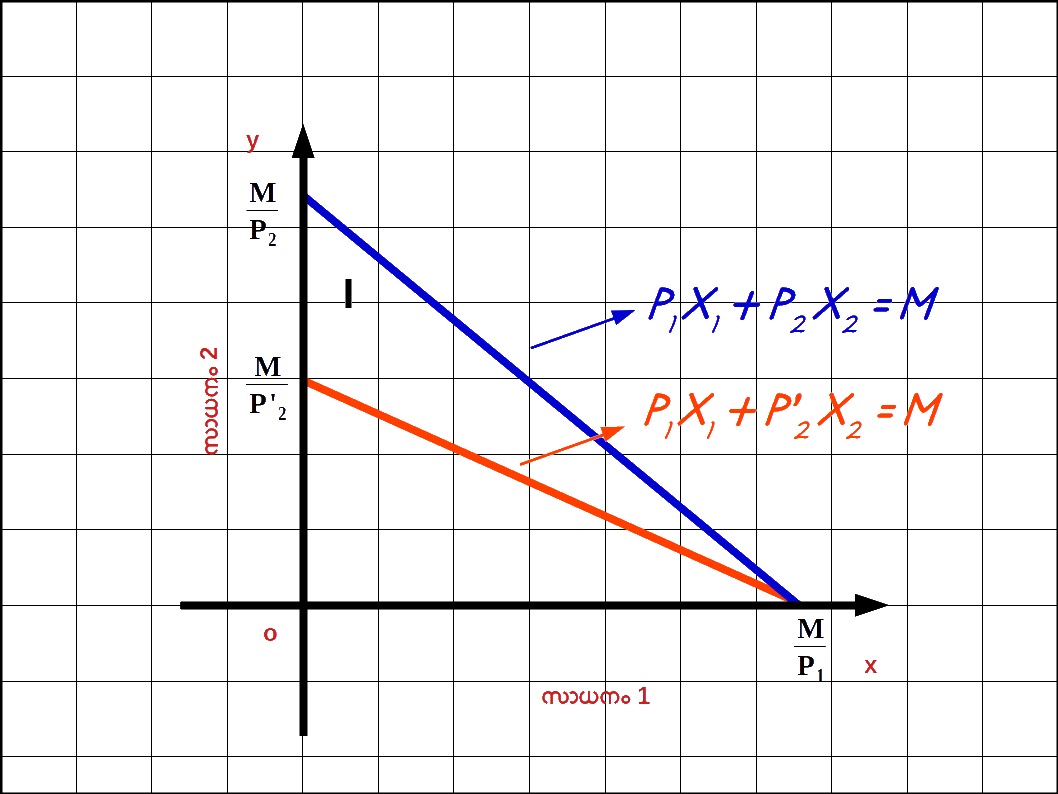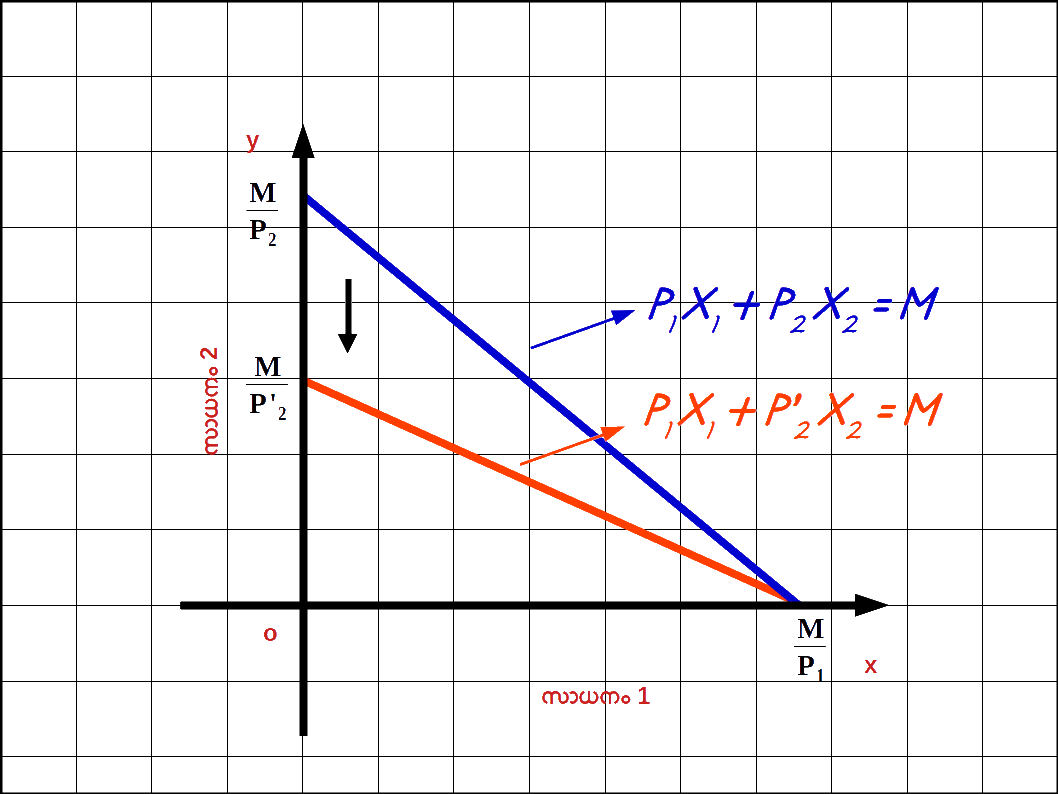
സാധനം 2 ന്റെ വിലയിൽ മാറ്റം :
സാധനം 1 ന്റെ വിലയിലും ഉപഭോക്താവിന്റെ വരുമാനത്തിലും മാറ്റ മില്ലാതെ , സാധനം 2 ന്റെ വിലയിൽ മാറ്റമുണ്ടായാൽ ബജറ്റ് സെറ്റിനും ബജറ്റ് രേഖയ്ക്കും ചെരിവിനും മാറ്റ മുണ്ടാകുന്നു.

സാധനം 2 ന്റെ വില വർധിച്ചാൽ :
സാധനം 2 ന്റെ വില വർധിച്ചാൽ ( P’₂ > P₂ ) ബജറ്റ് രേഖയുടെ വെർട്ടിക്കൽ ഇന്റർസെപ്റ്റ് x – അക്ഷത്തിന് അടുത്തേക്ക് നീങ്ങുകയും ചെരിവ് കുറയുകയും ചെയ്യുന്നു.

Diagram 2.14

സാധനം 2 ന്റെ വില കുറഞ്ഞാൽ :
നേരെ മറിച്ച് സാധനം 2 ന്റെ വില കുറഞ്ഞാൽ ബജറ്റ് രേഖയുടെ ( P’₂ > P₂ ) വെർട്ടിക്കൽ ഇന്റർസെപ്റ്റ് y – അക്ഷത്തിൽനിന്ന് പുറത്തേക്ക് മാറുകയും ചെരിവ് വർധിക്കുകയും ചെയ്യുന്നു . ഡയഗ്രം 2.15 ൽ ഇത് വരച്ചിരിക്കുന്നത് കാണുക.

Diagram 2.15

PROBLEM 2.6 : ഒരു ഉപഭോക്താവിന്റെ വരു മാനം 100 യും സാധനം 1 ന്റെ വില 10 യും സാധനം 2 ന്റെ വില 20 യുമാണ്. താഴെ കൊടുത്തിരിക്കുന്ന ചോദ്യങ്ങൾക്ക് ഉത്തരം എഴുതുക.

1. ഉപഭോക്താവിന്റെ ബജറ്റ് എത്രയാണ് ?

2. ബജറ്റ് സെറ്റ് സമവാക്യം എഴുതുക.

3. എല്ലാ ഉപ ഭോഗ ബണ്ടിലുകളും എഴുതുക.

4. ഉപഭോക്താവിന്റെ ബജറ്റ് രേഖ സമവാക്യം എഴുതുക.

5. വെർട്ടിക്കൽ ഹൊറിസോണ്ടൽ ഇന്റർസെകൾ കാണുക . ബജറ്റ് രേഖ വരയ്ക്കുക.

7. ബജറ്റ് രേഖയുടെ ചെരിവ് കാണുക.

8. ഉപഭോക്താവിന്റെ വരുമാനം 100 ൽനിന്ന് 120 യായി വർധിച്ചാൽ ബജറ്റ് രേഖയിൽ വരുന്ന മാറ്റം ഒരു ഗ്രാഫിൽ കാണിക്കുക.

9. സാധനം 1 ന്റെ വില 10 ൽ നിന്ന് 20 യാകു മ്പോൾ ബജറ്റ് രേഖയിലുള്ള മാറ്റം ഗ്രാഫിലൂടെ വിവരിക്കുക.

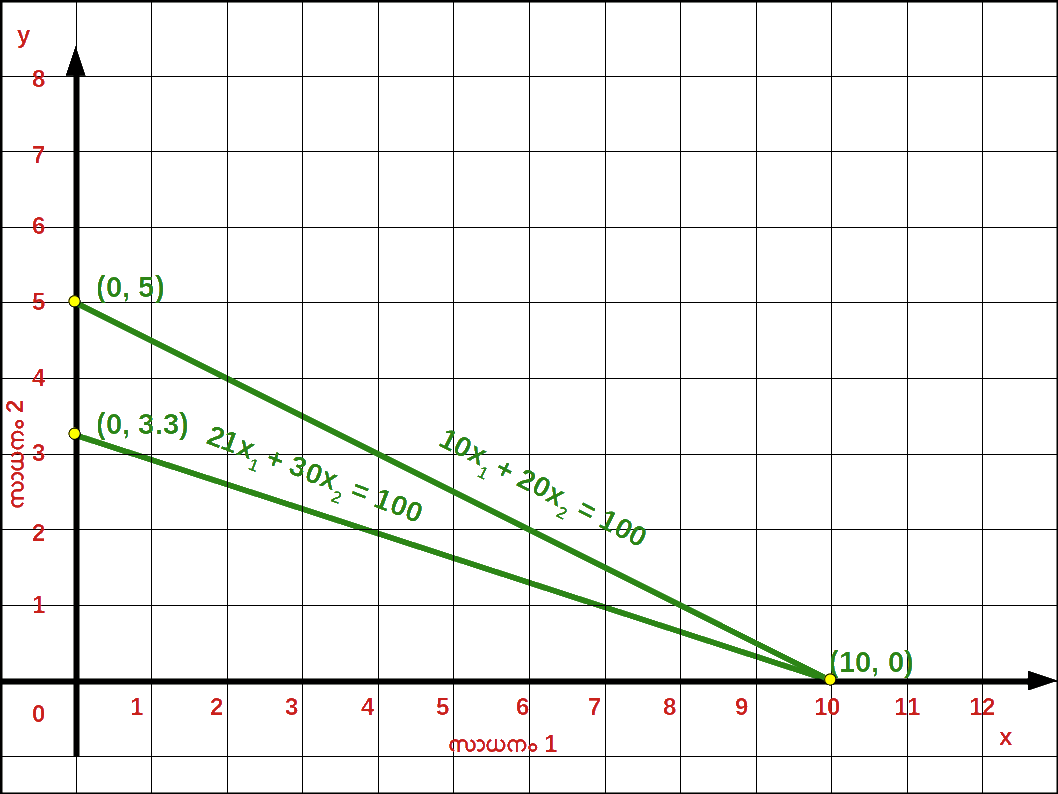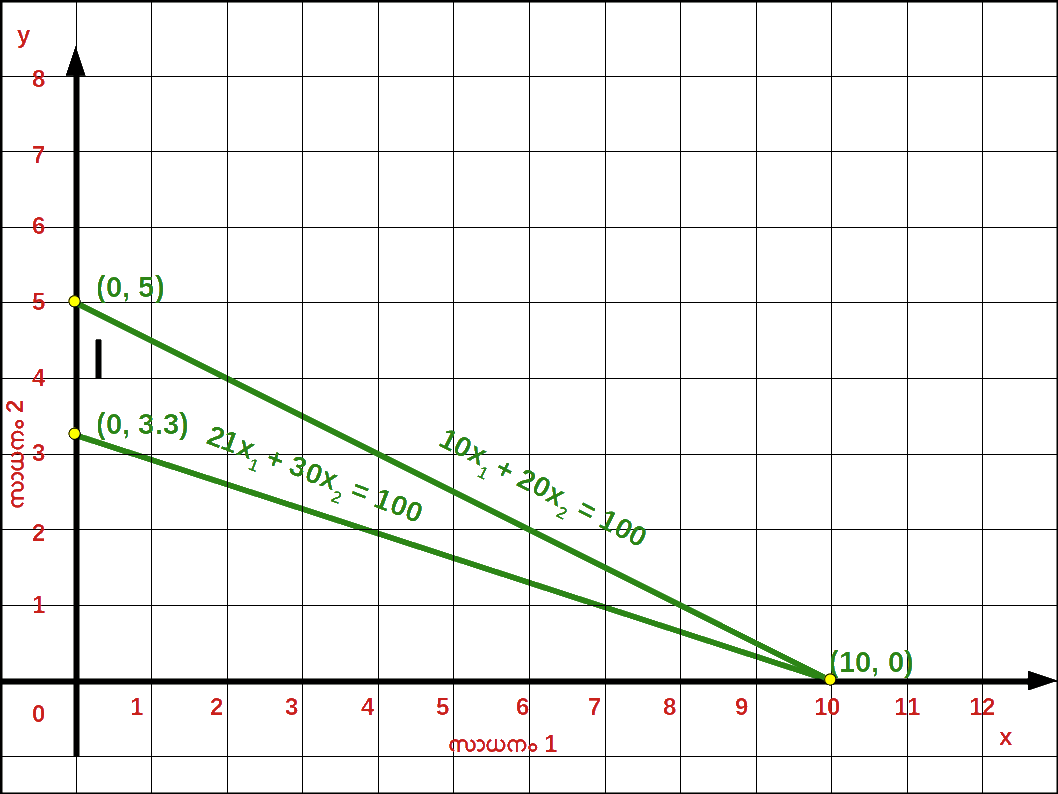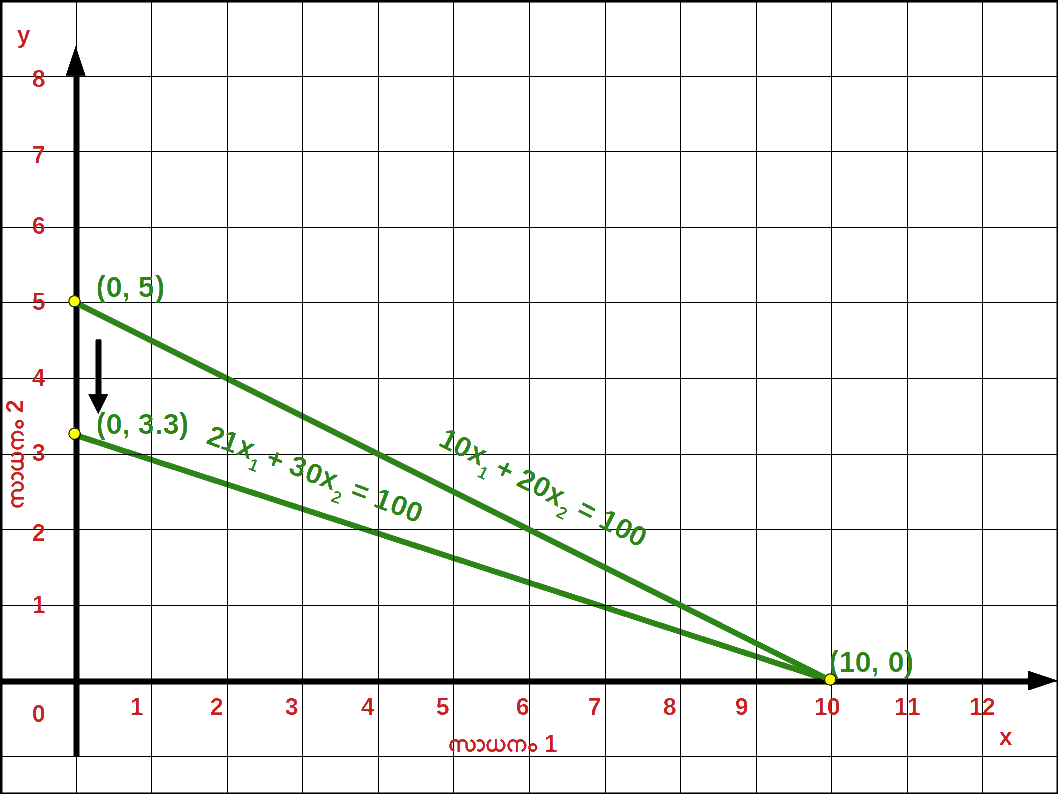
10. സാധനം 2 ന്റെ വില 20 ൽനിന്ന് 30 യായപ്പോൾ ബജറ്റ് രേഖയിലുള്ള മാറ്റം ഗ്രാഫിൽ കാണിക്കുക.

Solution :

1. ഉപഭോക്താവിന്റെ ബജറ്റ് 100 രൂപയാണ്.

2. 10x₁ + 20x₂ ≤ 100

3. ( x₁, x₂ ) എന്ന ക്രമത്തിൽ
( 0 , 0 ) , ( 0 , 1 ) , ( 0 , 2 ) , ( 0 , 3 ) , ( 0 , 4 ) , ( 0 , 5 ) , ( 1 , 0 ) , ( 1 , 1 ) , ( 1 , 2 ) , ( 1 , 3 ) , ( 1 , 4 ) , ( 2 , 0 ) , ( 2 , 1 ) , ( 2 , 2 ) , ( 2 , 3 ) , ( 2 , 4 ) , ( 3 , 0 ) , ( 3 , 1 ) , ( 3 , 2 ) , ( 3 , 3 ) , ( 4 , 0 ) , ( 4 , 1 ) , ( 4 , 2 ) , ( 5 , 0 ) , ( 5 , 1 ) , ( 5 , 2 ) , ( 6 , 0 ) , ( 6 , 1 ) , ( 6 , 2 ) , ( 7,0 ) , ( 7 , 1 ) , ( 8 , 0 ) , ( 8 , 1 ) , ( 9 , 0 ) , ( 10 , 0 )

4. 10x₁ + 20x₂ = 100

5. x₁ = 0 ആയാൽ ,
10 × 0 + 20x₂ = 100
20x₂ = 100
x₂ = $ \mathbf {\frac{100}{20}} $
= 5 വെർട്ടിക്കൽ ഇന്റർസെപ്റ്റ്
x₂ = 0 ആയാൽ ,
10x₁ + 20 × 0 = 100
10x₁ = 100
x₁ = $ \mathbf {\frac{100}{10}} $
= 10 ഹൊറിസോണ്ടൽ ഇന്റർസെപ്റ്റ്

6.

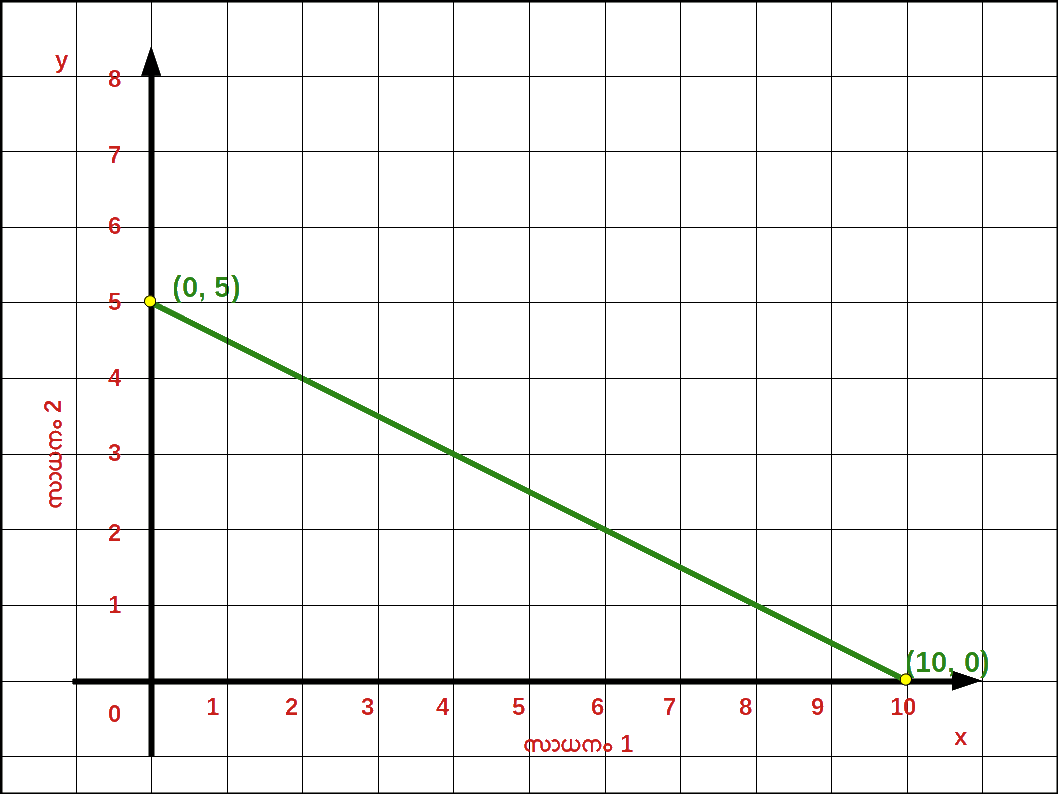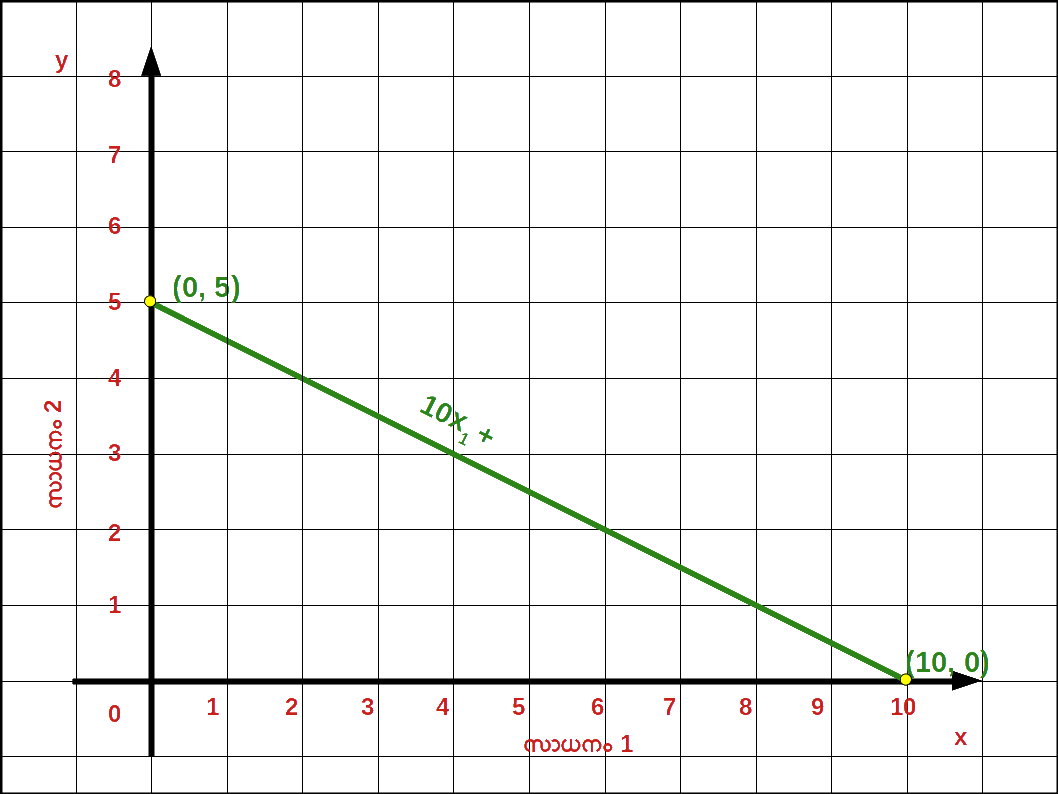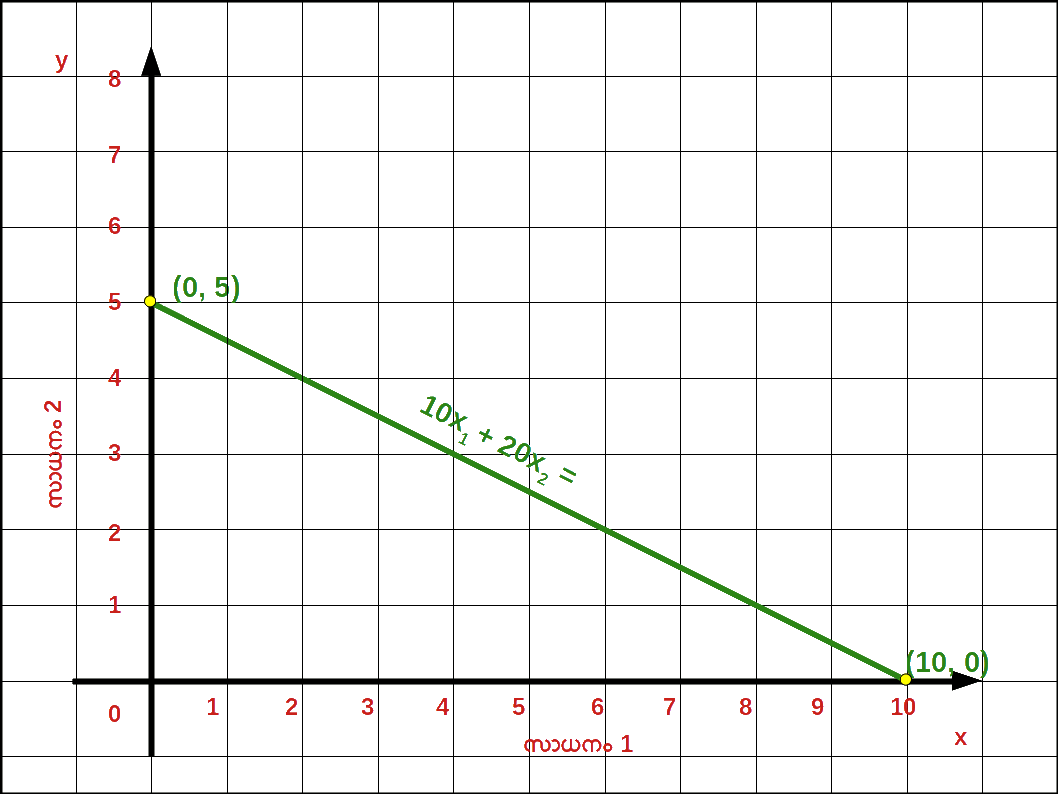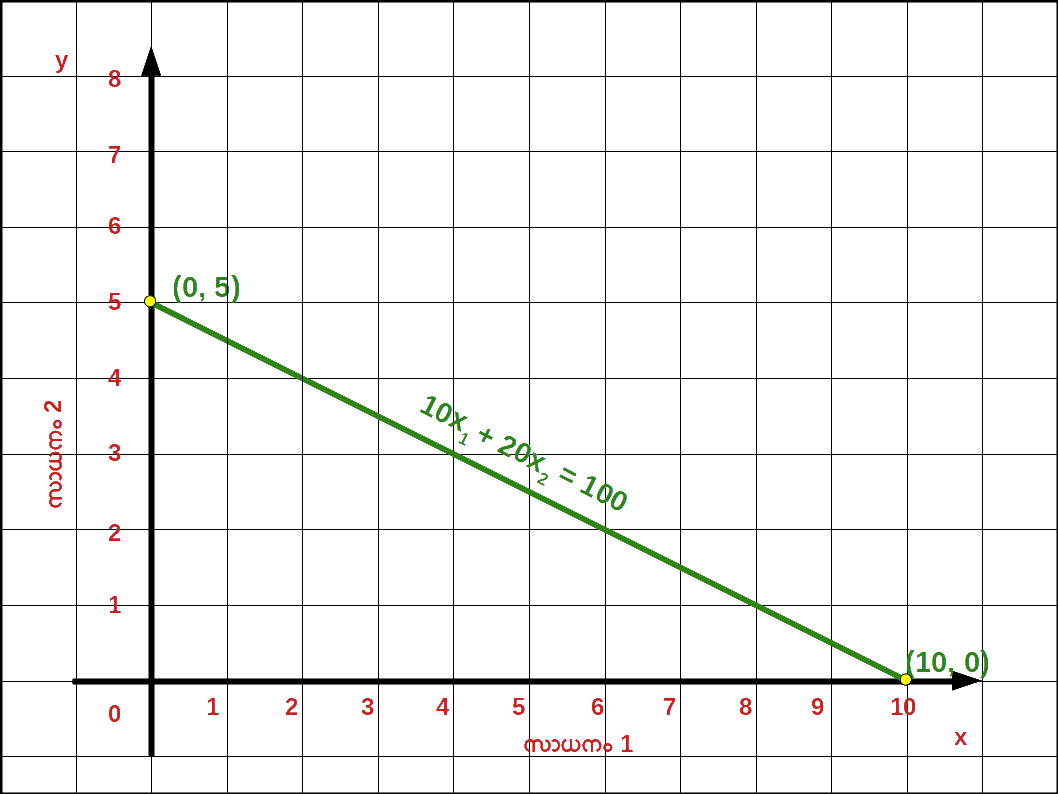
7. ചെരിവ് = $-\, \mathbf {\frac{P_1}{P_2}} $ = $-\, \mathbf {\frac{10}{20}} $ = $ -\,\mathbf {\frac{1}{2}} $ = -5

8. വെർട്ടിക്കൽ ഇന്റർസെപ്റ്റ് 6 ഉം , ഹൊറിസോണ്ടൽ ഇന്റർസെപ്റ്റ് 12 ഉം ആണ്

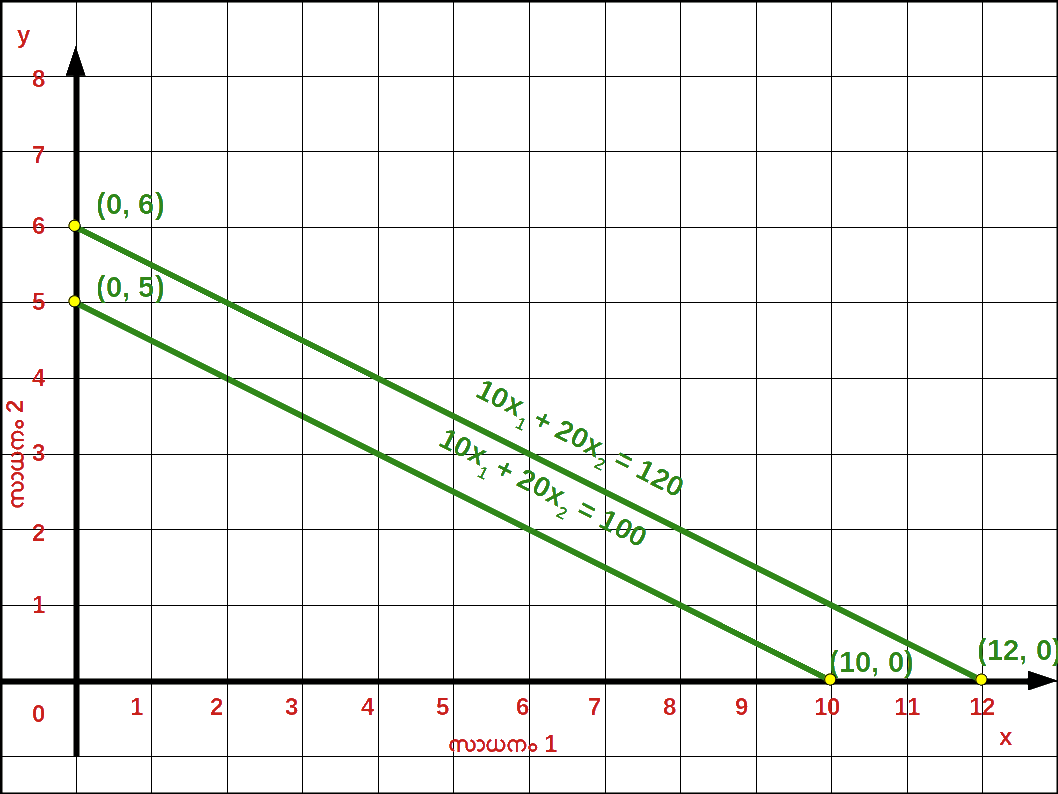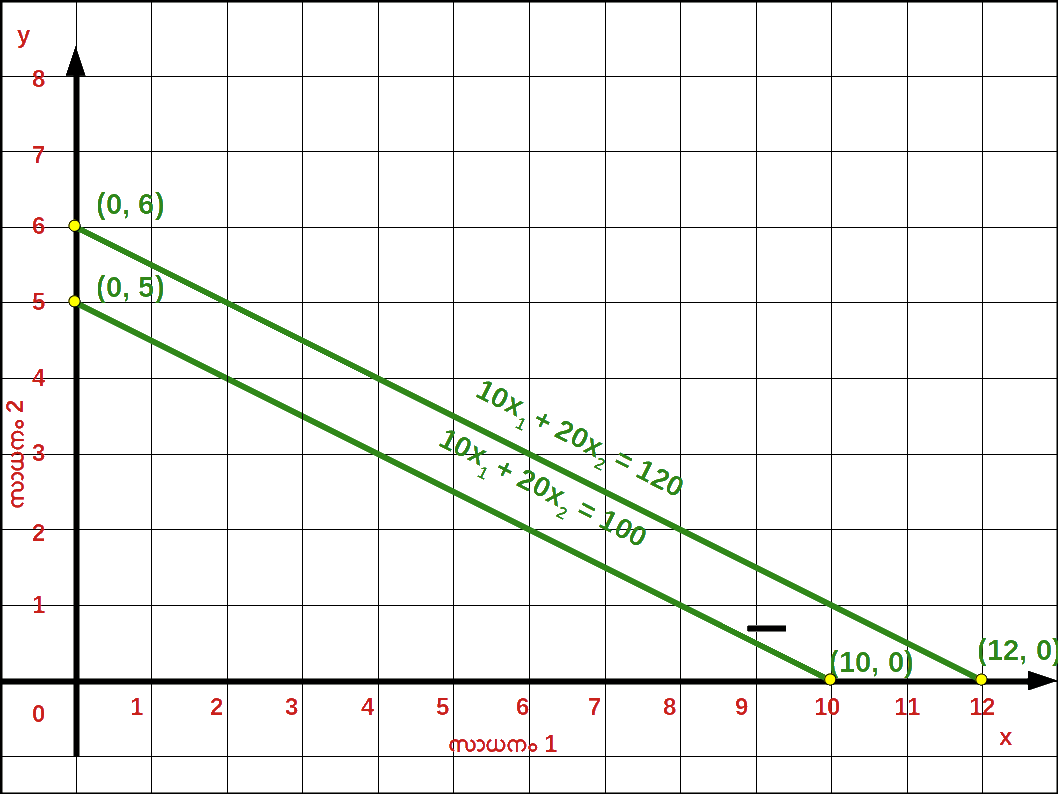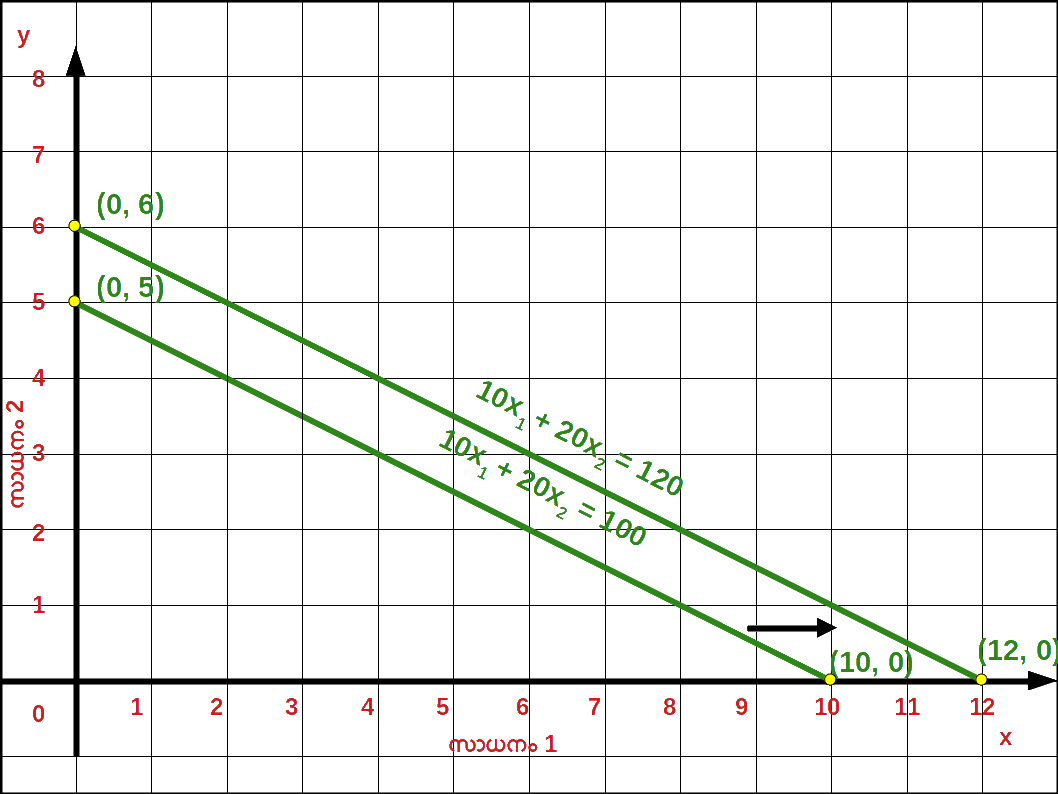വരുമാനം വർധിച്ചതിന്റെ ഫലമായി ബജറ്റ് ലൈൻ വലതുഭാഗത്തേക്കു മാറിയിരിക്കുന്നു

9. സാധനം 1 വില 10 യിൽ നിന്ന് 20 യായി വർധിച്ചപ്പോൾ ഉള്ള ബജറ്റ് രേഖ സമവാക്യം : 20x₁ + 20x₁ = 100 , വെർട്ടിക്കൽ ഇന്റർസെപ്റ്റ് 100/20 = 5 ഉം ഹൊറിസോണ്ടൽ ഇന്റർസെപ്റ്റ് 100/20 = 5 ഉം ആണ്. ബജറ്റ് രേഖയുടെ ചെരിവ് = -1 ആണ്.

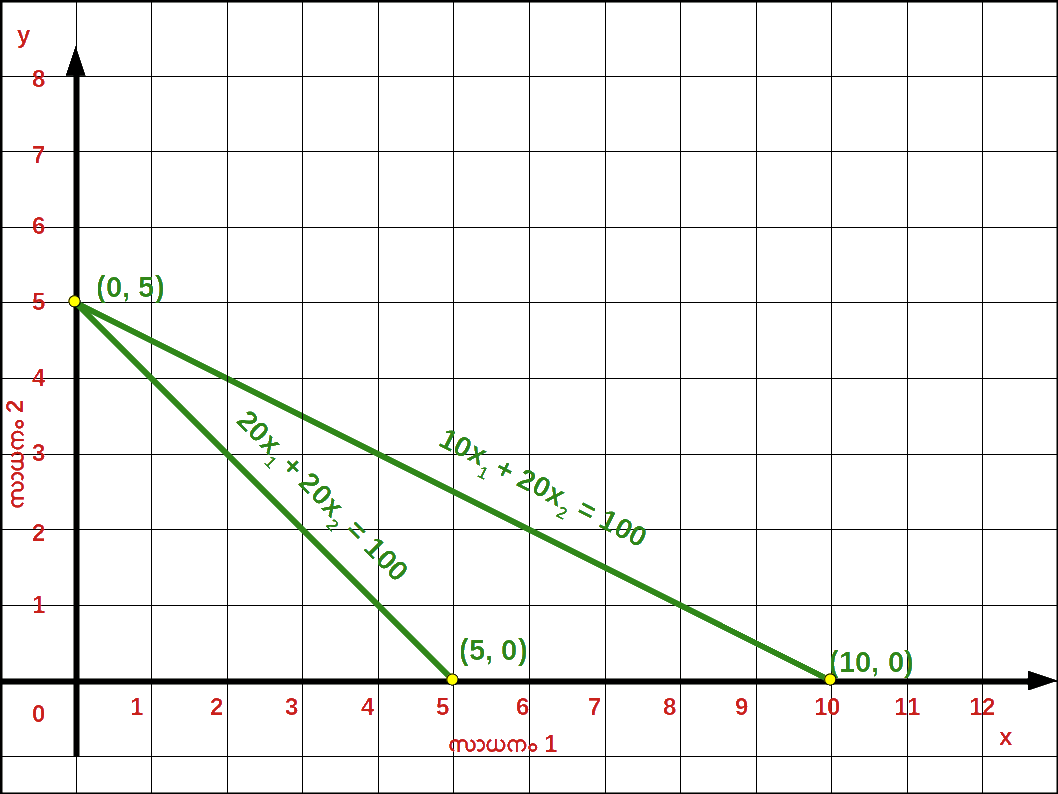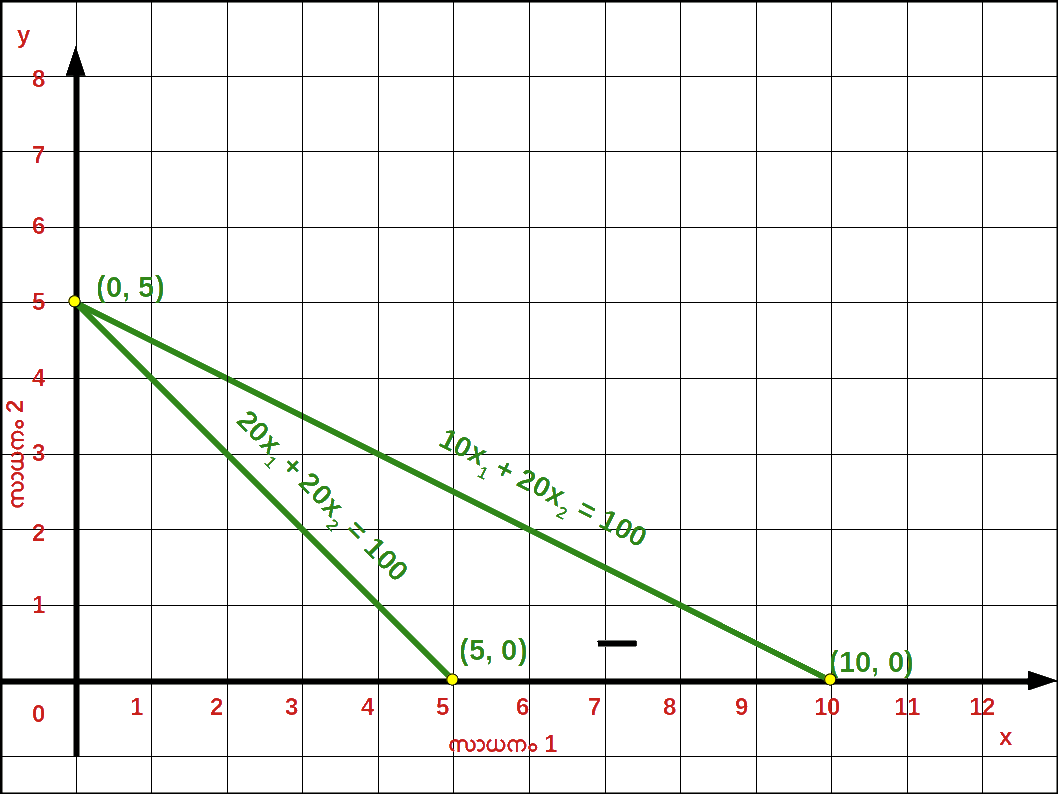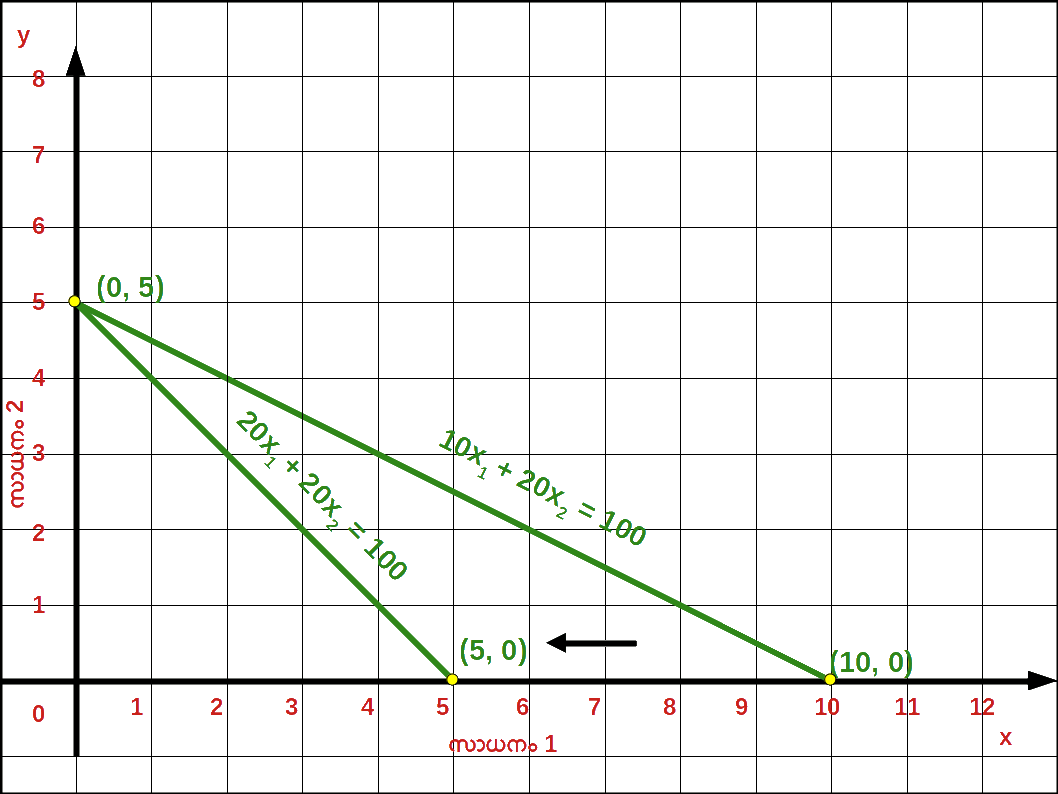
10. സാധനം 2 ന്റെ വില 20 യിൽ നിന്ന് 30 യായപ്പോൾ ബജറ്റ് സമവാക്യം 10x₁ + 30x₂ = 100 , വെർട്ടിക്കൽ ഇന്റർസെപ്റ്റ് 100/30 = 3.33 , ഹൊറിസോണ്ടൽ ഇന്റർസെപ്റ്റ് 100/10 = 10 മാണ്.

ഉപഭോക്താവിന്റെ മുൻഗണനകൾ ( Preferences of the Consumer )
ഉപഭോക്താവ് തനിക്ക് ലഭ്യമായിട്ടുള്ള ബജറ്റ് സെറ്റിൽനിന്ന് ഉപഭോഗ ബണ്ടിലുകൾ തെരഞ്ഞെടുക്കുന്നത് അയാളുടെ അഭിരുചികളും മുൻഗണനാ ക്രമവും അനുസരിച്ചായിരിക്കും. ഉപഭോക്താവ് ബണ്ടിലുകൾ താരതമ്യപ്പെടുത്തുന്നു. ഉപഭോക്താവിന് ഏതെങ്കിലും ഒരു ബണ്ടിലിനോട് കൂടുതൽ താല്പര്യ മുണ്ടാകുകയോ അല്ലെങ്കിൽ അവയോട് നിസംഗത ( indifference ) പുലർത്തുകയോ ചെയ്യാം. ഉപഭോക്താവിന് തന്റെ താല്പര്യമനുസരിച്ച് ബണ്ടിലുകളെ റാങ്ക് ചെയ്യാവുന്നതാണ്.
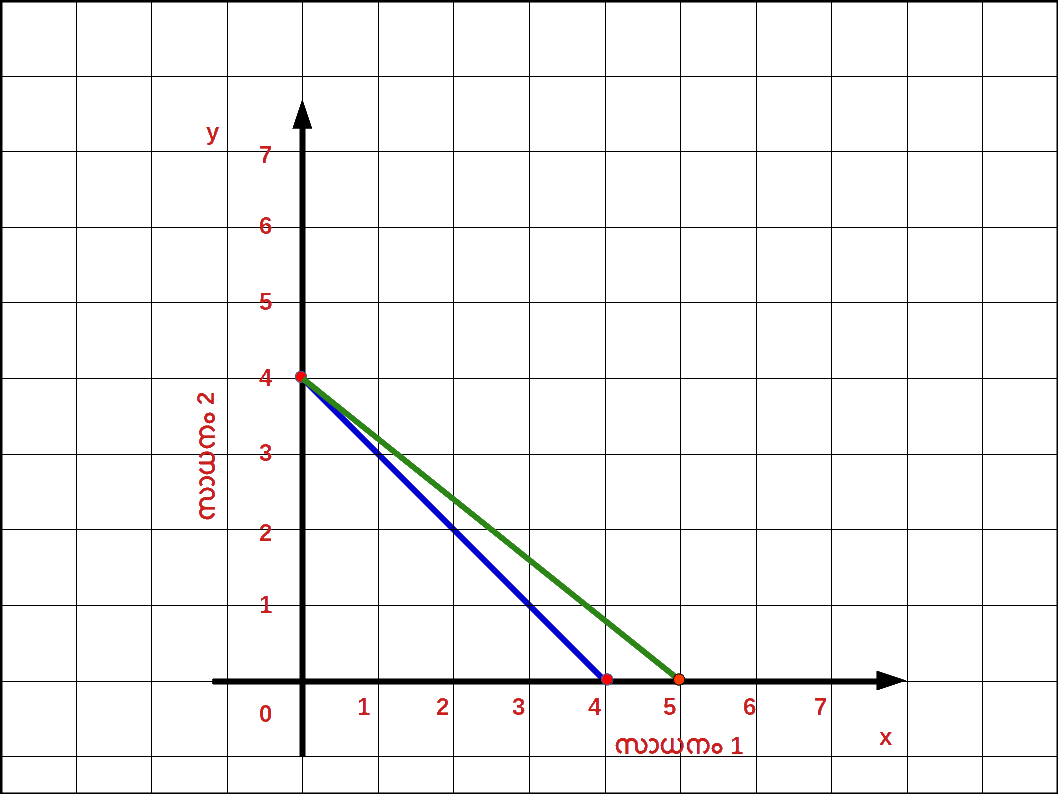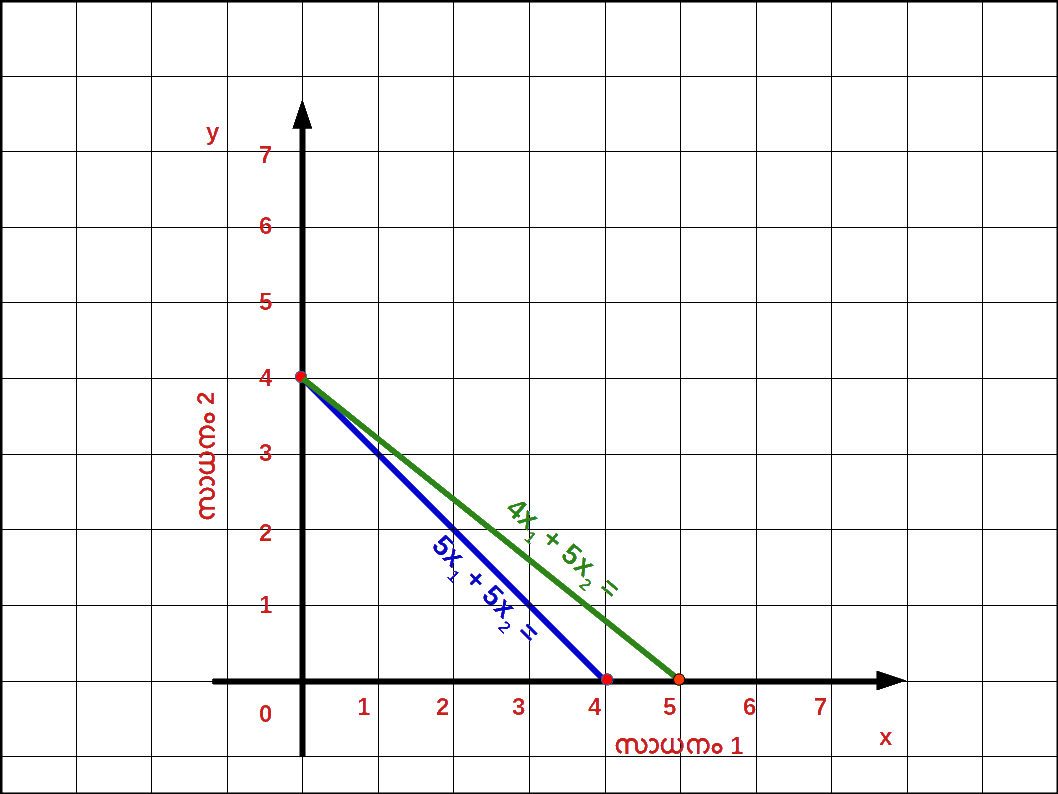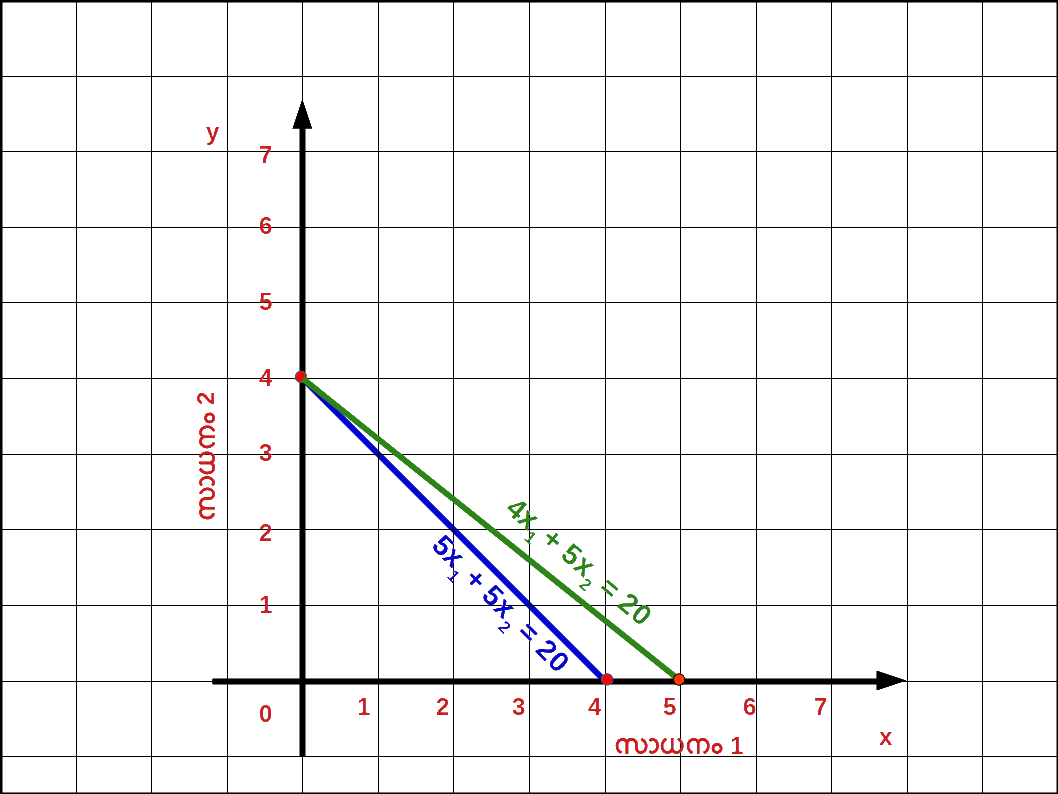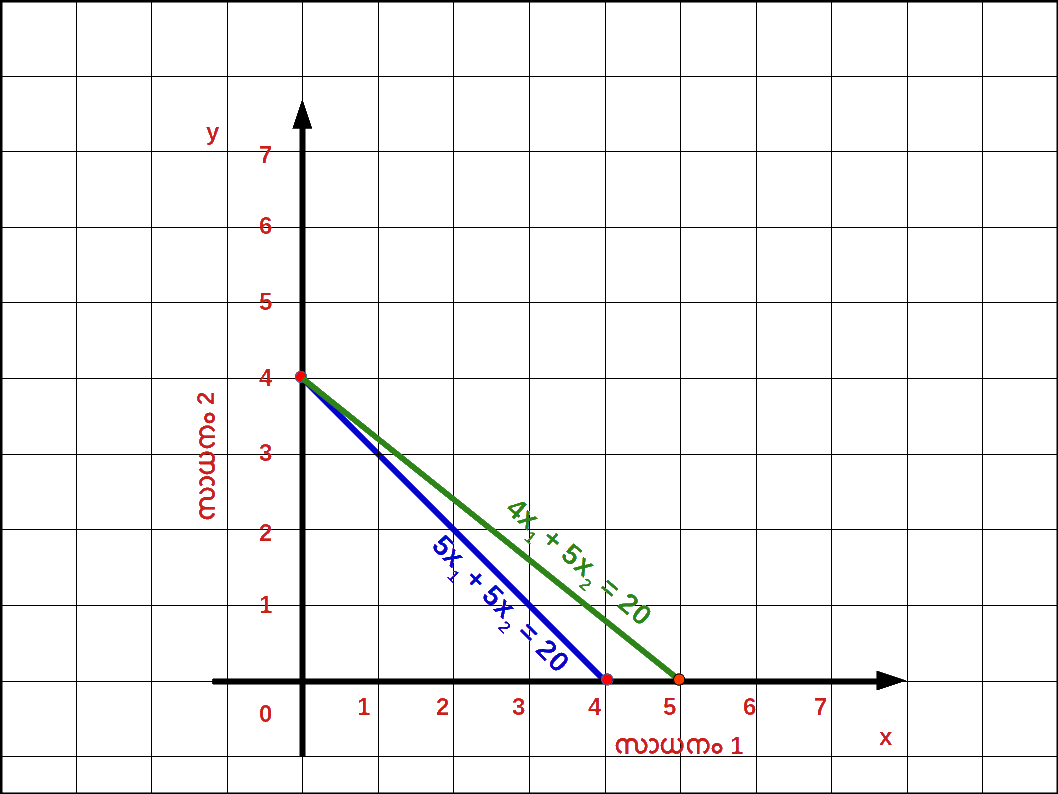
5x₁ + 5x₂ ≤ 20 എന്ന ബജറ്റ് സെറ്റ് പ്രകാരമുള്ള ഉപഭോഗ ബണ്ടിലുകളെ താഴെ പട്ടികയിൽ കൊടുത്തതുപ്രകാരം മുൻഗണനാക്രമത്തിൽ റാങ്ക് ചെയ്തിരിക്കുന്നു.

Table 2.2

ബണ്ടിലുകൾ റാങ്കിങ്

(2, 2) I

(1, 3), (3, 1) II

(1, 2), (2, 1) III

(1, 1) IV

(0, 1), (0, 2), (0, 3), (0, 4), (1, 0), (2, 0), (3, 0), (4, 0) V

ഏറ്റവും ആഭിമുഖ്യമുള്ള ബണ്ടിൽ ( 2, 2 ) ആണ്. (1, 3), (3 , 1) എന്നീ ബണ്ടിലുകൾ ഉപഭോക്താവിന് നിസംഗതാ മനോഭാവമാണ്. ഈ ബണ്ടിലുകൾ ഒരേ തോതിലുള്ള സംതൃപ്തിയാണ് നല്കുന്നത്. അതുപോലെ (1, 2), (2, 1) എന്നീ ബണ്ടിലുകൾ ഒരേ സംതൃപ്തിയാണ് നല്കുന്നത് മുൻഗണന അല്ലെങ്കിൽ റാങ്കിങ് വ്യക്തിഭേദമനുസരിച്ചു മാറിക്കൊണ്ടിരിക്കും.

മൊണോടോണിക് പ്രിഫറൻസ് ( Monotonic Preferences )
കുറഞ്ഞ അളവുള്ള ബണ്ടിലിനെക്കാൾ കൂടുതൽ അളവുള്ള ബണ്ടിലിനോടുള്ള ഉപഭോക്താവിന്റെ താല്പര്യത്തെ മൊണോടോണിക് പ്രിഫറൻസ് എന്നു പറയുന്നു. ഏതെങ്കിലും രണ്ട് ബണ്ടിലുകളിൽ ഏതു ബണ്ടിലിനാണോ മറ്റേ ബണ്ടിലുമായി താരതമ്യം ചെയ്യുമ്പോൾ ഏതെങ്കിലും ഒരു സാധനത്തിന്റെ അളവ് ഒരു മാത്രയെങ്കിലും കൂടുതൽ ഉള്ളതും മറ്റേ സാധനത്തിന്റെ അളവിൽ ഒട്ടും കുറയാതെയിരിക്കുകയും ചെയ്യുന്നത്, ആ ബണ്ടിലിന് ഉപഭോക്താവ് മുൻഗണന നല്കുന്നതിന് മൊണോടോണിക് പ്രിഫറൻസ് എന്നു പറയുന്നു. ( x₁, x₂ ), ( y₁, y₂ ) എന്നീ ബണ്ടിലുകൾ തമ്മിൽ താരതമ്യം ചെയ്യുമ്പോൾ x₁ന്റെ അളവ് y₁ നേക്കാൾ കൂടുതലായിരിക്കുകയും x₂ ന്റെ അളവ് x₂ നേക്കാൾ കുറയാതെയിരിക്കുകയും ചെയ്താൽ ഉപഭോക്താവ് ( x₁, x₂ ) എന്ന ബണ്ടിൽ തെരഞ്ഞെടുക്കുന്നു. അപ്പോൾ ഉപഭോക്താവിന്റെ മുൻഗണന മൊണോട്ടോണിക്കാണെന്ന് പറയാം.
EXAMPLE 2.10 പട്ടിക 2.2 ൽ ( 2 , 1 ) എന്ന ബണ്ടിലിനെക്കാൾ മുൻഗണന ( 2 , 2 ) എന്ന ബണ്ടിലിന് നല്കുന്നു. കാരണം ( 2 , 2 ) എന്ന ബണ്ടിലിൽ രണ്ടാമത്തെ സാധനത്തിന്റെ 1 യൂണിറ്റ് ( 2 , 1 ) എന്ന ബണ്ടിലിനെ അപേക്ഷിച്ച് കൂടുതലാണ്. ( 2 , 1 ) എന്ന ബണ്ടിലാണ് ഉപഭോക്താവ് തെരഞ്ഞെടുക്കുന്നതെങ്കിൽ അയാളുടെ മുൻഗണന മൊണോട്ടോണിക്കല്ല.

രണ്ട് സാധനങ്ങൾക്കിടയിലെ പ്രതിസ്ഥാപനം ( Substitution between two goods )
ഉപഭോക്താവിന് രണ്ടു ബണ്ടിലുകളിൽ നിന്നും ഒരേ തോതിലുള്ള സംതൃപ്തിയാണ് ലഭിക്കുന്നതെങ്കിൽ അയാൾക്ക് ഒരു ബണ്ടിലിനുപകരം മറ്റൊരു ബണ്ടിൽ സ്വീകരിക്കുന്നതിൽ വിരോധമില്ല. തുല്യ സംതൃപ്തി നല്കുന്ന രണ്ടോ രണ്ടിൽ കൂടുതലോ ബണ്ടിലുകൾ തമ്മിൽ പരസ്പരം മാറ്റുന്നതിനെയാണ് രണ്ട് സാധനങ്ങൾക്കിടയിലെ പ്രതിസ്ഥാപനം എന്നു പറയുന്നത്. മറ്റൊരു വിധത്തിൽ പറഞ്ഞാൽ , ഒരു സാധനത്തിന്റെ ഏതാനും മാത്രകൾക്ക് പകരം മറ്റൊരു സാധനത്തിന്റെ കൂടുതൽ ഉപയോഗിക്കുന്നതിനെയാണ് പ്രതിസ്ഥാപനം എന്ന് പറയുന്നത്.
EXAMPLE 2.11 പട്ടിക 2.2 ൽ ( 1 , 3 ) , ( 3, 1 ) എന്നീ ബണ്ടിലുകൾ ഉപഭോക്താവിന് തുല്യ സംതൃപ്തി നല്കുന്ന നിസംഗതാ ബണ്ടിലുകളാണ്. ( 1 , 3 ) എന്ന ബണ്ടിലിനുപകരം ( 3, 1 ) എന്ന ബണ്ടിൽ സ്വീകരിക്കുന്നതിനെ പ്രതിസ്ഥാനം എന്നു പറയുന്നു. ഈ രണ്ടു ബണ്ടിലിനും തുല്യ റാങ്കാണ്. ( x₁, x₂ ) , ( x₁ + Δx₁ , x₂ + Δx₂ ) എന്നീ ബണ്ടിലുകൾ നിസംഗത ബണ്ടിലുകളാകണമെങ്കിൽ Δx₁ > 0 യാകുമ്പോൾ ( Δx₁ = സാധനം 1 ലുള്ള മാറ്റം ) Δx₂ < 0 ആയിരിക്കണം. ( Δx₂ = സാധനം 2 ലുള്ള മാറ്റം ). അതുപോലെ Δx₁ < 0 ആകുമ്പോൾ Δx₁ > 0 ആയിരിക്കണം. അതുകൊണ്ട് ഉപഭോക്താവിന് ഒരു സാധനത്തിന്റെ സ്ഥാനത്ത് മറ്റൊരു സാധനം പ്രതിസ്ഥാപനം നടത്തി ( x₁, x₂ ) എന്ന ബണ്ടിലിൽനിന്നും , ( x₁ + Δx₁ , x₂ + Δx₂ ), എന്ന ബണ്ടിലിലേക്ക് മാറാൻ കഴിയും.

പ്രതിസ്ഥാപന നിരക്ക് ( Rate of Substitutlon )
നിസംഗമായ രണ്ട് ഉപഭോഗ ബണ്ടിലുകളിൽ ഒരു സാധനത്തിന്റെ കൂടുതൽ യൂണിറ്റ് ലഭിക്കാൻ വേണ്ടി ത്യജിക്കുന്ന അഥവാ ഉപേക്ഷിക്കുന്ന മറ്റേ സാധനത്തിന്റെ അളവിനെയാണ് രണ്ട് സാധനങ്ങൾ തമ്മിലുള്ള പ്രതിസ്ഥാപന നിരക്ക് എന്നു പറയുന്നത്.
അതായത് , ത്യജിക്കപ്പെടുന്ന സാധനത്തിന്റെ അളവിലെ മാറ്റവും നേടുന്ന സാധനത്തിന്റെ അളവിലെ മാറ്റവും തമ്മിലുള്ള അനുപാതത്തിന്റെ കേവല മൂല്യം ( absolute value ) പ്രതിസ്ഥാപന നിരക്ക് എന്ന് നിർവചിക്കാം. ഒന്നാമത്തെ സാധനത്തിന്റെ അളവിലുള്ള മാറ്റം Δx₁ ഉം രണ്ടാമത്തെ സാധനത്തിന്റെ അളവിലുള്ള മാറ്റം Δx₂ വുമാണങ്കിൽ , ഒന്നാമത്തെ സാധനത്തിനുവേണ്ടി രണ്ടാമത്തെ സാധനത്തിന്റെ പ്രതിസ്ഥാപന നിരക്കിനെ $ \mathbf {\frac{Δx_2}{Δx_1}} $ എന്ന കേവല മൂല്യത്താൽ പ്രതിനിധീകരിക്കുന്നു.
EXAMPLE 2.12 : ( 2 , 2 ) , ( 1 , 3 ) എന്നീ ബണ്ടിലുകൾ പരിഗണിക്കുക. Δx₂ = / 2 – 1 / = 1 , Δx₂ = / 2 – 3 / = 1 ; ആയതുകൊണ്ട് $ \mathbf {\frac{Δx_2}{Δx_1}} $ = $ \mathbf {\frac{1}{1}} $ = 1. പ്രതിസ്ഥാപന നിരക്ക് 1. അതായത് , സാധനം 1 ന്റെ യൂണിറ്റ് കിട്ടാൻ വേണ്ടി സാധനം 2 ന്റെ യൂണിറ്റ് ത്യജിക്കുന്നു. അപ്പോൾ അവ തമ്മിലുള്ള അനുപാതം 1 : 1 ആണ്.

കുറഞ്ഞുകൊണ്ടിരിക്കുന്ന പ്രതിസ്ഥാപന നിരക്ക് ( Diminishing Rate of Substitution )
ഉപഭോക്താവിന് സാധനം 1 ന്റെ കൂടുതൽ അളവ് വേണമെങ്കിൽ സാധനം 2 ന്റെ അളവ് കുറച്ചു കൊണ്ട് കഴിയൂ. സാധനം 1 ന്റെ കൂടുതൽ കൂടുതൽ ലഭിക്കുന്നതിനു വേണ്ടി സാധനം 2 ന്റെ ത്യജിക്കുന്ന അളവ് കുറഞ്ഞ് കുറഞ്ഞ് വരുന്നതിനെയാണ് കുറഞ്ഞുകൊണ്ടിരിക്കുന്ന പ്രതിസ്ഥാപന നിരക്ക് എന്നു പറയുന്നത്. അതായത് , പ്രതിസ്ഥാപന നിരക്കിന്റെ കേവലമൂല്യം കുറഞ്ഞുകൊണ്ടിരിക്കും. ഇതിനെ കോൺവെക്സ് പ്രിഫറൻസ് എന്നു പറയുന്നു.

സീമാന്ത പ്രതിസ്ഥാപന നിരക്ക് ( Marginal Rate of Substitution- MRS )
ഒരു സാധനത്തിന്റെ ഒരു അധിക മാത്ര ലഭിക്കുന്നതിനുവേണ്ടി മറ്റേ സാധനത്തിന്റെ ത്യജിക്കപ്പെട്ട അളവിനെയാണ് സീമാന്ത പ്രതിസ്ഥാപന നിരക്ക് ( MRS ) എന്നു പറയുന്നത് . ഒരു മാത്ര ലഭിക്കാൻ വേണ്ടി ഉപേക്ഷിച്ച സാധനത്തിന്റെ അളവാണിത്. ഒന്നാമത്തെ സാധനത്തിന്റെ ഒരു അധിക മാത്രം നേടുന്നതിനുവേണ്ടി രണ്ടാമത്തെ സാധനത്തിന്റെ ഉപേക്ഷിക്കപ്പെട്ട അളവിനെ ഒന്നാമത്തെ സാധനത്തിനുവേണ്ടിയുള്ള രണ്ടാമത്തെ സാധനത്തിന്റെ സീമാന്ത പ്രതിസ്ഥാപന നിരക്ക് എന്ന് പറയുന്നു. ഗണിത രൂപത്തിൽ:

$ \mathbf {MRS_{xy} \,= \,\frac{Δx_2}{Δx_1}} $ എന്നത് ഒന്നാമത്തെ സാധനത്തിനുവേണ്ടിയുള്ള രണ്ടാമത്തെ സാധനത്തിന്റെ സീമാന്ത പ്രതിസ്ഥാപന നിരക്കാണ്.

താഴെ കൊടുത്തിരിക്കുന്ന പട്ടിക നോക്കുക.

Table 2.3

മിശ്രണം (സാധനം 2x₁) സാധനം 1 (x₂) $ \mathbf {MRS_{x_{1}x_{2}} \,= \,\frac{Δx_2}{Δx_1}} $

a 11 1 –

b 7 2 1:4

c 4 3 1:3

d 2 4 1:2

e 1 5 1:1

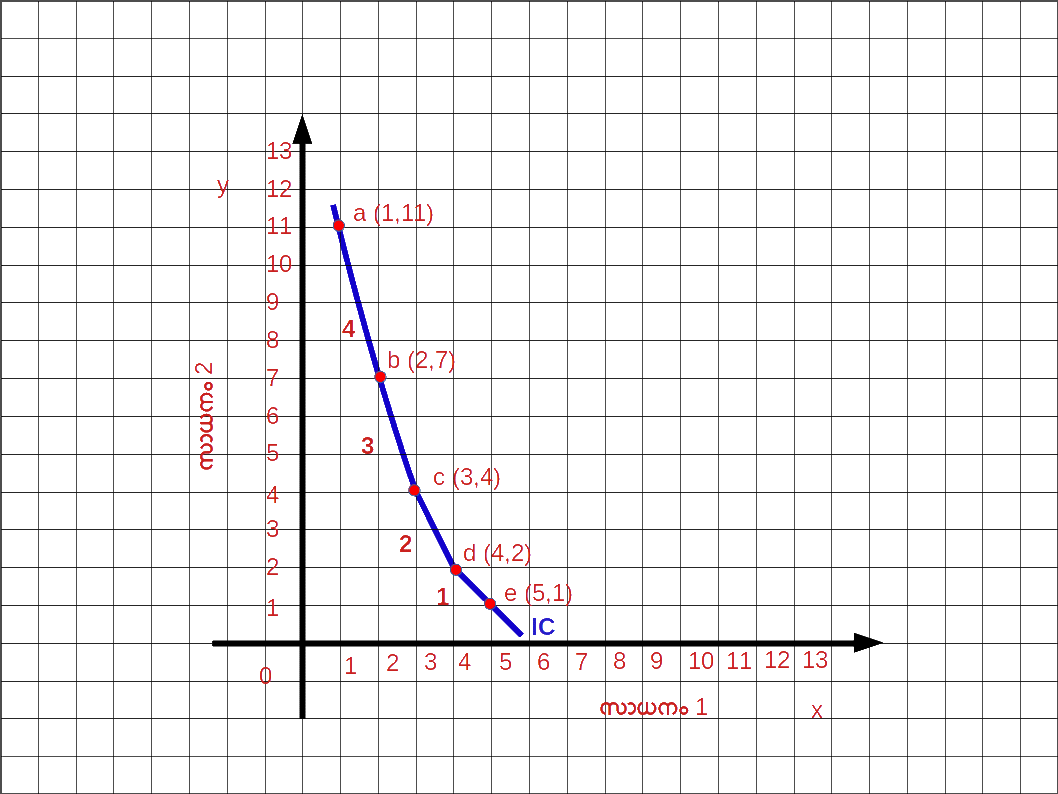
( 1 , 11 ) , ( 2 , 7 ) , ( 3 , 4 ) , ( 4 , 2 ) , ( 5 , 1 ) എന്നിവ നിസ്സംഗമായ ബണ്ടിലുകളാണ്. ഈ ബണ്ടിലുകൾ ഉപഭോക്താവിന് ഒരേ തലത്തിലുള്ള സംതൃപ്തി നൽകുന്നു. സാധനം 1 ന്റെ ഒരു യൂണിറ്റ് കൂടുതൽ വാങ്ങാൻ വേണ്ടി വേണ്ടെന്ന് വയ്ക്കുന്ന സാധനം 2 ന്റെ അളവ് കുറയുന്നു. ഒന്നാമത്തെ ബണ്ടിലിൽ ( 1 , 11 ) നിന്ന് അഞ്ചാമത്തെ ബണ്ടിലിലേക്ക് ( 5 , 1 ) മാറുന്ന തിനനുസരിച്ച് MRS_x1x2 . 4 , 3 , 2 , 1 എന്നിവയാണ്.
നിസംഗതാവക്രം അഥവാ ഉദാസീനതാവക്രം ( Indifference Curve )
തുല്യ സംതൃപ്തി നല്കുന്ന രണ്ട് സാധനങ്ങളുടെ വിവിധ സംയോഗങ്ങൾ ചേർന്ന ബിന്ദു യോജിപ്പിച്ച് വരച്ച് ലഭിക്കുന്ന വക്രത്തെ നിസംഗതാവക്രം എന്നു പറയുന്നു. ഒരേ സംതൃപ്തി ലഭിക്കുന്ന ഉപഭോഗ ബണ്ടിലുകൾ ചേർത്ത് വരയ്ക്കുന്ന രേഖാ ചിത്രമാണ് നിസംഗതാവകം ഡയഗ്രം 2.16 ൽ നിസംഗതാവകം വരച്ചിരിക്കുന്നു.

Diagram 2.16

Diagram 2.17

A , B എന്നിവ നിസംഗതാവക്രത്തിലെ രണ്ട് ബിന്ദുക്കളാണ്. ( x₁, x₂ ) , ( y₁, y₂ ) എന്നീ ഉപബണ്ടിലുകൾ ഉപഭോക്താവിന് തുല്യ സംതൃപ്തിനല്കുന്നു. ഉദാസീനതാവക്രത്തിനു പുറത്തുള്ള ഏതൊരു ബണ്ടിലും , ഉദാഹരണമായി എന്ന ബിന്ദുവിലെ ബണ്ടിലിനെ നിസംഗതാവക്രത്തിന്മേലുള്ള ബണ്ടിലിനെക്കാളും താല്പര്യപ്പെടുന്നു. എന്നാൽ ഉദാസീനതാവക്രത്തിനു താഴെയുള്ള ഏതൊരു ബണ്ടിലും ഉദാഹരണമായി നിസംഗതാ വക്രത്തിന്മേലുള്ള ഒരു ബണ്ടിലിനെക്കാളും താല്പര്യം കുറഞ്ഞതായിരിക്കും. പട്ടിക 2.3 – ൽ കൊടുത്ത വിവരങ്ങൾ പ്രകാരം നിസംഗതാവക്രം ഗ്രാഫ് 2.17 ൽ വരച്ചിരിക്കുന്നു.
ഗ്രാഫിൽ a , b , c , d , e എന്നിവ IC എന്ന നിസംഗതാവക്രത്തിലെ ഏതാനും ചില ബണ്ടിലുകളാണ്. ഈ ബണ്ടിലുകളെല്ലാം തുല്യ സംതൃപ്തി നല്കുന്നു. ഈ ബണ്ടിലുകളുടെ ( ബിന്ദുക്കളുടെ ) കൂട്ടമാണ് നിസംഗതാവക്രം. ഇവിടെ ( 1 , 11 ) എന്ന ഉപഭോഗ ബണ്ടിലിൽ നിന്ന് ( 2 , 7 ) എന്ന ബണ്ടിലിലേക്ക് മാറുമ്പോൾ സാധനം 1 ന്റെ ഒരു മാത്ര കൂടുകയും സാധനം 2 ന്റെ 4 മാത്രകൾ ഉപേക്ഷിക്കുകയും ചെയ്യുന്നു. അപ്പോൾ സീമാന്ത പ്രതിസ്ഥാപന നിരക്ക് 4 ആണ്. a എന്ന ബണ്ടിലിൽ നിന്ന് താഴോട്ട് b , c , d എന്നിവയിലൂടെ e എന്ന ബണ്ടിലിൽ എത്തുമ്പോൾ MRS_x1x2 കുറഞ്ഞ് കുറഞ്ഞ് വരുന്നതായിക്കാണാം.

പ്രതിസ്ഥാപന നിരക്കും നിസംഗതാവക്രത്തിന്റെ ചെരിവും
പ്രതിസ്ഥാപന നിരക്ക് അഥവാ സീമാന്ത പ്രതിസ്ഥാപന നിരക്കാണ് നിസംഗതാവക്രത്തിന്റെ ചെരിവ്. ( x₁, x₂ ) , ( x₁ + Δx₁ , x₂ + Δx₂ ) എന്നിവ നിസംഗതാവളത്തിലെ രണ്ടു ബിന്ദുക്കളാണെന്ന് കരുതുക. ( x₁, x₂ ) എന്ന ബിന്ദുവിൽ നിന്നും ( x₁ + Δx₁ , x₂ + Δx₂ ) എന്ന നിസംഗതാവക്രത്തിലുള്ള മറ്റൊരു ബിന്ദുവിലേക്ക് ഉപഭോക്താവ് മാറുമ്പോൾ , ഈ രണ്ടു ബിന്ദുക്കൾ യോജിപ്പിച്ചുകൊണ്ട് വരയ്ക്കുന്ന നേർരേഖയുടെ ചെരിവാണ് നിസംഗതാ വക്രത്തിന്റെ ചെരിവ്. നിസംഗതാവക്രത്തിന്റെ ചെരിവ് എന്നത് പ്രതിസ്ഥാപന നിരക്കിന് തുല്യമാണ്. ഒരു നിസംഗതാവക്രത്തിൽ ഒന്നാമത്തെ സാധനത്തിന്റെ അളവ് ഒരു യൂണിറ്റ് കൂടുമ്പോൾ രണ്ടാമത്തെ സാധനത്തിന്റെ അളവ് കുറയുന്നു. ത്യജിക്കുന്ന സാധനത്തിന്റെ അളവും നേടുന്ന സാധനത്തിന്റെ അളവും തമ്മിലുള്ള അനുപാതത്തിന്റെ കേവലമൂല്യമാണ് പ്രതിസ്ഥാപന നിരക്ക് അഥവാ സീമാന്ത പ്രതിസ്ഥാപന നിരക്ക്. ഇതു തന്നെയാണ് നിസംഗതാവക്രത്തിന്റെ ചെരിവും ഇത് ഡയഗ്രം 2.18 ൽ കൊടുത്തിരിക്കുന്നു.

Diagram 2.18

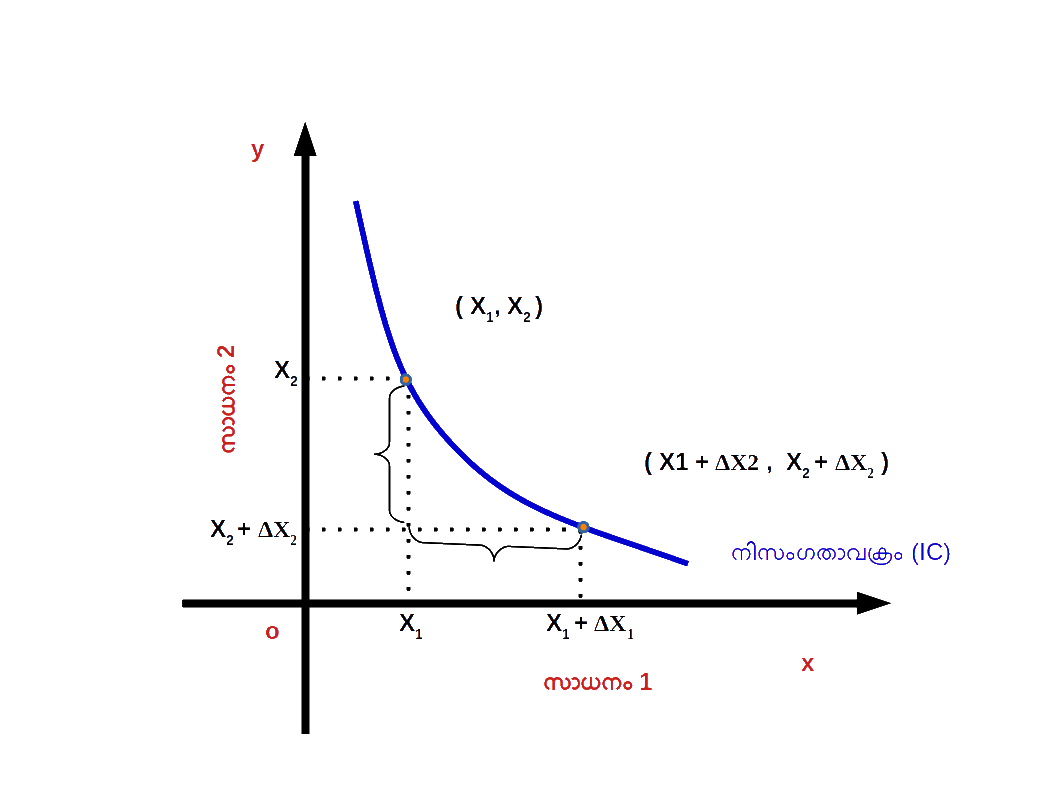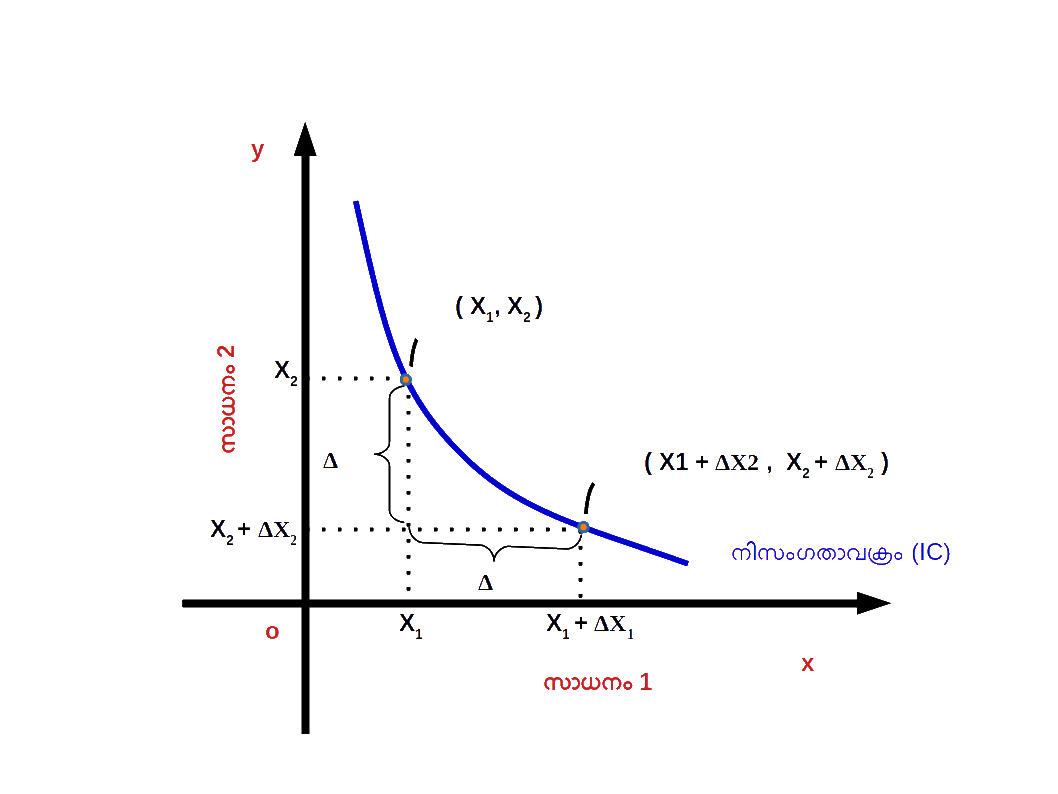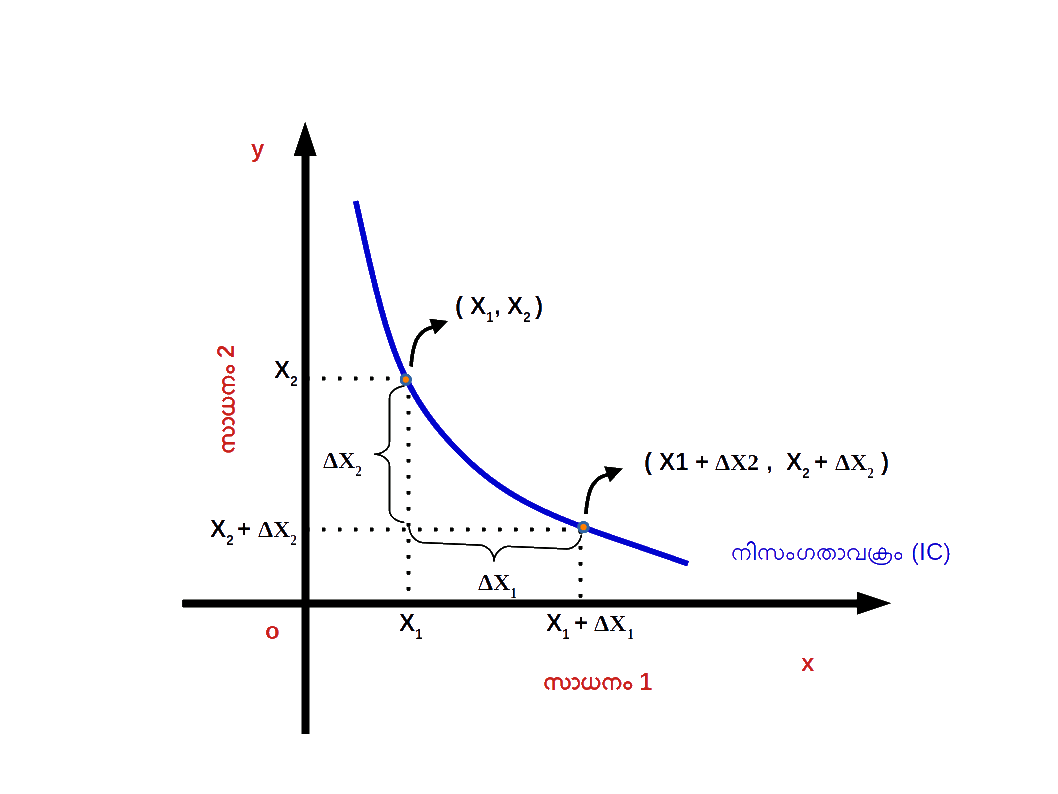
ഉദാസീനതാവക്രത്തിന്റെ ചെരിവ് = പ്രതിസ്ഥാപന നിരക്ക് = സീമാന്ത പ്രതിസ്ഥാപന നിരക്ക് = $ \mathbf {MRS_{xy} \,= \,\frac{Δx_2}{Δx_1}} $

ഉദാസീനതാവക്രം മുകളിൽനിന്ന് താഴേക്ക് ചെരിഞ്ഞിരിക്കുന്നതു കൊണ്ട് $ \mathbf {MRS_{x1x2} \,= \,-\,\frac{Δx_2}{Δx_1}} $ എന്ന് എഴുതാം.

അപചയ സീമാന്ത പ്രതിസ്ഥാപന നിരക്ക് ( Diminishing Marginal Rate of Sub stitution – DMRS )
ഉപഭോക്താവ് നിസംഗതാവക്രത്തിൽ മുകളിൽ നിന്ന് താഴേക്ക് വരുന്തോറും സാധനം 1 ന്റെ അളവ് കൂടുകയും സാധനം 2 ന്റെ അളവ് കുറയുകയും ചെയ്യുന്നു. സാധനം 1 ഉം സാധനം 2 ഉം തമ്മിലുള്ള സീമാന്ത പ്രതിസ്ഥാപന നിരക്ക് കുറഞ്ഞ് കുറഞ്ഞ് വരുന്നു. ഇതിനെ അപചയ സീമാന്ത പ്രതിസ്ഥാപന നിരക്ക് എന്ന് പറയുന്നു. പട്ടിക 2.3 ൽ a എന്ന ഉപഭോഗ ബണ്ടിലിൽനിന്ന് b , c , d , e എന്ന ഉപഭോഗ ബണ്ടിലിൽ ബണ്ടിലിൽ എത്തുമ്പോൾ MRS_x1,x2 4 , 3 , 2 , 1 എന്നിങ്ങനെ കുറഞ്ഞ് കുറഞ്ഞ് വരുന്നത് കാണാം.

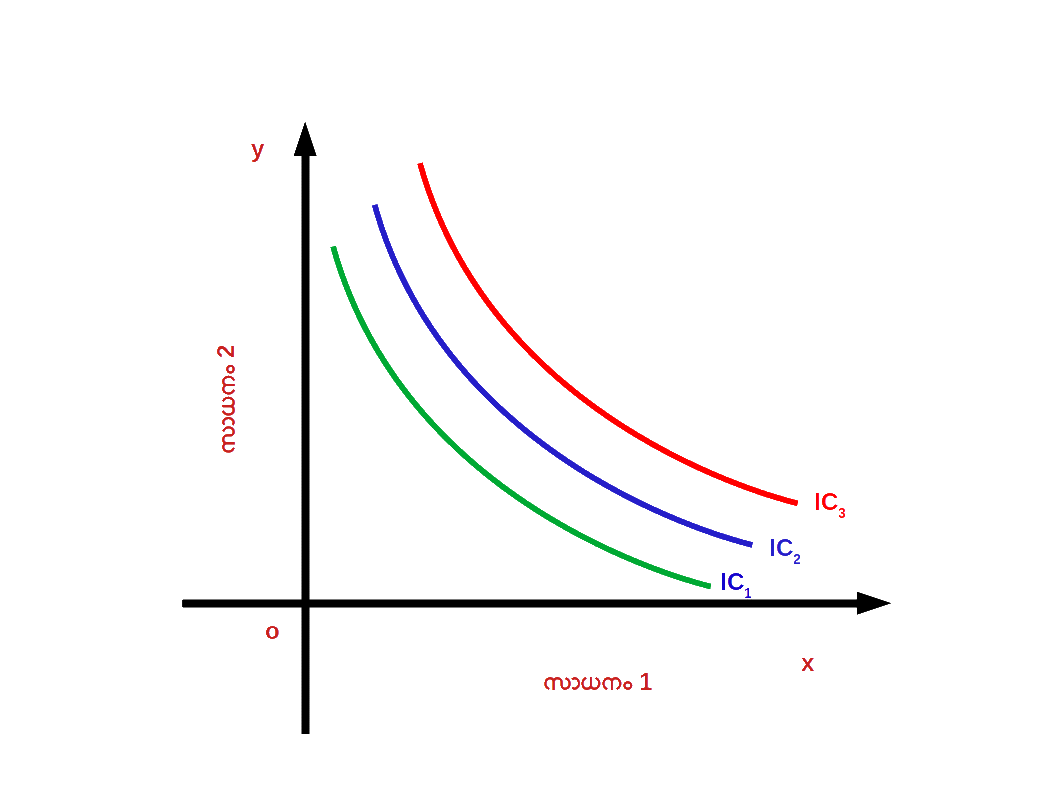
നിസംഗതാഭൂപടം ( Indifference Map )
നിസംഗതാവക്രങ്ങളുടെ ഒരു സമാഹാരത്തിന് നിസംഗതാഭൂപടം എന്ന് പറയുന്നു. അതായത് ഒരു കൂട്ടം നിസംഗതാവക്രങ്ങളെ നിസംഗതാ ഭൂപടം എന്നു വിളിക്കുന്നു. ഡയഗ്രം 2.19 ഒരു നിസംഗതാഭൂപടത്തെ കാണിക്കുന്നു.

Diagram 2.18

IC₁ , IC₂ , IC₃ എന്നീ നിസംഗതാവക്രത്തിലുള്ള ഉപഭോഗ ബണ്ടിലിൽ നിന്നുള്ള സംതൃപ്തി വ്യത്യസ്തമായിരിക്കും. IC₁ എന്ന നിസംഗതാവക്രത്തെക്കാൾ ഉയർന്ന സംതൃപ്തിയാണ് IC₂ എന്ന നിസംഗതാവക്രത്തിൽനിന്ന് ലഭിക്കുന്നത് . IC₂ എന്ന നിസംഗതാവക്രത്തെക്കാൾ ഉയർന്ന സംതൃപ്തി IC₃ യിൽനിന്ന് ലഭിക്കുന്നു.
നിസംഗതാവകത്തിന്റെ പ്രത്യേകതകൾ ( Properties of Indifference Curve )

1. നിസ്സംഗത വക്രങ്ങൾ ഇടത്തുനിന്ന് വലത്തോട്ട് താഴേക്ക് ചരിഞ്ഞുകിടക്കുന്നു.

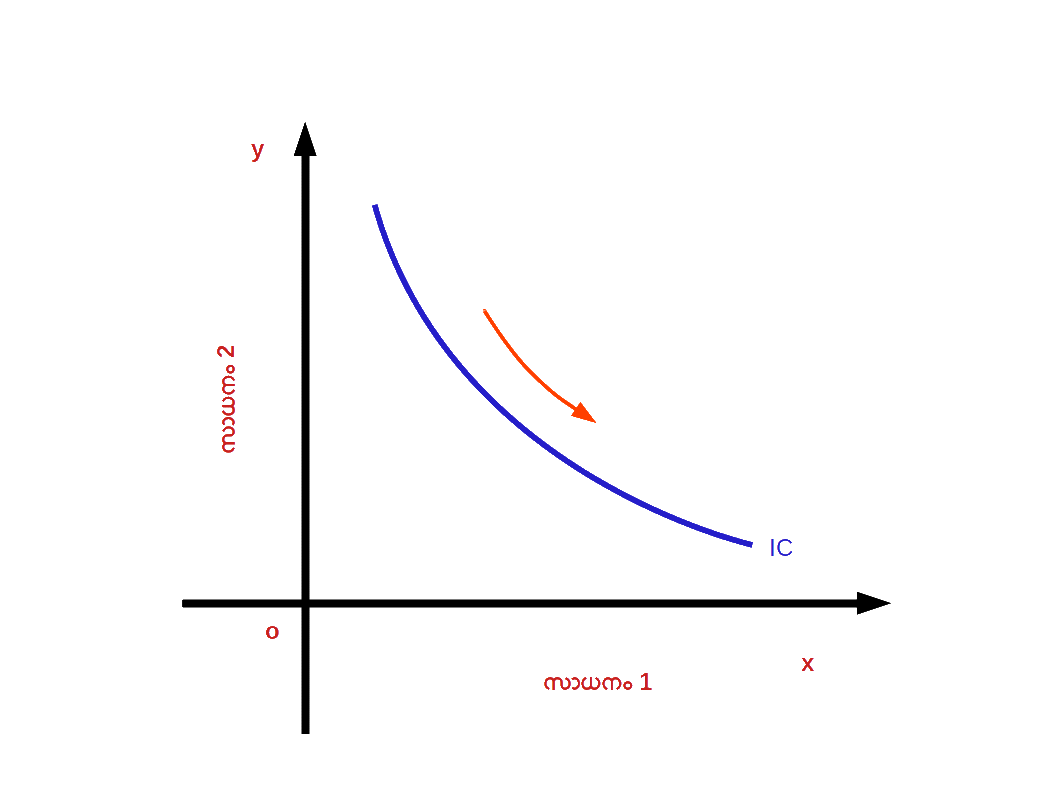
2. നിസംഗതാവക്രം ഉന്മധ്യമാണ്:
നിസംഗതാവക്രങ്ങൾ മൂലത്തിലേക്ക് ( origin ) ഉന്മധ്യമാണ്.

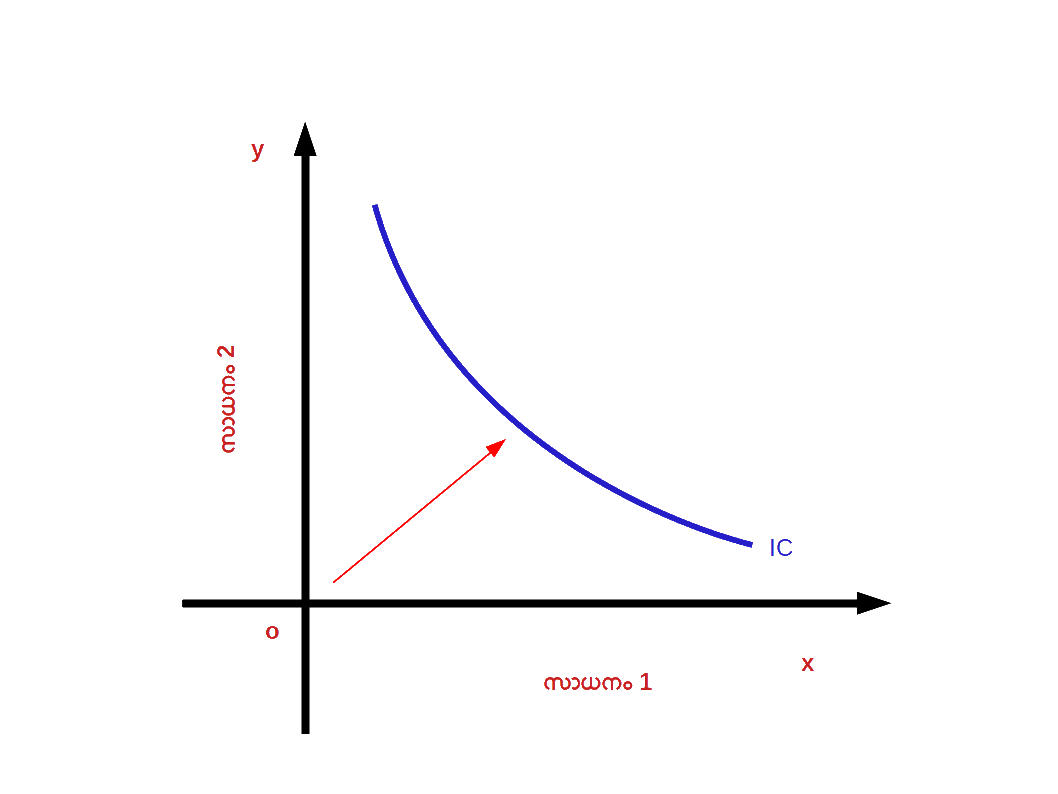
3. ഉയർന്ന തലത്തിലുള്ള നിസംഗതാവക്രങ്ങൾ ഉയർന്ന സംതൃപ്തിയെ പ്രതിനിധാനം ചെയ്യുന്നു:
വലതുഭാഗത്തുള്ള നിസംഗതാവക്രം ഉയർന്ന സംതൃപ്തിയെയും ഇടതുഭാഗത്തുള്ള നിസംഗതാവക്രം താഴ്ന്ന സംതൃപ്തിയെയും സൂചിപ്പിക്കുന്നു . നിസംഗതാ ഭൂപടത്തിൽ IC₁ നെക്കാൾ സംതൃപ്തി IC₂ ൽ നിന്ന് ലഭിക്കുന്നു . IC₂ നെക്കാൾ സംതൃപ്തി IC₃ ൽ നിന്ന് ലഭിക്കുന്നു.

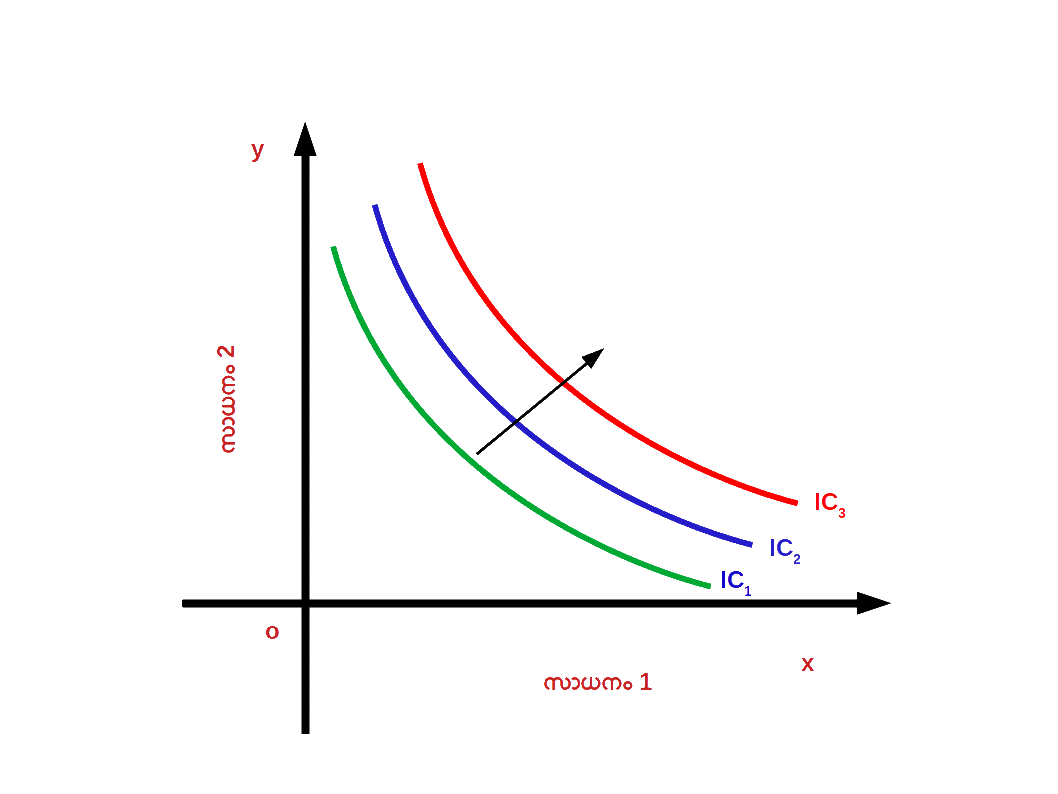
4. നിസംഗതാവക്രങ്ങൾ ഒരിക്കലും പരസ്പരം ഛേദിദിക്കില്ല:
താഴെ കൊടുത്തിരിക്കുന്നതു പോലെ IC₁ ഉം IC₂ ഉം പരസ്പരം ഛേദിക്കുകയില്ല.

ഉപയുക്തതാ ധർമ്മം (Utility Function)

മനുഷ്യന്റെ ആവശ്യങ്ങളെ തൃപ്തിപ്പെടുത്താനുള്ള ഒരു വസ്തുവിന്റെ കഴിവിനെയാണ് ഉപയുക്തത എന്നു പറയുന്നത്.

ബണ്ടിലുകളുടെ റാങ്കിങ് നിലനിർത്തുന്ന രീതിയിൽ ബണ്ടിലുകൾക്ക് നമ്പറുകൾ നല്കി ഉപഭോക്താവിന് ബണ്ടിലുകളോടുള്ള മുൻഗണനകൾ പ്രതിപാദിക്കാൻ കഴിയും. ഉപയുക്തതാ നമ്പറുകളെ അടി സ്ഥാനമാക്കിയുള്ള ബണ്ടിലുകളുടെ മുൻഗണനകളുടെ പ്രാതിനിധ്യത്തെ ഉപയുക്തതാ ധർമ്മം അഥവാ ഉപയുക്തതാ പ്രദർശനം എന്നു പറയുന്നു.
ഏറ്റവും മുൻഗണന നല്കുന്ന ബണ്ടിലിന് ഉയർന്ന യൂട്ടിലിറ്റി നമ്പറുകളും കുറഞ്ഞ മുൻഗണന നല്കുന്ന ബണ്ടിലിന് താഴ്ന്ന യൂട്ടിലിറ്റി നമ്പറുകളും നല്കുന്നു. നിസംഗതമായ ബണ്ടിലുകൾക്ക് ഒരേ യൂട്ടിലിറ്റി നമ്പറുകളായിരിക്കും നല്കുക. പട്ടിക 2.4 ൽ വിവിധ ബണ്ടിലുകളുടെ ഉപയുക്തതാ ധർമ്മങ്ങൾ പ്രദർശിപ്പിച്ചിരിക്കുന്നു.

Table 2.4

രണ്ട് സാധനങ്ങളുടെ ബണ്ടിലുകൾ ഉപയുക്തത പ്രാതിനിധ്യം

(2, 2) 40 units

(1, 3), (3, 1), 0, 4), (4, 0) 35 units

(1, 2), (2, 1), (0, 3), (3; 0) 28 units

(0, 2), (2, 0), (1, 1) 20 units

(0, 0), (0, 1), (1, 0) 10 units

( 2 , 2 ) എന്ന ബണ്ടിലിന് നല്കിയിരിക്കുന്ന യൂട്ടിലിറ്റി നമ്പർ 40 ആണ്. ( 1 , 3 ) , ( 3 , 1 ) , ( 0 , 4 ) , ( 4 , 0 ) എന്നിവയ്ക്ക് നല്കിയിരിക്കുന്ന യൂട്ടിലിറ്റി നമ്പർ 35 ആണ്. ( 1 , 2 ) , ( 2 , 1 ) , ( 0 , 3 ) , ( 3 , 0 ) എന്നിവയ്ക്ക് നല്കിയിരിക്കുന്ന യൂട്ടിലിറ്റി നമ്പർ 28 ആണ്. ഇതിങ്ങനെ തുടരുന്നു. ഇവയിൽ ഏറ്റവും മുൻഗണന നല്കുന്ന ബണ്ടിൽ ( 2 , 2 ) ആയതിനാൽ അതിന്റെ യൂട്ടിലിറ്റി നമ്പർ ഏറ്റവും ഉയർന്നതാണ്. ഏറ്റവും കുറഞ്ഞ മുൻഗണന നല്കുന്ന ബണ്ടിൽ ( 0 , 1 ) , ( 1 , 0 ) , ( 0 , 0 ) എന്നിവയായതുകൊണ്ട് അവയുടെ യൂട്ടിലിറ്റി നമ്പർ 10 ആണ്.

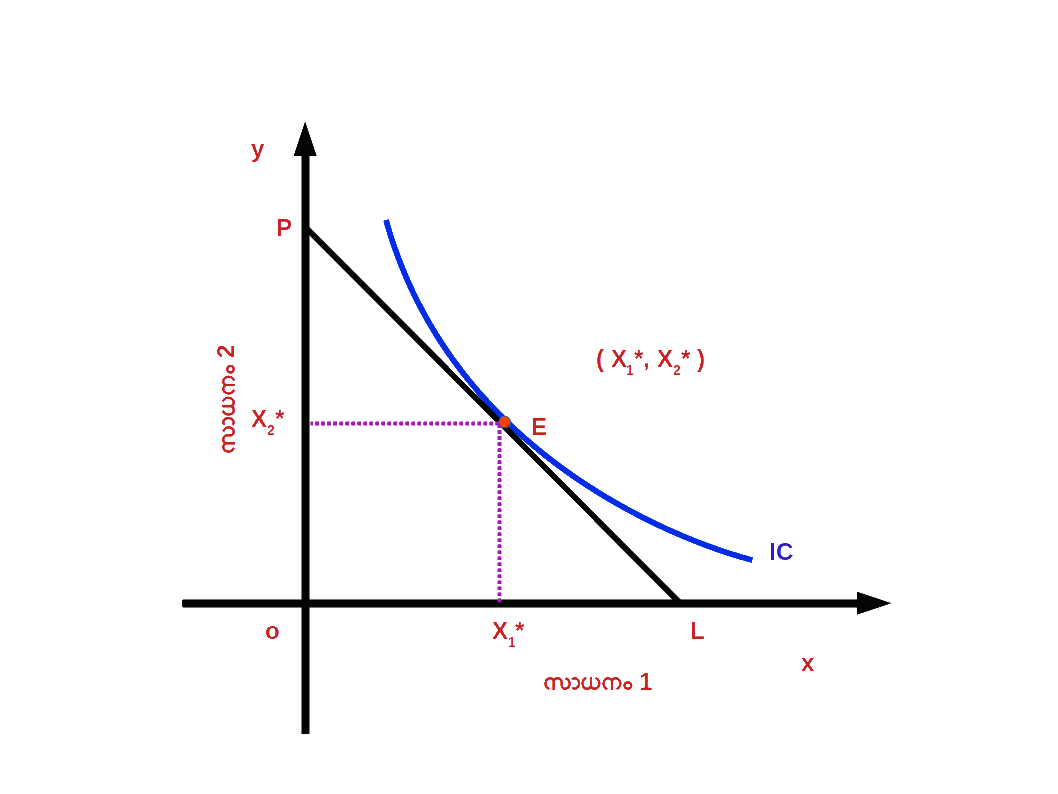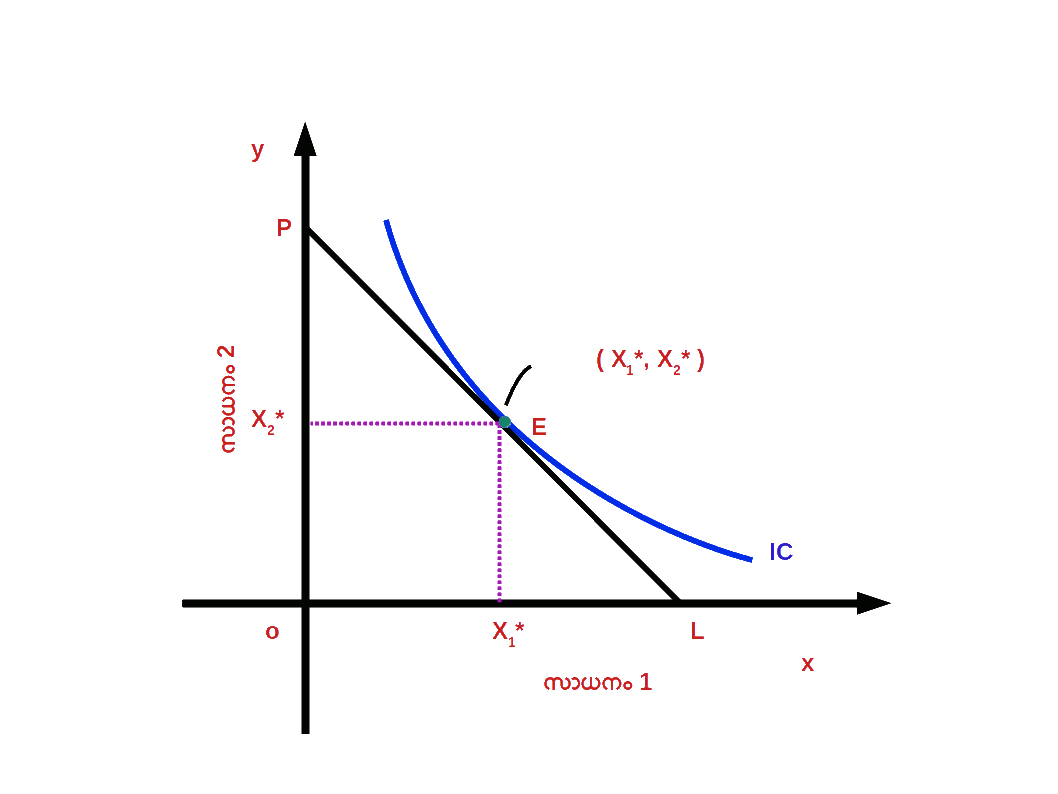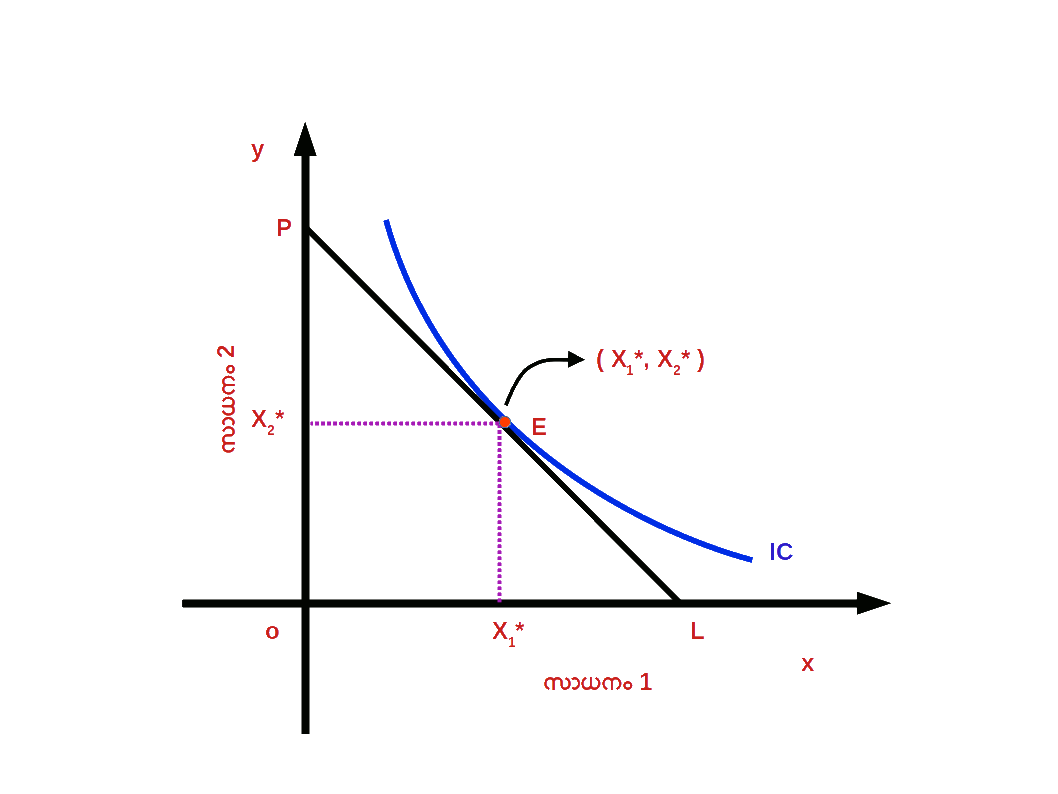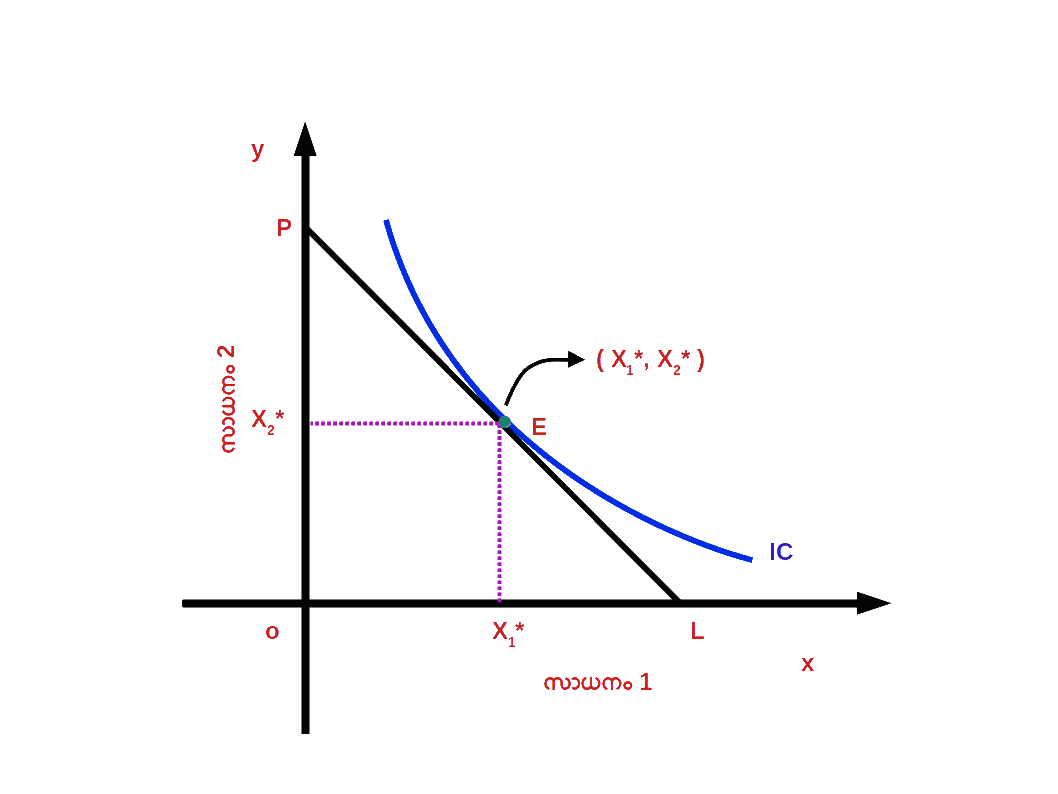
ഉപഭോക്താവിന്റെ സന്തുലിതാവസ്ഥ ( Consumer’s Equilibrium )
സാധനങ്ങളും സേവനങ്ങളും വാങ്ങുന്നതിലൂടെ തന്റെ സംതൃപ്തി പരമാവധിയാക്കുകയെന്ന ലക്ഷ്യത്തോടെ ഉപഭോക്താവ് കമ്പോളത്തിൽ പെരുമാറുന്നു. യുക്തിപരമായി ചിന്തിക്കുന്ന ഒരു വ്യക്തി തനിക്ക് പരമാവധി സംതൃപ്തി ലഭിക്കുന്ന വിധത്തിൽ തന്റെ പണം ചെലവഴിക്കുന്നു. ഉപഭോക്താവിന് ഏറ്റവും കൂടുതൽ സംതൃപ്തി ലഭിക്കുന്ന അവസ്ഥയാണ് ഉപഭോക്താവിന്റെ സന്തുലിതാവസ്ഥ എന്നു പറയുന്നത്. ഒരു ഉപഭോക്താവിന് ലഭ്യമായ ഉപഭോഗ ബണ്ടിലുകളും വരുമാനവും വെച്ച് ഏറ്റവും അഥവാ പരമാവധി സംതൃപ്തി ലഭിക്കുന്ന അവസ്ഥയാണിത്.
ഒരേ സംതൃപ്തി നല്കുന്ന ഒരു കൂട്ടം ബണ്ടിലുകളെ നിസംഗതാ പ്രതിനിധാനം ചെയ്യുന്നു. അതുപോലെ ഉപഭോക്താവ് തന്റെ വരുമാനം പൂർണ്ണമായി ചെലവഴിച്ചുകൊണ്ട് ലഭ്യമാകുന്ന ഒരു കൂട്ടം ബണ്ടിലുകളെ ബജറ്റ് രേഖ പ്രതിനിധാനം ചെയ്യുന്നു . ഉപഭോക്താവ് തന്റെ വരുമാന പരിധിക്കുള്ളിൽ നിന്നു കൊണ്ട് തനിക്ക് ഏറ്റവും കൂടുതൽ സംതൃപ്തി ലഭിക്കുന്ന ബണ്ടിൽ തെരഞ്ഞെടുക്കുന്നു. നിസംഗതാ സമീപനമനുസരിച്ച് , ബജറ്റ് രേഖ നിസംഗതാ വക്രത്തിൽ സ്പർശിക്കുന്ന ( tangent ) ബിന്ദുവിലുള്ള ഉപഭോഗ ബണ്ടിലാണ് ഉപഭോക്താവിന് പരമാവധി സംതൃപ്തി ലഭിക്കുന്ന ബണ്ടിൽ മറ്റൊരു വിധത്തിൽ പറഞ്ഞാൽ , ബജറ്റ് രേഖയുടെ ചെരിവും നിസംഗതാവക്രത്തിന്റെ ചെരിവും തുല്യമാകുന്ന ബിന്ദുവിലുള്ള ഉപഭോഗ ബണ്ടിലാണ് ഉപഭോക്താവിന് പരമാവധി സംതൃപ്തി ലഭിക്കുന്ന ബണ്ടിൽ. ഡയഗ്രം 2.19 ൽ BL എന്നത് ബജറ്റ് രേഖയും IC₁ , IC₂ , IC₃ എന്നത് വിവിധ നിസംഗതാവക്രവുമാണ്. E എന്ന ബിന്ദുവിൽ ബജറ്റ് രേഖയുടെ ചെരിവും IC₂ ന്റെ ചെരിവും തുല്യമാണ്. $\biggl({\frac{Δx_{2}}{Δx_{1}}}\, = MRS_{x1,x2} =\,{\frac{P_{1}}{P_{2}}} \biggr)$. E എന്ന ബിന്ദുവിൽ ഉപഭോക്താവ് സന്തുലിതാവസ്ഥയിലാണ്. ഉപഭോക്താവ് (x^*₁ , x^*₂ ) എന്ന ഉപഭോഗ ബണ്ടിൽ തെരഞ്ഞെടുത്തുകൊണ്ട് തന്റെ സംതൃപ്തി പരമാവധിയാക്കുന്നു.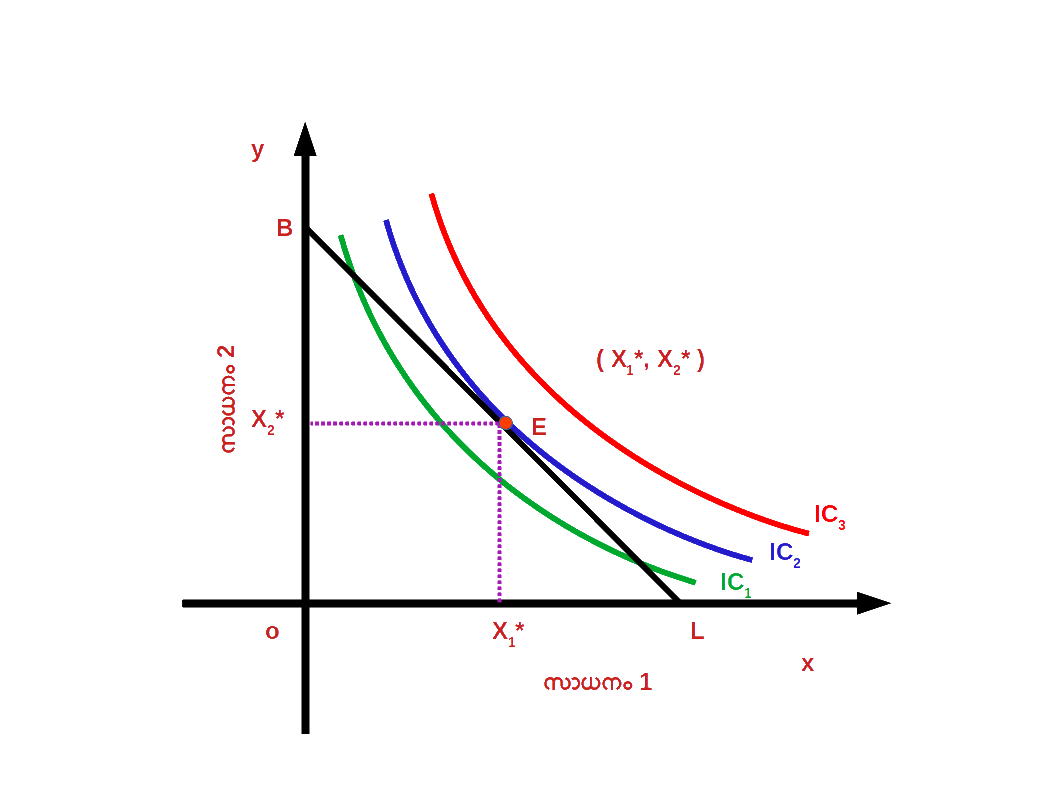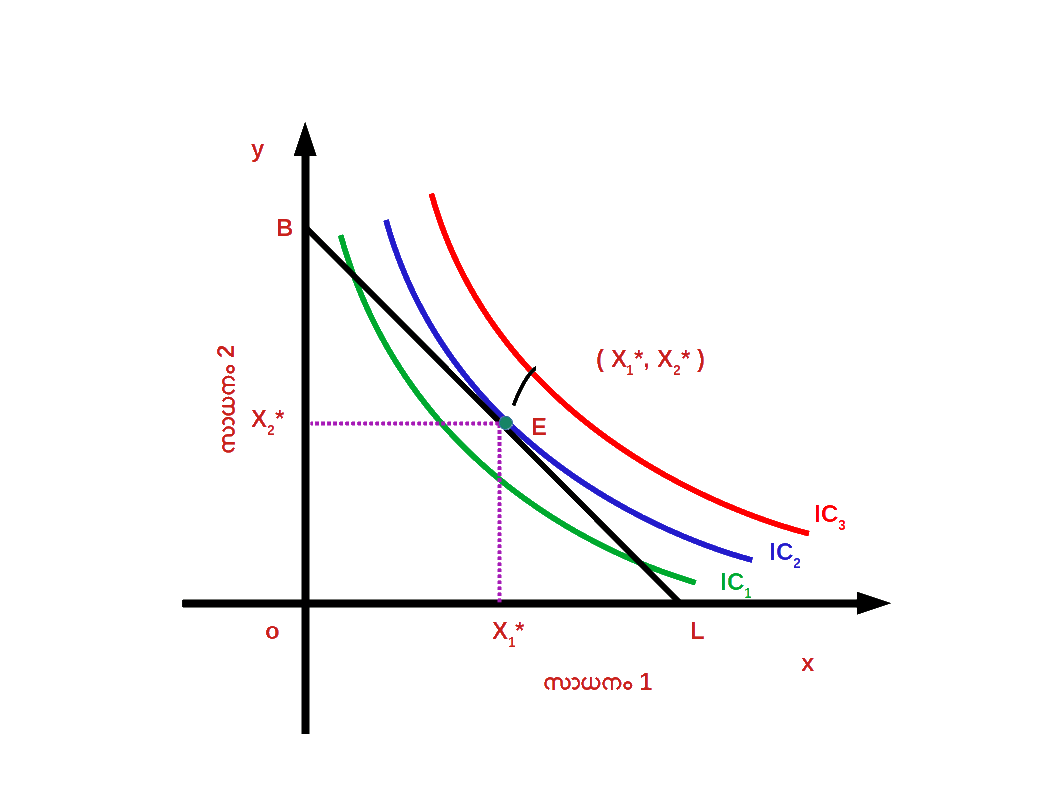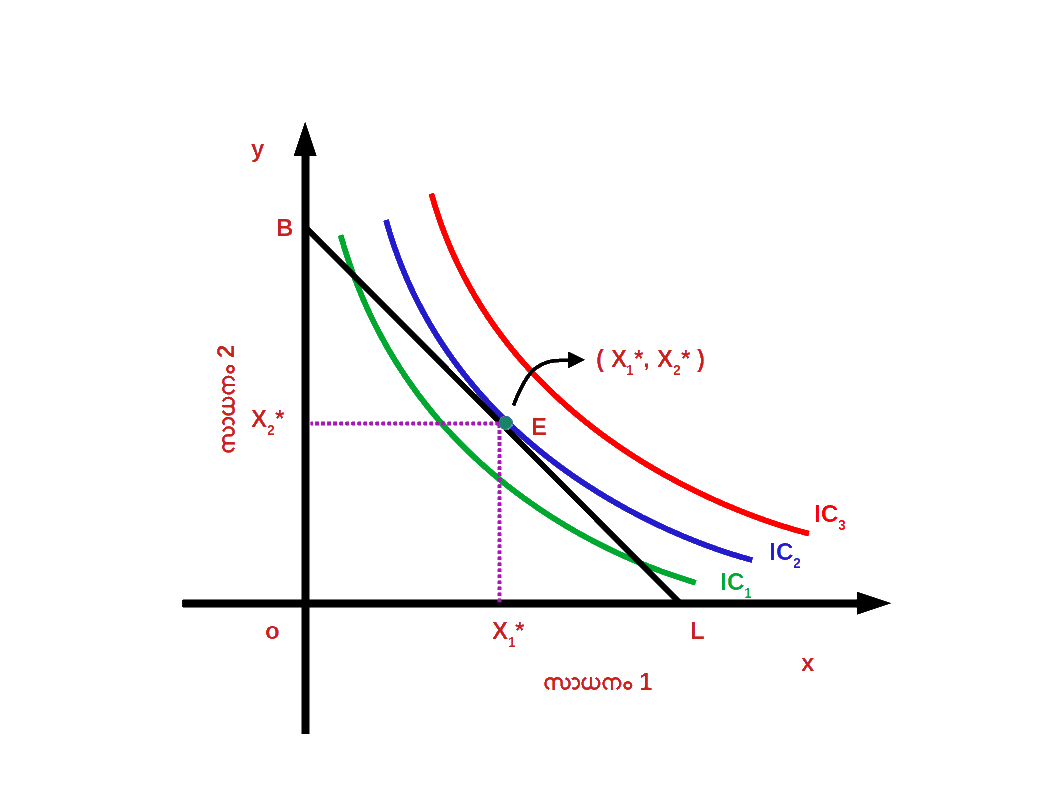

Diagram 2.18

IC₁ എന്ന നിസംഗതാവക്രത്തിലുള്ള ഉപഭോഗ ബണ്ടിലുകൾ IC₂ എന്ന നിസംഗതാവക്രത്തിലുള്ള ഉപഭോഗ ബണ്ടിലിനെക്കാളും കുറഞ്ഞ സംതൃപ്തിയാണ് നല്കുന്നത്. IC₃ എന്ന നിസംഗതാവക്രത്തിലുള്ള ഉപഭോഗ ബണ്ടിൽ IC₂ നെക്കാൾ ഉയർന്ന സംതൃപ്തി നല്കുന്നുണ്ടെങ്കിലും ഉപഭോക്താവിന് IC₃ ലുള്ള ഉപഭോഗ ബണ്ടിൽ നേടാൻ കഴിയുകയില്ല. എന്തുകൊണ്ടെന്നാൽ , IC₃ ലുള്ള എല്ലാ ഉപഭോഗ ബണ്ടിലുകളും തന്റെ ബജറ്റ് രേഖയ്ക്ക് , വരുമാന പരിധിക്ക് പുറത്താണ്. അതുകൊണ്ട് ഉപഭോക്താ വിന് ഏറ്റവും സംതൃപ്തി നല്കുന്ന ബണ്ടിൽ (x^*₁ , x^*₂ )ആണ്.

ചോദനം ( Demand )
സാധാരണയായി ഡിമാന്റ് എന്നു പറഞ്ഞാൽ നാം ഉദ്ദേശിക്കുന്നത് ഒരു ഉപഭോക്താവിന് ഒരു സാധനം വാങ്ങാനുള്ള ആഗ്രഹത്തെയാണ്. എന്നാൽ സാമ്പത്തിക ശാസ്ത്രത്തിൽ ആഗ്രഹം മാത്രമായാൽ ഡിമാന്റ് ആവുകയില്ല. ആഗ്രഹത്തോടൊപ്പം വില കൊടുക്കാനുള്ള കഴിവും സന്നദ്ധതയുമുണ്ടാകണം. അപ്പോൾ ഒരു സാധനം വില കൊടുത്ത് വാങ്ങാനുള്ള കഴിവ് , സന്നദ്ധത എന്നിവയുടെ പിൻബലത്തോട് കൂടിയ ഒരു ഉപഭോക്താവിന്റെ ആഗ്രഹത്തെയാണ് ഡിമാന്റ് എന്നു പറയുന്നത്.

ഒരു ചരക്കിനുള്ള ചോദനം ( Demand for a Commodity )
ഒരു നിശ്ചിത വിലയ്ക്ക് ഒരു നിശ്ചിത കാലയളവിനുള്ളിൽ ഉപഭോക്താക്കൾ കമ്പോളത്തിൽ നിന്ന് വാങ്ങാൻ തയ്യാറുള്ള സാധനത്തിന്റെ അളവിനെയാണ് ചരക്കിന്റെ ചോദനം എന്നു പറയുന്നത്. ഉപഭോക്താവ് വാങ്ങാൻ നിശ്ചയിക്കുന്ന സാധനത്തിന്റെ അളവ് പ്രധാനമായും ആ സാധന ത്തിന്റെ വില , പ്രതിസ്ഥാപന വസ്തുക്കളുടെ വില , ഉപഭോക്താവിന്റെ വരുമാനം , ഉപഭോക്താവിന്റെ അഭിരുചിയും മുൻഗണനകളും എന്നിവയെ ആശ്രയിച്ചിരിക്കുന്നു.

വ്യക്തിഗത ചോദനം ( Individual Demand )

ഒരു നിശ്ചിത സമയത്ത് , ഒരു നിശ്ചിത വിലയ്ക്ക് ഒരു വ്യക്തി കമ്പോളത്തിൽ നിന്ന് വാങ്ങാൻ തയ്യാറുള്ള സാധനത്തിന്റെ അളവാണ് വ്യക്തിഗത ചോദനം.

ചോദന ധർമ്മം ( Demand Function )
ചോദനവും ചോദനത്തെ നിർണ്ണയിക്കുന്ന ഘടകങ്ങളും തമ്മിലുള്ള ബന്ധത്തെ ചോദന ധർമ്മം എന്നു പറയുന്നു. അതായത് , ചോദനവും ( q ) അതിനെ ബാധിക്കുന്ന ഘടകങ്ങളായ സാധനത്തിന്റെ വില ( P ) , ഉപഭോക്താവിന്റെ വരുമാനം ( M ) , ബന്ധപ്പെട്ട സാധനത്തിന്റെ വില ( Pr ) , ഉപഭോക്താവിന്റെ അഭിരുചിയും താല്പര്യങ്ങളും ( T ) തുടങ്ങിയവയും തമ്മിലുള്ള ബന്ധത്തെ ചോദന ധർമ്മം എന്നു വിളിക്കുന്നു. ചോദന ധർമ്മത്തെ ബീജഗണിത രൂപത്തിൽ താഴെ നൽകിയ രീതിയിൽ നിർവചിക്കാം :

q = f(P, P_r, M , T

ചോദനത്തെ നിർണ്ണയിക്കുന്ന വിവിധ ഘടകങ്ങളിൽ ഏറ്റവും പ്രധാനപ്പെട്ടത് ആ സാധനത്തിന്റെ വിലയാണ് ( P ). അതുകൊണ്ട് ഉപഭോക്താവിന്റെ ഒരു സാധനത്തോടുള്ള ചോദനത്തെ വിലയുടെ ധർമ്മമായി എഴുതാം.

q = d(P)

ചോദന നിയമം ( Law of Demand )
പൊതുവേ ഒരു സാധനത്തിനുള്ള ഉപഭോക്താവിന്റെ ചോദനവും ആ സാധനത്തിന്റെ വിലയും തമ്മിലുള്ള ബന്ധം വിപരീത ( inverse or negative ) മായിരിക്കും . ഒരു സാധനത്തിന്റെ ചോദനവും വിലയും തമ്മിലുള്ള വിപരീത ബന്ധത്തെ ചോദന നിയമം എന്നു പറയുന്നു. അതായത് , മറ്റു ഘടകങ്ങളിൽ മാറ്റമില്ലെങ്കിൽ ഒരു സാധനത്തിന്റെ വില കുറയുമ്പോൾ ചോദനത്തിന്റെ അളവ് വർധിക്കുകയും വില കൂടുമ്പോൾ ചോദനത്തിന്റെ അളവ് കുറയുകയും ചെയ്യുന്നതിനെയാണ് ചോദന നിയമം എന്നു പറയുന്നത്. ഉപഭോക്താവിന്റെ വരുമാനം , ബന്ധപ്പെട്ട മറ്റു സാധനങ്ങളുടെ വിലകൾ , ഉപഭോക്താവിന്റെ അഭിരുചിയും താല്പര്യങ്ങളും തുടങ്ങിയ ഘടകങ്ങളിൽ മാറ്റമില്ലാതെ തുടരുമെന്ന സങ്കല്പത്തിലധിഷ്ഠിതമാണ് ചോദന നിയമം.

ചോദന വക്രം ( Demand Curve )
ചോദന ധർമ്മത്തെ ഒരു ഗ്രാഫിലൂടെ പ്രദർശിപ്പിക്കാം. ചോദന ധർമ്മത്തിന്റെ ചോദനവും വിലയും തമ്മിലുള്ള വിപരീത ബന്ധം കാണിക്കുന്ന ഗ്രാഫിനെ ( വക്രത്തെ ) ചോദന വക്രം എന്നു പറയുന്നു. ഇത് താഴെ ഡയഗ്രം 2.19 ൽ കൊടുത്തിരിക്കുന്നു.

Diagram 2.19

ഡയഗ്രം 2.19 – ൽ x – അക്ഷത്തിൽ ചോദനത്തിന്റെ അളവും y അക്ഷത്തിൽ സാധനത്തിന്റെ വിലയും കാണിച്ചിരിക്കുന്നു.q = d ( P ) എന്നതാണ് ചോദന വക്രം.ഈ വക്രം ചോദനവും വിലയും തമ്മിലുള്ള വിപരീത ബന്ധം സൂചിപ്പിക്കുന്നു. വില OP₁ ൽ നിന്ന് OP ആയി വർദ്ധിച്ചപ്പോൾ ചോദനത്തിന്റെ അളവ് Oq₁ ൽ നിന്ന് Oq ആയി കുറഞ്ഞിരിക്കുന്നു. വില OP യിൽ നിന്ന് OP₁ ആയി കുറഞ്ഞപ്പോൾ ചോദനത്തിന്റെ അളവ് Oq ൽ നിന്ന് Oq₁ ആയി വർദ്ധിച്ചിരിക്കുന്നു. അപ്പോൾ , q = d( P ) എന്ന വക്രം ചോദനത്തിന്റെ അളവും വിലയും തമ്മിലുള്ള വിപരീത ബന്ധത്തെ സൂചിപ്പിക്കുന്നു. അതു കൊണ്ടാണ് ചോദന വക്രം ഇടത്ത് മുകളിൽനിന്ന് താഴെ വലത്തോട്ട് ചെരിഞ്ഞിരിക്കുന്നത്. ചോദന വക്രത്തിന് നെഗറ്റീവ് ചെരിവാണ്.

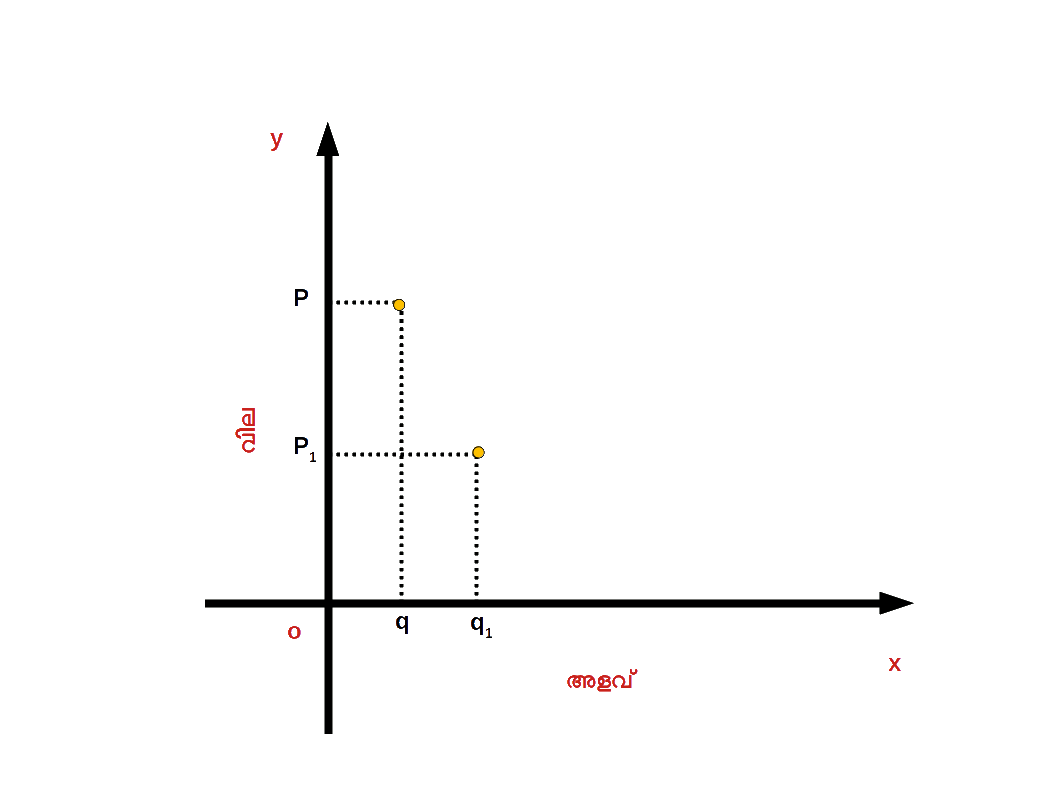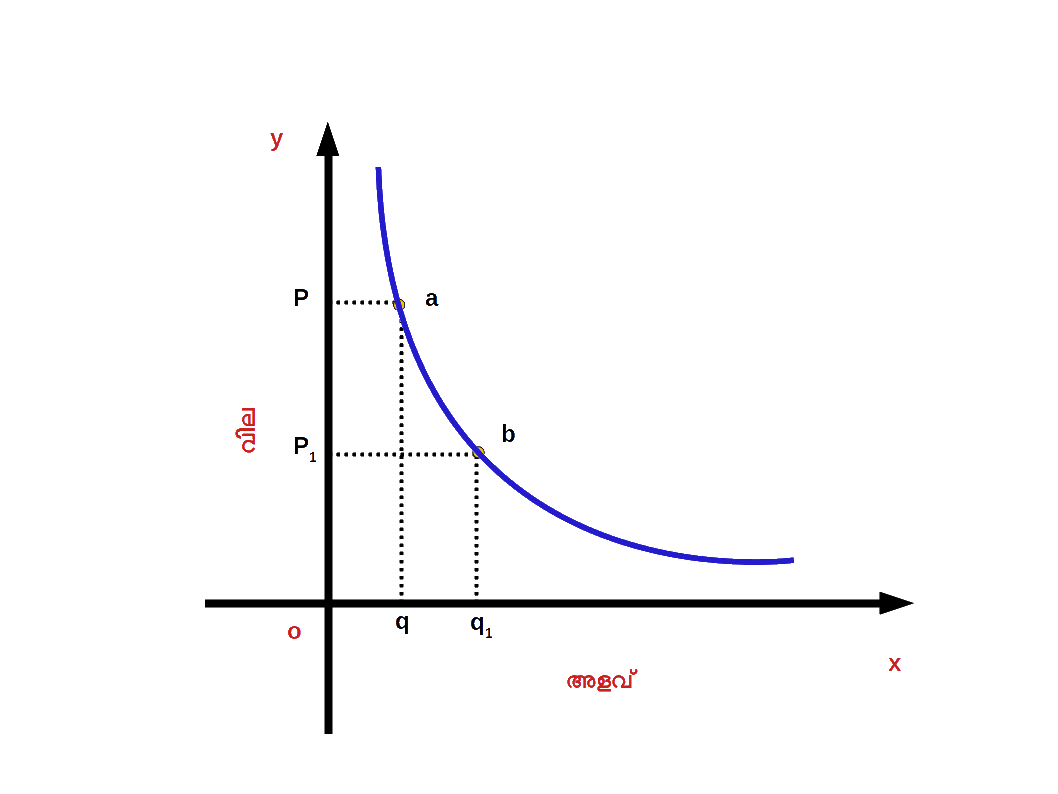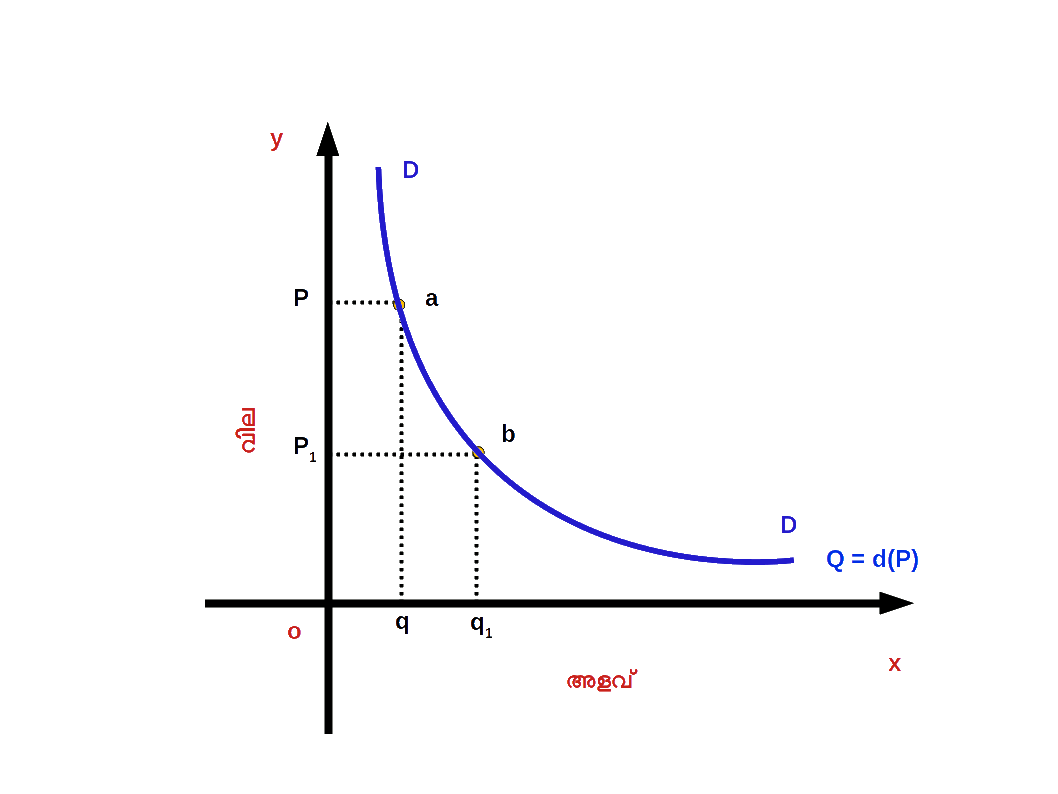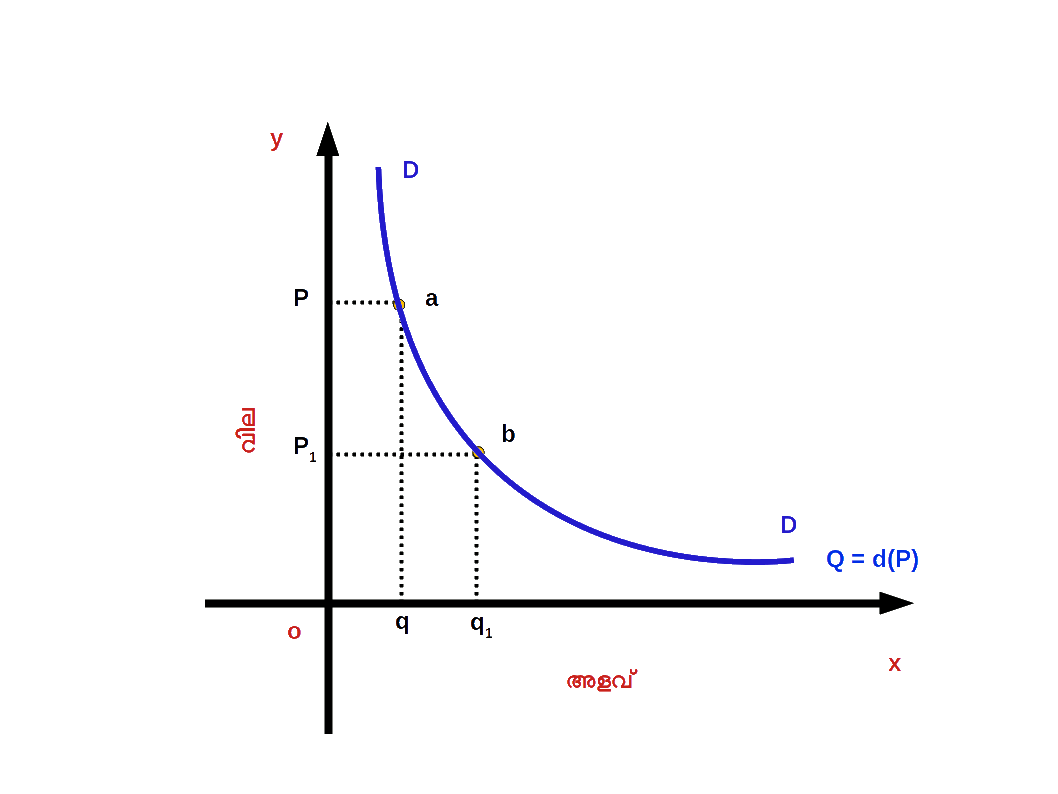
വില കുറയുമ്പോൾ ചോദനം കൂടുന്നതെന്തുകൊണ്ട് ? അല്ലെങ്കിൽ എന്തുകൊണ്ടാണ് ചോദന വക്രം താഴോട്ട് ചെരിഞ്ഞിറങ്ങുന്നത് ?
വില കുറയുമ്പോൾ ചോദനം കൂടുകയും വില കൂടുമ്പോൾ ചോദനം കുറയുകയും ചെയ്യുന്നു. ഇതിന് പ്രധാനമായും രണ്ട് കാരണങ്ങളാണുള്ളത്.

( 1 ) പ്രതിസ്ഥാപന പ്രഭാവം

( 2 ) വരുമാന പ്രഭാവം

ഇത് താഴെ പറയുന്നതുപോലെ വിവരിക്കാം.

വില പ്രഭാവം ( Price effect )

വിലയിലുണ്ടായ മാറ്റത്തിന്റെ ഫലമായി ചോദനത്തിൽ വന്ന മാറ്റത്തെ വില പ്രഭാവം എന്നു പറയുന്നു. വില പ്രഭാവത്തെ പ്രതിസ്ഥാപന പ്രഭാവമെന്നും വരുമാന പ്രഭാവമെന്നും രണ്ടായി വിഭജിച്ചിരിക്കുന്നു.

പ്രതിസ്ഥാപന പ്രഭാവം ( Substitution effect )

ഉപഭോക്താവിന്റെ യഥാർത്ഥ വരുമാനത്തിൽ മാറ്റമില്ലാതെ ആപേക്ഷിക വില ( relative price ) യിലുണ്ടായ മാറ്റത്തിന്റെ ഫലമായി ഒരു സാധനത്തിന്റെ ചോദനത്തിലുള്ള മാറ്റത്തെ പ്രതിസ്ഥാപന പ്രഭാവമെന്നു പറയുന്നു. രണ്ട് സാധനങ്ങളിൽ ഒന്നിന്റെ വില കുറയുമ്പോൾ ആപേക്ഷിക വിലയിൽ മാറ്റം വരുന്നു. തന്മൂലം വില കുറഞ്ഞ സാധനത്തിന്റെ കൂടുതൽ അളവ് വിലയിൽ മാറ്റം വരാത്ത സാധനത്തിന് പകരം ചോദനം ചെയ്യുന്നു അഥവാ പ്രതിസ്ഥാപനം ചെയ്യുന്നു.

വരുമാന പ്രഭാവം ( Income effect )

വിലയിലുള്ള മാറ്റത്തിന്റെ ഫലമായി ഉപഭോക്താവിന്റെ യഥാർത്ഥ വരുമാനത്തിലുള്ള മാറ്റം മൂലം ഒരു വസ്തുവിന്റെ ചോദനത്തിലുള്ള മാറ്റത്തെയാണ് വരുമാന പ്രഭാവമെന്നു പറയുന്നത്. സാധനത്തിന്റെ വില കുറയുമ്പോൾ ക്രയശേഷി ( purchasing power ) വർധിക്കുന്നു. ഇത് യഥാർത്ഥ വരുമാന വർധനവാണ് തന്മൂലം ഉപഭോക്താവ് കൂടുതൽ അളവ് സാധനം ചോദനം ചെയ്യപ്പെടുന്നു.

Diagram 2.20

ഡയഗ്രം 2.20 ൽ PL എന്ന ബജറ്റ് രേഖയിൽ E എന്ന ബിന്ദുവിൽ ഉപഭോക്താവ് സന്തുലിതാ വസ്ഥയിലാണ്. ബജറ്റ് രേഖ PL നിസംഗതാവക്രം IC യിൽ E എന്ന ബിന്ദുവിൽ സ്പർശിച്ചിരിക്കുന്നു . അയാളുടെ സന്തുലിത ബണ്ടിൽ (x^*₁ , x^*₂ ) ആണ്. ഈ ബണ്ടിലിന് വേണ്ടി വരുന്ന ചെലവ് P₁x*₁ + P₂x*₂ = M ആണ്.
രണ്ട് സാധനങ്ങളിൽ ഒന്നിന്റെ വില കുറയുമ്പോൾ രണ്ട് ഫലങ്ങളുണ്ടാകുന്നു. സാധനം 1 ന്റെ വില കുറയുന്നുവെന്ന് കരുതുക.

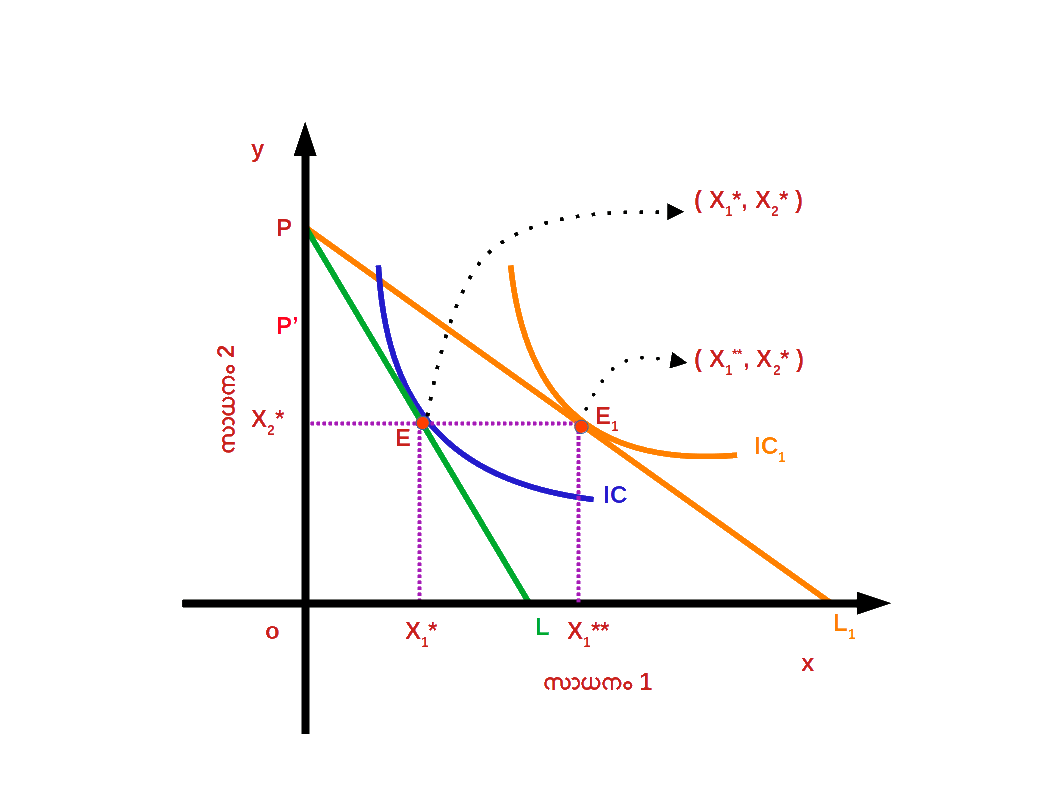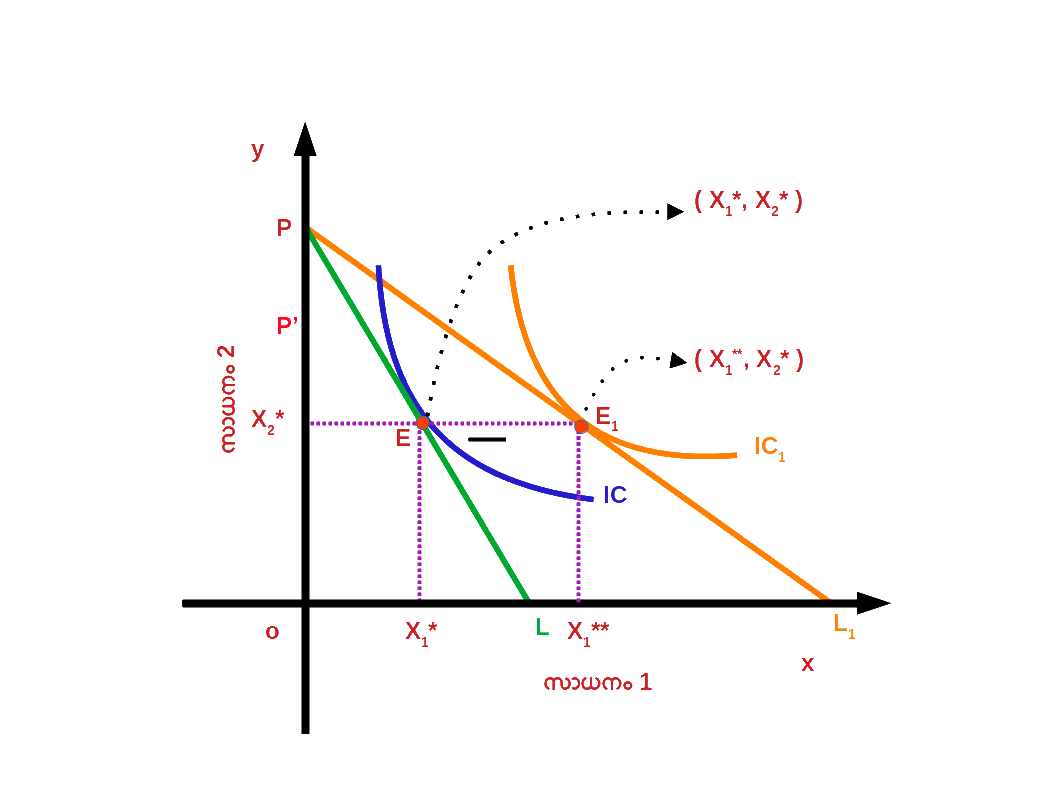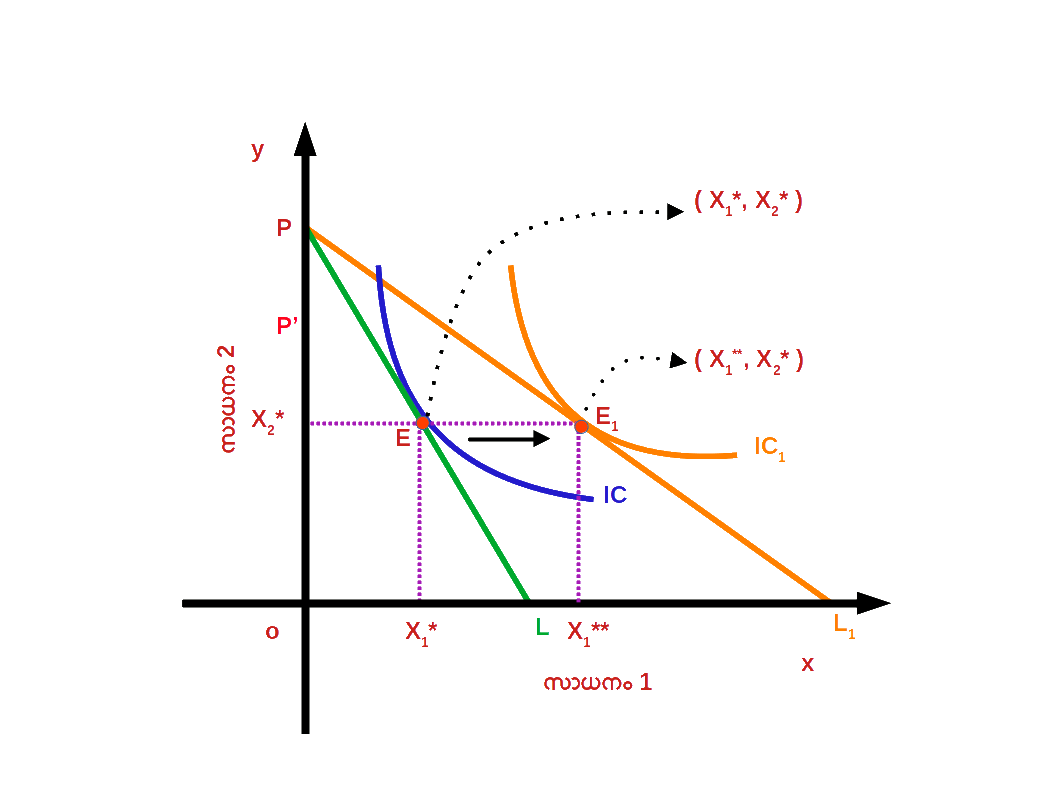
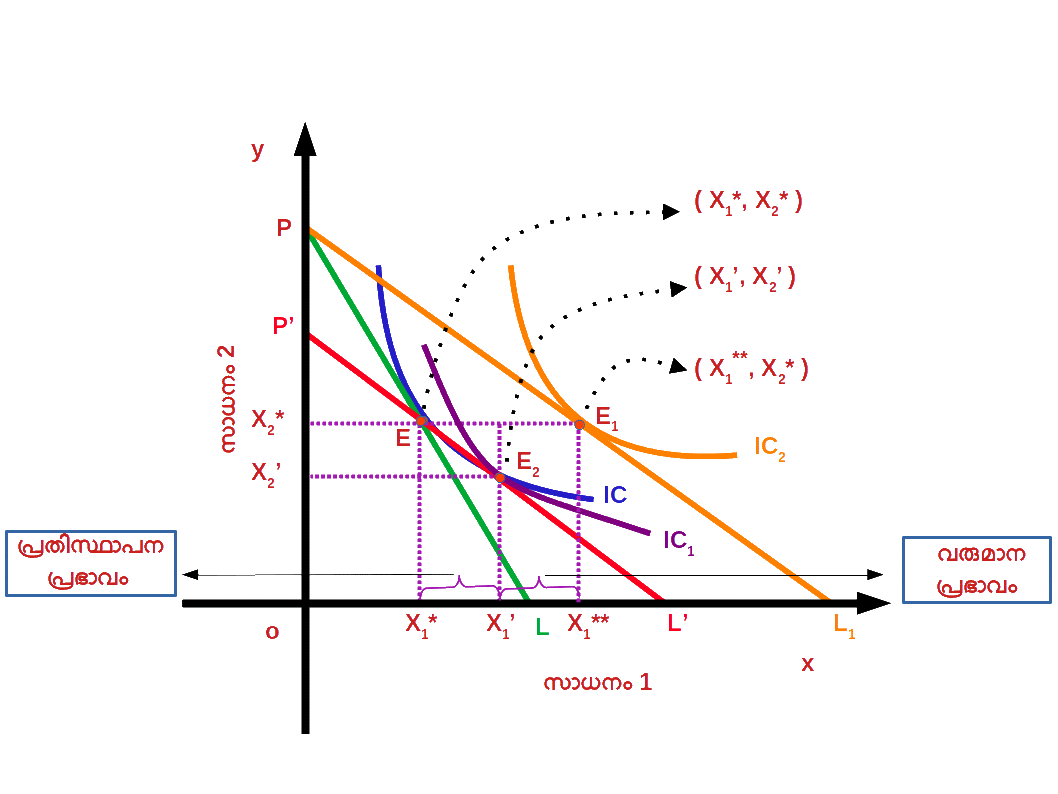
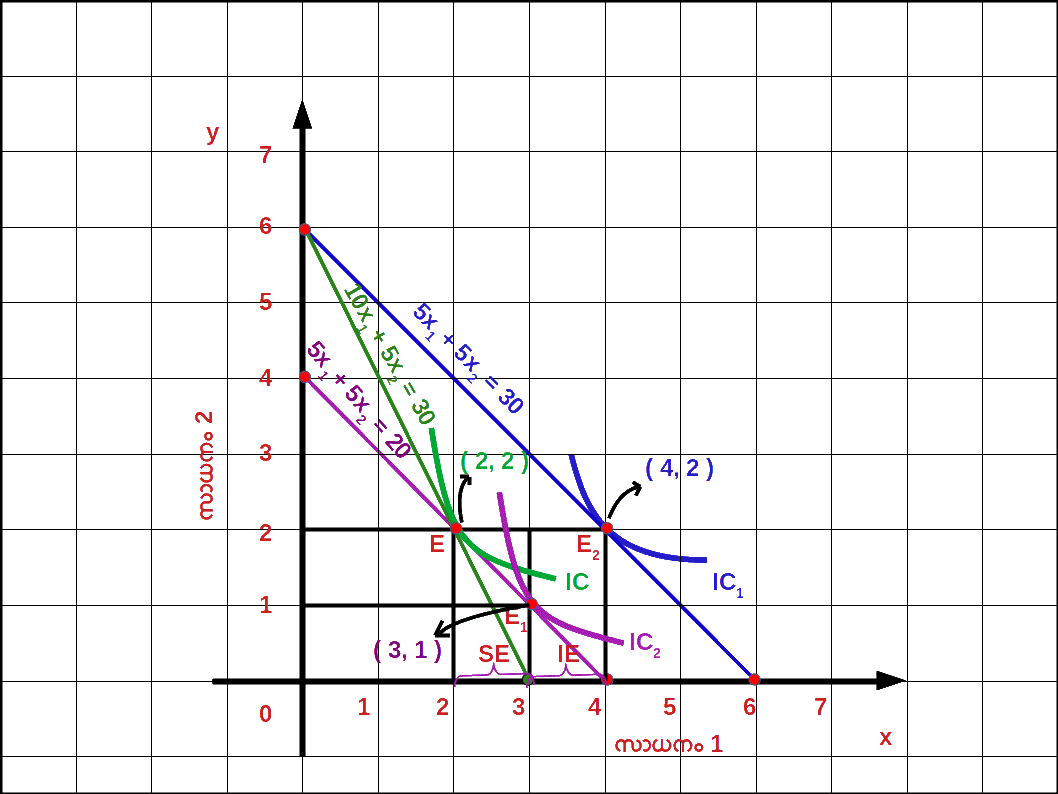
(1). സാധനം 1 ന് സാധനം 2 നെ അപേക്ഷിച്ച് വില കുറയുന്നു. അതായത് , ആപേക്ഷിക വില കുറയുന്നു. ഇത് ഉപഭോക്താവിനെ വില കുറഞ്ഞ സാധനത്തിന്റെ കൂടുതൽ മാത്രകൾ വാങ്ങാൻ പ്രാപ്തനാക്കുന്നു.

( 2 ) ക്രയശേഷി വർധിച്ചതിലൂടെ ഉപഭോക്താവിന്റെ യഥാർത്ഥ വരുമാനം വർധിക്കുന്നു. ഇത് ഉപഭോക്താവിനെ കുറഞ്ഞ സംഖ്യയ്ക്ക് വില കുറവിന് മുമ്പുള്ള അതേ അളവ് സാധനം വാങ്ങാൻ പ്രാപ്തനാക്കുന്നു.
സാധനം 1 ന്റെ വില കുറഞ്ഞതിന്റെ ഫലമായി ബജറ്റ് രേഖ താഴെ ഡയഗ്രം 2.21 ൽ കാണിച്ചിരിക്കുന്നതുപോലെ PL₁ ആയി മാറുന്നു.

Diagram 2.21

PL₁ എന്ന ബജറ്റ് രേഖയിൽ E₁ എന്ന ബിന്ദുവിൽ IC₁ എന്ന നിസംഗതാവക്രം സ്പർശിച്ചിരിക്കുന്നു. E₁ എന്ന ബിന്ദുവിൽ (x^**₁ , x^*₂ ) എന്ന ബണ്ടിൽ സ്വീകരിച്ചുകൊണ്ട് ഉപഭോക്താവ് ഇപ്പോൾ സന്തുലിതാവസ്ഥയിൽ എത്തിയിരിക്കുന്നു. E എന്ന ബണ്ടിലിൽ നിന്ന് (x^*₁ , x^*₂ ) E₁ എന്ന പുതിയ ബണ്ടിലിലേക്കുള്ള മാറ്റത്തെ വില പ്രഭാവം എന്നു പറയുന്നു. സാധനം 1 ന്റെ വില കുറഞ്ഞതുമൂലം ആ സാധനത്തിന്റെ ചോദനത്തിന്റെ അളവ് x*₁ ൽ നിന്ന് x**₁ ആയി വർധിച്ചിരിക്കുന്നു. ഒരു സാധനത്തിന്റെ വിലയിലുള്ള മാറ്റം മൂലം ചോദനത്തിന്റെ അളവിലുള്ള മാറ്റത്തെ വില പ്രഭാവം എന്നു പറയുന്നു. വില പ്രഭാവം പ്രതിസ്ഥാപന പ്രഭാവവും വരുമാന പ്രഭാവവും ചേർന്നതാണ്. വില പ്രഭാവത്തെ പ്രതിസ്ഥാപന പ്രഭാവം , വരുമാന പ്രഭാവം എന്നിങ്ങനെ വേർതിരിക്കാവുന്നതാണ്.
പ്രതിസ്ഥാപന പ്രഭാവവും വരുമാന പ്രഭാവവും വേർതിരിക്കണമെങ്കിൽ വില കുറവുമൂലം യഥാർത്ഥ വരുമാനത്തിലുണ്ടായ നേട്ടം എടുത്തുമാറ്റണം. അതായത് വില പ്രഭാവത്തെ പ്രതിസ്ഥാപന പ്രഭാവം വരുമാന പ്രഭാവം എന്നിങ്ങനെ വേർതിരിക്കണമെങ്കിൽ ഉപഭോക്താവിന്റെ വരുമാനം വില മാറ്റത്തിനു മുമ്പുള്ള ബണ്ടിൽ തെരഞ്ഞെടുക്കാൻ സാധിക്കുന്ന വിധത്തിൽ ചെലവിൽ വ്യത്യാസം വരുത്തണം.
സാധനം 1 ന്റെ വില P₁ ൽ നിന്ന് കണ്ട് കുറയുന്നുവെന്നു കരുതുക. അപ്പോൾ സാധനം 1 ന്റെ പുതിയ വില P₁ – ΔP₁ ആകുന്നു. സാധനം 2 ന്റെ വില മാറാതെ P₂ തന്നെയായി തുടരുന്നു. ഉപഭോ ക്താവിന് (x^*₁ , x^*₂ ) എന്ന ബണ്ടിലിന് വരുന്ന ചെലവ്:

ചെലവ് = ( P₁ – ΔP₁ )x*₁ + P₂x*₂
= P₁x*₁ – ΔP₁ x*₁ + P₂ x*₂
= P₁ x*₁ + P₂ x*₂ – ΔP₁ x*₁
= M – ΔP₁ x*₁
ആയതുകൊണ്ട് ഉപഭോക്താവിന്റെ വരുമാന ത്തിൽ ΔP₁ x*₁ സംഖ്യ കുറവു വരുന്നു . അപ്പോൾ ചെലവിലെ വ്യത്യാസം ΔP₁ x*₁. അതായത് , വില മാറ്റത്തിന് മുമ്പും വിലമാറ്റത്തിന് ശേഷവുമുള്ള ചെലവിലെ വ്യത്യാസം ΔP₁ x*₁ ആണ്. സാധനം 1 ന്റെ വിലയിലുണ്ടായ കുറവുമൂലം യഥാർത്ഥ വരുമാനത്തിലുണ്ടായ നേട്ടം ഇല്ലാതാകാൻ ചെലവ് വ്യത്യാസപ്പെടുത്തുന്നു. ചെലവ് വ്യത്യാസം ( ΔP₁ x*₁ ) ഉപഭോക്താവിന്റെ വരുമാനത്തിൽനിന്ന് കുറയ്ക്കുമ്പോൾ ( M – ΔP₁ x*₁ ) ഡയഗ്രം 2.22 ൽ കാണിച്ചിരിക്കുന്നതുപോലെ ബജറ്റ് രേഖ P’L’ ആയിമാറുന്നു. P’L’ എന്ന ബജറ്റ് രേഖ E എന്ന ബണ്ടിലിലൂടെ PL₁ എന്ന ബജറ്റ് രേഖയ്ക്ക് സമാന്തരമായി ഇടത്തേക്ക് മാറുന്നു.

Diagram 2.22

ഇപ്പോൾ ഉപഭോക്താവ് തന്റെ വരുമാനം മുമ്പുണ്ടായിരുന്ന ക്രയശേഷിക്ക് തുല്യമായി ക്രമീകരിച്ചിരിക്കുന്നു. E എന്ന ബിന്ദുവിൽ നിന്ന് E₂ എന്ന ബിന്ദുവിലേക്കുള്ള മാറ്റത്തെ പ്രതിസ്ഥാപന പ്രഭാവം എന്നു പറയുന്നു. E₂ എന്ന ബിന്ദുവിൽ സാധനം 2 ന്റെ ചോദനത്തിന്റെ അളവ് x*₂ ൽ നിന്ന് x’₂ ആയി കുറച്ചുകൊണ്ട് സാധനം 1 ന്റെ അളവ് x*₁ ൽ നിന്ന് x’₁ ആയി വർധിച്ചിരിക്കുന്നു. ( x^*₁ , x^*₂ ) എന്ന ബണ്ടിലിനു പകരം ( x^‘₁ , x^‘₂ ) എന്ന ബണ്ടിൽ പ്രതിസ്ഥാപനം ചെയ്യുന്നു. വില കുറഞ്ഞ സാധനത്തിന്റെ കൂടുതൽ അളവ് വിലയിൽ മാറ്റം വരാത്ത സാധനത്തിന് പകരം ചോദനം ചെയ്യുന്നു. ഇതിനെയാണ് പ്രതിസ്ഥാപന പ്രഭാവം എന്നു പറയുന്നത്.
E₂ എന്ന ബിന്ദുവിൽനിന്ന് E₁ എന്ന ബിന്ദുവിലേക്കുള്ള മാറ്റത്തെ വരുമാന പ്രഭാവം എന്ന് പറയുന്നു.(x^‘₁ , x^‘₂ ) എന്ന ബണ്ടിലിൽ നിന്ന് ( x^**₁ , x^*₂ ) എന്ന ബണ്ടിലിലേക്ക് മാറുന്നു. സാധനം 1 ന്റെ വിലയിൽ മാറ്റം വരുമ്പോൾ , തൽഫലമായി ഉണ്ടാകുന്ന ക്രയശേഷിയിലെ മാറ്റം മൂലം ചോദനത്തിന്റെ അളവിലുണ്ടാകുന്ന മാറ്റത്തെ വരുമാന പ്രഭാവം എന്നു പറയുന്നു.
മൊത്തം പ്രഭാവം E യിൽ നിന്ന് E₁ ലേക്കുള്ള മാറ്റമാണ്. ഇത് പ്രതിസ്ഥാപന പ്രഭാവവും വരുമാന പ്രഭാവവും ചേർന്നതാണ്. PE = SE + IE അതുകൊണ്ട് ഈ രണ്ട് പ്രഭാവവും ചോദനത്തിന്റെ അളവും അതിന്റെ വിലയും തമ്മിൽ വിപരീത ബന്ധത്തിന് കാരണമാകുന്നു.
EXAMPLE 2.13 : ഒരു ഉപഭോക്താവിന്റെ വരുമാനം 30 രൂപയാണെന്ന് സങ്കല്പിക്കുക. സാധനം 1 ന്റെ വില 10 യും സാധനം 2 ന്റെ വില 15 യുമാ ണെന്നും ഉപഭോക്താവിന്റെ ഏറ്റവും അനുകൂലമായ ബണ്ടിൽ ( 2 2 ) ആണെന്നും കരുതുക. ഗ്രാഫ് 2.23 ൽ 10x₁ + 5x₂ = 30 എന്ന ബജറ്റ് രേഖയിൽ ഏറ്റവും അനുകൂലമായ ( 2 , 2 ) എന്ന ബണ്ടിലും രേഖപ്പെടുത്തിയിരിക്കുന്നു.
ഇനി സാധനം 1 ന്റെ വില 10 യിൽ നിന്നും 5 യായി കുറയുന്നുവെന്നു കരുതുക. ആപേക്ഷിക വില കുറയുന്നു. അപ്പോൾ ബജറ്റ് രേഖ 5x₁ + 5x₂ = 30 എന്നാകുന്നു. ഇപ്പോൾ ഉപഭോക്താവിന് ഏറ്റവും അനുകൂലമായ ബണ്ടിൽ ( 4 , 2 ) ആണ്. ( 2 , 2 ) എന്ന ബണ്ടിലിൽ നിന്ന് ( 4 , 2 ) എന്ന ബണ്ടിലിലേക്കുള്ള മാറ്റത്തെ വില പ്രഭാവമെന്നു പറയുന്നു. അതായത് സാധനം 1 ന്റെ വില കുറഞ്ഞതുമൂലം ആ സാധനം ഇപ്പോൾ 2 യൂണിറ്റിന് പകരം 4 യൂണിറ്റ് വാങ്ങുന്നു. മാത്രമല്ല വില കുറഞ്ഞതിന്റെ ഫലമായി ആദ്യം മേടിച്ച ( 2 , 2 ) എന്ന ബണ്ടിൽ ഇപ്പോൾ ഉപഭോക്താവിന് 20 യ്ക്ക് വാങ്ങാൻ കഴിയുന്നു. ഇത് വരുമാന പ്രഭാവം. ( 5 × 2 + 5 × 2 = 10 + 10 = 20 ) ഉപഭോക്താവിന്റെ വരുമാനം 10 കണ്ട് ( 30 – 20 = 10 ) കുറയുകയാണെങ്കിൽ , അയാൾക്ക് ( 2 , 2 ) എന്ന ബണ്ടിൽ കഷ്ടിച്ച് വാങ്ങിക്കാൻ കഴിയും. അപ്പോൾ ബജറ്റ് രേഖ 5x₁ + 5x₂ = 20 എന്നാകും . ഈ ബജറ്റ് രേഖ ഇടതുഭാഗത്തേക്ക് 5x₁ + 5x₂ = 30 എന്ന ബജറ്റ് രേഖയ്ക്ക് സമാന്തരമായി മാറുന്നു. ഇപ്പോൾ ഉപഭോക്താവിന് 10 അധിക വരുമാനമുണ്ട്. ഈ സംഖ്യകൊണ്ട് അയാൾക്ക് ആവശ്യമെങ്കിൽ കൂടുതൽ അളവ് സാധനം വാങ്ങാം. സാധനം 1 ആണ് കൂടുതൽ വാങ്ങാൻ ഉദ്ദേശിക്കുന്ന തെങ്കിൽ അയാൾക്ക് 5x₁ = 10 , x₁ = 10 / 5 = 2 യൂണിറ്റ് വാങ്ങാം. സാധനം 2 ആണ് കൂടുതൽ വാങ്ങാൻ ഉദ്ദേശിക്കുന്നതെങ്കിൽ അയാൾക്ക് 5x₂ = 10 , x₁ 10 / 5 = 2 യൂണിറ്റ് വാങ്ങാം. അല്ലെങ്കിൽ അയാൾക്ക് സാധനം 1 ന്റെയും സാധനം 2 ന്റെയും ഓരോ യൂണിറ്റ് വീതം വാങ്ങാൻ കഴിയും.

Diagram 2.23

അപ്പോൾ പ്രതിസ്ഥാപന പ്രഭാവവും വരുമാന പ്രഭാവവും മൂലം സാധനത്തിന്റെ വില കുറയുമ്പോൾ അതിന്റെ ചോദനം വർധിക്കുന്നു. അതുകൊണ്ടാണ് ചോദന വക്രം നെഗറ്റീവ് ചെരിവായിരിക്കുന്നത്.
സാധനം 1 ന്റെ അളവ് 2 യൂണിറ്റിൽനിന്ന് 4 യൂണിറ്റായി കൂടുന്നത് വില പ്രഭാവവും , സാധനം 1 ന്റെ അളവ് 2 യൂണിറ്റിൽ നിന്ന് 3 യൂണിറ്റാകുന്നത് പ്രതിസ്ഥാപന പ്രഭാവവുമാണ്. സാധനം 1 ന്റെ അളവ് 2 യൂണിറ്റിൽ നിന്ന് 4 യൂണിറ്റാകുന്നതാണ് വരുമാന പ്രഭാവം.

രേഖീയ ചോദനം ( Linear Demand )
ചോദനവും വിലയും തമ്മിലുള്ള ബന്ധം രേഖീയമോ രേഖീയമല്ലാത്തതോ ആവാം. ബീജ ഗണിത രൂപത്തിൽ ഒരു രേഖീയ ചോദന വക്രം താഴെ കൊടുത്ത രൂപത്തിലെഴുതാം ;

q = a – bP; 0 ≤ P ≤ $ \mathbf {\frac{a}{b}} $ ആണ്.
= 0 ; P > $ \mathbf {\frac{a}{b}} $ ആണെങ്കിൽ.

ഈ രേഖീയ ചോദന സമവാക്യത്തിൽ ലംബഛേദവും , – b ചോദനവക്രത്തിന്റെ ചെരിവും , P സാധനത്തിന്റെ വിലയും , q ചോദന ത്തിന്റെ അളവുമാണ്. കൂടാതെ വില പൂജ്യമായാൽ ചോദനം a യും , വില $ \mathbf {\frac{a}{b}} $ ആയാൽ ചോദനം പൂജ്യവുമാണ്.

Diagram 2.24

ഡയഗ്രം 2.24 ൽ രേഖീയ ചോദന വക്രം വരച്ചിരിക്കുന്നു. വില മാറുന്നതിനനുസരിച്ച് ചോദനത്തിലുണ്ടാകുന്ന മാറ്റത്തിന്റെ നിരക്കാണ് ചോദന വക്രത്തിന്റെ ചെരിവ് സൂചിപ്പിക്കുന്നത്. അതായത് വിലയിൽ ഓരോ യൂണിറ്റ് മാറ്റമുണ്ടാകുമ്പോഴും ചോദനം -b യൂണിറ്റ് വീതം മാറും. b യുടെ ചിഹ്നം നെഗറ്റീവായതുകൊണ്ട് വിലയും ചോദനവും തമ്മിലുള്ള ബന്ധം വിപരീതമാണ്. വില 1 യൂണിറ്റ് കൂടിയാൽ ചോദനം b യൂണിറ്റ് കുറയും. ( ചോദന വക്രത്തിന്റെ ചെരിവ് $ \mathbf {\frac{Δq}{ΔP}} $ യാണ് .)
EXAMPLE 2.14 : q = a – bP എന്ന ചോദന നിയമ സമവാക്യത്തിൽ a യ്ക്കും b യ്ക്കും മൂല്യങ്ങൾ നല്കി ചോദന വക്രം ( രേഖ ) വരയ്ക്കാം. a യുടെ മൂല്യം 10 എന്നും b യുടെ മൂല്യം 2 എന്നും കരുതുക. അപ്പോൾ , q = 10 – 2P എന്ന ചോദന സമവാക്യം ലഭിക്കുന്നു. ഇവിടെ 0 ≤ P ≤ 5 ആണ്. P > 5 ആണെങ്കിൽ ചോദനം പൂജ്യമായിരിക്കും.
ഇവിടെ P = 0 ആകുമ്പോൾ , q = 10 ആയിരിക്കും , i.e. , q = 10 – 2 × 0 = 10 – 0 = 10. ഇത് ഹൊറിസോണ്ടൽ ഇന്റര്സെപ്റ്റും ചോദനം പൂജ്യമായാൽ വില 5 ആയിരിക്കും.

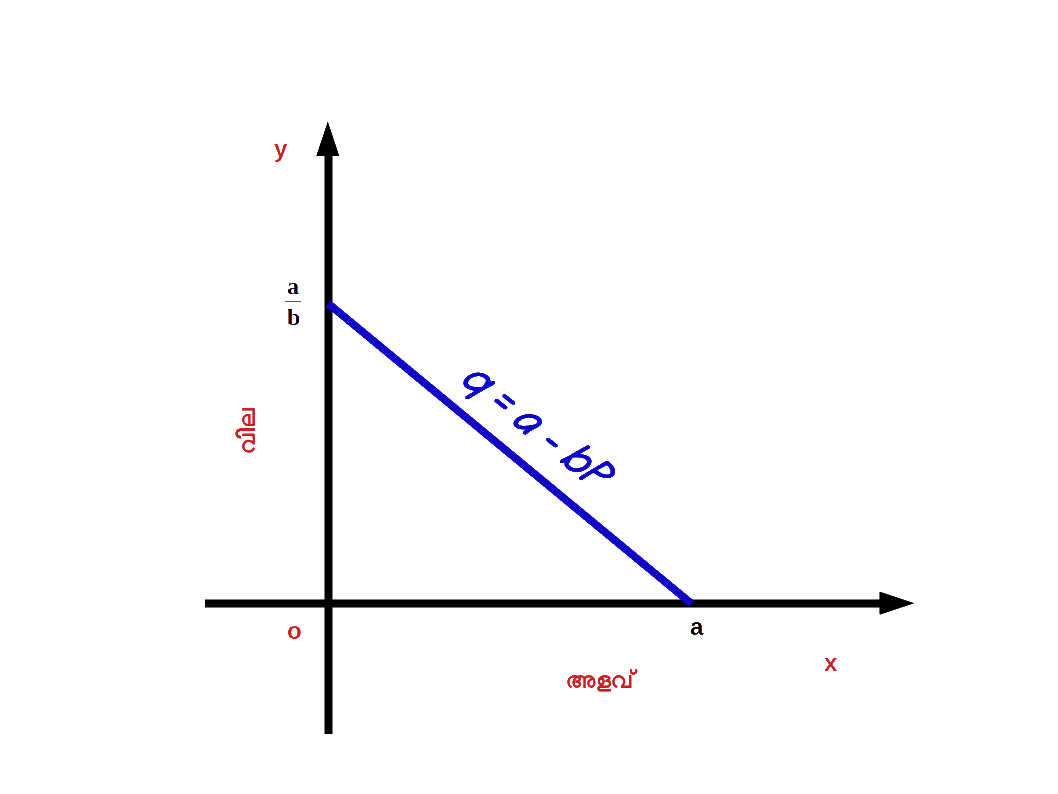
0 = 10 – 2P (q = 0)
2P = 10
P = ${\frac{10}{2}}$ = 5

ഇത് വെർട്ടിക്കൽ ഇന്റർസെപ്റ്റുമാണ്. രേഖീയ ചോദന വക്രം ഗ്രാഫ് 2.25 ൽ വരച്ചിരിക്കുന്നു.

Diagram 2.25

q = 10 – 2P എന്ന ഗണിത ചോദന നിയമ സമവാക്യം ഉപയോഗിച്ചുകൊണ്ട് വില 0 മുതൽ 5 വരെ വരുമ്പോൾ ചോദനത്തിന്റെ വ്യത്യസ്ത അളവ് പട്ടിക 2.5 ൽ കൊടുത്തിരിക്കുന്നു.

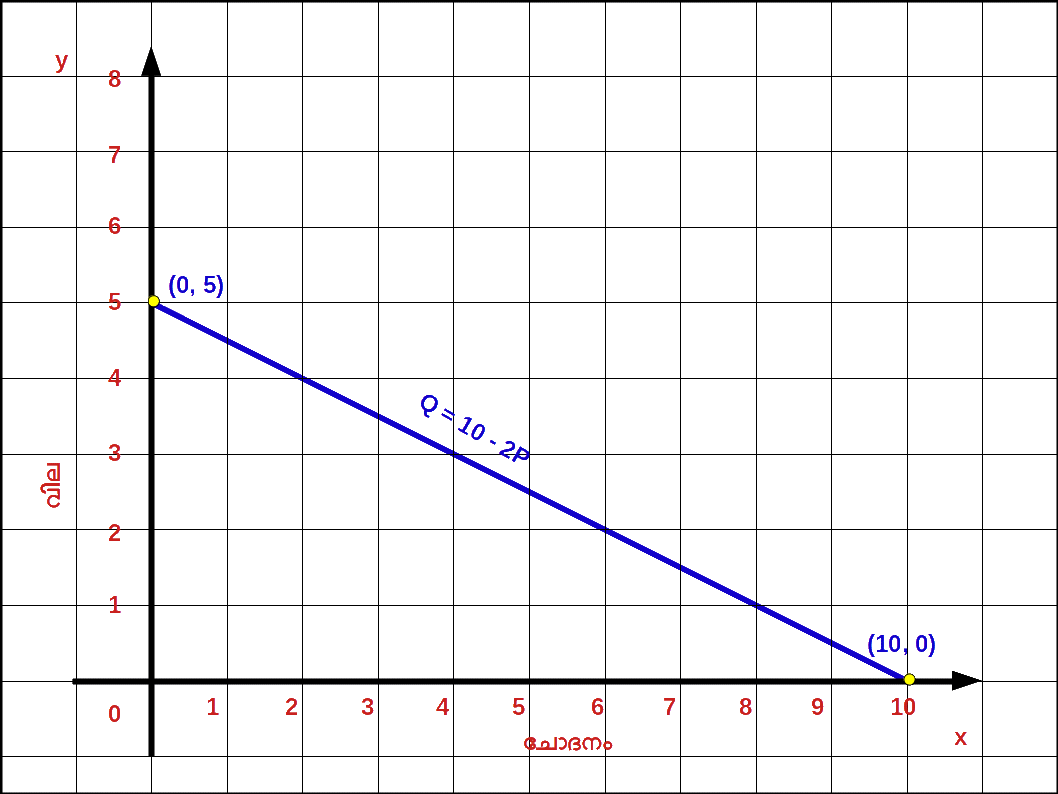
Table 2.5

വില (P) ചോദനം (q) കാണുന്ന രീതി. q = 10 – 2P

0 10 q = 10 – 2 × 0 = 10 – 0 = 10

1 8 q = 10 – 2 × 1 = 10 – 2 = 8

2 6 q = 10 – 2 × 2 = 10 – 4 = 6

3 4 q = 10 – 2 × 3 = 10 – 6 = 4

4 2 q = 10 – 2 × 4 = 10 – 8 = 2

5 0 q = 10 – 2 × 5 = 10 – 10 = 0

ഒരു വ്യക്തിയുടെ ചോദനവും വിലയും തമ്മിലുള്ള ബന്ധം കാണിക്കുന്ന പട്ടികയെ വ്യക്തിഗത ചോദന പട്ടിക ( individual demand schedule ) എന്നു പറയുന്നു.

ഒരു സാധനത്തിന്റെ ചോദനത്തെ നിർണ്ണയിക്കുന്ന ഘടകങ്ങൾ
പരമ്പരാഗത ചോദന സിദ്ധാന്ത പ്രകാരം ഒരു വസ്തുവിന്റെ ചോദനത്തെ നിർണ്ണയിക്കുന്നത് പ്രധാനമായും നാല് ഘടകങ്ങളാണ്. അവ :

( 1 ) സാധനത്തിന്റെ വില : ചോദനത്തെ നിർണ്ണയിക്കുന്ന ഏറ്റവും പ്രധാന ഘടകം ആ സാധനത്തിന്റെ വിലയാണ് ഒരു സാധനത്തിന്റെ വിലയും ചോദനവും തമ്മിൽ വിപരീത ബന്ധമാണെന്ന് ചോദന നിയമം വ്യക്തമാക്കുന്നു.

( 2 ) ഉപഭോക്താവിന്റെ വരുമാനം : ചോദനത്ത നിർണ്ണയിക്കുന്ന മറ്റൊരു ഘടകമാണ് ഉപഭോ ക്താവിന്റെ വരുമാനം . വരുമാനവും ചോദനവും തമ്മിലുള്ള ബന്ധം സാധനത്തിന്റെ സ്വഭാവം അനുസരിച്ചായിരിക്കും . വരുമാനത്തിന്റെ അടിസ്ഥാനത്തിൽ സാധനങ്ങളെ സാധാരണ സാധനങ്ങൾ , തരംതാണ സാധനങ്ങൾ എന്ന് തരം തിരിക്കാം.

( a ) സാധാരണ സാധനങ്ങൾ ( Normal goods ) : ഉപഭോക്താവിന്റെ വരുമാനം വർധിക്കുമ്പോൾ സാധനത്തിന്റെ ചോ ദനം വർധിക്കുകയും വരുമാനം കുറയുമ്പോൾ ചോദനം കുറയുകയും ചെയ്യുന്ന വസ്തുക്കളെ സാധാരണ സാധനങ്ങൾ എന്നു പറയുന്നു.
EXAMPLE 2.15 : ടി.വി. കംപ്യൂട്ടർ , നല്ല വസ്ത്രങ്ങൾ തുടങ്ങിയവ. ഒരു വ്യക്തിക്ക് സാധാരണ സാധനങ്ങൾ എന്നു കരുതുന്നവ മറ്റൊരു വ്യക്തിക്ക് സാധാരണ സാധനമായിക്കൊള്ളണമെന്നില്ല. ഉപഭോക്താവിന്റെ വരുമാനവും സാധാരണ സാധനങ്ങൾക്കുള്ള ചോദനവും തമ്മിലുള്ള ബന്ധം പോസിറ്റീവാണ്. അതായത് , ഉപഭോക്താവിന്റെ വരുമാനവും സാധാരണ സാധനങ്ങൾക്കുള്ള ചോദനവും ഒരേ ദിശയിൽ മാറുന്നു.

( b ) തരം താണ സാധനങ്ങൾ ( Inferior goods ) : ഉപഭോക്താവിന്റെ വരുമാനം വർധിക്കുമ്പോൾ ചോദനം കുറയുകയും വരുമാനം കുറയുമ്പോൾ ചോദനം വർധിക്കുകയും ചെയ്യുന്ന വസ്തുക്കളെ തരംതാണ വസ്തുക്കൾ എന്നു പറയുന്നു. ഇത്തരം വസ്തുക്കൾക്കുള്ള ചോദനവും ഉപഭോക്താവിന്റെ വരുമാനവും തമ്മിലുള്ള ബന്ധം വിപരീതമാണ് .
EXAMPLE 2.16 മണ്ണെണ്ണ, ഗ്യാസ് സ്റ്റൗവിനെക്കാൾ തരംതാണതാണ്. ഓർഡിനറി ബസിൽ യാത്ര ചെയ്യുന്നത് കാറിൽ യാത്ര ചെയ്യുന്നതിനെക്കാൾ തരംതാണതാണ്. കൂടാതെ ഗുണനിലവാരം കുറഞ്ഞ മറ്റ് ഭക്ഷ്യധാന്യങ്ങൾ , ബജ്റ അരിയേക്കാൾ തരംതാണതാണ്.

( 3 ) മറ്റ് ബന്ധപ്പെട്ട സാധനങ്ങളുടെ വില : ഒരു സാധനത്തിന്റെ ചോദനത്തെ നിർണ്ണയിക്കുന്ന മറ്റൊരു ഘടകമാണ് ആ സാധനവുമായി ബന്ധപ്പെട്ട സാധനങ്ങളുടെ വില. അത്തരം സാധനത്തിന്റെ വിലയും ചോദനവും തമ്മിലുള്ള ബന്ധത്തിന്റെ അടിസ്ഥാനത്തിൽ വസ്തുക്കളെ പ്രതിസ്ഥാപന വസ്തുക്കളെന്നും പൂരകവസ്തുക്കളെന്നും തരംതിരിച്ചിരിക്കുന്നു.

( a ) പ്രതിസ്ഥാപന വസ്തുക്കൾ : ഒരാവശ്യത്തെ തൃപ്തിപ്പെടുത്തുവാൻ വേണ്ടി ഒരു സാധനത്തിനു പകരം ഉപയോഗിക്കാൻ പറ്റുന്ന മറ്റ് സാധനങ്ങളാണ് പ്രതിസ്ഥാപന വസ്തുക്കൾ.
EXAMPLE 2.17 ചായയും കാപ്പിയും , ബസും തീവണ്ടിയും , കാറും ജീപ്പും , ഷൂവും ചെരിപ്പും. പ്രതിസ്ഥാപന വസ്തുക്കളുടെ വിലയും ചോദനവും തമ്മിൽ പോസിറ്റീവ് ബന്ധമാണ്. രണ്ട് പ്രതിസ്ഥാപന വസ്തുക്കളിൽ ഒന്നിന്റെ വില മാറുന്ന അതേ ദിശയിൽ മറ്റേ സാധനത്തിന്റെ ചോദനവും മാറും. ചായയുടെ വില വർധിക്കുമ്പോൾ കാപ്പിയുടെ ചോദനം വർധിക്കുകയും , ചായയുടെ വില കുറയുമ്പോൾ കാപ്പിയുടെ ചോദനം കുറയുകയും ചെയ്യുന്നു.

( b ) പൂരക വസ്തുക്കൾ ( Complementary goods ) : ഒരാവശ്യത്തെ തൃപ്തിപ്പെടുത്താൻ ഒന്നിലധികം സാധനങ്ങൾ ആവശ്യമെങ്കിൽ അത്തരം സാധനങ്ങളെ പൂരക വസ്തുക്കളെന്നു പറയുന്നു.
EXAMPLE 2.18 : പേനയും മഷിയും , കാറും പെട്രോളും ( ഡീസൽ ) , താഴും താക്കോലും , ഷൂവും സോക്‌സും. പൂരകവസ്തുക്കളുടെ ചോദനവും വിലയും വിപരീത ബന്ധമാണ്. ഇവ തമ്മിൽ എതിർ ദിശയിൽ മാറുന്നു. അതായത് , പൂരക വസ്തുക്കളിൽ ഒന്നിന്റെ വില വർധിക്കുമ്പോൾ മറ്റേ സാധനത്തിന്റെ ചോദനം കുറയുകയും വില കുറയുമ്പോൾ ചോദനം കൂടുകയും ചെയ്യുന്നു.

( 4 ) ഉപഭോക്താവിന്റെ അഭിരുചിയും താല്പര്യങ്ങളും : ചോദനത്തെ നിർണ്ണയിക്കുന്ന മറ്റൊരു ഘടകം ഉപഭോക്താവിന്റെ അഭിരുചിയും ഇഷ്ടാനിഷ്ടങ്ങളുമാണ്. ഒരു സാധനത്തോടുള്ള ഉപഭോക്താവിന്റെ താല്പര്യം വർധിക്കുമ്പോൾ ആ സാധനത്തിന്റെ ചോദനം വർധിക്കുകയും അവയോടുള്ള ഇഷ്ടം കുറയുമ്പോൾ അതിന്റെ ചോദനം കുറയുകയും ചെയ്യുന്നു.

ചോദനത്തിലെ മാറ്റങ്ങൾ ( Changes in Demand )
ചോദനത്തിലെ മാറ്റങ്ങളെ പൊതുവേ രണ്ടായി തരംതിരിക്കാം. അവ:

1. ചോദന വക്രത്തിലൂടെയുള്ള മാറ്റം

2. ചോദന വക്രത്തിന്റെ മാറ്റം അഥവാ ചാട്ടം

ഇവയോരോന്നും പൂരുക്കി വിവരിക്കാം.

1. ചോദന വക്രത്തിലൂടെയുള്ള മാറ്റം ( Movement along the demand curve ) :
വിലയിലുള്ള മാറ്റത്തിന്റെ ഫലമായി ചോദനത്തിലുണ്ടാകുന്ന മാറ്റത്തെയാണ് ചോദനത്തിലൂടെയുള്ള മാറ്റം എന്നു പറയുന്നത്. ചോദന വക്രത്തിലൂടെയുള്ള മാറ്റത്തിന് കാരണം സാധനത്തിന്റെ വിലയിലുള്ള മാറ്റമാണ്. ഉപഭോക്താവിന്റെ വരുമാനം , ബന്ധപ്പെട്ട സാധനങ്ങളുടെ വില , ഉപഭോക്താവിന്റെ താല്പര്യങ്ങളും ഇഷ്ടങ്ങളും തുടങ്ങിയ വിലയിതരഘടകങ്ങളിൽ യാതൊരു മാറ്റവും സംഭവിക്കുന്നില്ല. ചോദന വക്രത്തിലൂടെയുള്ള മാറ്റം രണ്ട് തരത്തിലുണ്ട്. അവ :

( a ) ചോദനത്തിന്റെ വികാസം

( b ) ചോദനത്തിന്റെ സങ്കോചം

( a ) ചോദനത്തിന്റെ വികാസം ( Expansion of demand ) : വില കുറഞ്ഞതിന്റെ ഫലമായി ചോദന വക്രത്തിലൂടെ താഴേക്ക് നീങ്ങുന്നതിനെയാണ് ചോദനത്തിന്റെ വികാസം എന്നു പറയുന്നത്. സാധനത്തിന്റെ വില കുറയുന്നതുമൂലം ചോദനത്തിന്റെ അളവിലുണ്ടാകുന്ന വർധനവിന് ചോദനത്തിന്റെ വികാസം എന്നു പറയുന്നു. ഡയഗ്രം 2.26 ൽ സാധനത്തിന്റെ വില P ൽ നിന്ന് P₁ ആയി കുറഞ്ഞപ്പോൾ ചോദനത്തിന്റെ അളവ് q ൽ നിന്ന് q₁ ആയി വർധിച്ചിരിക്കുന്നു. DD എന്ന ചോദന വക്രത്തിലെ a എന്ന ബിന്ദുവിൽ നിന്ന് b എന്ന ബിന്ദുവിലേക്ക് താഴേക്ക് നീങ്ങിയിരിക്കുന്നു. a ൽനിന്ന് b യിലേക്കുള്ള മാറ്റത്തെയാണ് ചോദനത്തിന്റെ വികാസം എന്നു പറയുന്നത്.

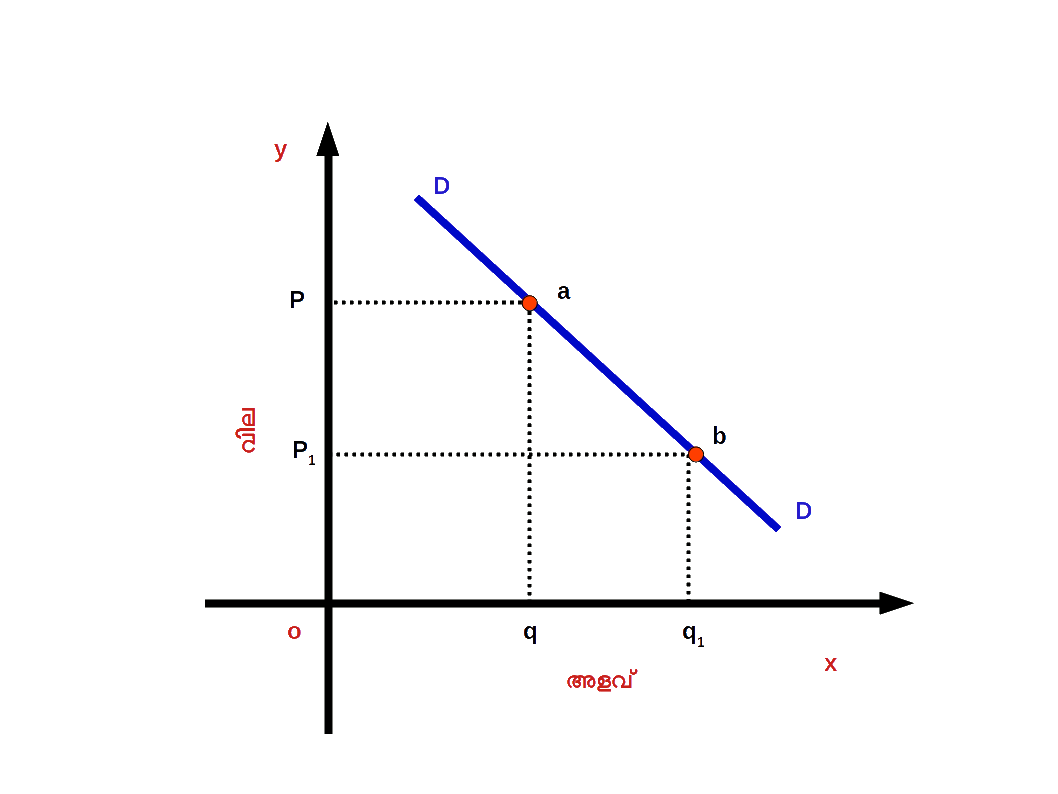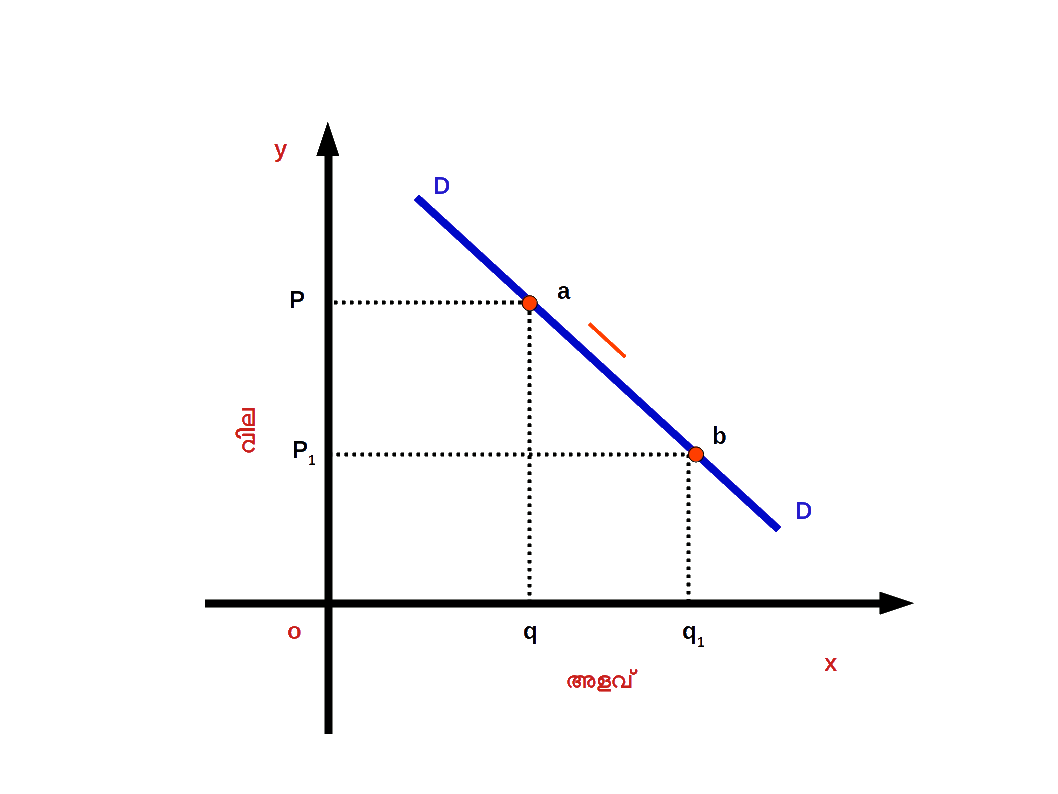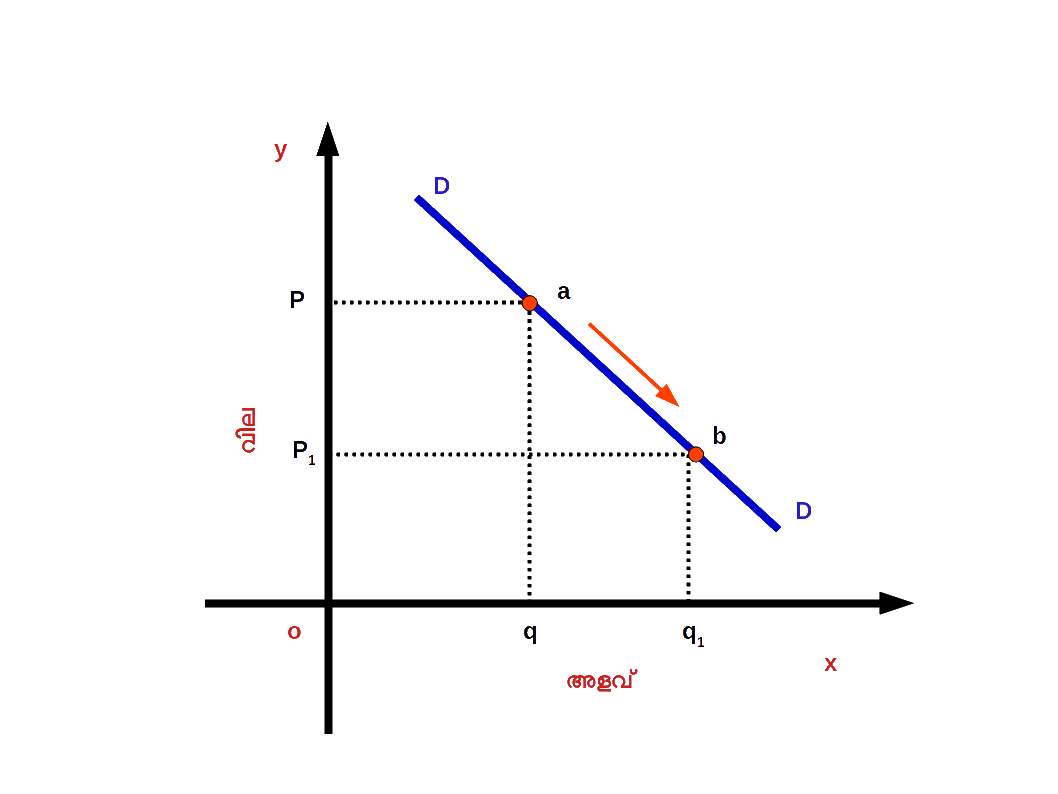Diagram 2.26

( b ) ചോദനത്തിന്റെ സങ്കോചം ( Contraction of demand ) : വില വർധനവിന്റെ ഫലമായി ചോദന വക്രത്തിലൂടെ മുകളിലേക്ക് നീങ്ങുന്നതിനെയാണ് ചോദനത്തിന്റെ സങ്കോചം എന്നു പറയുന്നത്. മറ്റൊരു വിധത്തിൽ പറഞ്ഞാൽ , സാധനത്തിന്റെ വില വർധിക്കുന്നതുമൂലം ചോദനത്തിന്റെ അളവിലുണ്ടാകുന്ന കുറവിന് ചോദനത്തിന്റെ സങ്കോചം എന്നു പറയുന്നു. 2.27 ൽ സാധനത്തിന്റെ വില P₁ൽ നിന്ന് P ആയി വർധിച്ചപ്പോൾ ചോദനത്തിന്റെ അളവ് q₁ ൽ നിന്ന് q ആയി കുറഞ്ഞിരിക്കുന്നു. DD എന്ന ചോദന വക്രത്തിലെ b എന്ന ബിന്ദുവിൽ നിന്ന് a എന്ന മുകളിലെ ബിന്ദുവിലേക്കു നീങ്ങിയിരിക്കുന്നു. b യിൽ നിന്ന് a യിലേക്കുള്ള മാറ്റത്തെയാണ് ചോദനത്തിന്റെ സങ്കോചം എന്നു പറയുന്നത്.

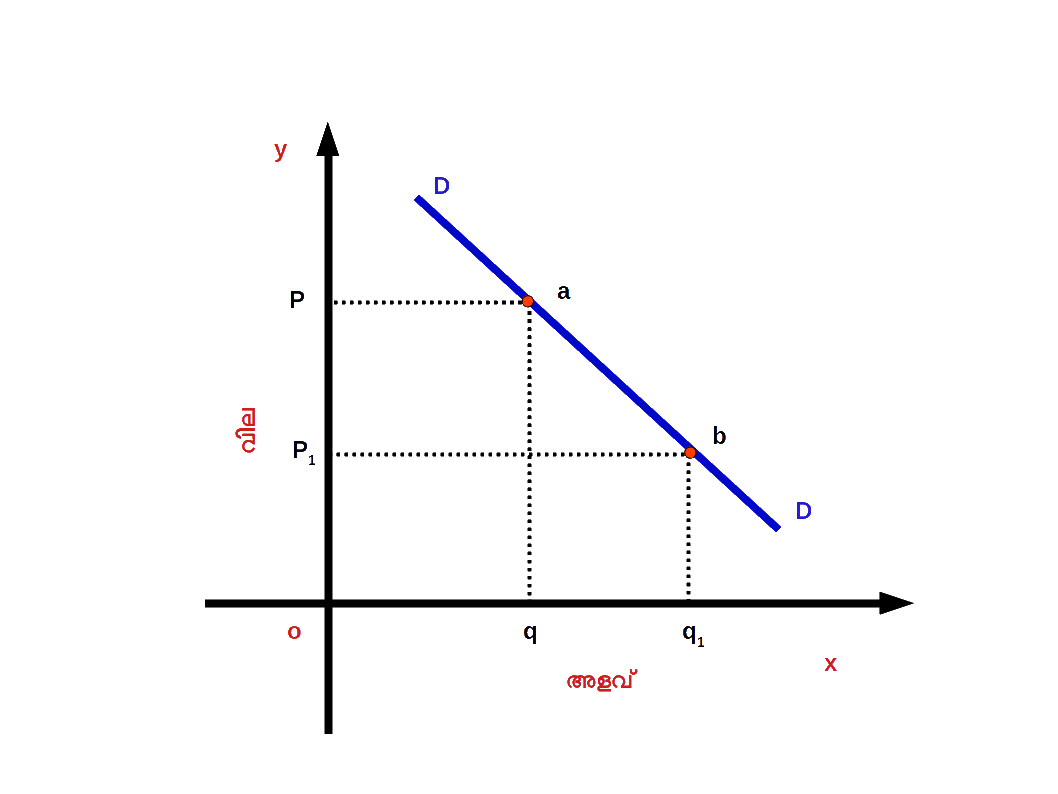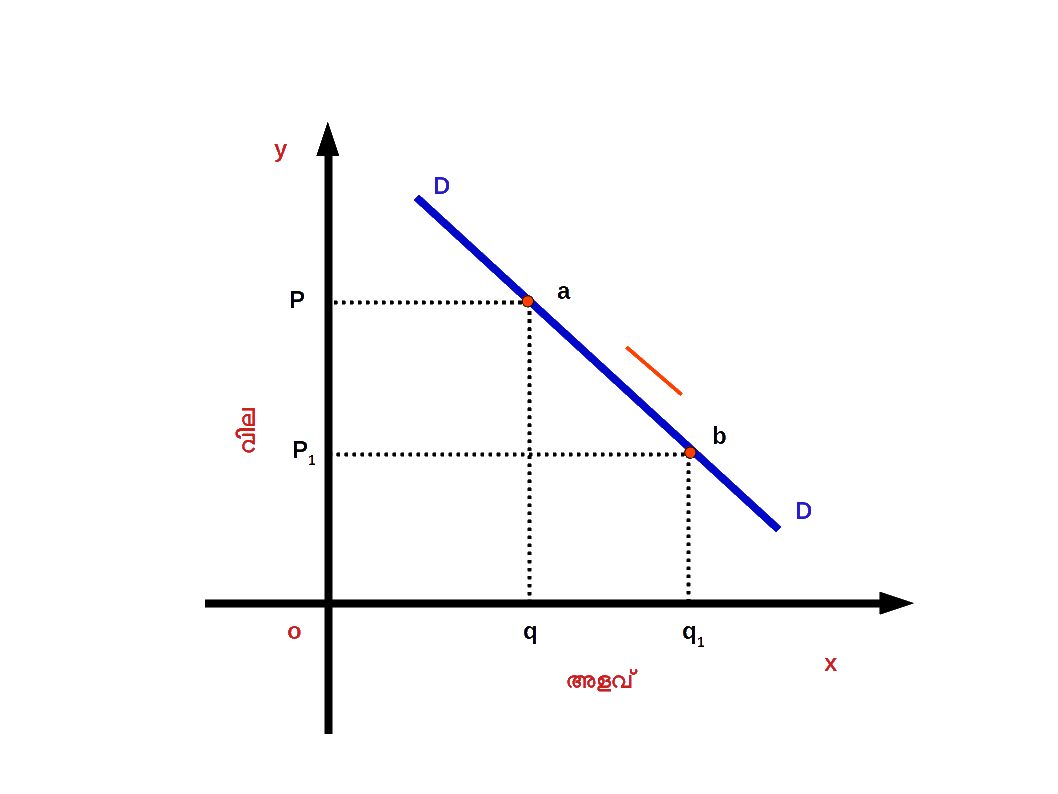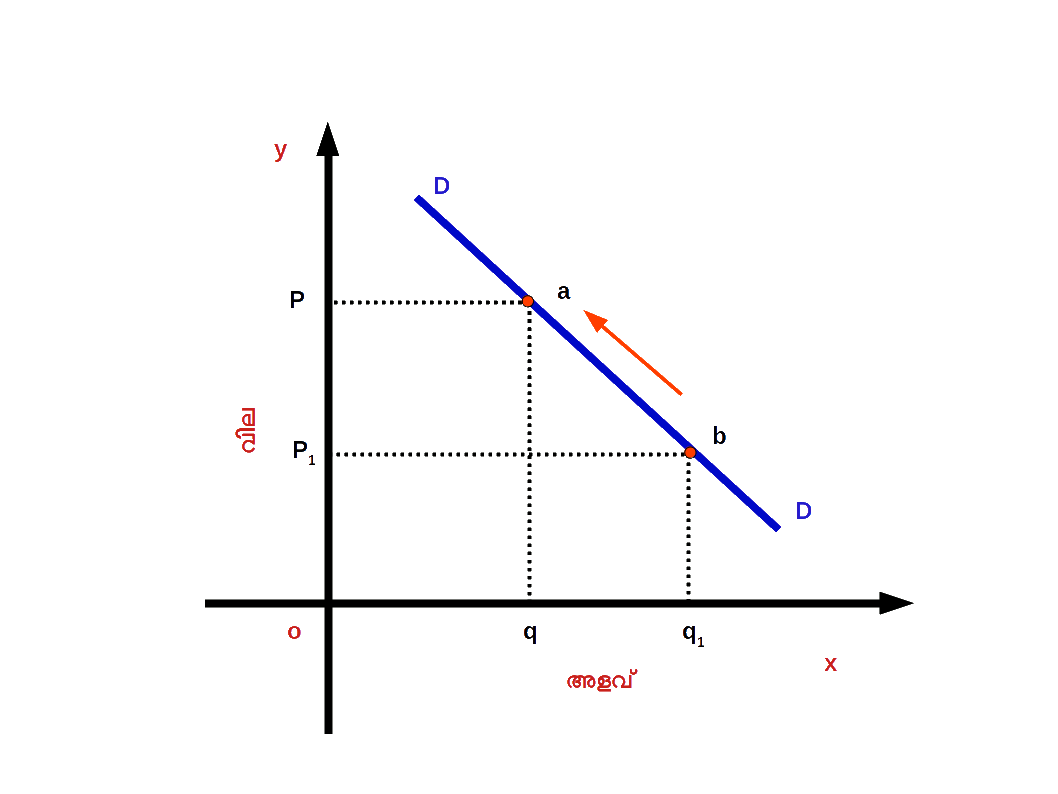Diagram 2.27

2. ചോദന വക്രത്തിന്റെ മാറ്റം ( Shift of demand curve ) :
വിലയൊഴിച്ചുള്ള മറ്റ് ഘടകങ്ങളിലെ മാറ്റങ്ങൾ മൂലം ഒരു സാധനത്തിന്റെ ചോദനത്തിന്റെ അളവിലുണ്ടാകുന്ന മാറ്റത്തെ ചോദന വക്രത്തിന്റെ മാറ്റം എന്നു പറയുന്നു . ചോദന വക്രത്തിന്റെ മാറ്റത്തിന് കാരണം വിലയിതര ഘടകങ്ങളിലുള്ള മാറ്റമാണ്. ചോദന വക്രത്തിന്റെ മാറ്റം രണ്ട് തരത്തിലുണ്ട് . അവ :

( a ) ചോദന വർധനവ്

( b ) ചോദന കുറവ്

( a ) ചോദന വർധനവ് ( Increase in demand ) : വിലയിതര ഘടകങ്ങളിൽ അനുകൂലമായ മാറ്റത്തിന്റെ ഫലമായി ചോദന വക്രം വലത് ഭാഗത്തേക്ക് മാറുന്നതിനെയാണ് ചോദന വർധനവ് എന്നു പറയുന്നത്. ഡയഗം 2.28 ൽ DD എന്നത് ആദ്യത്തെ ചോദന വക്രമാണ് . OP വിലയ്ക്ക് Oq സാധനം ചോദനം ചെയ്യുന്നു. വിലയിതര ഘടകങ്ങളിൽ അനുകുലമായ മാറ്റമുണ്ടായതിന്റെ ഫലമായി DD എന്ന ചോദന വക്രം D₁D₁ എന്ന പുതിയ ചോദന വക്രമായി വലതുഭാഗത്തേക്ക് ചാടുന്നു. അഥവാ മാറുന്നു. അപ്പോൾ ചോദനം Oq ൽ നിന്ന് Oq₁ ആയി വർധിക്കുന്നു. വില OP യായി തുടരുന്നു ( മാറ്റമില്ല ). DD എന്ന ചോദന D₁D₁ ആയി വലതുഭാഗത്തേക്കുള്ള മാറ്റത്തെയാണ് ചോദന വർധനവ് എന്നു പറയുന്നത്.

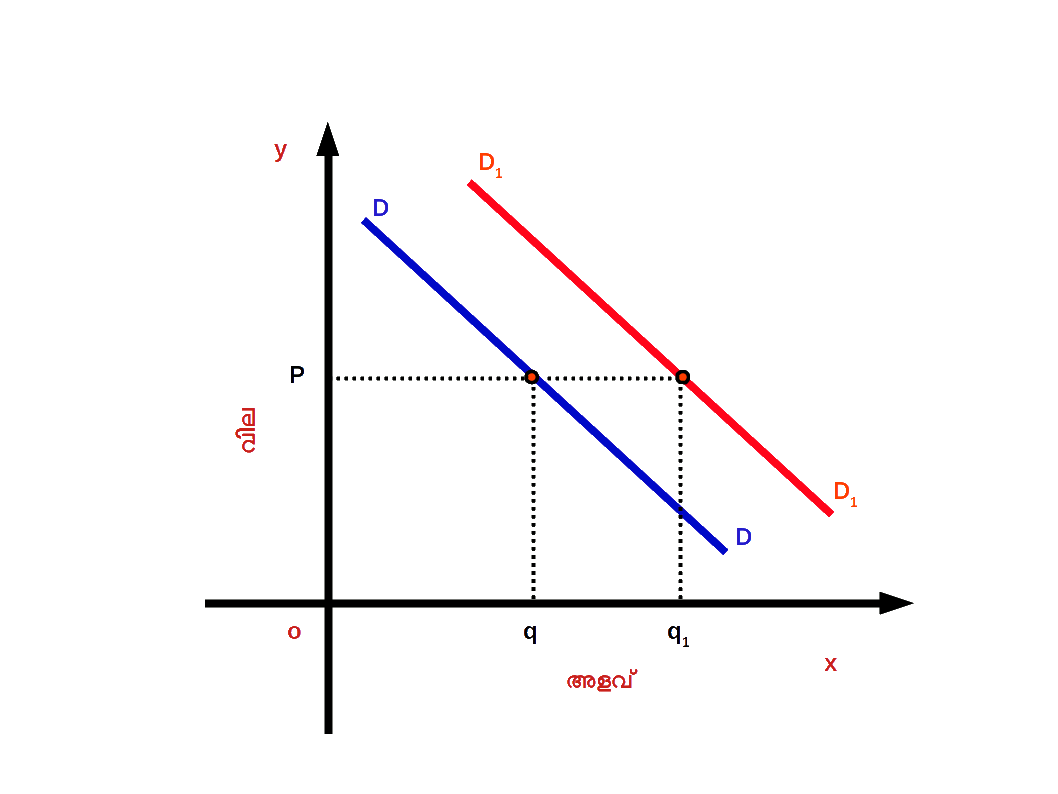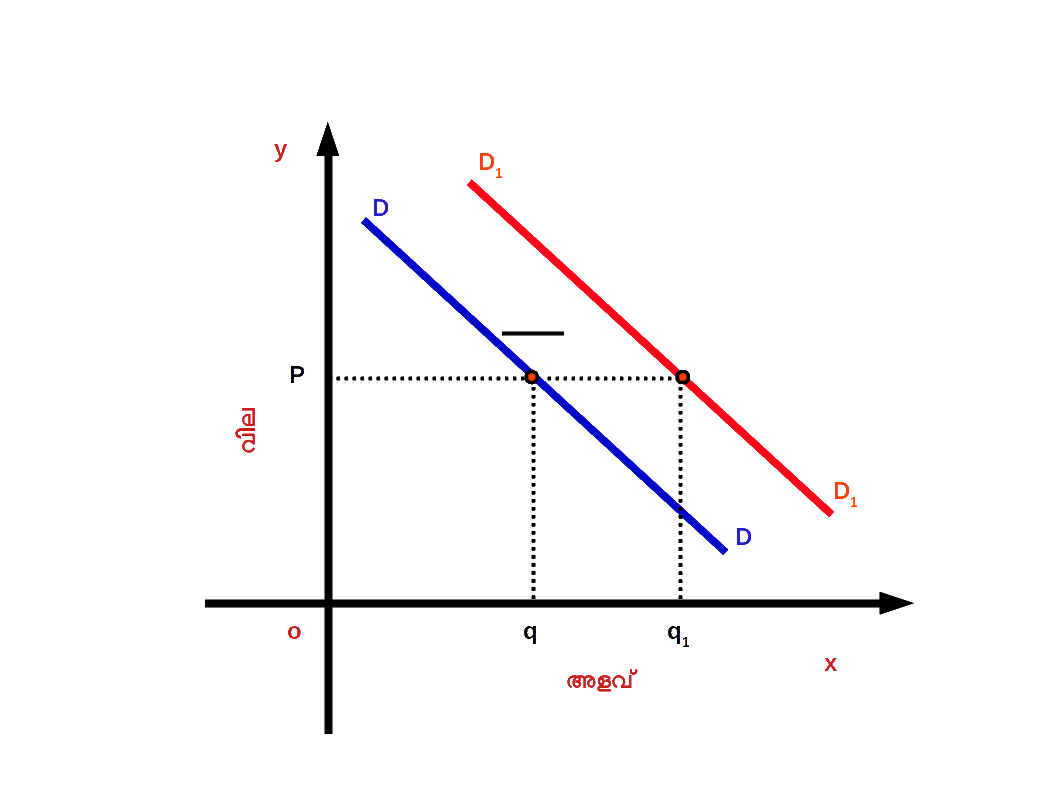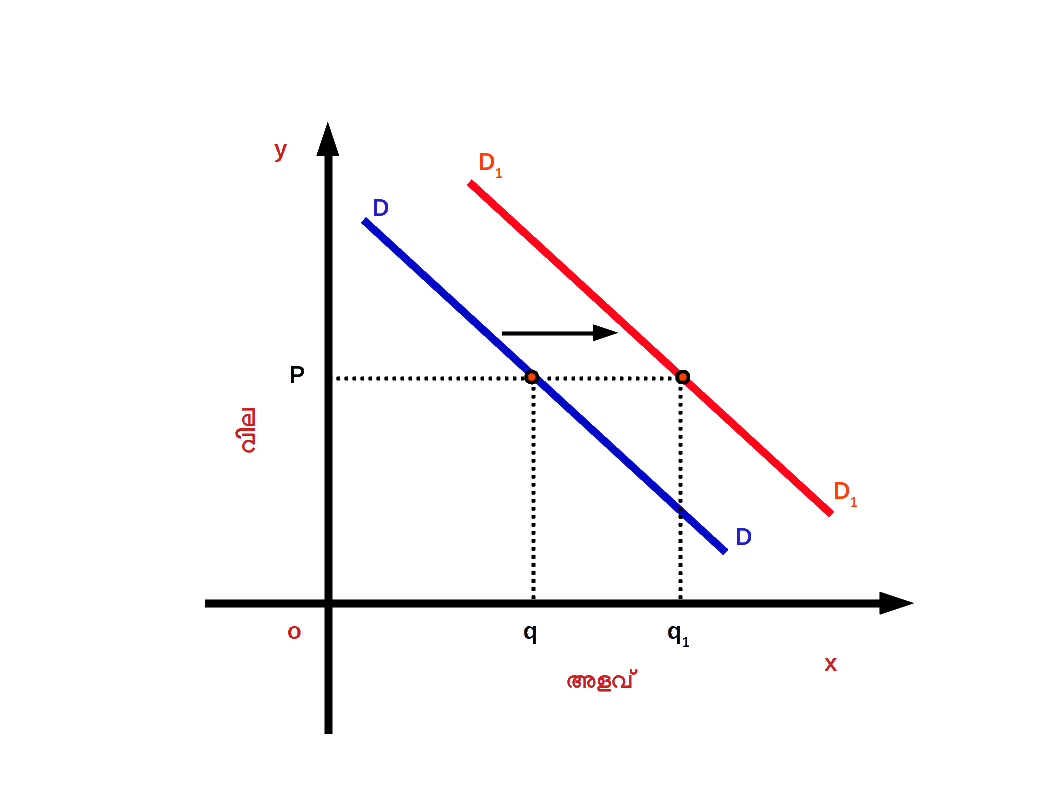Diagram 2.28

( b ) ചോദന കുറവ് ( Decrease in demand ) : വിലയിതര ഘടകങ്ങളിൽ പ്രതികൂലമായ മാറ്റത്തിന്റെ ഫലമായി ചോദന വക്രം ഇടതുഭാഗത്തേക്ക് മാറുന്നതിനെയാണ് ചോദന കുറവ് എന്നു പറയുന്നത്. ഡയഗ്രം 2.29 ൽ DD എന്നത് ആദ്യത്തെ ചോദന വക്രമാണ്. OP വിലയ്ക്ക് Oq സാധനം ചോദനം ചെയ്യുന്നു . വിലയിതര ഘടകങ്ങളിൽ പ്രതികൂലമായ മാറ്റമുണ്ടായതിന്റെ ഫലമായി DD എന്ന ചോദന വക്രം D₁D₁ എന്ന പുതിയ ചോദന വക്രമായി ഇടതുഭാഗത്തേക്ക് ചാടുന്നു അഥവാ മാറുന്നു. അപ്പോൾ ചോദനം Oq ൽ നിന്ന് Oq₁ ആയി കുറയുന്നു. വില OP യായി തുടരുന്നു ( മാറ്റമില്ല ). DD എന്ന ചോദന വക്രം D₁D₁ ആയി ഇടതു ഭാഗത്തേക്കുള്ള മാറ്റത്തെയാണ് ചോദന കുറവ് എന്നു പറയുന്നത്.

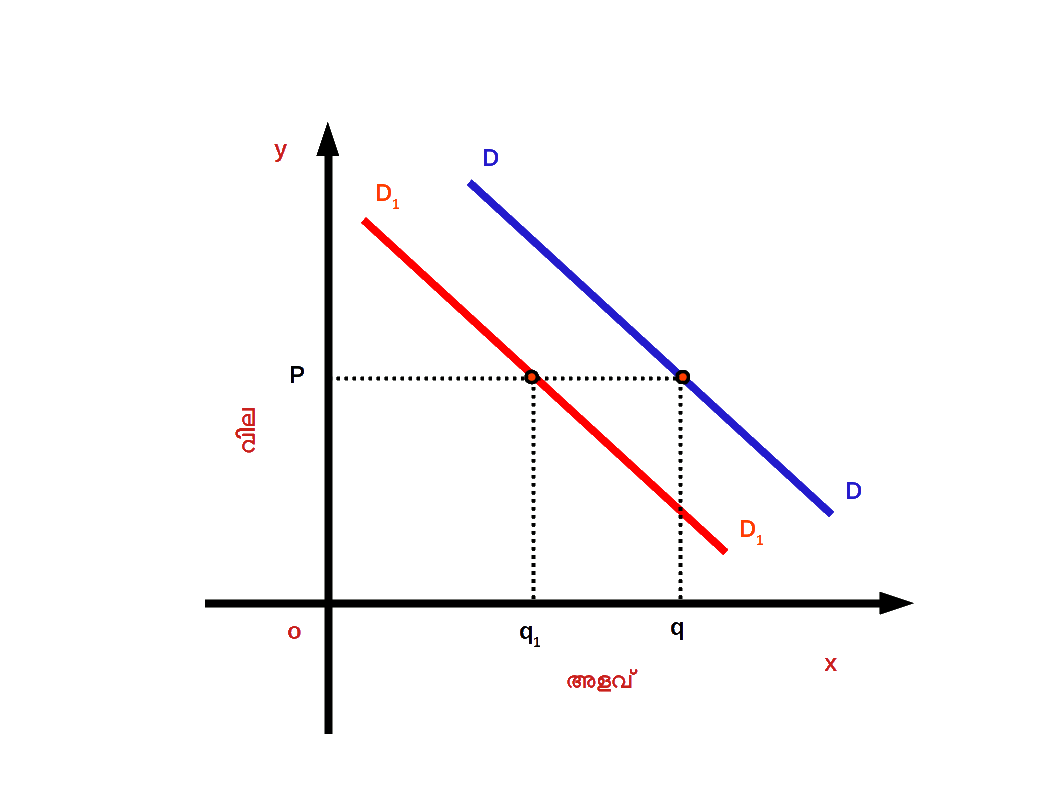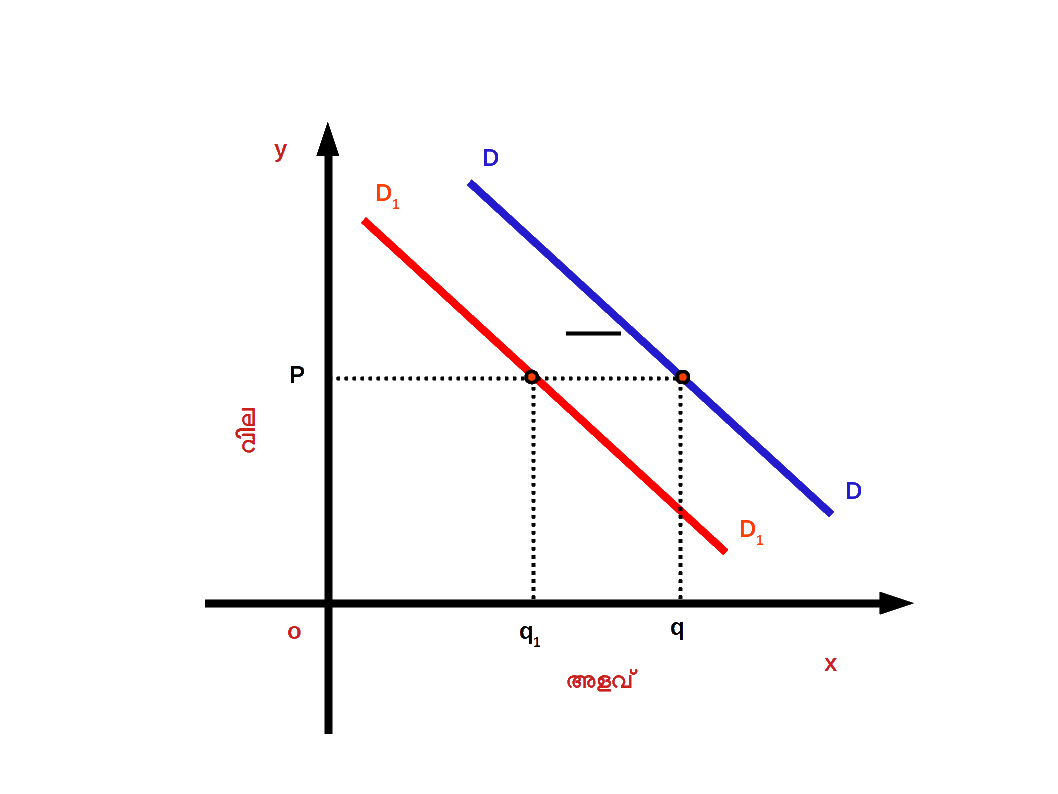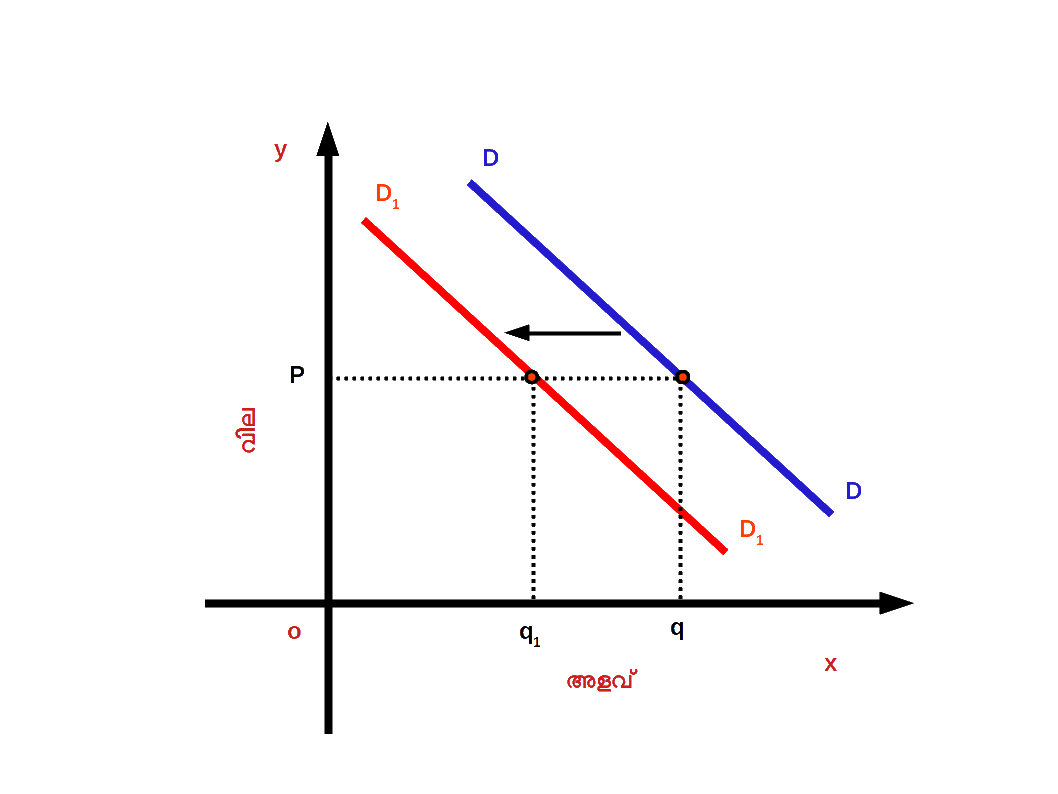Diagram 2.29

കമ്പോള ചോദനം ( Market Demand )
ഒരു നിശ്ചിത സമയത്ത് വിവിധ വിലയ്ക്ക് കമ്പോളത്തിലെ എല്ലാ ഉപഭോക്താക്കളും കൂടി വാങ്ങാൻ സന്നദ്ധമാകുന്ന ഒരു സാധനത്തിന്റെ അളവാണ് കമ്പോള ചോദനം. ഇത് വ്യക്തിഗത ചോദനത്തിന്റെ ആകെ തുകയാണ്. വ്യക്തിഗത ചോദന പട്ടികകളെ സമാന്തരമായി കുട്ടിയാണ് കമ്പോള ചോദന പട്ടിക ഉണ്ടാക്കുന്നത്. പട്ടിക 2.6 , 2.7 എന്നിവ രണ്ട് വ്യക്തിഗത ചോദന പട്ടികയാണ് . ഈ രണ്ട് വ്യക്തിഗത ചോദന പട്ടികയുടെ തുകയാണ് 2.8 എന്ന കമ്പോള പട്ടിക നിർമ്മിച്ചിരിക്കുന്നത് .

Table – Market Demand

ഉപഭോക്താവ് A (2.6) ഉപഭോക്താവ് B (2.7) കമ്പോള ചോദനം (2.8)
(ചോദനം A + ചോദനം B)

വില ചോദനം വില ചോദനം Price Demand

10 5 10 7 10 12

20 4 20 6 20 10

30 3 30 5 30 8

40 2 40 4 40 6

കമ്പോള ചോദന വക്രം ( Market Demand Curve )
ഒരു കമ്പോളത്തിലുള്ള എല്ലാ വ്യക്തികളുടെയും ചോദന വക്രങ്ങളെ സമാന്തരമായി കൂട്ടിയാൽ കമ്പോള ചോദന വക്രം ലഭിക്കും. കമ്പോളത്തിലുള്ള എല്ലാ വ്യക്തികളുടെയും ചോദനത്തിന്റെ ആകെ തുകയാണ് കമ്പോള ചോദന വക്രം. പട്ടിക 2.6 , 2.7 , 2.8 എന്നിവയുടെ അടിസ്ഥാനത്തിൽ കമ്പോള ചോദന വക്രം ഗ്രാഫ് 2.30 ൽ വരച്ചിരിക്കുന്നു. എന്നത് D_A , D_B എന്നീ ഉപഭോക്താക്കളുടെ വ്യക്തിഗത ചോദന വക്രമാണ്. MD എന്നത് കമ്പോള ചോദന വക്രവും.

Diagram 2.30

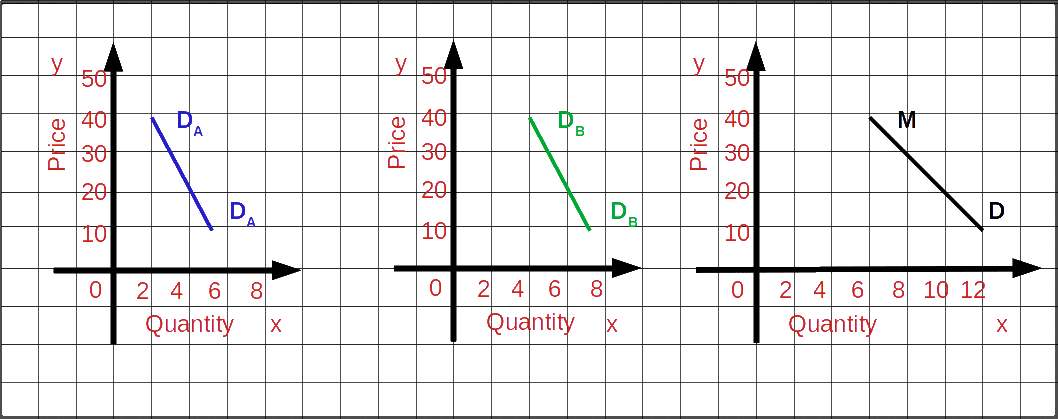
രണ്ട് രേഖീയ ചോദന വക്രങ്ങളുടെ കൂട്ടൽ ( Adding up of two Linear Demand Curves )
ഒരു കമ്പോളത്തിലെ രണ്ട് ഉപഭോക്താക്കളുടെ ചോദന സമവാക്യങ്ങൾ താഴെ കൊടുത്തിരിക്കുന്നു.
$$ {\,d_1(P) \,=\,10\,-\,P}\, ; \,{0\,≤\,P\,≤\,10}$$
$$ {\,= \,0\,;\,P\,>\,0} $$
$$ {\,d_2(P) \,=\,15\,-\,P}\, ; \,{0\,≤\,P\,≤\,15}$$
$$ {\,= \,0\,;\,P\,>\,0} $$
സാധനത്തിന്റെ വില 10 യോ അതിൽ കൂടുതലോ ആയാൽ ഒന്നാമത്തെ ഉപഭോക്താവിന്റെ ചോദനം 0 ആയിരിക്കും. അതുപോലെ , സാധന ത്തിന്റെ വില 15 യോ അതിൽ കൂടുതലോ ആയാൽ രണ്ടാമത്തെ ഉപഭോക്താവിന്റെ ചോദനം 0 ആയിരിക്കും.
കമ്പോള ചോദനം കണ്ടുപിടിക്കാൻ ഈ രണ്ട് വ്യക്തിഗത ചോദന സമവാക്യങ്ങൾ തമ്മിൽ കൂട്ടിയാൽ മതി. കമ്പോള ചോദന സമവാക്യം ( d_m ).
$$ {\,d_1(P) \,+\,d_2(P)} $$ $$ {\,=\,10\,-\,P\,+ \,15\,-\,P}$$
$$ {d_(m)\, = 25 \,-\,2P\,;} $$ $$ {\,0\,≤\,P\,≤\,\frac{25}{2}} $$
$$ {0\, = 25 \,;\,P\,>\,\frac{25}{2}} $$

ചോദനത്തിന്റെ വില ഇലാസ്തികത ( Price Elasticity of Demand )
ആൽഫ്രഡ് മാർഷലാണ് ഇലാസ്തികത എന്ന ആശയം സാമ്പത്തിക ശാസ്ത്രത്തിൽ ആദ്യമായി ഉപയോഗിച്ചത്. വിലയിലുള്ള മാറ്റം മൂലം ചോദനത്തിന്റെ അളവിൽ എത്രമാത്രം മാറ്റം ഉണ്ടാകുന്നുവെന്ന് നിർണ്ണയിക്കാൻ വില ഇലാസ്തികതയ്ക്ക് കഴിയുന്നു. ഇലാസ്തികത എന്ന പദത്തിന്റെ അർത്ഥം പ്രതിസ്പന്ദനാത്മകത എന്നാണ്. “ ഒരു സാധനത്തിന്റെ വിലയിലെ മാറ്റം മൂലം ആ സാധനത്തിന്റെ ചോദനത്തിന്റെ അളവിലുണ്ടാകുന്ന പ്രതിസ്പന്ദനാത്മകതയെ ചോദനത്തിന്റെ വില ഇലാസ്തികത എന്നു പറയുന്നു.”
ചോദനത്തിന്റെ അളവിലുള്ള മാറ്റത്തിന്റെ ശതമാനത്തെ വിലയിലുള്ള മാറ്റത്തിന്റെ ശതമാനം കൊണ്ട് ഹരിച്ച് വില ഇലാസ്തികത കണക്കാക്കാം.

വില ഇലാസ്തികതയുടെ തോതുകൾ അഥവാ തീവ്രതകൾ ( Degree of Price Elasticity )
ഓരോ സാധനത്തിന്റെയും ഇലാസ്തികത വ്യത്യസ്തമായിരിക്കും. ചോദനത്തിന്റെ അളവിലുള്ള മാറ്റത്തിന്റെ തോത് അഥവാ തീവ്രതയനുസരിച്ച് ഇലാസ്തികതയെ അഞ്ചായി തിരിച്ചിരിക്കുന്നു. അവ:

( 1 ) ഇലാസ്തിക ചോദനം ( Elastic demand )
ഇലാസ്തിക ചോദനത്തെ ഉയർന്ന ഇലാസ്തിക ചോദനം എന്നു പറയാറുണ്ട്. ചോദനത്തിലുള്ള ശതമാനമാറ്റം വിലയിലുള്ള ശതമാനമാറ്റത്തെക്കാൾ കൂടുതലാണെങ്കിൽ ഇലാസ്തിക ചോദനം എന്നു പറയുന്നു. ഉദാഹരണമായി വിലയിൽ 10 % മാറ്റമുണ്ടാകുമ്പോൾ ചോദനത്തിൽ 30 % മാറ്റമുണ്ടാകുന്നു. ഉയർന്ന ഇലാസ്തിക ചോദനമായിരിക്കുമ്പോൾ ഇലാസ്തികതയുടെ കേവല മൂല്യം ഒന്നിനെക്കാൾ ഉയർന്നിരിക്കും. നമ്മുടെ ഉദാഹരണത്തിൽ e = 30 % ÷ 10 % = 3 അപ്പോൾ ചോദന വക്രം ഡയഗ്രം 2.31 ൽ കാണുന്നതു പോലെ കൂടുതൽ പരന്നതായിരിക്കും.

Diagram 2.31

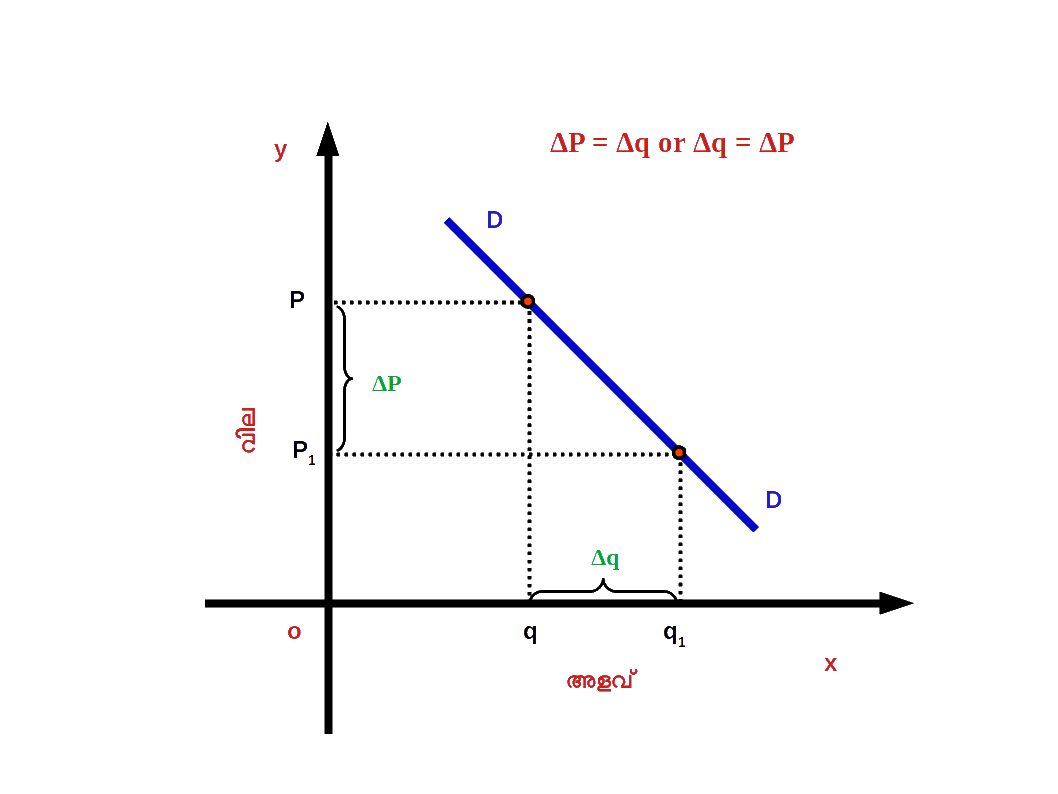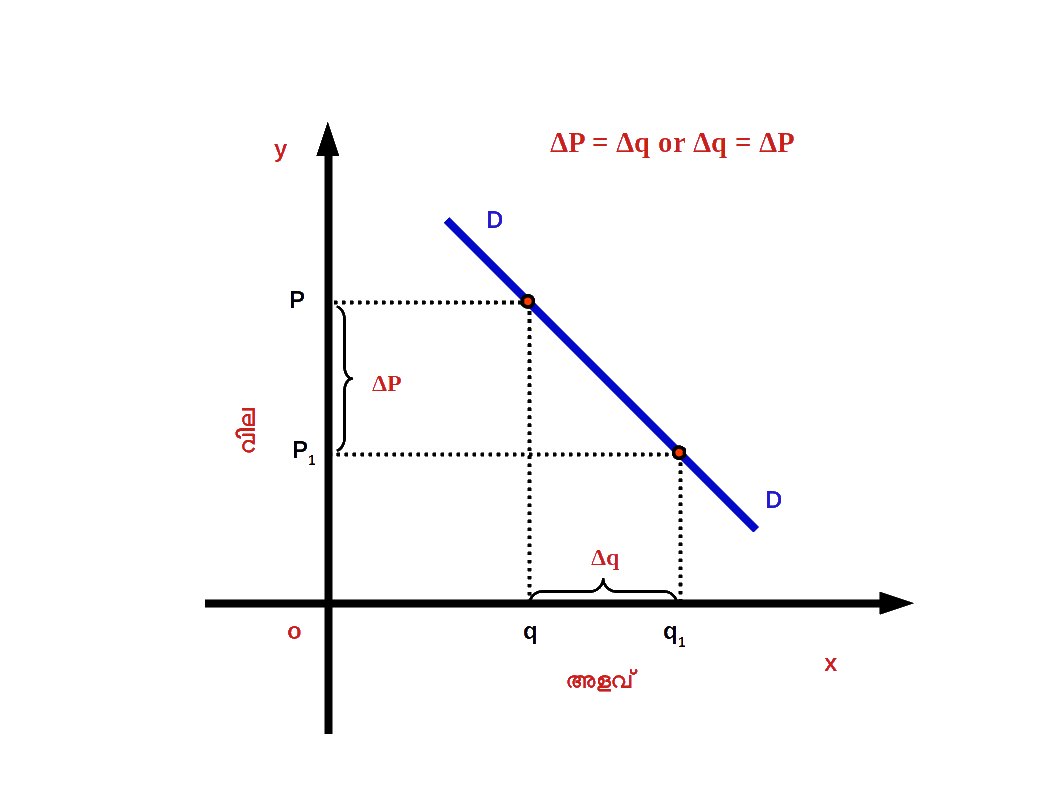
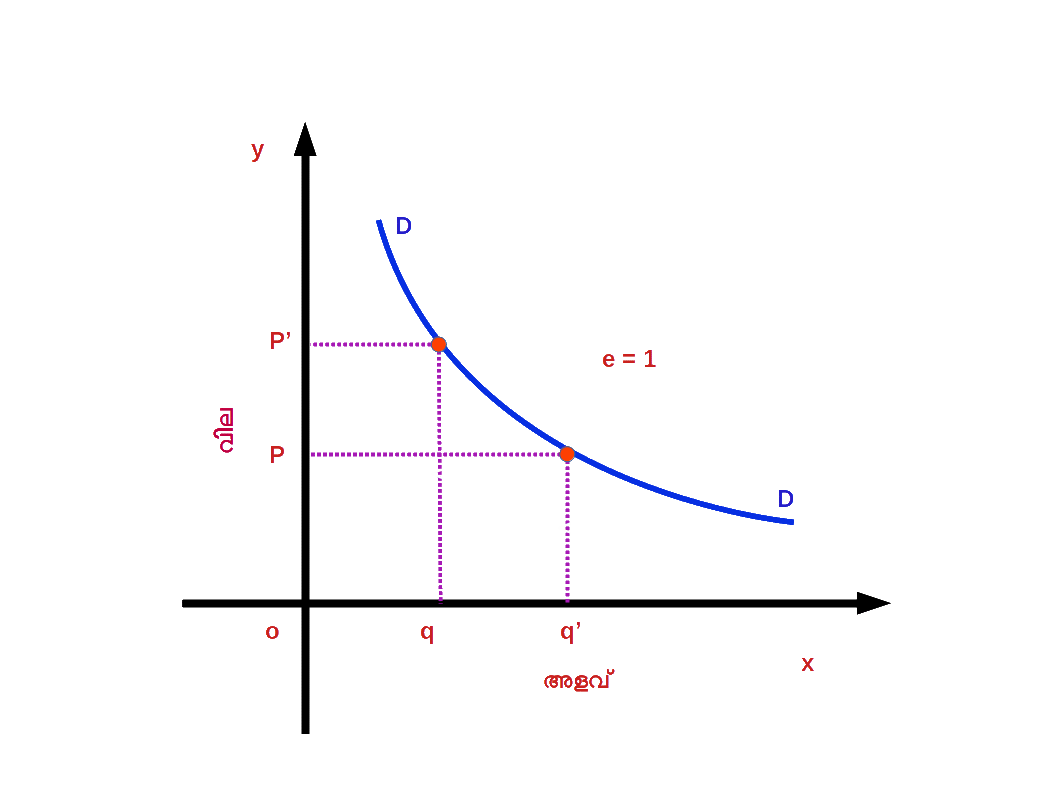
( 2 ) ഏകാത്മക ഇലാസ്തിക ചോദനം ( Unitary elastic demand )
ചോദനത്തിലുള്ള ശതമാന മാറ്റവും വിലയിലുള്ള ശക്തമായ മാറ്റവും തുല്യമാണെങ്കിൽ ഏകാത്മക ഇലാസ്തിക ചോദനം എന്നു പറയുന്നു. ഉദാഹരണമായി വിലയിൽ 10 ശതമാനം മാറ്റമുണ്ടാ കുമ്പോൾ ചോദനത്തിലും 10 ശതമാനം മാറ്റമുണ്ടാകുന്നു. ഏകാത്മക ഇലാസ്തിക ചോദനമായിരിക്കുമ്പോൾ ഇലാസ്തികതയുടെ കേവല മൂല്യം ഒന്നായിരിക്കും. നമ്മുടെ ഉദാഹരണത്തിൽ e = 10 % ÷ 10 % = 1 അപ്പോൾ ചോദന വക്രം 2.32 ൽ കാണുന്നതുപോലെ moderate slope ആയിരിക്കും.

Diagram 2.32

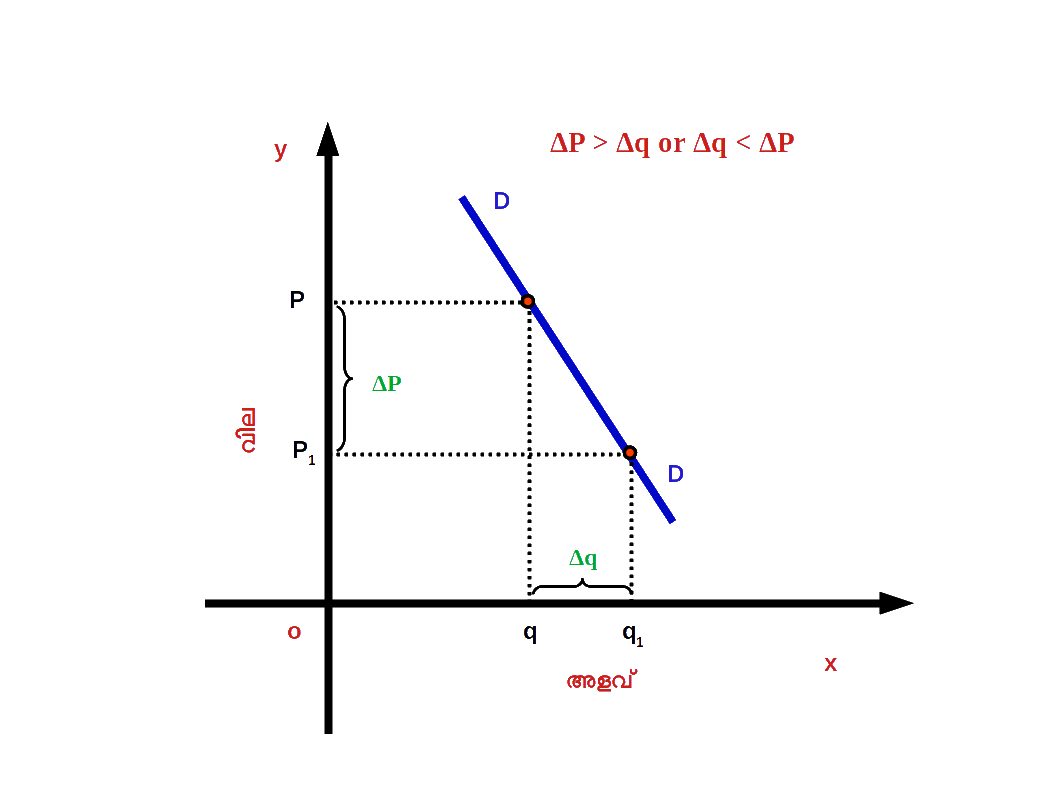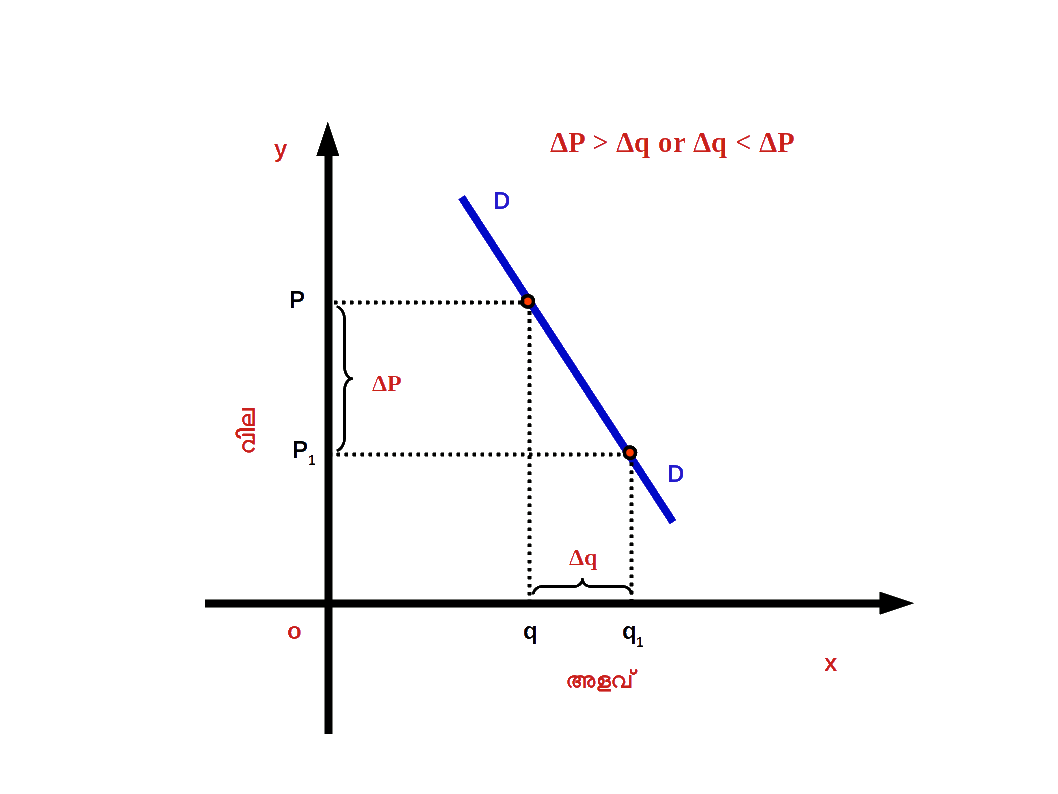
( 3 ) ഇലാസ്തികമല്ലാത്ത ചോദനം ( Inelastic demand )
ചോദനത്തിലുള്ള ശതമാനമാറ്റം വിലയിലുള്ള ശതമാനമാറ്റത്തെക്കാൾ കുറവാണെങ്കിൽ ഇലാസ്തികമല്ലാത്ത ചോദനം എന്നു പറയുന്നു. ഉദാഹരണമായി വിലയിൽ 20 ശതമാനം മാറ്റമുണ്ടായപ്പോൾ ചോദനത്തിൽ 10 ശതമാനം മാറ്റമുണ്ടാകുന്നു. ഇലാസ്തികമല്ലാത്ത ചോദനമായിരിക്കുമ്പോൾ ഇലാസ്തികതയുടെ കേവലമൂല്യം ഒന്നിനെക്കാൾ കുറവായിരിക്കും . നമ്മുടെ ഉദാഹരണത്തിൽ 10 % ÷ 20 % = = 0.5. ഇത്തരം സാഹചര്യത്തിൽ ചോദന വക്രം ഡയഗ്രം 2.33 ൽ കാണുന്നതു പോലെ കുറഞ്ഞ പരപ്പായിരിക്കും.

Diagram 2.33

( 4 ) പൂർണ്ണ ഇലാസ്തിക ചോദനം ( Perfectly elastic demand )
വിലയിലുണ്ടാകുന്ന ഒരു ചെറിയ മാറ്റം ചോദനത്തിൽ അനന്തമായ മാറ്റം ഉണ്ടാക്കുന്ന അവസ്ഥയാണ് പൂർണ്ണ ഇലാസ്തിക ചോദനം. ഇത്തരം സാഹചര്യത്തിൽ ഇലാസ്തികതയുടെ കേവലമൂല്യം അനന്തമായിരിക്കും. ചോദന വക്രം ഡയഗ്രം 2.34 ൽ കാണുന്ന പോലെ x അക്ഷത്തിന് സമാന്തരമായിരിക്കും.

Diagram 2.34

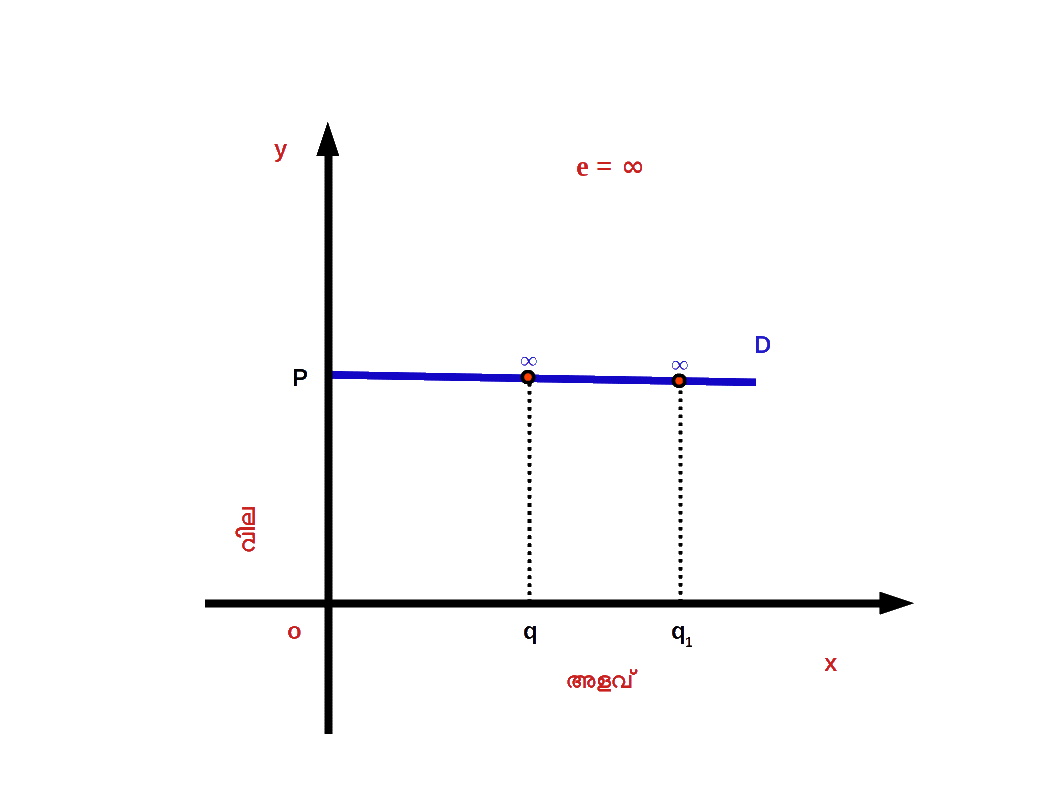
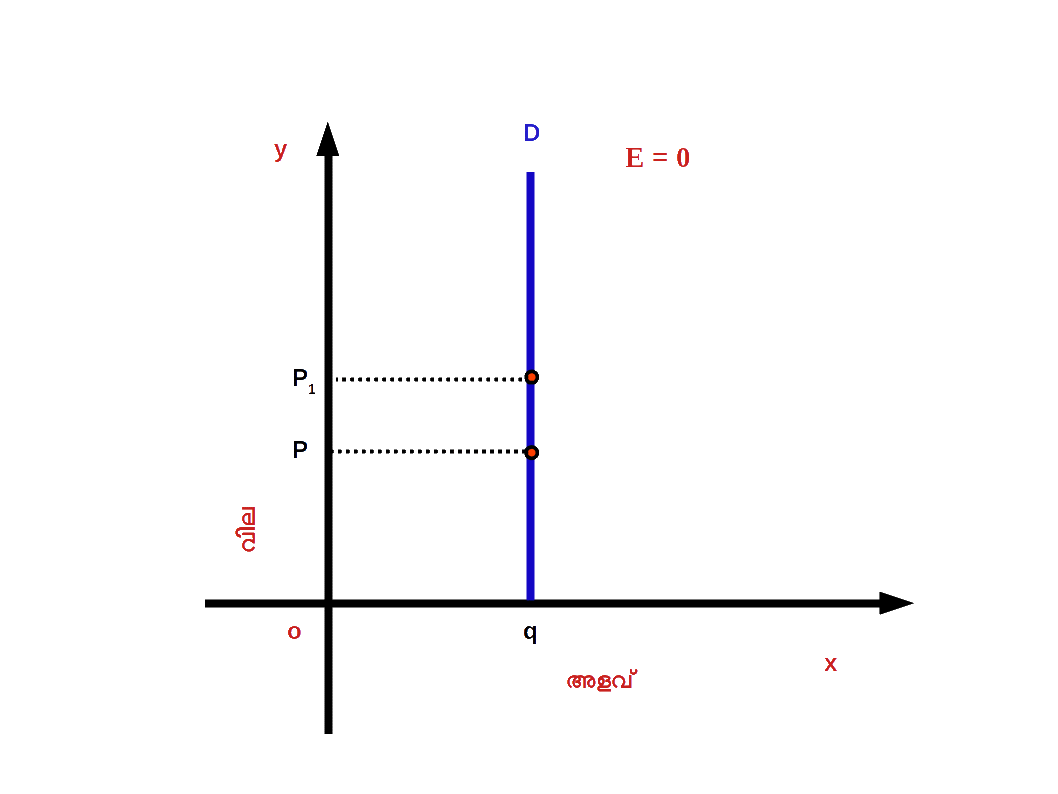
( 5 ) പൂർണ്ണ ഇലാസ്തികമല്ലാത്ത ചോദനം ( Perfectly inelastic demand )
വിലയിൽ എത്ര മാറ്റമുണ്ടായാലും ചോദനത്തിൽ യാതൊരുവിധ മാറ്റവും ഉണ്ടാകാത്ത അവസ്ഥയാണ് പൂർണ്ണ ഇലാസ്തികമല്ലാത്ത ചോദനം. ഇത്തരം സാഹചര്യങ്ങളിൽ ഇലാസ്തികതയുടെ മൂല്യം പൂജ്യമായിരിക്കും. അപ്പോൾ ചോദന വക്രം ഡയഗ്രം 2.35 ൽ കാണുന്നതുപോലെ y അക്ഷത്തിന് ലംബമായിരിക്കും.

Diagram 2.35

വില ഇലാസ്തികത അളക്കുന്ന രീതികൾ ( Methods of measuring price elasticity of demand )
വില ഇലാസ്തികത അളക്കുന്നത് പ്രധാനമായും മൂന്നു വിധത്തിലാണ്. അവ:

( 1 ) ശതമാന രീതി

( 2 ) രേഖീയ ചോദന വക്രത്തിലെ വിവിധ ബിന്ദുക്കളിലെ ഇലാസ്തികത നിർണ്ണയിക്കുന്ന രീതി

( 3 ) ചെലവ് രീതി

( 1 ) ശതമാന രീതി ( Percentage method )
ശതമാന രീതി അനുസരിച്ച് , ചോദനത്തിന്റെ അളവിലുള്ള മാറ്റത്തിന്റെ ശതമാനത്തെ വിലയിലുള്ള മാറ്റത്തിന്റെ ശതമാനം കൊണ്ട് ഹരിച്ചാണ് ചോദനത്തിന്റെ വില ഇലാസ്തികത നിർണ്ണയിക്കുന്നത്. അതായത് , ചോദനത്തിന്റെ വില ഇലാസ്തികത ( e ) :
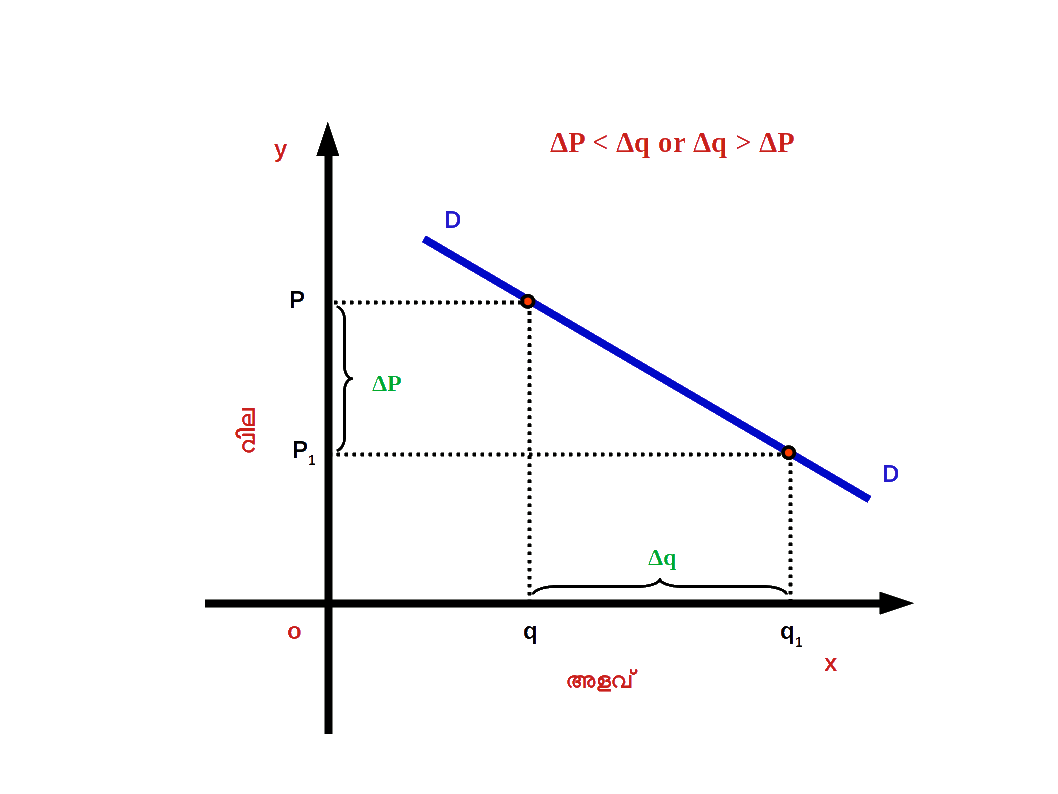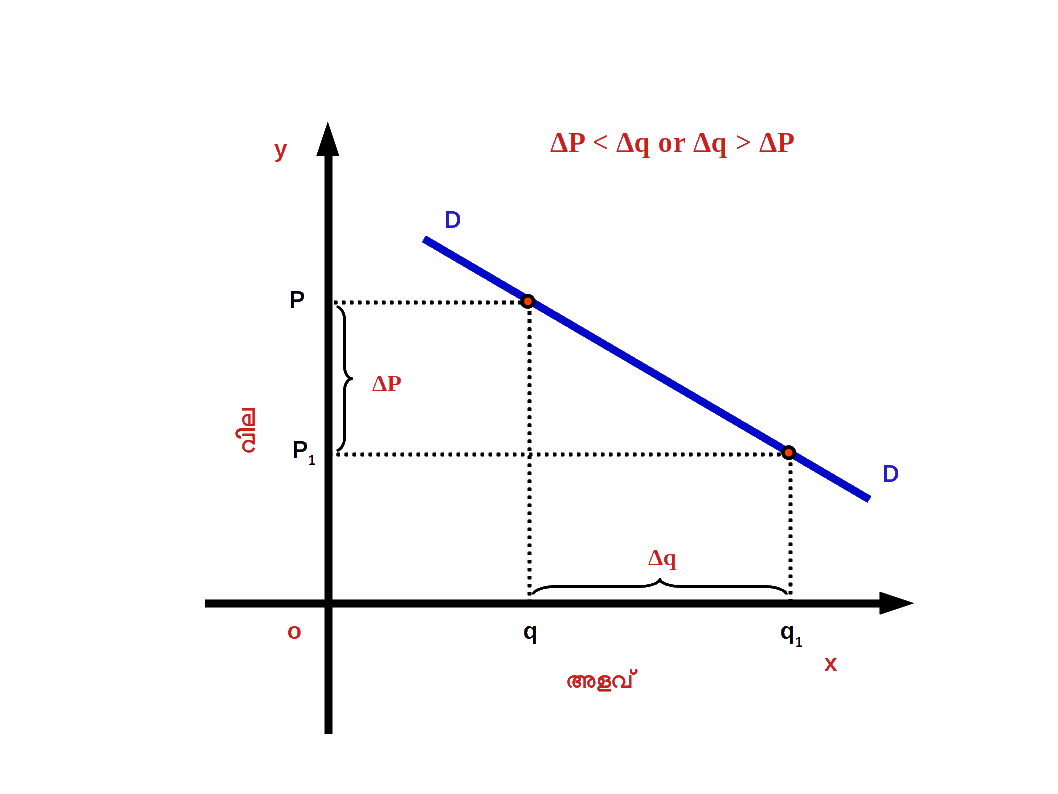
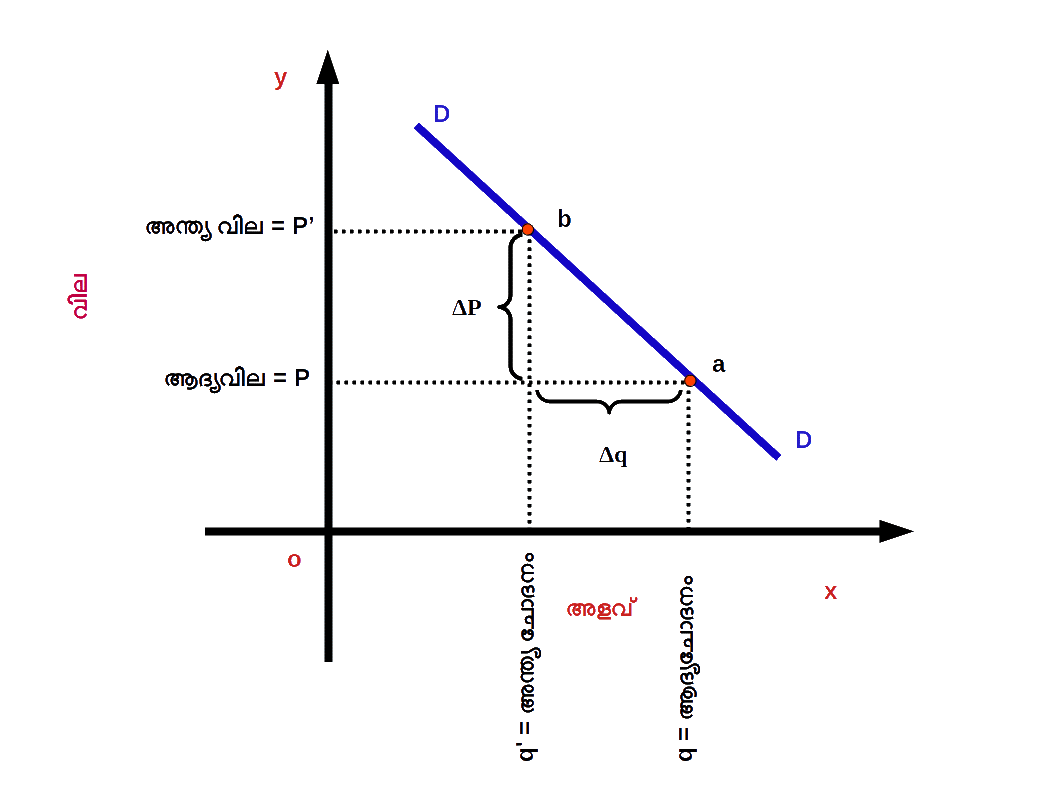
ഡയഗ്രം 2.36 ൽ കൊടുത്തിരിക്കുന്ന DD എന്ന ചോദന വക്രം പരിഗണിക്കുക. സാധനത്തിന്റെ വില P ൽ നിന്ന് P’ ആയി വർധിച്ചപ്പോൾ ചോദനത്തിന്റെ അളവ് q ൽ നിന്ന് q’ ആയി കുറയുന്നുവെന്ന് കരുതുക. അപ്പോൾ വിലയിലെ മാറ്റം ΔP (= P’ – P) യും ചോദനത്തിന്റെ അളവിലെ മാറ്റം Δq (=q’ – q) യും മാണ്. ഇവിടെ P ആദ്യവിലയും q ആദ്യചോദനവുമാണ്.

Diagram 2.36

അപ്പോൾ ,
$$ \mathbf {e \,=\,{\frac{{\frac{Δq}{q}}× 100}{{\frac{ΔP}{P}}× 100}}} $$
$$ \mathbf {e \,=\,{{{{\frac{Δq}{q}}}}÷{{{\frac{ΔP}{P}}}}}} $$
$$ \mathbf {=\,{{{{\frac{Δq}{q}}}}×{{{\frac{P}{ΔP}}}}}} $$
സാധനത്തിന്റെ വില രൂപയിലും ( ഡോളർ ) ചോദനത്തിന്റെ അളവ് കിലോഗ്രാമിലും ( ലിറ്റർ അല്ലെങ്കിൽ പൗണ്ട് ) അളക്കുന്നതുകൊണ്ട് ഇലാസ്തികതയുടെ മൂല്യം യൂണിറ്റില്ലാത്ത ഒരു നമ്പർ ആയിരിക്കും. അതുപോലെ വിലയും ചോദനത്തിന്റെ അളവും എതിർദിശയിൽ മാറുന്നതുകൊണ്ട് ഇലാസ്തികതയുടെ മൂല്യം ഒരു നെഗറ്റീവ് സംഖ്യ ആയിരിക്കും. എന്നാൽ വില ഇലാസ്തികതയുടെ കേവലമൂല്യമാണ് എപ്പോഴും ഉപയോഗിക്കാറ്.
EXAMPLE 2.19 പെട്രോളിന്റെ വില ലിറ്ററിന് 60 ൽ നിന്ന് 70 യായി വർധിച്ചപ്പോൾ അതിന്റെ ചോദനം 100 ലിറ്ററിൽനിന്ന് 80 ലിറ്ററായി കുറഞ്ഞു. അപ്പോൾ പെട്രോളിന്റെ വില ഇലാസ്തികത കാണുന്നത് എങ്ങനെയെന്ന് നോക്കാം.
പെട്രോളിന്റെ ആദ്യവില = P = 60
പെട്രോളിന്റെ അന്ത്യവില = P’ = 70
വിലയിലെ മാറ്റം P’ – P = ΔP = 10
പെട്രോളിന്റെ ആദ്യ ചോദനം q = 100 ലിറ്റർ
പെട്രോളിന്റെ അന്ത്യ ചോദനം q’ = 80 ലിറ്റർ
ചോദനത്തിലെ മാറ്റം q’ – q = Δq = -20 ലിറ്റർ
പെട്രോളിന്റെ വില ഇലാസ്തികത = e = $ {\frac{Δq}{ΔP}}×{\frac{P}{q}} $

= $ {\frac{Δq}{ΔP}}×{\frac{P}{q}} $
= $ {\frac{-\,20}{10}}×{\frac{60}{100}} $
= $ {\frac{-\,1200}{1000}} $
=-1.2

e = -1.2 എന്നത് യൂണിറ്റില്ലാത്ത ഒരു നെഗറ്റീവ് സംഖ്യയാണ്. -1.2 ന്റെ കേവലവില 1.2 ആണ്. അതുകൊണ്ട് |e| = 1.2 എന്ന് നാം പരിഗണിക്കുന്നു.|e| > 1 or e < -1.2 ആയതുകൊണ്ട് ഇത് ഉയർന്ന ഇലാസ്തിക ചോദനമാണ്.
ചിലപ്പോൾ വിലയിലെയും ചോദനത്തിലെയും മാറ്റം ശതമാന രൂപത്തിൽ തന്നിരിക്കാം. അത്തരം സാഹചര്യങ്ങളിൽ വില ഇലാസ്തികത കാണുന്ന തെങ്ങനെയെന്ന് example 2.20 കാണുക.
EXAMPLE 2.20 ഒരു സാധനത്തിന്റെ വിലയിൽ 10 ശതമാനം വർധനവുണ്ടായപ്പോൾ ചോദനത്തിൽ 8 ശതമാനം കുറവുവന്നുവെങ്കിൽ വില ഇലാസ്തികത എന്തായിരിക്കും ?

e = $ {\frac{8%}{10%}} $
= $ {\frac{8}{10}} $
= 0.8

( 2 ) ഒരു രേഖീയ ചോദന വക്രത്തിലെ വിവിധ ബിന്ദുക്കളിലെ ഇലാസ്തികത നിർണ്ണയിക്കുന്ന വിധം ( Measurement of elasticity along a linear demand curve )
ബിന്ദുരീതി എന്നും ഇത് അറിയപ്പെടുന്നു. ഒരു രേഖീയ ചോദനത്തിലെ ഓരോ ബിന്ദുവിലെയും ഇലാസ്തികത വ്യത്യസ്തമായിരിക്കും. q = a – bp എന്ന രേഖീയ ചോദന വക്രം പരിഗണിക്കുക. വിലയിലുള്ള ഒരു യൂണിറ്റ് മാറ്റം ചോദനത്തിലുള്ള മാറ്റം $ {\frac{Δq}{ΔP}} $ = -b ആണ്.
e = $ {\frac{Δq}{ΔP}} $ $ {\frac{P}{q}} $ ആയതുകൊണ്ട്
e = $ {\frac{-bP}{q}} $ ($ {\frac{Δq}{ΔP}} $ -b ആയതുകൊണ്ട് )
e = $ {\frac{-bP}{a\,-\,bP}} $ (q = a – bP ആയതുകൊണ്ട് )
P യിലും q യിലും മാറ്റമുണ്ടാകുന്നതിനനുസരിച്ച് ഇലാസ്തികതയുടെ മൂല്യത്തിലും മാറ്റം വരുന്നു.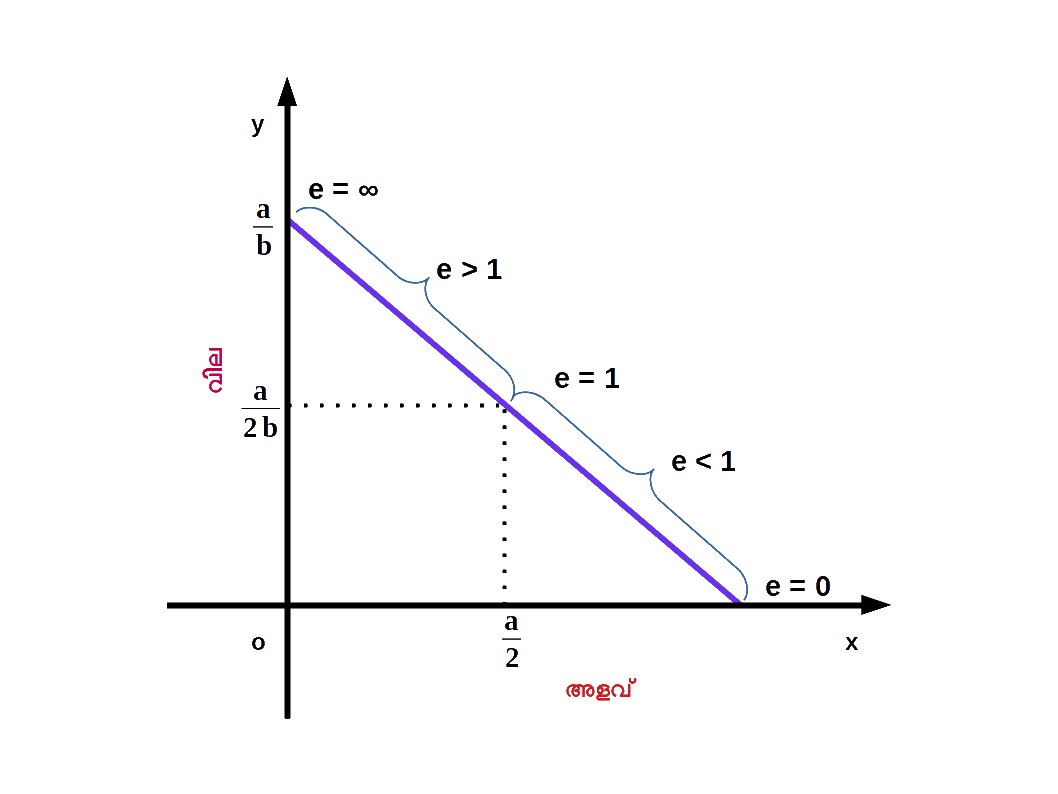

Diagram 2.37

ഡയഗ്രം 2.37 ൽ ഒരു രേഖീയ ചോദന വക്രത്തിലെ വിവിധ ബിന്ദുക്കളിലെ ഇലാസ്തികത കാണിക്കുന്നു.

( 1 ) രേഖീയ ചോദന വക്രം x – അക്ഷത്തിൽ ഖണ്ഡിക്കുന്ന ബിന്ദുവിൽ ഇലാസ്തികത പൂജ്യമായിരിക്കും. ഡയഗ്രം 2.37 ൽ കാണുക.

( 2 ) രേഖീയ ചോദന വക്രം y – അക്ഷത്തിൽ ഖണ്ഡിക്കുന്ന ബിന്ദുവിലെ ഇലാസ്തികത അനന്തമായിരിക്കും.

( 3 ) ചോദന വക്രത്തിലെ മധ്യ ബിന്ദുവിലെ ഇലാസ്തികത ഒന്ന് ആയിരിക്കും.

( 4 ) മധ്യബിന്ദുവിനും X – അക്ഷത്തെ ഖണ്ഡിക്കുന്ന ബിന്ദുവിനുമിടയിൽ ഇലാസ്തികത ഒന്നിനേക്കാൾ കുറവായിരിക്കും.

( 5 ) മധ്യബിന്ദുവിനും y – അക്ഷത്തെ ഖണ്ഡിക്കുന്ന ബിന്ദുവിനുമിടയിൽ ഇലാസ്തികത ഒന്നിനേക്കാൾ കൂടുതലായിരിക്കും.

EXAMPLE 2.21 : q = 20 -2P എന്ന രേഖീയ ചോദന വക്രത്തിൽ വില 5 യാണെങ്കിൽ വില ഇലാസ്തികത എത്രയാണെന്ന് നോക്കാം. ഇലാസ്തികത കാണാനുള്ള സൂത്രവാക്യം :

e = $ {\frac{-bP}{a\,-\,bP}} $ ആയതിനാൽ,
-b = 2 , a = 20 , P = 5.
അപ്പോൾ ,
e = $ {\frac{-2 × 5}{20\,-\,2 × 5}} $
= $ {\frac{-10}{20\,-\,10}} $
= $ {\frac{-10}{10}} $
= – 1
|e| = 1

ജ്യാമിതീയ രീതിയനുസരിച്ച് ഇലാസ്തികത കാണുന്ന വിധം ( Geometric measure of elasticity )
x – അക്ഷത്തിലും y – അക്ഷത്തിലും ഖണ്ഡിച്ചിരിക്കുന്ന ഒരു രേഖീയ ചോദന വക്രത്തിലെ വിവിധ ബിന്ദുക്കളിലെ ഇലാസ്തികത ജ്യാമിതീയ രീതി ഉപയോഗിച്ച് നമുക്ക് വളരെ എളുപ്പത്തിൽ കാണാവുന്നതാണ്. ഈ രീതിയനുസരിച്ച് രേഖീയ ചോദന വക്രത്തിലെ ഇലാസ്തികത കാണേണ്ട ബിന്ദുവിന് താഴെയുള്ള ഖണ്ഡത്തെ ബിന്ദുവിന് മുകളിലുള്ള ഖണ്ഡം കൊണ്ട് ഹരിച്ചാൽ മതി.
അതായത്,
ഡയഗ്രം 2.38 ൽ കൊടുത്തിരിക്കുന്ന AB ചോദന വക്രത്തിലെ ഒരു ബിന്ദുവാണ് C. BC എന്ന കീഴണ്ഡത്തിന്റെ നീളം 15 cm ഉം AC എന്ന മേൽഖണ്ഡത്തിന്റെ നീളം 10 cm ഉം ആണെന്ന് കരുതുക . അപ്പോൾ ,

e = $ {\frac{15\,CM}{10\,CM}} $
= 1.5.

( 3 ) ചെലവു രീതി ( Expenditure method )
ചെലവ് രീതിയെ Outlay method എന്നു പറയാറുണ്ട്. ഒരു സാധനത്തിന്റെ വിലയെ അതിന്റെ ചോദനത്തിന്റെ അളവുകൊണ്ട് ഗുണിച്ചാണ് ചെലവു കാണുന്നത്. അതായത് , E = pq. ചെലവ് രീതി അനുസരിച്ച് വിലയിലുള്ള മാറ്റവും ചെലവിലുള്ള മാറ്റവും തമ്മിൽ താരതമ്യം ചെയ്താണ് ഇലാസ്തികത നിർണ്ണയിക്കുന്നത്. ഈ രീതി പ്രകാരം ഇലാസ്തികത ഒന്നിൽ കൂടുതലാണോ , ഒന്നാണോ , ഒന്നിൽ കുറവാണോ എന്ന് കണ്ടെത്താൻ കഴിയും.

( 1 ) വിലയിലുണ്ടാകുന്ന മാറ്റത്തിന്റെ വിപരീത ദിശയിലാണ് ചെലവ് മാറുന്നതെങ്കിൽ ഇലാസ്തികത ഒന്നിൽ കൂടുതലായിരിക്കും. അതായത് , വില വർധിക്കുമ്പോൾ ചെലവു കുറയുകയും വില കുറയുമ്പോൾ ചെലവ് വർധിക്കുകയും ചെയ്യുകയാണെങ്കിൽ ഉയർന്ന ഇലാസ്തിക ചോദനം ആയിരിക്കും.

( 2 ) വിലയിൽ മാറ്റമുണ്ടാകുമ്പോൾ ചെലവിൽ യാതൊരു വിധ മാറ്റവും ഉണ്ടാകുന്നില്ലെങ്കിൽ ഇലാസ്തികത ഒന്നായിരിക്കും. അതായത് , വില മാറുന്നതിനനുസരിച്ച് ചെലവിൽ മാറ്റം ഇല്ലാത്ത അവസ്ഥയിൽ ഏകാത്മക ഇലാസ്തിക ചോദനമായിരിക്കും.

( 3 ) വിലയിലുണ്ടാകുന്ന മാറ്റത്തിന്റെ അതേ ദിശയിൽ തന്നെയാണ് ചെലവും മാറുന്നതെങ്കിൽ ഇലാസ്തികത ഒന്നിനേക്കാൾ കുറവായിരിക്കും. അതായത് , വില വർധിക്കുമ്പോൾ ചെലവ് വർധിക്കുകയും വില കുറയുമ്പോൾ ചെലവ് കുറയുകയും ചെയ്യുകയാണങ്കിൽ കുറഞ്ഞ ഇലാസ്തിക ചോദനമായിരിക്കും.

വിലയും ചെലവും ഇലാസ്തികതയും തമ്മിലുള്ള ബന്ധം പട്ടിക 2.9 ൽ കൊടുത്തിരിക്കുന്നു.

Table 2.9 ചെലവു രീതി

വില (P) ചോദനത്തിന്റെ അളവ് (q) ചെലവ് ഇലാസ്തികത

10 5 50 e > 1

15 3 45

10 6 60 e = 1

15 4 60

10 7 70 e < 1

15 6 90

സ്ഥിര ഇലാസ്തിക ചോദന വക്രങ്ങൾ ( Constant elasticity demand curves )
ഒരു രേഖീയ ചോദന വക്രത്തിലെ വിവിധ ബിന്ദുക്കളിലെ ഇലാസ്തികത 0 മുതൽ ∞ വരെയുള്ള ഏതു മൂല്യവുമാകാം. എന്നാൽ ഏതാനും ചില ചോദന വക്രങ്ങളിലെ ഇലാസ്തികത എല്ലാ ബിന്ദുക്കളിലും സ്ഥിരമായിരിക്കും. ഉദാഹരണമായി ഡയഗ്രം 2.38 ൽ കൊടുത്ത അപൂർണ്ണ ഇലാസ്തിക ചോദനത്തെ സൂചിപ്പിക്കുന്ന ലംബ ചോദനത്തിലെ ഏതൊരു ബിന്ദുവിലെയും ഇലാസ്തികത എപ്പോഴും പൂജ്യമായിരിക്കും.

Diagram 2.38

ഈ ചോദന വക്രത്തിൽ വിലയിൽ എത്ര മാറ്റമുണ്ടായാലും ചോദനം യാതൊരു മാറ്റവുമില്ലാതെ q ആയി നിലനിൽക്കുന്നു.
അതുപോലെ ഡയഗ്രം 2.39 ൽ കൊടുത്ത Rectangular hyperbola പോലെയുള്ള ചോദന വക്രത്തിലെ ഏതൊരു ബിന്ദുവിലെയും ഇലാസ്തികത ഏകാത്മക ഇലാസ്തിക ചോദനമായിരിക്കും.

Diagram 2.39

ചോദനത്തിന്റെ വില ഇലാസ്തികതയെ നിർണ്ണയിക്കുന്ന ഘടകങ്ങൾ ( Factors determin ing price elasticity of demand )
ചോദനത്തിന്റെ വില ഇലാസ്തികതയെ ഒരു പാട് ഘടകങ്ങൾ സ്വാധീനിക്കുന്നുണ്ട്. അവ ചുരുക്കി വിവരിക്കാം.

1. സാധനത്തിന്റെ പ്രകൃതം ( Nature of goods )
ഒരു സാധനത്തിന്റെ ഇലാസ്തികത , അതൊരു അവശ്യവസ്തുവാണോ ആഡംബരവസ്തുവാണോ അഥവാ സുഖഭോഗവസ്തുവാണോ എന്നിവയെ ആശ്രയിച്ചിരിക്കുന്നു. അവശ്യവസ്തുവാണെങ്കിൽ ഇലാസ്തികത കുറഞ്ഞതായിരിക്കും. ആഡംബര വസ്തുക്കളാണെങ്കിൽ ഉയർന്ന ഇലാസ്തിക ചോദനമായിരിക്കും.

2. പ്രതിസ്ഥാപന വസ്തുക്കളുടെ ലഭ്യത ( Availability of substitutes )
പ്രതിസ്ഥാപനവസ്തുക്കളുടെ ചോദനം ഇലാസ്തിക ചോദനമായിരിക്കും. എന്നാൽ പ്രതിസ്ഥാപന വസ്തുക്കളല്ലാത്തവയുടെ ചോദനം ഇലാസ്തികമല്ലാത്ത ചോദനമായിരിക്കും.

3. സാധനത്തിനുപയോഗിക്കുന്ന വരുമാനത്തിന്റെ അനുപാതം ( Proportion of the income spent on the good )
ചില സാധനങ്ങൾക്കുവേണ്ടി ഉപഭോക്താക്കൾ തങ്ങളുടെ വരുമാനത്തിന്റെ ചെറിയ ഭാഗമേ ഉപയോഗിക്കാറുള്ളൂ. ഉദാഹരണം , ഉപ്പ് , തീപ്പെട്ടി മുതലായവ. ഇത്തരം സാധനങ്ങളുടെ ഇലാസ്തിക ചോദനം കുറവായിരിക്കും.

4. ഉപഭോക്താവിന്റെ വരുമാനം ( Income of the consumer )
ഉയർന്ന വരുമാനമുള്ള സമ്പന്നരെ സംബന്ധിച്ചിടത്തോളം അവർ ഉപയോഗിക്കുന്ന മിക്ക സാധനങ്ങളുടെയും ഇലാസ്തിക ചോദനം കുറവായിരിക്കും. എന്നാൽ ദരിദ്രരുപയോഗിക്കുന്ന സാധനങ്ങളുടെ ഇലാസ്തിക ചോദനം ഉയർന്നതായിരിക്കും.

5. സാധനങ്ങളുടെ വില ( Price of goods )
വില കുറഞ്ഞ സാധനങ്ങളുടെ ഇലാസ്തിക ചോദനം കുറവും വില കൂടിയ സാധനങ്ങളുടെ ഇലാസ്തിക ചോദനം കൂടിയും ഇരിക്കും.

6. സമയദൈർഘ്യം ( Time period )
ഹ്രസ്വകാലത്തേക്കാളും ദീർഘകാലത്തേക്ക് ഇലാസ്തികത കൂടുതലാണ്. ഉപഭോക്താക്കൾക്ക് ദീർഘകാലയളവിൽ വില കുറഞ്ഞ പ്രതിസ്ഥാപന വസ്തുക്കളിലേക്ക് മാറാൻ കഴിയുന്നത് ഉപഭോഗം ക്രമീകരിക്കാൻ കഴിയുന്നതുകൊണ്ടാണ്.

Table 2.1
x₁	x₂ = 6 – 2x₁	ഉപഭോഗബണ്ടിലുകള്‍
0	x₂ = 6 – 2 × 0 = 6	(0, 6)
1	x₂ = 6 – 2 × 1 = 4	(1, 4)
2	x₂ = 6 – 2 × 2 = 2	(2, 2)
3	x₂ = 6 – 2 × 3 = 0	(3, 0)

Table 2.2
ബണ്ടിലുകൾ	റാങ്കിങ്
(2, 2)	I
(1, 3), (3, 1)	II
(1, 2), (2, 1)	III
(1, 1)	IV
(0, 1), (0, 2), (0, 3), (0, 4), (1, 0), (2, 0), (3, 0), (4, 0)	V

Table 2.3
മിശ്രണം	(സാധനം 2x₁)	സാധനം 1 (x₂)	\( \mathbf {MRS_{x_{1}x_{2}} \,= \,\frac{Δx_2}{Δx_1}} \)
a	11	1	–
b	7	2	1:4
c	4	3	1:3
d	2	4	1:2
e	1	5	1:1

Table 2.4
രണ്ട് സാധനങ്ങളുടെ ബണ്ടിലുകൾ	ഉപയുക്തത പ്രാതിനിധ്യം
(2, 2)	40 units
(1, 3), (3, 1), 0, 4), (4, 0)	35 units
(1, 2), (2, 1), (0, 3), (3; 0)	28 units
(0, 2), (2, 0), (1, 1)	20 units
(0, 0), (0, 1), (1, 0)	10 units

Table 2.5
വില (P)	ചോദനം (q)	കാണുന്ന രീതി. q = 10 – 2P
0	10	q = 10 – 2 × 0 = 10 – 0 = 10
1	8	q = 10 – 2 × 1 = 10 – 2 = 8
2	6	q = 10 – 2 × 2 = 10 – 4 = 6
3	4	q = 10 – 2 × 3 = 10 – 6 = 4
4	2	q = 10 – 2 × 4 = 10 – 8 = 2
5	0	q = 10 – 2 × 5 = 10 – 10 = 0

Table – Market Demand
ഉപഭോക്താവ് A (2.6)	ഉപഭോക്താവ് B (2.7)	കമ്പോള ചോദനം (2.8) (ചോദനം A + ചോദനം B)
വില	ചോദനം	വില	ചോദനം	Price	Demand
10	5	10	7	10	12
20	4	20	6	20	10
30	3	30	5	30	8
40	2	40	4	40	6

Table 2.9 ചെലവു രീതി
വില (P)	ചോദനത്തിന്റെ അളവ് (q)	ചെലവ്	ഇലാസ്തികത
10	5	50	e > 1
15	3	45
10	6	60	e = 1
15	4	60
10	7	70	e < 1
15	6	90

ഉപഭോക്തൃ പെരുമാറ്റ സിദ്ധാന്തങ്ങൾ

കാർഡിനൽ യൂട്ടിലിറ്റി സമീപനം – ആൽഫ്രഡ് മാർഷൽ

ഓർഡിനൽ സമീപനം – ജെ.ആര്‍. ഹിക്‌സ്‌

റിവീൽഡ് പ്രിഫറൻസ് സമീപനം – പോള്‍ എ. സാമുവെല്‍സണ്‍

ഉപഭോഗബണ്ടില്‍ ( Consumption Bundle)

ഉപഭോക്താവിന്റെ ബജറ്റ്‌( Consumer’s Budget)

ബജറ്റ്‌ സെറ്റ്‌ (Budget Set)

ബജറ്റ്‌ പരിധി (Budget Constraint)

ബജറ്റ്‌ ലൈന്‍ (Budget Set)

വെര്‍ട്ടിക്കല്‍ ഹൊറിസോണ്ടല്‍ ഇന്റർസെപ്റ്റുകളുടെ അര്‍ത്ഥവും, കണ്ടുപിടിക്കുന്ന വിധവും.

വെര്‍ട്ടിക്കല്‍ ഇന്റെർസെപ്റ്റ് .

ഹൊറിസോണ്ടല്‍ ഇന്റര്‍സെപ്റ്റ്‌.

ബജറ്റ്‌ ലൈനിന്റെ ചരിവ്‌ കണ്ടെത്തുന്ന വിധം

വില അനുപാതവും ബജറ്റ്‌ ലൈനിന്റെ ചരിവും.(Price Ratio and Slope of the Budget Line)

ബജറ്റ് ലൈനിലും മുകളിലും താഴെയുമുള്ള ബിന്ദുക്കൾ ( Points on , above and below the Budget Line )

ബജറ്റ് സെറ്റിലെ മാറ്റങ്ങൾ ( Changes in Budget Set )

വരുമാനം വർദ്ധിച്ചാൽ :

വരുമാനം കുറഞ്ഞാൽ :

വിലയിലുണ്ടാകുന്ന മാറ്റം ( Changes in Price )

സാധനം 1 ന്റെ വില വർധിച്ചാൽ :

സാധനം 1 ന്റെ വില കുറഞ്ഞാൽ :

സാധനം 2 ന്റെ വിലയിൽ മാറ്റം :

സാധനം 2 ന്റെ വില വർധിച്ചാൽ :

സാധനം 2 ന്റെ വില കുറഞ്ഞാൽ :

ഉപഭോക്താവിന്റെ മുൻഗണനകൾ ( Preferences of the Consumer )

മൊണോടോണിക് പ്രിഫറൻസ് ( Monotonic Preferences )

രണ്ട് സാധനങ്ങൾക്കിടയിലെ പ്രതിസ്ഥാപനം ( Substitution between two goods )

പ്രതിസ്ഥാപന നിരക്ക് ( Rate of Substitutlon )

കുറഞ്ഞുകൊണ്ടിരിക്കുന്ന പ്രതിസ്ഥാപന നിരക്ക് ( Diminishing Rate of Substitution )

സീമാന്ത പ്രതിസ്ഥാപന നിരക്ക് ( Marginal Rate of Substitution- MRS )

നിസംഗതാവക്രം അഥവാ ഉദാസീനതാവക്രം ( Indifference Curve )

പ്രതിസ്ഥാപന നിരക്കും നിസംഗതാവക്രത്തിന്റെ ചെരിവും

അപചയ സീമാന്ത പ്രതിസ്ഥാപന നിരക്ക് ( Diminishing Marginal Rate of Sub stitution – DMRS )

നിസംഗതാഭൂപടം ( Indifference Map )

1. നിസ്സംഗത വക്രങ്ങൾ ഇടത്തുനിന്ന് വലത്തോട്ട് താഴേക്ക് ചരിഞ്ഞുകിടക്കുന്നു.

2. നിസംഗതാവക്രം ഉന്മധ്യമാണ്:

3. ഉയർന്ന തലത്തിലുള്ള നിസംഗതാവക്രങ്ങൾ ഉയർന്ന സംതൃപ്തിയെ പ്രതിനിധാനം ചെയ്യുന്നു:

4. നിസംഗതാവക്രങ്ങൾ ഒരിക്കലും പരസ്പരം ഛേദിദിക്കില്ല:

ഉപയുക്തതാ ധർമ്മം (Utility Function)

ഉപഭോക്താവിന്റെ സന്തുലിതാവസ്ഥ ( Consumer’s Equilibrium )

ചോദനം ( Demand )

ഒരു ചരക്കിനുള്ള ചോദനം ( Demand for a Commodity )

വ്യക്തിഗത ചോദനം ( Individual Demand )

ചോദന ധർമ്മം ( Demand Function )

q = f(P, Pr, M , T

q = d(P)

ചോദന നിയമം ( Law of Demand )

ചോദന വക്രം ( Demand Curve )

വില കുറയുമ്പോൾ ചോദനം കൂടുന്നതെന്തുകൊണ്ട് ? അല്ലെങ്കിൽ എന്തുകൊണ്ടാണ് ചോദന വക്രം താഴോട്ട് ചെരിഞ്ഞിറങ്ങുന്നത് ?

വില പ്രഭാവം ( Price effect )

പ്രതിസ്ഥാപന പ്രഭാവം ( Substitution effect )

വരുമാന പ്രഭാവം ( Income effect )

രേഖീയ ചോദനം ( Linear Demand )

ഒരു സാധനത്തിന്റെ ചോദനത്തെ നിർണ്ണയിക്കുന്ന ഘടകങ്ങൾ

ചോദനത്തിലെ മാറ്റങ്ങൾ ( Changes in Demand )

1. ചോദന വക്രത്തിലൂടെയുള്ള മാറ്റം ( Movement along the demand curve ) :

2. ചോദന വക്രത്തിന്റെ മാറ്റം ( Shift of demand curve ) :

കമ്പോള ചോദനം ( Market Demand )

കമ്പോള ചോദന വക്രം ( Market Demand Curve )

രണ്ട് രേഖീയ ചോദന വക്രങ്ങളുടെ കൂട്ടൽ ( Adding up of two Linear Demand Curves )

ചോദനത്തിന്റെ വില ഇലാസ്തികത ( Price Elasticity of Demand )

വില ഇലാസ്തികതയുടെ തോതുകൾ അഥവാ തീവ്രതകൾ ( Degree of Price Elasticity )

( 1 ) ഇലാസ്തിക ചോദനം ( Elastic demand )

( 2 ) ഏകാത്മക ഇലാസ്തിക ചോദനം ( Unitary elastic demand )

( 3 ) ഇലാസ്തികമല്ലാത്ത ചോദനം ( Inelastic demand )

( 4 ) പൂർണ്ണ ഇലാസ്തിക ചോദനം ( Perfectly elastic demand )

( 5 ) പൂർണ്ണ ഇലാസ്തികമല്ലാത്ത ചോദനം ( Perfectly inelastic demand )

വില ഇലാസ്തികത അളക്കുന്ന രീതികൾ ( Methods of measuring price elasticity of demand )

( 1 ) ശതമാന രീതി ( Percentage method )

( 2 ) ഒരു രേഖീയ ചോദന വക്രത്തിലെ വിവിധ ബിന്ദുക്കളിലെ ഇലാസ്തികത നിർണ്ണയിക്കുന്ന വിധം ( Measurement of elasticity along a linear demand curve )

ജ്യാമിതീയ രീതിയനുസരിച്ച് ഇലാസ്തികത കാണുന്ന വിധം ( Geometric measure of elasticity )

( 3 ) ചെലവു രീതി ( Expenditure method )

സ്ഥിര ഇലാസ്തിക ചോദന വക്രങ്ങൾ ( Constant elasticity demand curves )

ചോദനത്തിന്റെ വില ഇലാസ്തികതയെ നിർണ്ണയിക്കുന്ന ഘടകങ്ങൾ ( Factors determin ing price elasticity of demand )

1. സാധനത്തിന്റെ പ്രകൃതം ( Nature of goods )

2. പ്രതിസ്ഥാപന വസ്തുക്കളുടെ ലഭ്യത ( Availability of substitutes )

3. സാധനത്തിനുപയോഗിക്കുന്ന വരുമാനത്തിന്റെ അനുപാതം ( Proportion of the income spent on the good )

4. ഉപഭോക്താവിന്റെ വരുമാനം ( Income of the consumer )

5. സാധനങ്ങളുടെ വില ( Price of goods )

6. സമയദൈർഘ്യം ( Time period )

q = f(P, P_r, M , T