Chapter 4 :-
പൂർണ്ണമത്സര കമ്പോളത്തിലെ ഉല്പാദക യൂണിറ്റിനെ കുറിച്ചുള്ള സിദ്ധാന്തം
ഒരു സ്ഥാപനത്തിന്റെ ഉല്പാദന ധർമം,ചെലവ് ധർമം എന്നിവയെക്കുറിച്ചാണ് കഴിഞ്ഞ അധ്യായത്തിൽ നമ്മൾ പഠിച്ചത്. സമ്പൂർണ കിടമത്സര കമ്പോളത്തിലെ ഒരു സ്ഥാപനത്തിന്റെ ഉല്പന്നത്തിന്റെ വില, ഉല്പാദനത്തിന്റെ അളവ് നിർണയം, സ്ഥാപനത്തിന്റെ സന്തുലിതാവസ്ഥ, പ്രദാനം, പ്രദാനത്തിന്റെ വില ഇലാസ്തികത തുടങ്ങിയവയാണ് നാം ഈ അധ്യായത്തിൽ പഠിക്കാൻ പോകുന്നത്.
കമ്പോളം (Market)
ഒരു സാധാരണ വ്യക്തിയെ സംബന്ധിച്ചിടത്തോളം കമ്പോളം എന്നു പറയുന്നത് സാധനങ്ങൾ വാങ്ങുകയും വിൽക്കുകയും ചെയ്യുന്ന ഒരു ഭൂപ്രദേശമാണ്. എന്നാൽ സാമ്പത്തിക ശാസ്ത്രത്തിൽ കൂടുതൽ വിശാലമായ അർത്ഥത്തിലാണ് ഈ പദം ഉപയോഗിക്കുന്നത്. സാധനങ്ങളും സേവനങ്ങളും വാങ്ങുന്നതിനും വില്ക്കുന്നതിനും ക്രേതാക്കളും (buyers) വിക്രേതാക്കളും (sellers) പരസ്പരം സമ്പർക്കത്തിൽ ഏർപ്പെടുന്ന സംവിധാനമാണ് കമ്പോളം.
കമ്പോള രൂപങ്ങൾ (Forms of Market)
കമ്പോളത്തെ താഴെ കൊടുത്തിരിക്കുന്ന വിധത്തിൽ തരംതിരിച്ചിരിക്കുന്നു.
- 1. സമ്പൂർണ കിടമത്സരം
- 2. അപൂർണ കിടമത്സരം
- (a) കുത്തകാധിഷ്ഠിതമായ മത്സരം
- (b) അാധീശത്വ വ്യാപാരം
- 3. കുത്തക
സമ്പൂർണ കിടമത്സരം (Perfect Competition)
പ്രായോഗിക തലത്തിൽ അത്യപൂർവമായി കാണുന്ന ഒരു കമ്പോളമാണ് സമ്പൂർണ കിടമത്സരം അഥവാ പരിപൂർണ കിടമത്സരം. ദൈനംദിന ജീവിതത്തിൽ ഉപയോഗിക്കുന്നതിന് വിപരീത അർത്ഥത്തിലാണ് സമ്പൂർണ കിടമത്സരം എന്ന പദം സാമ്പത്തിക ശാസ്ത്രത്തിൽ ഉപയോഗിക്കുന്നത്. ഉല്പാദന സ്ഥാപനങ്ങൾ തമ്മിൽ മത്സരം ഇല്ലാത്ത ഒരു കമ്പോളമാണിത്. സ്ഥാപനങ്ങൾക്കിടയിൽ എതിരാളികൾ ഇല്ലാത്ത ഒരു കമ്പോള സിദ്ധാന്തമാണ് പൂർണ കിടമത്സരം എന്നതുകൊണ്ട് സൂചിപ്പിക്കുന്നത്.
ഏകജാതീയ (homogeneous) ഉല്പന്നങ്ങൾ കൈകാര്യം ചെയ്യുന്ന ധാരാളം ക്രേതാക്കളും വിക്രേതാക്കളും ഉള്ള ഒരു കമ്പോള സംവിധാനത്തെയാണ് സമ്പൂർണ കിടമത്സര കമ്പോളം എന്നു പറയുന്നത്. സമ്പൂർണ കിടമത്സര കമ്പോളത്തിന് താഴെ പറയുന്ന സവിശേഷതകൾ ഉണ്ടായിരിക്കും:
- 1. വളരെയധികം ക്രേതാക്കളും വിക്രേതാക്കളും ഉണ്ടായിരിക്കും.
- 2. എല്ലാ ഉല്പാദക സ്ഥാപനങ്ങളും ഉല്പാദിപ്പിക്കുന്ന സാധനം ഏകജാതീയമായിരിക്കും.
- 3. സ്ഥാപനങ്ങൾക്ക് കമ്പോളത്തിലേക്ക് പ്രവേശിക്കാനും ഉല്പാദനം നിർത്തി പുറത്തുപോകാനും പൂർർണസ്വാതന്ത്ര്യം ഉണ്ടായിരിക്കും.
- 4. കമ്പോള സ്ഥിതിയെക്കുറിച്ച് പൂർണ അറിവ് ഉണ്ടായിരിക്കും.
- 5. ഉല്പാദനഘടകങ്ങൾക്കും സാധനങ്ങൾക്കും പൂർണ ചലനസ്വാതന്ത്ര്യമുണ്ടായിരിക്കും.
- 6. ഗതാഗതച്ചെലവ് ഉണ്ടായിരിക്കില്ല.
- 7. സാധനങ്ങൾക്ക് സമാന വിലയായിരിക്കും.
- 8. സാധനങ്ങൾക്ക് പൂർണ ഇലാസ്തിക ചോദനമായിരിക്കും.
- 9. ഗവൺമെന്റ് നിയന്ത്രണം ഇല്ല.
- 10. വില്പന ചെലവില്ല.
സമ്പൂർണ കിടമത്സര കമ്പോളത്തിലെ ഒരു നിർണായക സവിശേഷതയാണ് ഈ കമ്പോളത്തിലുള്ള ഉല്പാദകർ ഉല്പാദിപ്പിക്കുന്ന ഉല്പന്നങ്ങൾ എല്ലാം ഒരേപോലെയുള്ള ഉല്പന്നങ്ങളാണ് എന്നത്. ഉല്പന്നങ്ങൾ തമ്മിൽ യാതൊരു വ്യത്യാസവുമില്ല. അവയുടെ നിറം, മണം, ഗുണം, വലിപ്പം എന്നിവയെല്ലാം ഒരേ പോലെയായിരിക്കും. രണ്ടാമത്തെ സവിശേഷതയനുസരിച്ച് സമ്പൂർണ കിടമത്സര കമ്പോളത്തിലെ ഓരോ ക്രേതാവും (വാങ്ങുന്നവൻ) വിക്രേതാവും (വില്ക്കുന്നവൻ) “വില സ്വീകരിക്കുന്നവൻ (Price-taker)” ആയിരിക്കും. അതായത്, കമ്പോളത്തിൽ നിലവിലുള്ള വില ക്രേതാക്കളും വിക്രേതാക്കളും സ്വീകരിക്കേണ്ടി വരുന്നു. ഉല്പാദകനോ ഉപഭോക്താവിനോ വിലയെ സ്വാധീനിക്കാൻ കഴിയില്ല. വില സ്വീകരിക്കുന്നവൻ എന്നതുകൊണ്ട് രണ്ട് കാര്യങ്ങൾ സൂചിപ്പിക്കുന്നു.
ഏതെങ്കിലും ഒരു ഉല്പാദകൻ കമ്പോളവിലയേക്കാൾ ഉയർന്ന വില നിശ്ചയിച്ചാൽ ആ ഉല്പാദകന് ഉപഭോക്താക്കളെ നഷ്ടമാകും. അയാൾ ഉല്പാദിപ്പിക്കുന്ന സാധനത്തിന് ചോദനം ഇല്ലാതെയാവുകയും ഉല്പാദനം നിർത്തിപ്പോകേണ്ടി വരികയും ചെയ്യും. ഉല്പാദകന് “സാധാരണ ലാഭം (Normal Profit)” മാത്രം ലഭിക്കുന്നതു കൊണ്ട് കമ്പോളവിലയേക്കാൾ കുറഞ്ഞ വിലയ്ക്ക് സാധനം വില്ക്കാൻ അദ്ദേഹം തയ്യാറാവുകയില്ല. ഒരു ഉപഭോക്താവിനെ സംബന്ധിച്ചിടത്തോളം ഏറ്റവും കുറഞ്ഞ വിലയ്ക്ക് സാധനങ്ങൾ വാങ്ങാൻ അയാൾ ആഗ്രഹിക്കുന്നു. കമ്പോളവിലയേക്കാൾ കുറഞ്ഞ വിലയ്ക്ക് ഉപഭോക്താവിന് സാധനം ലഭ്യമാകുകയില്ല. എന്തുകൊണ്ടെന്നാൽ കമ്പോളവിലയേക്കാൾ കുറഞ്ഞ വിലയ്ക്ക് സാധനം വില്ക്കാൻ ഉല്പാദകൻ തയ്യാറാകുകയില്ല. ഉപഭോക്താവിന് കമ്പോള വിലയ്ക്ക് എത്ര അളവ് സാധനവും ലഭ്യമാകും.
ചുരുക്കത്തിൽ സമ്പൂർണ കിടമത്സര കമ്പോളത്തിൽ സാധനത്തിന്റെ വില എപ്പോഴും കമ്പോളവിലയ്ക്ക് തുല്യമായിരിക്കും. ഈ വിലയ്ക്ക് ഒരു സാധനത്തിന്റെ എത്ര അളവ് വേണമെങ്കിലും വില്ക്കുവാനും വാങ്ങുവാനും കഴിയും. അതുകൊണ്ട്, ഉല്പാദകൻ വില്ക്കുന്ന ഉല്പന്നത്തിന്റെ ഓരോ യൂണിറ്റിന്റെയും വില സ്ഥിരമായിരിക്കും. കമ്പോളവിലയ്ക്ക് ഉല്പാദകന് ഏതളവ് സാധനം വില്ക്കുവാനും ഉപഭോക്താവിന് ഏതളവ് സാധനം വാങ്ങുവാനും കഴിയുന്നതു കൊണ്ട് സമ്പൂർണ കിടമത്സര കമ്പോളത്തിലെ ഓരോ ഉല്പാദകനെയും ഓരോ ഉപഭോക്താക്കളെയും വില സ്വീകരിക്കുന്നവൻ എന്നു വിളിക്കുന്നു.
വരുമാനം (Revenue)
ഒരു ഉല്പാദകൻ ഉല്പാദിപ്പിച്ച ഉല്പന്നം കമ്പോളത്തിൽ വില്ക്കുമ്പോൾ ലഭിക്കുന്ന വരവിനെ വരുമാനം അഥവാ വിറ്റുവരവ് എന്നു പറയുന്നു. ഒരു ഉല്പാദക യൂണിറ്റ് ഉല്പാദിപ്പിക്കുന്ന സാധനങ്ങൾ വില്ക്കുമ്പോൾ കിട്ടുന്ന ആകെ തുകയെ മൊത്തം വരുമാനം (Total Revenue – TR) എന്നു പറയുന്നു. കമ്പോളവിലയെ (p) ഉല്പന്നത്തിന്റെ അളവുകൊണ്ട് (q) ഗുണിച്ചാണ് മൊത്തം വരുമാനം കാണുന്നത്. അതായത്, TR = p × q
Eg 4.1: സമ്പൂർണ കിടമത്സര കമ്പോളത്തിൽ ഉല്പന്നത്തിന്റെ വില സ്ഥിരമാണ്. ഉദാഹരണമായി, പട്ടിക 4.1 ൽ ഉല്പന്നത്തിന്റെ വില 10 യും ഉല്പന്നത്തിന്റെ വിവിധ അളവും കൊടുത്തിരിക്കുന്നു. വിലയെ ഉല്പന്നത്തിന്റെ അളവുകൊണ്ട് ഗുണിച്ച് മൊത്തം വരുമാനം കണക്കാക്കിയിരിക്കുന്നത് നോക്കുക.
| Table 4.1 മൊത്തം വരുമാനം | ||
|---|---|---|
| വില (P) | ഉല്പന്നത്തിന്റെ അളവ് (Q) | മൊത്തം വരുമാനം = P × Q |
| 10 | 0 | 0 |
| 10 | 1 | 10 |
| 10 | 2 | 20 |
| 10 | 3 | 30 |
| 10 | 4 | 40 |
| 10 | 5 | 50 |
| 10 | 6 | 60 |
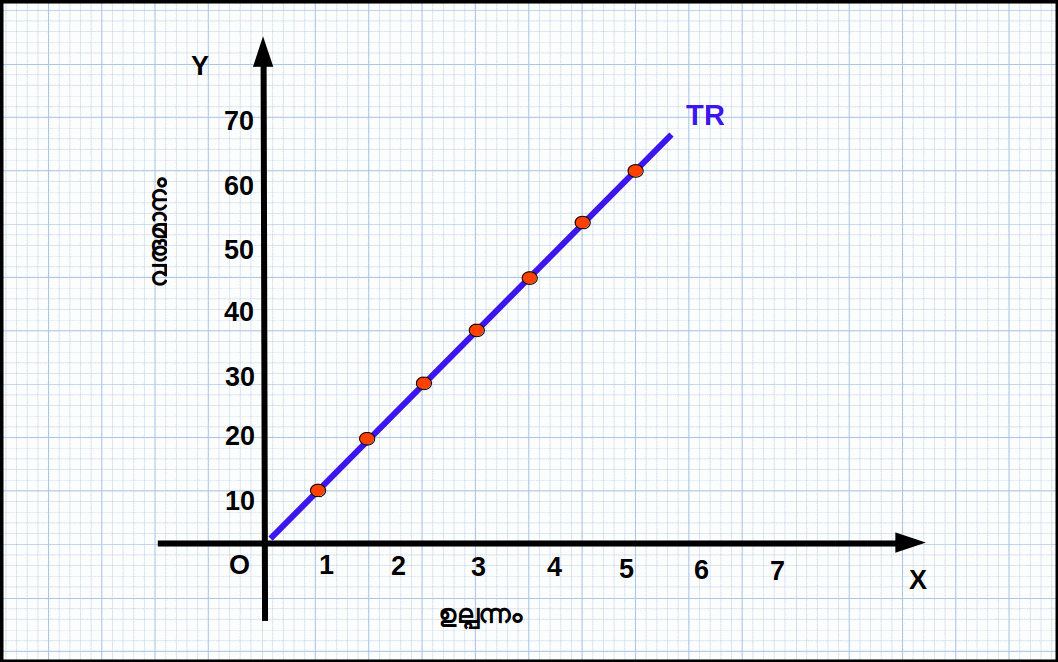
- 1. പൂജ്യം ഉല്പന്നത്തിൽ മൊത്തം വരുമാനവും പൂജ്യമായിരിക്കും. അതുകൊണ്ട് TR വക്രം O എന്ന ബിന്ദുവിൽ കൂടി കടന്നുപോകുന്നു.
- 2. ഉല്പന്നത്തിന്റെ അളവ് വർധിക്കുന്നതിനനു സരിച്ച് TR ഉയരുന്നു. കൂടാതെ TR വക്രം മുകളിലേക്ക് ഉയരുന്ന ഒരു നേർരേഖയാണ്.
- 3. TR വക്രത്തിന്റെ ചരിവ് വിലയ്ക്ക് തുല്യമാണ്. ഉല്പന്നം 1 യൂണിറ്റ് മാറുമ്പോൾ മൊത്തം വരുമാനത്തിലുള്ള മാറ്റം 10 ആണ്.
വില രേഖ (Price Line)
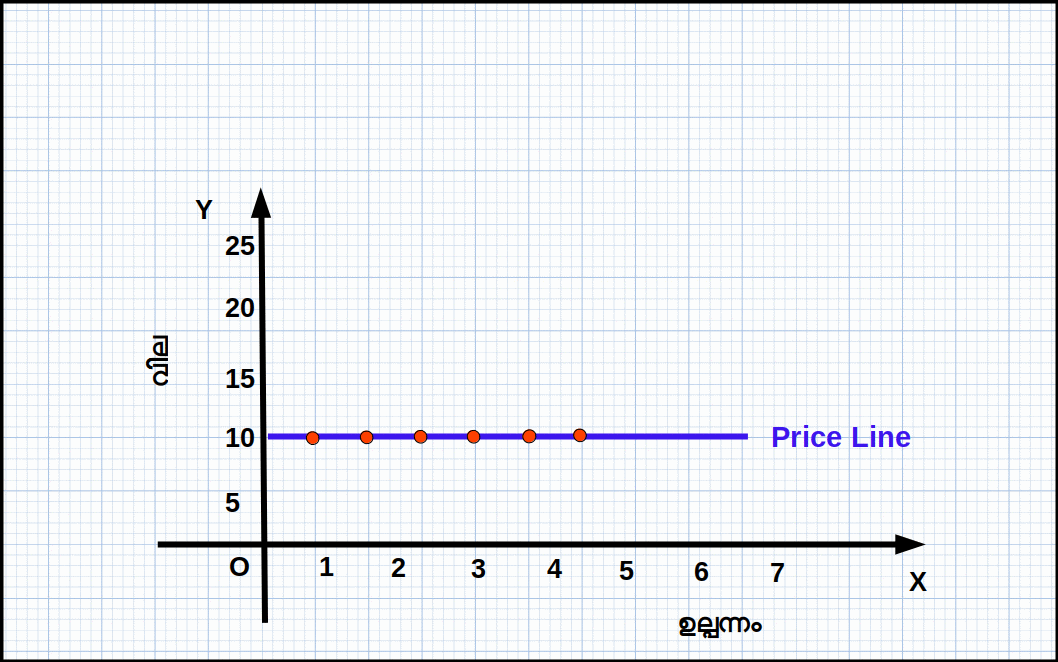
വിലയും ഉല്പന്നവും തമ്മിലുള്ള ബന്ധത്തെ വിലരേഖ സൂചിപ്പിക്കുന്നു. സമ്പൂർണ കിടമത്സര കമ്പോളത്തിൽ ഒരു സ്ഥാപനത്തിന്റെ ഉല്പന്നം വിലയെ ആശ്രയിച്ചല്ല നിലനിൽക്കുന്നത്. ഇത് അർത്ഥമാക്കുന്നത് നിശ്ചിത വിലയ്ക്ക് എത്ര യൂണിറ്റ് ഉല്പന്നം വേണമെങ്കിലും വില്ക്കാൻ സാധ്യമാണെന്നാണ്. പട്ടിക 4.1 ൽ ഉല്പന്നത്തിന്റെ വില 10 ആണ്. ഉല്പന്നത്തിന്റെ അളവ് വർധിക്കുന്നതിനനുസരിച്ച് വിലയിൽ മാറ്റമില്ല. വിലയും ഉല്പന്നവും തമ്മിലുള്ള ബന്ധം കാണിക്കുന്ന രേഖയെയാണ് വില രേഖ എന്നു പറയുന്നത്.
Eg 4.2; വില y-അക്ഷത്തിലും ഉല്പന്നം x-അക്ഷത്തിലും അടയാളപ്പെടുത്തി വില ഉല്പന്ന സംയോഗങ്ങൾ ചേർത്ത് വരച്ചാൽ ഗ്രാഫ് 4.2 ൽ കാണുന്നതുപോലെ ഒരു ഹൊറിസോണ്ടൽ രേഖ ലഭിക്കുന്നു; ഇതാണ് വിലരേഖ. വിലരേഖ X-അക്ഷത്തിന് സമാന്തരമാണ്.
ശരാശരി വരുമാനം (Average Revenue – AR)
വിറ്റ ഉല്പന്നത്തിന്റെ ഓരോ യൂണിറ്റിൽ നിന്നുമുള്ള വരുമാനമാണ് ശരാശരി വരുമാനം. മൊത്തം വരുമാനത്തെ വിറ്റ ഉല്പന്നത്തിന്റെ അളവുകൊണ്ട് ഹരിച്ചാണ് ശരാശരി വരുമാനം കാണുന്നത്. ഗണിത രൂപത്തിൽ
\( \mathbf{AR \,=\, {\frac{TR}{q}} } \) = \( \mathbf{{\frac{pq}{q}} } \) = p
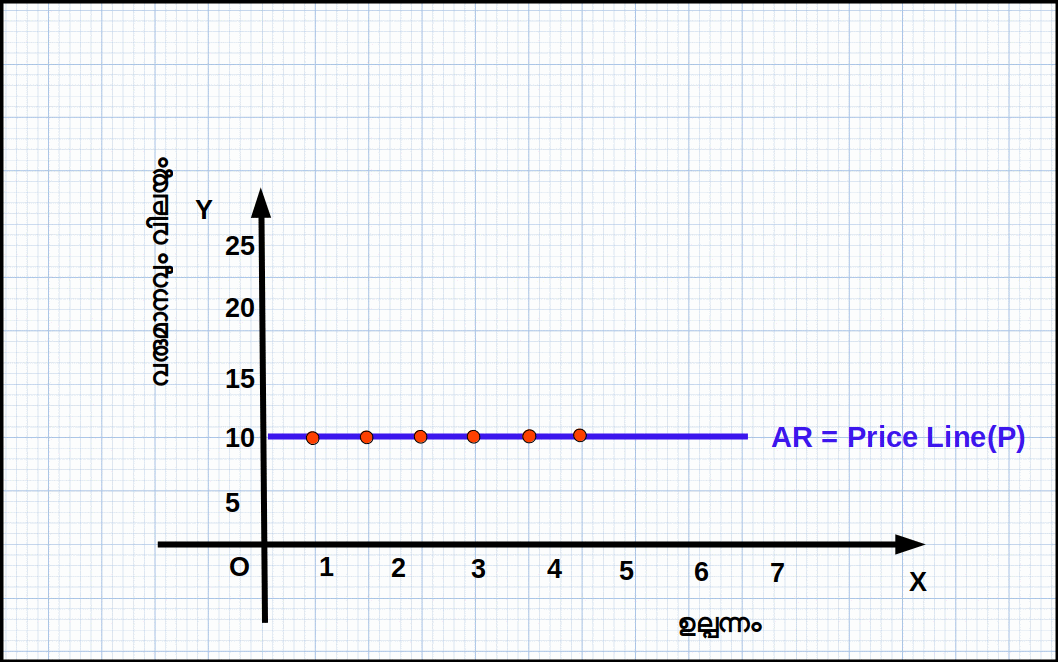
AR വിലയ്ക്ക് തുല്യമാണ്. അതുകൊണ്ട്, വിലരേഖയും AR വക്രവും ഒന്നുതന്നെയാണ്. ഈ രേഖയാണ് സമ്പൂർണ കിടമത്സര കമ്പോളത്തിലെ ചോദന വക്രം.
Eg 4.3: പട്ടിക 4.2 ൽ TR ഉം AR ഉം കൊടുത്തിരിക്കുന്നു. സാധനത്തിന്റെ ഒരു യൂണിറ്റിന്റെ വില 10 യാണ്.
| Table 4.2 ശരാശരി വരുമാനം | |||
|---|---|---|---|
| വില (P) | ഉല്പന്നം (Q) | മൊത്തം വരുമാനം (TR = P×Q) | ശരാശരി വരുമാനം (\(\mathbf{AR=\frac{TR}{Q}}\)) |
| 10 | 0 | 0 | 0 |
| 10 | 1 | 10 | 10÷1=10 |
| 10 | 2 | 20 | 20÷2=10 |
| 10 | 3 | 30 | 30÷3=10 |
| 10 | 4 | 40 | 40÷4=10 |
| 10 | 5 | 50 | 50÷5=10 |
| 10 | 6 | 60 | 60÷6=10 |
അതായത്, AR = P = 10. അതുകൊണ്ട് AR വക്രം വിലരേഖ തന്നെയാണ്.
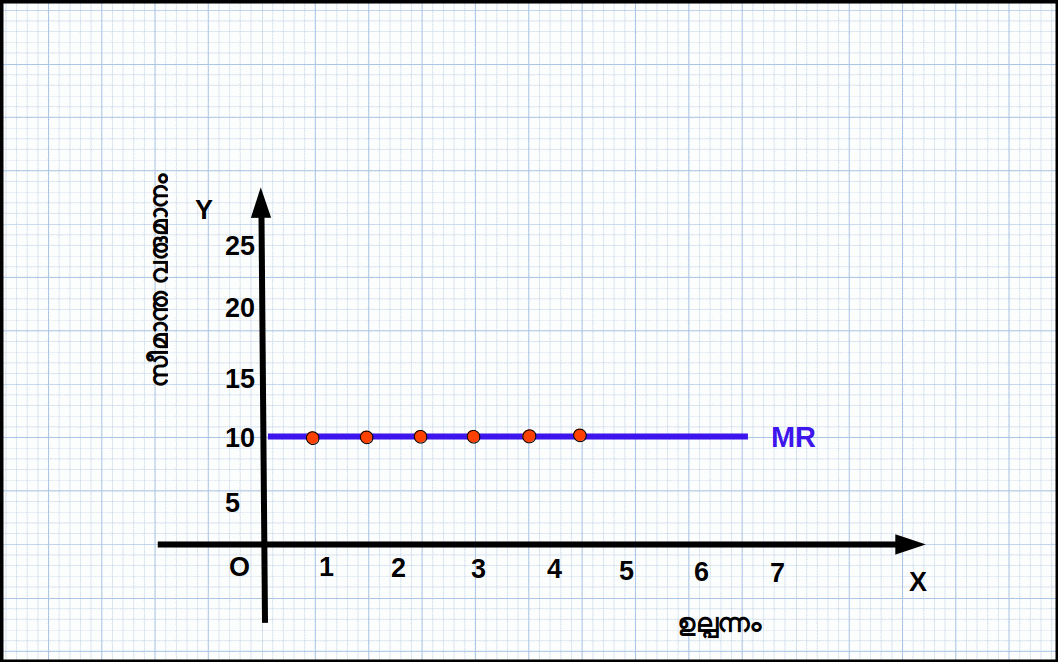
സീമാന്ത വരുമാനം (Marginal Revenue – MR)
ഉല്പന്നത്തിന്റെ ഒരു അധിക യൂണിറ്റ് വിൽക്കുന്നതു വഴി ലഭിക്കുന്ന അധിക വരുമാനമാണ് സീമാന്ത വരുമാനം. മൊത്തം വരുമാനത്തിലുള്ള മാറ്റമാണ് ഇത്. മൊത്തം വരുമാനത്തിന്റെ മാറ്റത്തിന്റെ നിരക്കാണ് സീമാന്ത വരുമാനം. ഒരു ഉല്പാദക യൂണിറ്റിന്റെ ഉല്പന്നത്തിന്റെ അളവ് q° ൽനിന്ന് (q° + 1) ആയി വർധിക്കുന്നുവെന്ന് കരുതുക. അപ്പോൾ,
MR = [(q° + 1) ഉല്പന്നത്തിൽ നിന്നുള്ള TR] – [q° ഉല്പന്നത്തിൽ നിന്നുള്ള TR]
വില p ആണെങ്കിൽ,
MR = [p(q° + 1)] – (pq°)
= pq° + p – pq° = p
വില സ്വീകരിക്കുന്ന ഒരു കമ്പോളത്തിൽ സീമാന്ത വരുമാനം വിലയ്ക്ക് തുല്യമാണ് (MR = P).
Marginal Revenue
(\(\mathbf{MR=\frac{ΔTR}{Δq}}\))
MRn = TRn – TRn – 1MRn = n യൂണിറ്റിലുള്ള MRTRn = n യൂണിറ്റ് വില്പനയിൽനിന്നുള്ള TRTRn – 1 = n – 1 യൂണിറ്റ് വില്പനയിൽനിന്നുള്ള TR
| Table 4.3 മൊത്തം വരുമാനവും സീമാന്ത വരുമാനവും | ||
|---|---|---|
| ഉല്പന്നം (Q) | മൊത്തം വരുമാനം (TR) | സീമാന്ത വരുമാനം (\(\mathbf{MR = \frac{ΔTR}{ΔQ}}\)) |
| 0 | 0 | – |
| 1 | 10 | 10 ÷ 1 = 10 |
| 2 | 20 | 10 ÷ 1 = 10 |
| 3 | 30 | 10 ÷ 1 = 10 |
| 4 | 40 | 10 ÷ 1 = 10 |
| 5 | 50 | 10 ÷ 1 = 10 |
| 6 | 60 | 10 ÷ 1 = 10 |
| Table 4.4 | ||
|---|---|---|
| വില | ഉല്പന്നം | |
| 2 | 0 | |
| 2 | 1 | |
| 2 | 2 | |
| 2 | 3 | |
| 2 | 4 | |
| 2 | 5 | |
- 1. TR, AR, MR എന്നിവ കാണുക.
- 2. TR, AR, MR എന്നിവ ഒരു ഗ്രാഫിൽ വരയ്ക്കുക.
- 3. ഓരോ വക്രത്തിന്റെയും സവിശേഷതകൾ വിവരിക്കുക.
-
Table 4.5 P q TR=P × q \(\mathbf{AR=\frac{TR}{q}}\) \(\mathbf{MR=\frac{ΔTR}{Δq}}\) 2 0 0 – – 2 1 2 2 2 2 2 4 2 2 2 3 6 2 2 2 4 8 2 2 2 5 10 2 2 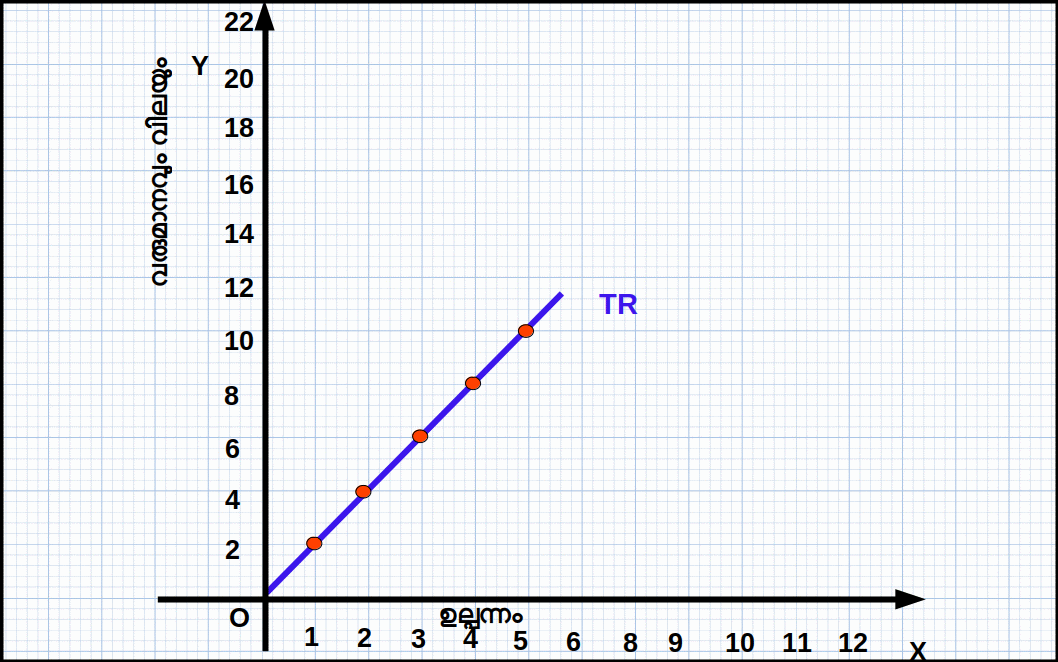 Diagram 4.5
Diagram 4.5- TR വക്രം മുകളിലേക്ക് ഉയരുന്ന ഒരു നേർരേഖയാണ്. TR പൂജ്യത്തിൽനിന്ന് തുടങ്ങി ഉല്പന്നം വർധിക്കുന്നതിന് ആനുപാതികമായി വർധിക്കുന്നു. TR രേഖയുടെ ചരിവ് \(\mathbf{MR=\frac{ΔTR}{Δq}}\) = 2 ആണ്. വിലരേഖയ്ക്ക് തുല്യമാണ് AR, MR രേഖകൾ. ഇവ പരസ്പരം ചേർന്നിരിക്കുന്നു. ഉല്പന്നത്തിന്റെ അളവ് മാറുന്നതിനനുസരിച്ച് ഇവയിൽ മാറ്റം വരുന്നില്ല. ഇവ x-അക്ഷത്തിന് സമാന്തരമാണ്. സമ്പൂർണ കിടമത്സരത്തിൽ P = AR = MR വക്രമാണ് ചോദന വക്രവും.
ലാഭം പരമാവധിയാക്കൽ (Profit Maximisation) ഓരോ ഉല്പാദകനും സാധനങ്ങളോ സേവന ങ്ങളോ ഉല്പാദിപ്പിക്കുകയും അവ കമ്പോളത്തിൽ വിറ്റഴിക്കുകയും ചെയ്യുന്നു. എല്ലാ ഉല്പാദക യൂണിറ്റി ന്റെയും പ്രധാന ലക്ഷ്യം തന്റെ ലാഭം പരമാവധിയാ ക്കുക എന്നതാണ്. ഉല്പന്നങ്ങൾ കമ്പോളത്തിൽ വിറ്റ് ഉല്പാദകന്റെ ലാഭം പരമാവധിയിൽ എത്തുന്ന അവസ്ഥയെ സന്തുലിതാവസ്ഥ (equilibrium) എന്നു പറയുന്നു. അതായത്, ഉല്പാദകന് ഉല്പന്നത്തിന്റെ അളവ് വർധിപ്പിക്കാനോ കുറയ്ക്കാനോ താല്പര്യമില്ലാത്ത സ്ഥിതിയാണ് സന്തുലിതാവസ്ഥ. ഒരു ഉല്പാദക യൂണിറ്റിന്റെ TR ഉം TC യും തമ്മിലുള്ള വ്യത്യാസമാണ് ലാഭം ( π – പൈ). അതായത്,
π = TR – TC
അപ്പോൾ, ഒരു സ്ഥാപനം സന്തുലിതാവസ്ഥയിൽ എത്തുന്നത് TR ഉം TC യും തമ്മിലുള്ള വ്യത്യാസം ഏറ്റവും കൂടിയിരിക്കുമ്പോഴാണ്. TR ഉം TC യും തമ്മിലുള്ള വ്യത്യാസം ഏറ്റവും കൂടിയിരിക്കുന്നത് താഴെ പറയുന്ന മൂന്ന് വ്യവസ്ഥകൾ പാലിക്കുമ്പോഴാണ്. അതായത്, ഒരു സ്ഥാപനം സന്തുലിതാവസ്ഥ പ്രാപിക്കണമെങ്കിൽ മൂന്ന് വ്യവസ്ഥകൾ പാലിക്കണം:
- 1. MC യും MR ഉം തുല്യമാകണം (MR=MC).
- 2. സീമാന്ത ചെലവ് കുറയാതെയിരിക്കണം. മറ്റൊരു വിധത്തിൽ പറഞ്ഞാൽ MC വക്രം MR വക്രത്തെ താഴെനിന്ന് ഖണ്ഡിക്കണം.
- 3. മൂന്നാമത്തെ വ്യവസ്ഥ:
- (a) ഹ്രസ്വകാലഘട്ട ത്തിൽ വില ശരാശരി വിഭേദക ചെലവിന് തുല്യമോ അതിനേക്കാൾ കൂടുതലോ ആയിരിക്കണം. P ≥ AVC.
- (b) ദീർഘകാലയളവിൽ വില ശരാശരി ചെലവിന് തുല്യമോ അതിനേക്കാൾ കൂടുതലോ ആയിരിക്കണം. P ≥ AC.
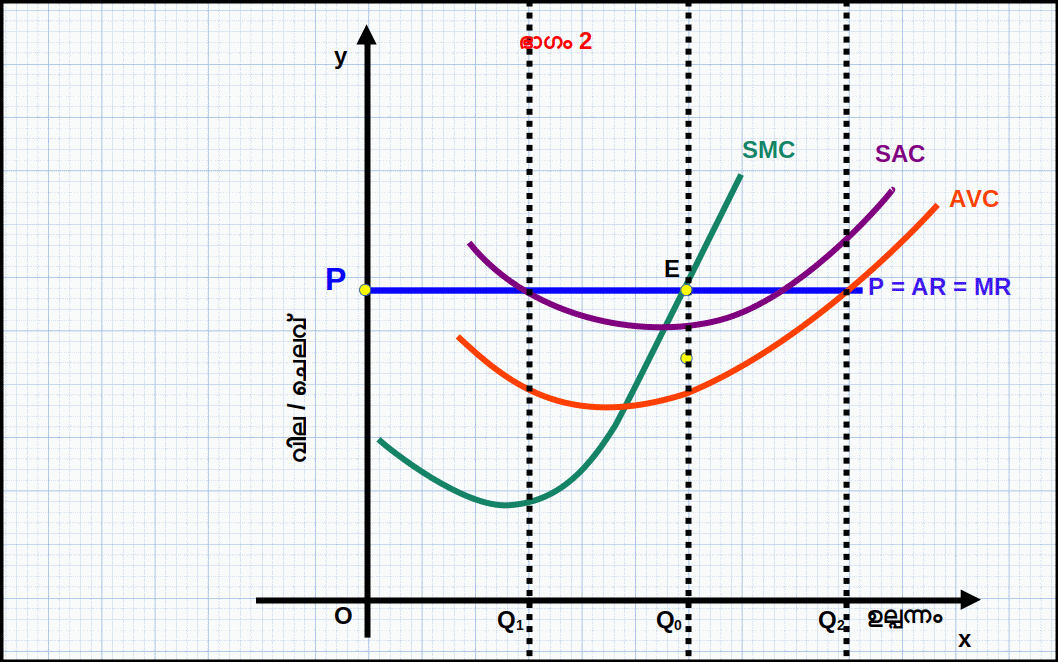
വ്യവസ്ഥ 1: വിലയും സീമാന്ത ചെലവും തുല്യമായിരിക്കണം എന്നതാണ് സമ്പൂർണ കിടമത്സര കമ്പോളത്തിലെ സന്തുലിതാവസ്ഥയുടെ ഒന്നാമത്തെ വ്യവസ്ഥ. വിലയും സീമാന്ത ചെലവും തുല്യമല്ലാതെ വരുമ്പോൾ രണ്ട് സ്ഥിതി ഉണ്ടാകുന്നു. (1) വില സീമാന്ത ചെലവിനേക്കാൾ കൂടിയിരിക്കുക (P > MC). (2) സീമാന്ത ചെലവ് വിലയേക്കാൾ കൂടിയിരിക്കുക (MC > P). ഈ രണ്ട് സ്ഥിതിയിലും ലാഭം പരമാവധിയിലാകുകയില്ല. ഈ രണ്ട് സ്ഥിതിയും നമുക്ക് ഒരു ഡയഗ്രത്തിന്റെ സഹായത്തോടെ വിശദമാക്കാം. സ്ഥിതി 1 സീമാന്ത ചെലവിനേക്കാൾ വില കൂടി യിരിക്കുന്നത് പരിഗണിക്കില്ല. ഡയഗ്രം 4.6 ൽ X-അക്ഷത്തിൽ ഉല്പന്നത്തിന്റെ അളവും y-അക്ഷത്തിൽ വിലയും സീമാന്ത ചെലവും രേഖപ്പെടുത്തിയിരിക്കുന്നു. P = MR = AR എന്നത് വിലരേഖയും MC എന്നത് സീമാന്ത ചെലവും വക്രവുമാണ്. MC വക്രം ഉല്പന്നത്തിന്റെ അളവ് വർധിക്കുന്നതിനനുസരിച്ച് ആദ്യം കുറയുകയും പിന്നീട് വർധിക്കുകയും ചെയ്യുന്നു.
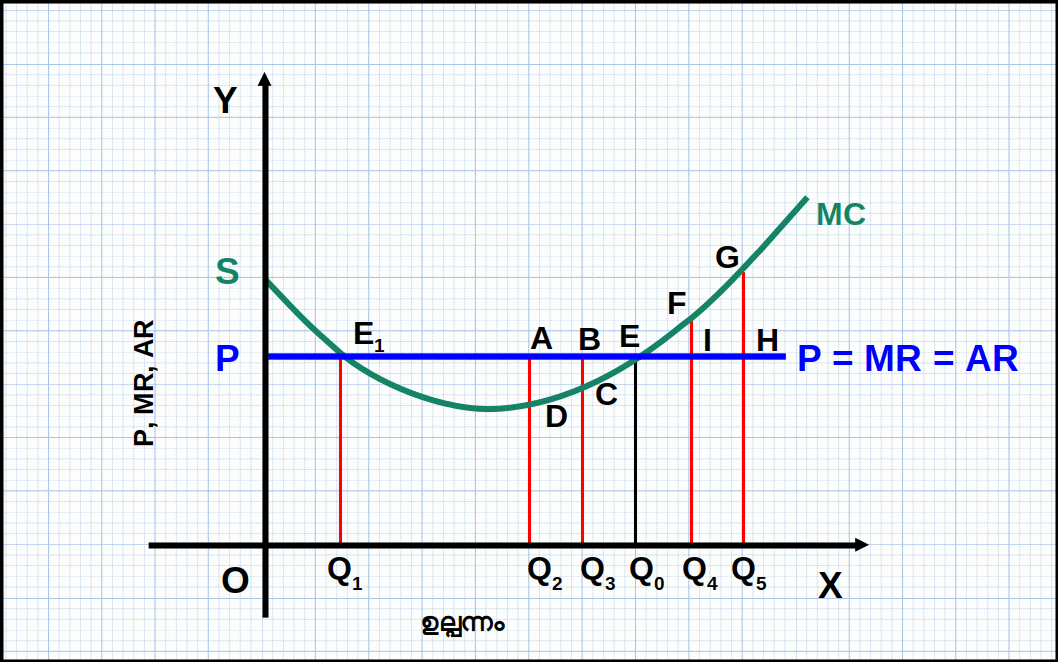
Q1 ന് മുമ്പുള്ള ഉല്പന്ന തലത്തിൽ MC വിലയേക്കാൾ കൂടിയിരിക്കുന്നതുകൊണ്ട് സ്ഥാപനത്തിന് നഷ്ടമാണ്. ഈ സാഹചര്യത്തിൽ ഉല്പന്നത്തിന്റെ അളവ് വർധിപ്പിച്ചുകൊണ്ട് സ്ഥാപനത്തിന് ലാഭം പരമാവധിയാക്കാൻ കഴിയും. E1 എന്ന ബിന്ദുവിൽ സീമാന്ത ചെലവും വിലയും തുല്യമാണ്. പക്ഷേ സ്ഥാപനത്തിന് നഷ്ടമാണ്.
വ്യവസ്ഥ 2: സന്തുലിത ഉല്പന്നത്തിൽ സീമാന്ത ചെലവ് കുറയാതെയിരിക്കണം എന്നതാണ് സമ്പൂർണ കിടമത്സര കമ്പോളത്തിന്റെ രണ്ടാമത്തെ വ്യവസ്ഥ. മറ്റൊരു വിധത്തിൽ പറഞ്ഞാൽ, ലാഭം പരമാവധിയാകുന്ന ഉല്പന്ന ബിന്ദുവിൽ MC വർധി ക്കണം. MC കുറഞ്ഞുകൊണ്ടിരിക്കുമ്പോൾ ഉല്പന്നത്തിന്റെ അളവ് വർധിപ്പിച്ചുകൊണ്ട് സ്ഥാപനത്തിന് ലാഭം പരമാവധിയാക്കാൻ കഴിയും. അതായത് MC ആദ്യം കുറഞ്ഞ് പിന്നെ വർധിക്കുമ്പോൾ വിലയ്ക്കു തുല്യമാകുന്ന ഉല്പന്നതലമാണ് സന്തുലിത ഉല്പന്നം. ഡയഗ്രം 4.6 ൽ ഉല്പന്നം Q0 ആയപ്പോൾ E എന്ന ബിന്ദുവിൽ വിലയും MC യും തുല്യമാണ്. ഇവിടെ MC വർധിക്കുന്ന അവസ്ഥയാണ്. അതുപോലെ Q1 ഉല്പന്ന തലത്തിൽ E1 എന്ന ബിന്ദുവിൽ വിലയും MC യും തുല്യമാണ്. പക്ഷേ MC കുറയുന്നു. അതുകൊണ്ട് Q1 സന്തുലിത ഉല്പന്നതലമല്ല. E എന്ന ബിന്ദുവിൽ MC വക്രം വിലരേഖയ താഴെനിന്നും മുകളിലേക്ക് ഖണ്ഡിക്കുന്നു.
വ്യവസ്ഥ 3: വ്യവസ്ഥ മൂന്നിന് രണ്ട് ഭാഗങ്ങളുണ്ട്. ഭാഗം ഒന്ന് ഹ്രസ്വകാലത്തേക്കും ഭാഗം രണ്ട് ദീർഘ കാലത്തേക്കും ആണ്.
ഭാഗം 1: വില ഹ്രസ്വകാലയളവിൽ ശരാശരി വിഭേദക ചെലവിനു തുല്യമോ അതിൽ കൂടുതലോ ആയിരിക്കണം (P ≥ AVC in the short run).
ശരാശരി വിഭേദക ചെലവിനേക്കാൾ താഴ്ന്ന വിലയ്ക്ക് സ്ഥാപനം ഉല്പന്നം ഉല്പാദിപ്പിക്കില്ല. ഡയഗ്രം 4.7 ൽ Q1 അളവ് ഉല്പന്നത്തിൽ വില P, AVC യേക്കാൾ താഴെയാണ്.
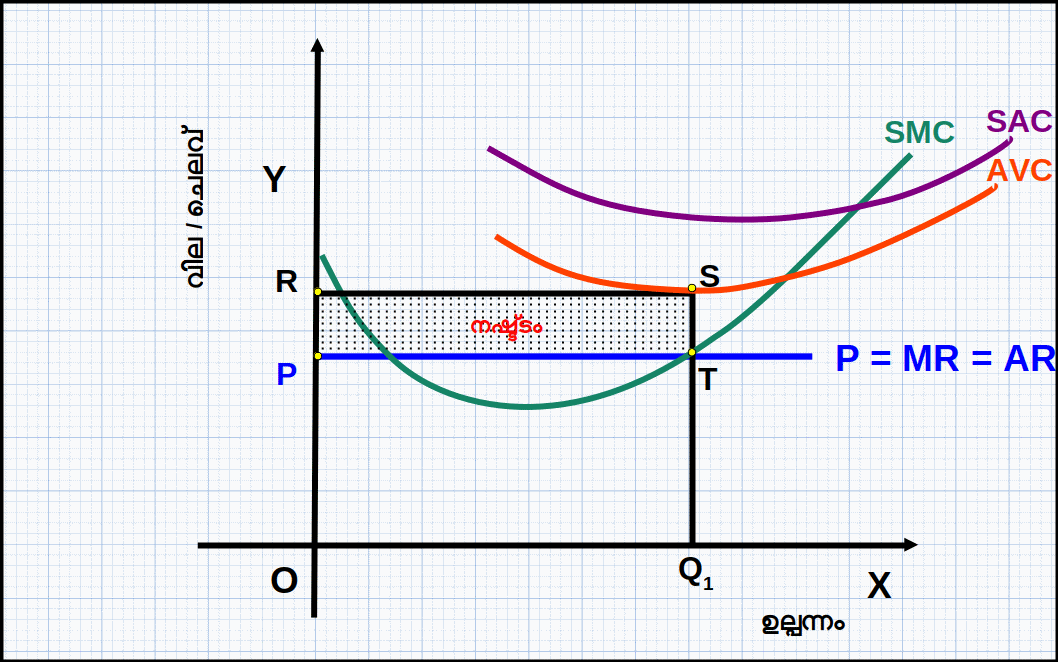
= OP × OQ1 = OPTQ1 എന്ന മേഖല. അതുപോലെ, Q1, ഉല്പന്ന തലത്തിലെ TVC: TVC = AVC × q
= OR × OQ1 = ORSQ1 എന്ന മേഖല. മൊത്തം ചെലവ് TFCയും TVCയും ചേർന്നതായതുകൊണ്ട് സ്ഥാപനത്തിന്റെ ലാഭം (Π): Π = TR – TC = TR – (TFC + TVC)
= TR – TFC – TVC
OPTQ1 – ORSQ1 – TFC ഇവിടെ വരുമാനത്തേക്കാൾ ചെലവ് കൂടുതലായതുകൊണ്ട് സ്ഥാപനത്തിന് നഷ്ടമായിരിക്കും. ഉല്പന്നം പൂജ്യമാണെങ്കിൽ സ്ഥാപനത്തിന്റെ TRഉം TVCയും പൂജ്യമാകുകയും ലാഭം (-) TFC ആയിരിക്കുകയും ചെയ്യും. അതായത് സ്ഥാപനത്തിന് TFC ക്ക് തുല്യമായ നഷ്ടം സംഭവിക്കുന്നു. അതു കൊണ്ട് സ്ഥാപനം വില AVC യെക്കാൾ കുറവാണെങ്കിൽ ഉല്പാദനം നടത്തുകയില്ല.
അപ്പോൾ, ലാഭം
л = TR – TC
= OPTQ1 – ORSQ1
= (-) PRST (ORSQ1 > OPTQ1)
ലാഭം പരമാവധിയാക്കൽ: ഗ്രാഫിക്കൽ അവതരണം (PROFIT MAXIMISATION PROBLEM: GRAPHICAL REPRESENTATION)
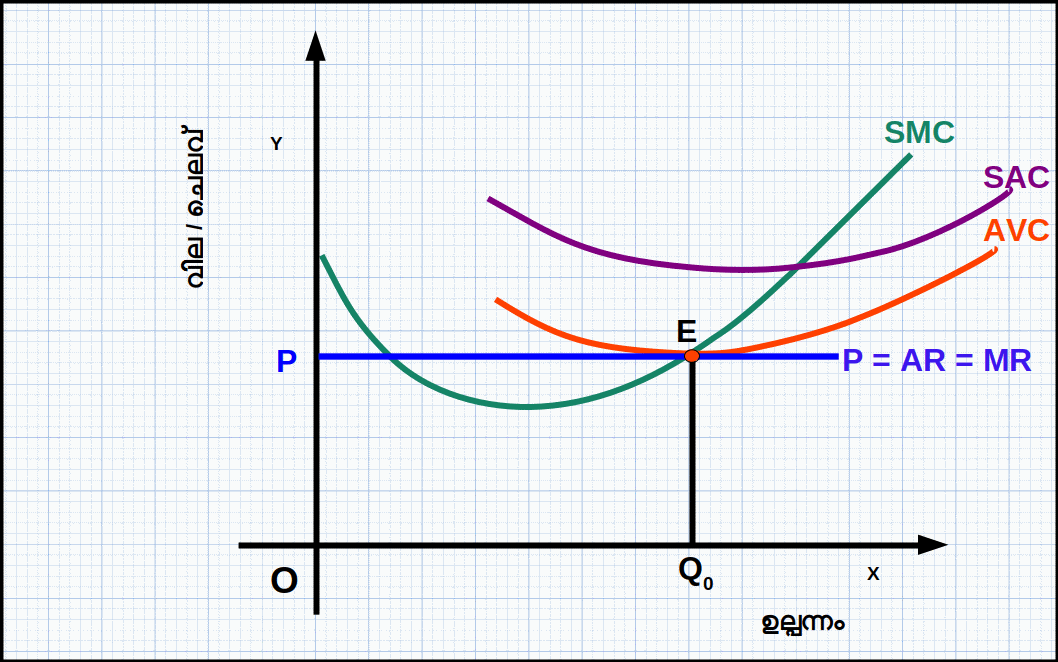
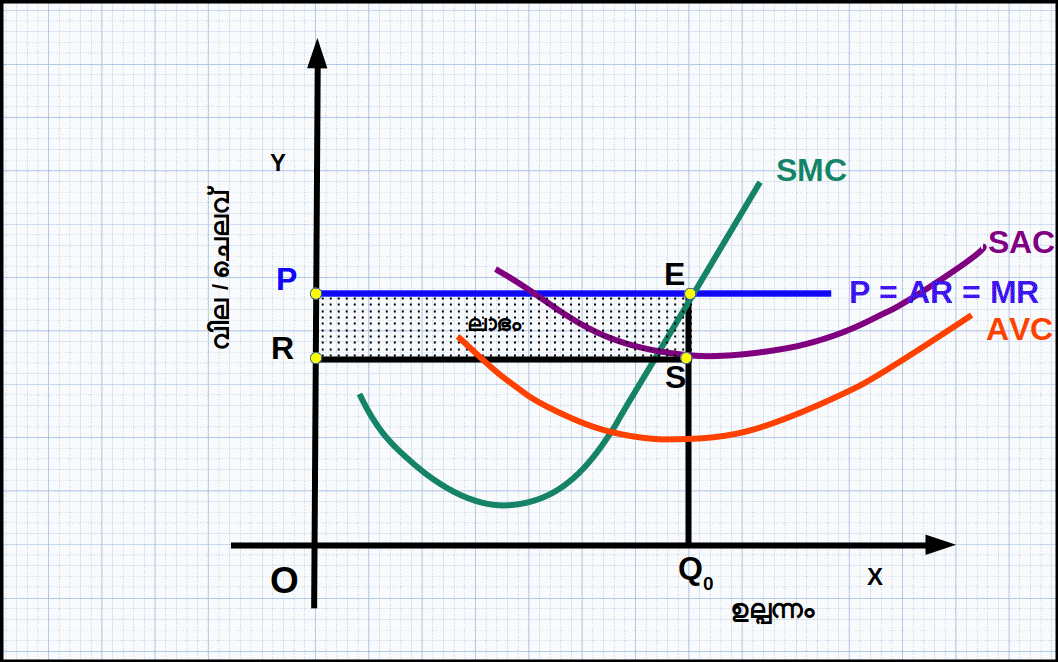
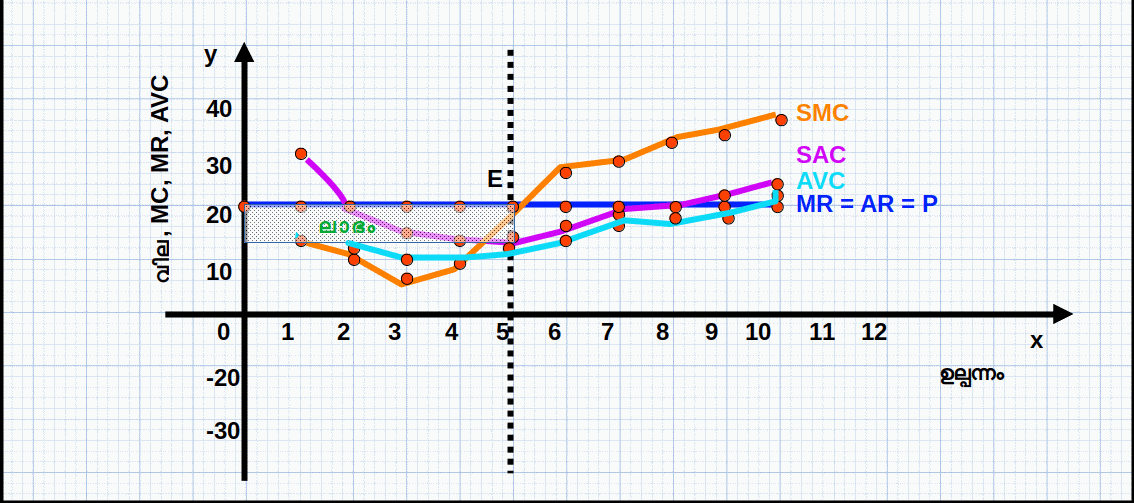
ഹ്രസ്വകാലയളവിൽ സമ്പൂർണ കിടമത്സര കമ്പോളത്തിലെ ഒരു സ്ഥാപനം ലാഭം പരമാവധിയാക്കുന്നത് ഒരു ഡയഗ്രത്തിന്റെ സഹായത്തോടെ വിവരിക്കാം. ഡയഗ്രം 4.11 ൽ Q0 എന്ന ഉല്പന്ന തലത്തിൽ സ്ഥാപനം സന്തുലിതാവസ്ഥയിലാണ്. E എന്ന ബിന്ദുവിൽ മൂന്ന് വ്യവസ്ഥകളും പാലിക്കപ്പെടുന്നു. അതായത്, Q0 ഉല്പന്ന തലത്തിൽ
- 1. P = MR = MC ആണ്.
- 2. SMC കുറഞ്ഞുകൊണ്ടിരിക്കുന്നില്ല
- 3. P ≥ AVC യാണ്
TR, TC വക്രങ്ങൾ ഉപയോഗിച്ച് ലാഭം പരമാവധിയാക്കുന്ന ജ്യാമിതീയ അവതരണം
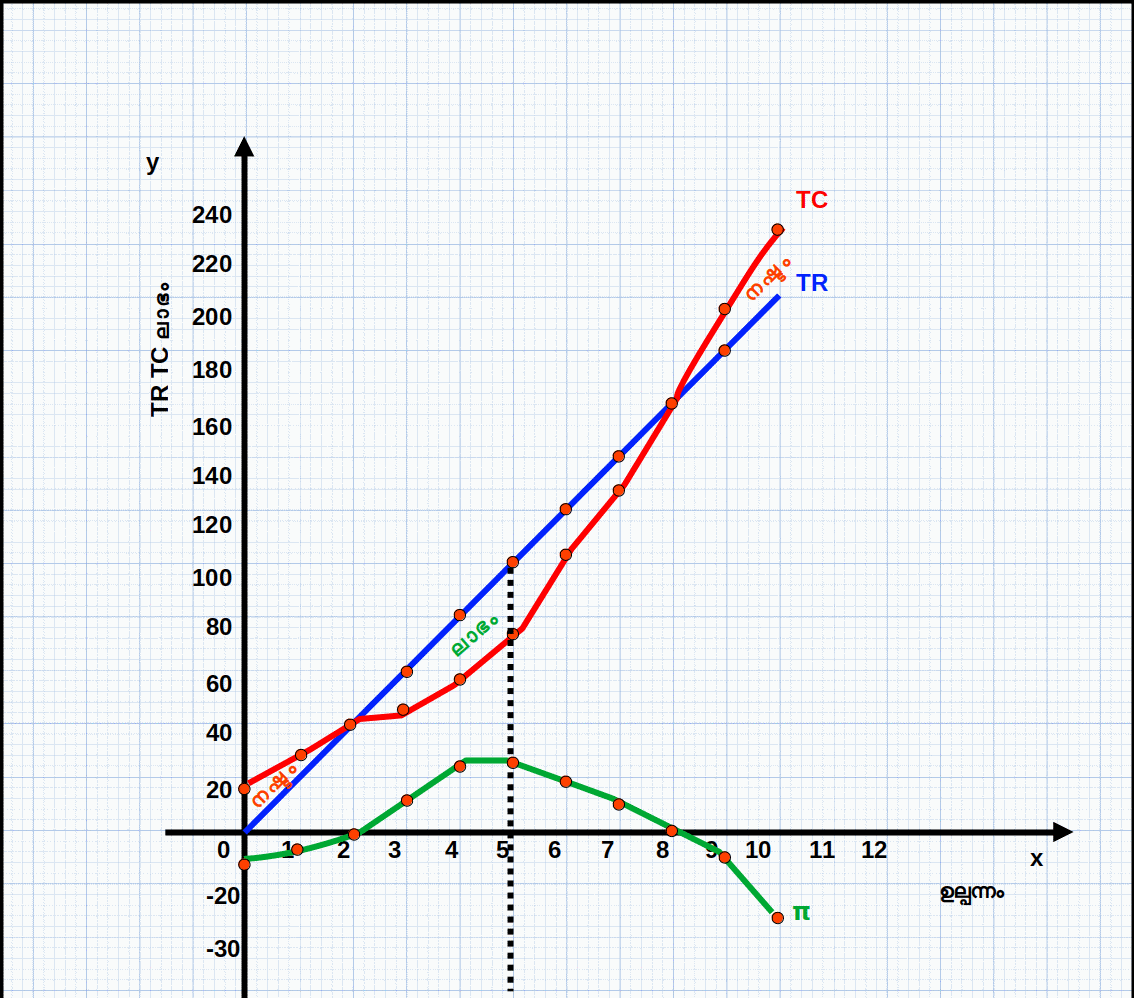
താഴെ കൊടുത്തിരിക്കുന്ന ഡയഗ്രത്തിന് മൂന്ന് ഭാഗങ്ങളുണ്ട്. ഒന്നാമത്തെ ഭാഗത്ത് TR, TC പ്രകങ്ങൾ കൊടുത്തിരിക്കുന്നു. രണ്ടാമത്തെ ഭാഗത്ത് MR, MC വക്രങ്ങൾ കൊടുത്തിരിക്കുന്നു. മൂന്നാമത്തെ ഭാഗത്ത് ലാഭ വക്രം കൊടുത്തിരിക്കുന്നു.
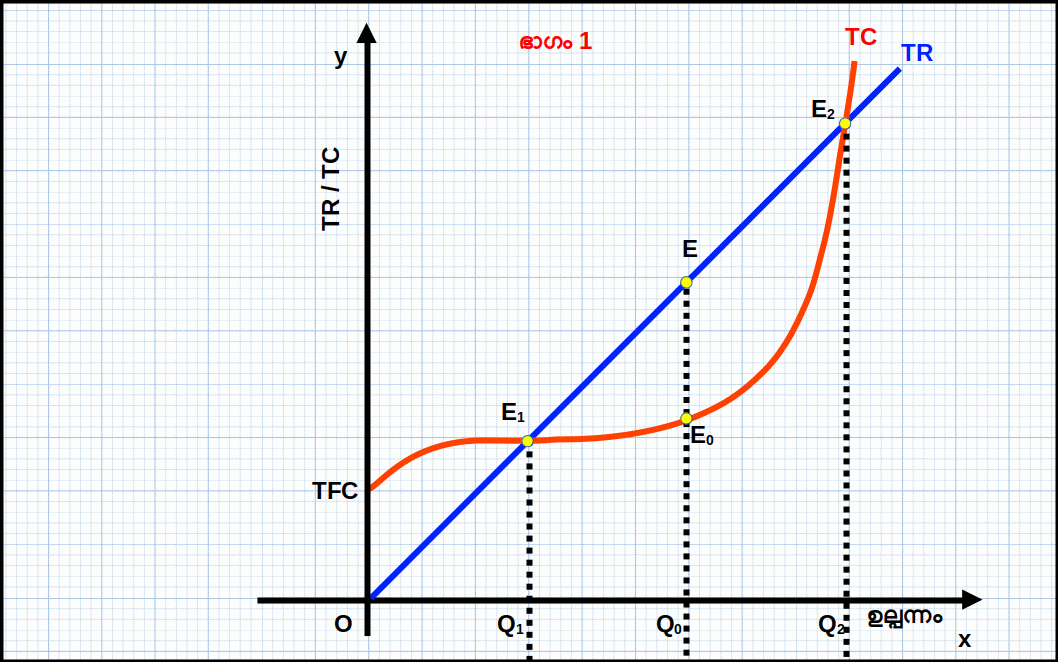
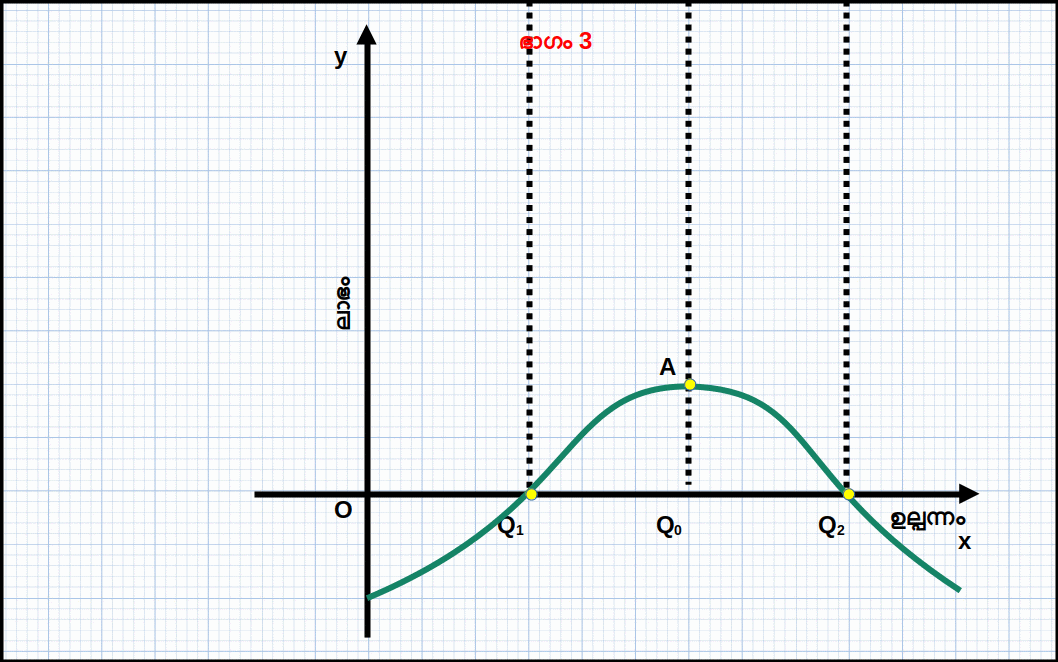
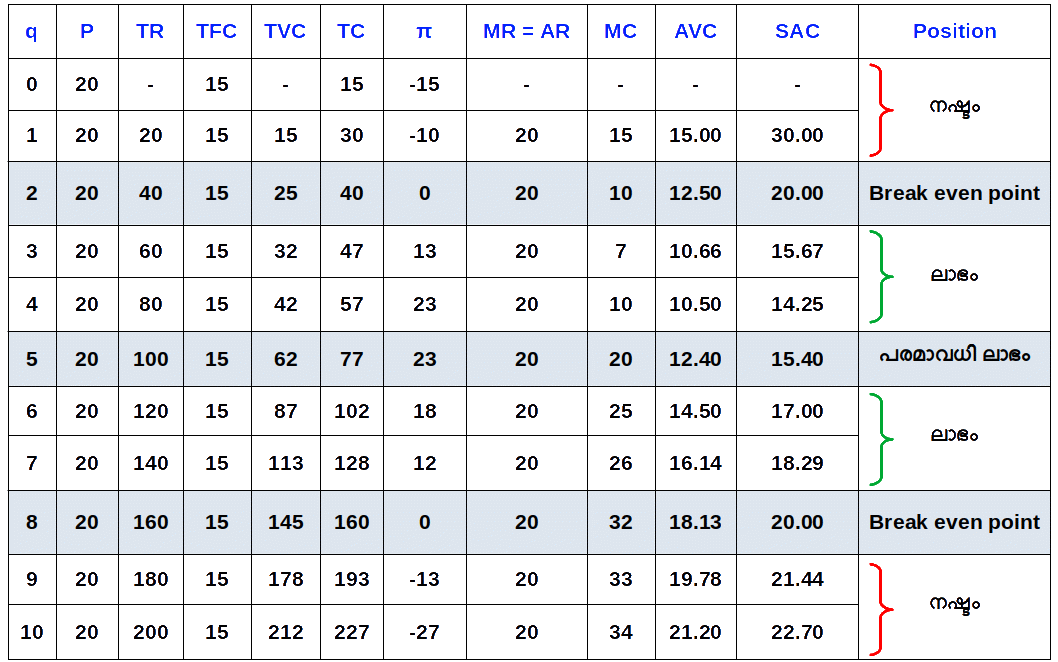
ഉല്പന്നത്തിന്റെ അളവ് 4 ലും 5 ലും എത്തുമ്പോൾ TR ഉം TC യും തമ്മിലുള്ള വ്യത്യാസം അഥവാ അകലം ഏറ്റവും കൂടിയിരിക്കുന്നു. അപ്പോൾ ലാഭം 23 യാണ്. ഇതാണ് ഏറ്റവും ഉയർന്ന ലാഭം. 5-ാമത്തെ ഉല്പന്ന യൂണിറ്റിലാണ് വിലയും (MR) MC യ്ക്ക് തുല്യമാകുന്നത് (P = MR = MC = 20). മാത്രമല്ല, 5-ാമത്തെ യൂണിറ്റിൽ MC കുറയുകയല്ല (വർധിക്കുകയാണ്). അതുപോലെ വില 20 എന്നത് AVC 12.40 എന്നതിനേക്കാൾ ഉയർന്നതാണ്. സമ്പൂർണ കിടമത്സര കമ്പോളത്തിന്റെ സന്തുലിതാവസ്ഥയുടെ മൂന്ന് വ്യവസ്ഥകളും പാലിക്കുന്നതുകൊണ്ട് സ്ഥാപനത്തിന് പരമാവധി ലാഭം ലഭിക്കുന്നത് 5-ാമത്തെ ഉല്പന്ന യൂണിറ്റിലാകുമ്പോഴാണ്. അതു കൊണ്ട് സന്തുലിത ഉല്പന്നം 5 ഉം സന്തുലിത വില 20 യുമാണ്.
അടച്ചുപൂട്ടൽ അവസ്ഥ (Shut down point)
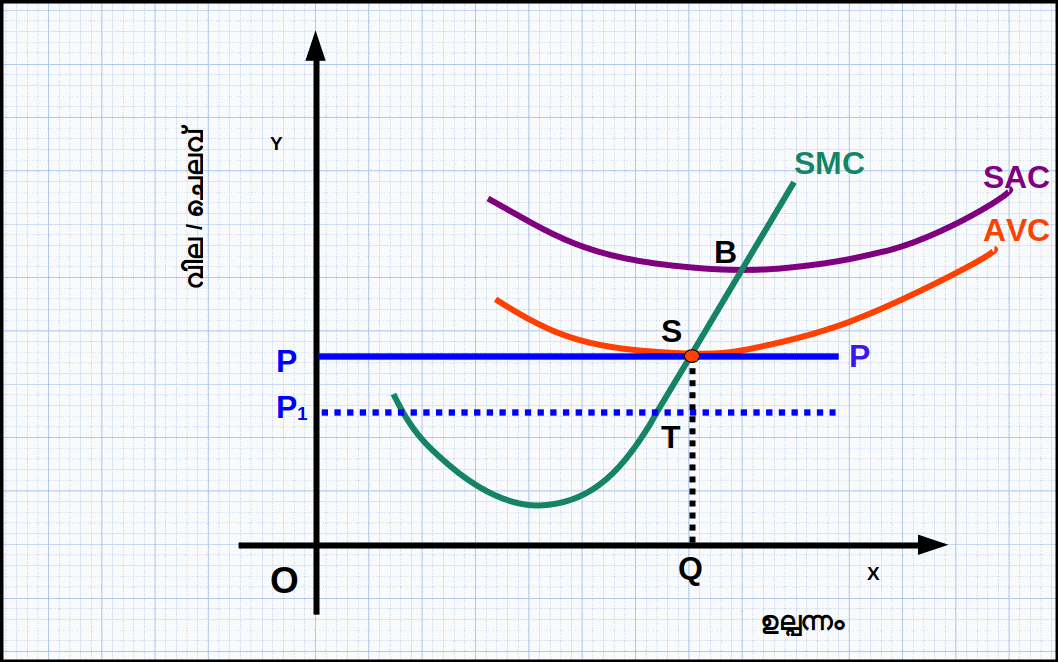
ഒരു ഉല്പാദക യൂണിറ്റ് ഉല്പാദനം നിർത്തിപ്പോകുന്ന സാഹചര്യത്തെയാണ് അടച്ചുപൂട്ടൽ അവസ്ഥ എന്നു പറയുന്നത്. സ്ഥാപനത്തിന് തുടർന്ന് ഉല്പാദനം നടത്തണമെങ്കിൽ ഉല്പന്നത്തിന് ഒരു മിനിമം വിലയെങ്കിലും ലഭിക്കണം. ഈ മിനിമം വില AVC നികത്താൻ കഴിയുന്ന വിലയായിരിക്കണം. AVC നികത്താൻ കഴിയുന്നില്ലെങ്കിൽ സ്ഥാപനം ഉല്പാദനം നിർത്തി അടച്ചുപൂട്ടൽ ഭീഷണിയിലാണ് എന്നർത്ഥം. അതായത് സ്ഥാപനം തുടർന്ന് പ്രവർത്തിക്കണമെങ്കിൽ AVC യുടെ മിനിമത്തിന് തുല്യമായ വില ലഭിക്കണം. അതുകൊണ്ട്, ശരാശരി വിഭേദകച്ചെലവിന്റെ മിനിമം ബിന്ദുവിനെ ഹ്രസ്വകാലയളവിലെ അടച്ചുപൂട്ടൽ ബിന്ദു എന്നു പറയുന്നു.
ഡയഗ്രം 4.14 ൽ S എന്ന ബിന്ദുവിൽ ഉല്പന്നത്തിന്റെ വില OP യും AVC യും (OP = QS) തുല്യമാണ്. ഈ വില AVC യുടെ മിനിമത്തിന് തുല്യമാണ്. OP വിലയ്ക്ക് സ്ഥാപനം OQ ഉല്പന്നം ഉല്പാദിപ്പിക്കുന്നു.
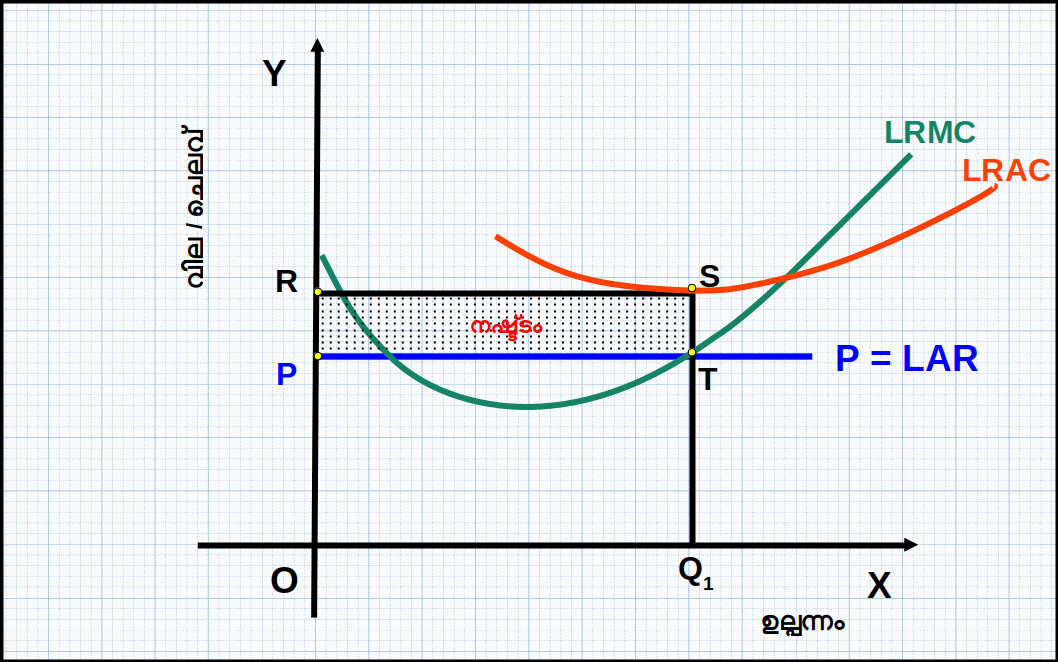
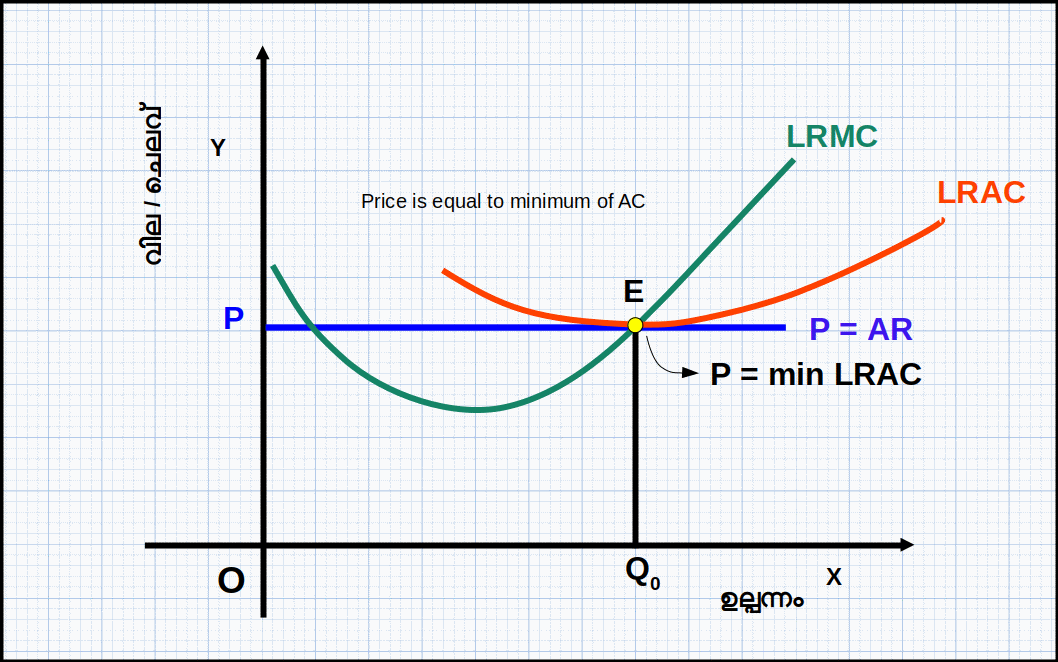
ദീർഘകാലയളവിലാണെങ്കിൽ ദീർഘകാല ശരാശരിച്ചെലവിന്റെ മിനിമമാണ് അടച്ചുപൂട്ടൽ ബിന്ദു (Minimum of LRAC). ദീർഘകാലാടിസ്ഥാനത്തിൽ ലാഭം പരമാവധിയാക്കാൻ ശ്രമിക്കുന്ന ഒരു സ്ഥാപനം LRACയെക്കാൾ കുറഞ്ഞ വില വരുന്ന സാഹചര്യത്തിൽ ഉല്പാദനം നിർത്തും. ഡയഗ്രം 4.15 ൽ S എന്ന ബിന്ദുവിൽ വിലയും LRAC യുടെ മിനിമവും തുല്യമാണ്. അപ്പോഴുള്ള വില OP യും ഉല്പന്നം OQ വുമാണ്. വില OPയ്ക് താഴെ വന്നാൽ സ്ഥാപനം ഉല്പാദനം നിർത്തി അടച്ചുപൂട്ടും. അതു കൊണ്ട് S എന്ന ബിന്ദുവാണ് ദീർഘകാലയളവിലെ അടച്ചുപൂട്ടൽ ബിന്ദു.
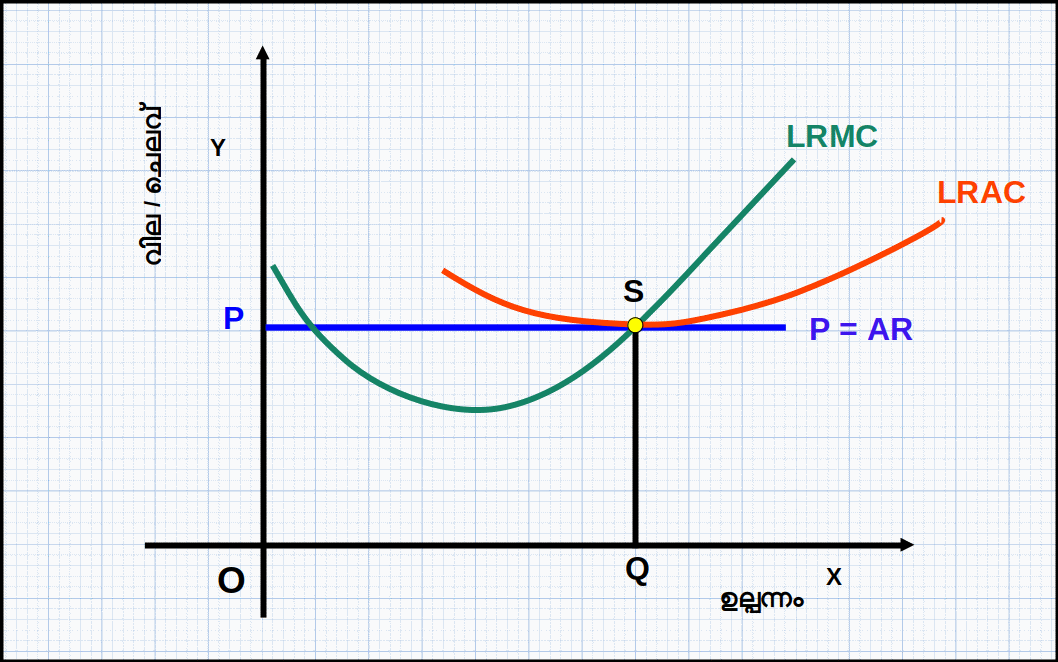

അടച്ചുപൂട്ടൽ ബിന്ദു
- P = minimum AVC (Short run).
- P = minimum LRAC (Long run).
സ്പഷ്ട ചെലവ് (Explicit Cost)
ഉല്പാദകൻ വിവിധ നിവേശങ്ങൾ അഥവാ ഉല്പാദന ഘടകങ്ങൾ മറ്റുള്ളവരിൽ നിന്നും വാടകയ്ക്കോ വിലയ്ക്കോ വാങ്ങുമ്പോൾ ഉല്പാദകനുണ്ടാകുന്ന പണച്ചെലവിനെയാണ് സ്പഷ്ട ചെലവ് എന്നു പറയുന്നത്. ഉദാഹരണമായി പാട്ടം, പലിശ, വേതനം, അസംസ്കൃതവസ്തുക്കൾക്കുള്ള ചെലവ് തുടങ്ങിയവ.
അവസരാത്മക ചെലവ് (Opportunity Cost)
ഉല്പാദക യൂണിറ്റിന് സ്വന്തമായി ചില ഉല്പാദന ഘടകങ്ങൾ ഉണ്ടാകാം. ഇവ സ്വന്തം സ്ഥാപനത്തിൽ ഉപയോഗിക്കുന്നതു മൂലം ആ ഉല്പാദക യൂണിറ്റിന് ചെലവ് വരുന്നില്ല. എന്നാൽ ഇവയുടെ സേവനം വേറെ ഏതെങ്കിലും ഉല്പാദക യൂണിറ്റിന് നല്കിയിരുന്നെങ്കിൽ അവയ്ക്ക് പ്രതിഫലം ലഭിക്കുമായിരുന്നു. ഇങ്ങനെ നഷ്ടപ്പെടുത്തി അഥവാ ഒഴിവാക്കിയ പ്രതിഫലത്തിൽ ഏറ്റവും നല്ലതിനെ അതിന്റെ അവസരാത്മക ചെലവ് (Opportunity cost) അഥവാ Trans- fer earning എന്നു പറയുന്നു. ഉദാഹരണം: സ്വന്തം സ്ഥാപനത്തിൽ മറ്റ് സാധാരണ തൊഴിലാളി കളെപ്പോലെ ജോലി ചെയ്യുന്ന ഉടമസ്ഥന് മറ്റ് ഏതെങ്കിലും സ്ഥാപനത്തിൽ ജോലി ചെയ്തിരുന്നാൽ കിട്ടുമായിരുന്ന വരുമാനത്തെ അവസരാത്മക ചെലവ് എന്നു പറയാം.
സാധാരണ ലാഭം (Normal Profit)
ഒരു ഉല്പാദക യൂണിറ്റിന് ഉല് പാദനം തുടർന്നു കൊണ്ടു പോകുന്നതിന് ആവശ്യമായ ഏറ്റവും കുറഞ്ഞ ലാഭത്തെ സാധാരണ ലാഭം എന്നു പറയുന്നു. അതായത്, ഒരു സ്ഥാപനത്തിന് ആ വ്യവസായത്തിൽ നിലനിൽക്കുന്നതിനാവശ്യമായ മിനിമം ലാഭമാണ് സാധാരണ ലാഭം. സാധാരണ ലാഭം ലഭിക്കുന്നില്ലെങ്കിൽ സ്ഥാപനത്തിന് ഉല്പാദനം തുടരാൻ സാധ്യമല്ല. ഹ്രസ്വകാലയളവിൽ സ്ഥാപനത്തിന് സാധാരണ ലാഭത്തെക്കാൾ കുറഞ്ഞ ലാഭമാണ് ലഭിക്കുന്നതെങ്കിലും ഉല്പാദനം തുടർന്നേക്കാം. എന്നാൽ ദീർഘ കാലയളവിൽ സ്ഥാപനത്തിന് സാധാരണ ലാഭത്തേക്കാൾ കുറവാണ് ലഭിക്കുന്നതെങ്കിൽ സ്ഥാപനം ഉല്പാദനം നിർത്തും. ദീർഘകാലയളവിൽ എല്ലാ സ്ഥാപനങ്ങൾക്കും സാധാരണ ലാഭമേ ലഭിക്കുകയുള്ളൂ.
സാധാരണ ലാഭം ഉല്പാദനച്ചെലവിന്റെ ഭാഗമാണ്. ഉല്പാദന ഘടകങ്ങളായ ഭൂമി, പ്രയത്നം, മൂല ധനം, സംഘാടനം എന്നിവയ്ക്കുള്ള പ്രതിഫലമായ പാട്ടം, വേതനം, പലിശ, ലാഭം എന്നിവ ചേർന്നതാണ് ഉല്പാദനച്ചെലവ്.
അതിസാധാരണ ലാഭം (Super Normal Profit)
ഒരു ഉല്പാദക യൂണിറ്റിന് സാധാരണ ലാഭത്തേക്കാൾ കൂടുതലായി ലഭിക്കുന്ന ലാഭത്തെ അതി സാധാരണ ലാഭം അഥവാ അമിതലാഭം (Abnormal Profit) എന്നു പറയുന്നു. ഇത് ഉല്പാദനച്ചെലവിന്റെ ഭാഗമല്ല. ഹ്രസ്വകാലയളവിൽ ചില സ്ഥാപനങ്ങൾക്ക് അമിതലാഭം ലഭിച്ചേക്കാം.ചില സ്ഥാപനങ്ങൾക്ക് നഷ്ടവുമാകാം. എന്നാൽ ദീർഘകാലയളവിൽ അമിതലാഭം ലഭിക്കുകയില്ല.
ലാഭ-നഷ്ട രഹിത ബിന്ദു (Break-even Point)
ഒരു ഉല്പാദക യൂണിറ്റിന്റെ മൊത്തം വരുമാനവും മൊത്തം ചെലവും തുല്യമാകുന്ന അവസ്ഥയെ ബ്രേക്ക് ഈവൻ പോയിന്റ് അഥവാ ലാഭ നഷ്ട രഹിത ബിന്ദു എന്നു പറയുന്നു. അതായത്, പൂജ്യ ലാഭം. സ്പഷ്ട ചെലവും അവസരാത്മക ചെലവും മൊത്തം ചെലവിന്റെ ഭാഗമാണെങ്കിൽ മൊത്തം വരുമാനവും മൊത്തം ചെലവും തുല്യമാകുന്ന ബിന്ദുവിൽ ഉല്പാദക യൂണിറ്റിന് സാധാരണ ലാഭം ഉണ്ടാകും. അതായത് ലാഭ-നഷ്ട രഹിത ബിന്ദുവിൽ ഉല്പാദക യൂണിറ്റിന് സാധാരണ ലാഭം മാത്രമേ ലഭിക്കുകയുള്ളൂ എന്നർത്ഥം.
Eg 4.6: പട്ടിക 4.4 ലും 4.13 ലും ഉല്പന്നം 2, 8 എന്നീ യൂണിറ്റുകളിൽ TC യും TR ഉം തുല്യമാണ്. 2-ാമത്തെ യൂണിറ്റിൽ TR = TC = 40 യും 8-ാമത്തെ യൂണിറ്റിൽ TR = TC = 160 ഉം ആണ്. ഈ അവസ്ഥയെയാണ് ലാഭ-നഷ്ട രഹിത ബിന്ദു എന്നു പറയുന്നത്.
ഹ്രസ്വകാലയളവിൽ SAC വക്രത്തിന്റെ മിനിമം ബിന്ദുവും ദീർഘകാലയളവിൽ LRAC വക്രത്തിന്റെ മിനിമം ബിന്ദുവുമാണ് ബ്രേക്ക് ഈവൻ പോയിന്റ് അഥവാ ലാഭ-നഷ്ട രഹിത ബിന്ദു. ഡയഗ്രം 4.14 ൽ B എന്ന ബിന്ദുവും ഡയഗ്രം 4.15 ൽ S എന്ന ബിന്ദുവും.
പ്രദാനം (Supply) ഒരു ഉല്പാദക യൂണിറ്റ് ഒരു നിശ്ചിത വിലയ്ക്ക് ഒരു നിശ്ചിത സമയത്ത് കമ്പോളത്തിൽ വില്ക്കാൻ തയ്യാറായ ഉല്പന്നത്തിന്റെ അളവിനെ പ്രദാനം എന്നു പറയുന്നു. അതായത്, കമ്പോളത്തിൽ വില്ക്കാൻ വച്ചിരിക്കുന്ന സാധനത്തിന്റെ അളവാണ് പ്രദാനം.
ഒരു സ്ഥാപനത്തിന്റെ പ്രദാന വക്രം(Supply Curve of a firm)
ഒരു ഉല്പാദക യൂണിറ്റ് ഒരു നിശ്ചിത സമയത്ത് വ്യത്യസ്ത വിലകൾക്ക് കമ്പോളത്തിൽ വില്ക്കാൻ തയ്യാറാവുന്ന സാധനത്തിന്റെ വിവിധ അളവുകളെ സൂചിപ്പിക്കുന്ന ഗ്രാഫിനെ പ്രദാന വക്രം എന്നു പറയുന്നു. പ്രദാന വക്രത്തെ ഹ്രസ്വകാല പ്രദാന വക്രം ദീർഘകാല പ്രദാന വക്രം എന്നിങനെ തിരിച്ചിരിക്കുന്നു.
ഒരു സ്ഥാപനത്തിന്റെ ഹ്രസ്വകാല പ്രദാന വക്രം (Short-run supply curve of a firm)
ശരാശരി വിഭേദക ചെലവ് വക്രത്തിന്റെ മിനിമത്തിൽ നിന്നു തുടങ്ങി ഹ്രസ്വകാല സീമാന്ത ചെലവ് വക്രത്തിന്റെ ഉയർന്നുപോകുന്ന ഭാഗമാണ് ഒരു ഉല്പാദക യൂണിറ്റിന്റെ ഹ്രസ്വകാല പ്രദാന വക്രം. അതായത്, AVC വക്രത്തിന്റെ മിനിമം മുതലുള്ള SMC വക്രത്തിന്റെ ഉയർന്നുപോകുന്ന
ഭാഗം.
ലാഭം പരമാവധിയാക്കാൻ ശ്രമിക്കുന്ന ഒരു സ്ഥാപനത്തിന്റെ SMC വക്രത്തിൽനിന്ന് ഹ്രസ്വകാല പ്രദാന വക്രം രൂപീകരിക്കുന്നതെങ്ങനെയെന്ന് നമുക്ക് നോക്കാം. ഹ്രസ്വകാല പ്രദാന വക്രത്തിന്റെ രൂപീകരണം രണ്ട് സാഹചര്യങ്ങളിലൂടെ വിശദമാക്കാം. ഒന്നാമതായി വില AVC യുടെ മിനിമത്തിന് തുല്യമോ അതിൽ കൂടുതലോ ആകുമ്പോഴുള്ള സന്തുലിത ഉല്പന്നം/പ്രദാനം എത്രയാണെന്ന് നിർണയിക്കുന്നു. രണ്ടാമതായി വില AVC യുടെ മിനിമത്തിന് താഴെയാകുമ്പോൾ സന്തുലിത ഉല്പന്നം പ്രദാനം എത്രയാണെന്ന് നിർണയിക്കുന്നു.
സാഹചര്യം 1: വില AVC യുടെ മിനിമമോ അതിൽ കൂടുതലോ ആയാൽ
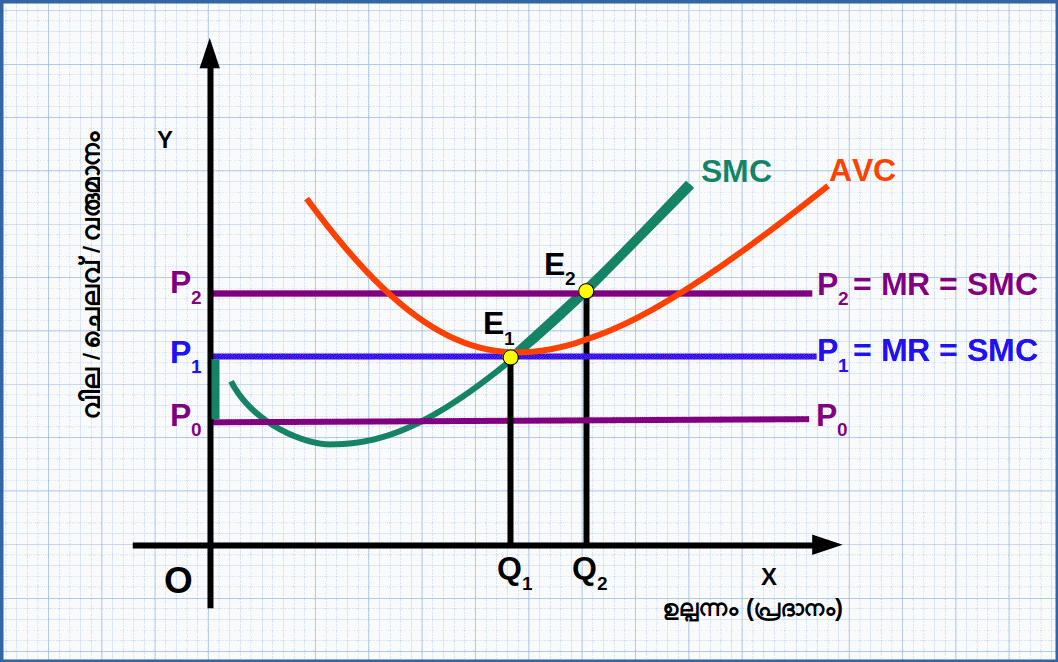
സാഹചര്യം 2: വില AVC യുടെ മിനിമത്തേക്കാൾ കുറഞ്ഞാൽ (P < minimum of AVC).
വില AVC യുടെ മിനിമത്തേക്കാൾ താഴെയാണെങ്കിൽ പ്രദാനം പൂജ്യമായിരിക്കും. ഡയഗ്രം 4.16 ൽ വില P0 ആണെങ്കിൽ സ്ഥാപനം ഉല്പന്നം ഉല്പാദിപ്പിക്കുവാൻ തയ്യാറാവില്ല. P0 വില അടച്ചുപൂട്ടൽ ബിന്ദുവിന് താഴെയാണ്. ഈ സാഹചര്യത്തിൽ സന്തുലിതാവസ്ഥയുടെ മൂന്നാമത്തെ വ്യവസ്ഥ പാലിക്കുന്നില്ല. അതുകൊണ്ട് AVC യുടെ മിനിമത്തിന് താഴെയുള്ള ഏതു വിലയിലും പ്രദാനം പൂജ്യമായിരിക്കും. ഹ്രസ്വകാല പ്രദാന വക്ര രൂപീകരണത്ത നമുക്ക് ഇങ്ങനെ സംഗ്രഹിക്കാം. വില AVC യുടെ മിനിമത്തേക്കാൾ കുറവാണെങ്കിൽ പ്രദാനം പൂജ്യവും, AVC യുടെ മിനിമമാണെങ്കിൽ പ്രദാനം പോസിറ്റീവും, AVC യുടെ മിനിമത്തേക്കാൾ കൂടുകയാണെങ്കിൽ പ്രദാനം വർധിക്കുകയും ചെയ്യുന്നു. AVC യുടെ മിനിമത്തിന് താഴെയുള്ള എല്ലാ വിലകളിലും ഉല്പന്നം പൂജ്യമായിരിക്കും. AVC യുടെ മിനിമത്തിൽനിന്ന് തുടങ്ങി SMC വക്രത്തിന്റെ മുകളിലേക്ക് ഉയർന്നുപോകുന്ന ഭാഗമാണ് ഒരു ഉല്പാദക യൂണിറ്റിന്റെ ഹ്രസ്വകാല പ്രദാന വക്രം എന്ന് നിർവചിക്കാം.ഡയഗ്രം 4.16 ൽ SMC വക്രത്തിന്റെ തടിച്ച ഭാഗമാണ് ഹ്രസ്വകാല പ്രദാന വക്രം.ഒരു സ്ഥാപനത്തിന്റെ ദീർഘകാല പ്രദാന വക്രം (Long run supply curve of a firm)
ദീർഘകാല ശരാശരി ചെലവ് (LRAC) വക്രത്തിന്റെ മിനിമത്തിൽ നിന്ന് തുടങ്ങി ദീർഘ കാല സീമാന്ത ചെലവ് (LRMC) വക്രത്തിന്റെ ഉയർന്നുപോകുന്ന ഭാഗമാണ് ഒരു സ്ഥാപനത്തിന്റെ ദീർഘകാല പ്രദാന വക്രം.
ഹ്രസ്വകാല പ്രദാന വക്രം രൂപീകരിച്ചതു പോലെ ദീർഘകാല പ്രദാന വക്രം -LRMC വക്രത്തിൽനിന്ന് രൂപീകരിക്കാം. ആദ്യം വില LRAC യുടെ മിനിമത്തിന് തുല്യമോ അതിൽ കൂടുതലോ ആകുമ്പോഴുള്ള സന്തുലിത ഉല്പന്നം പ്രദാനം എത്രയെന്ന് നിർണയിക്കുന്നു. അതിനുശേഷം വില LRAC യുടെ മിനിമത്തിന് താഴെയാകുമ്പോൾ സന്തുലിത ഉല്പന്നം എത്രയെന്ന് നിർണയിക്കുന്നു.
സാഹചര്യം 1: വില LRAC യുടെ മിനിമമോ അതിൽ കൂടുതലോ ആയാൽ (P ≥ minimum of LRAC).
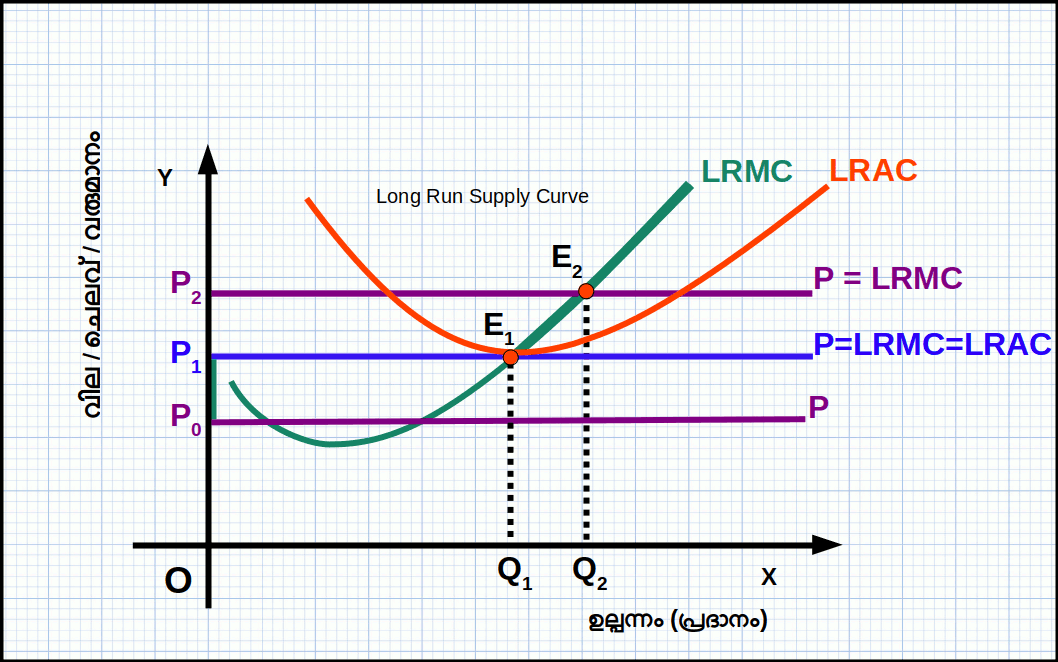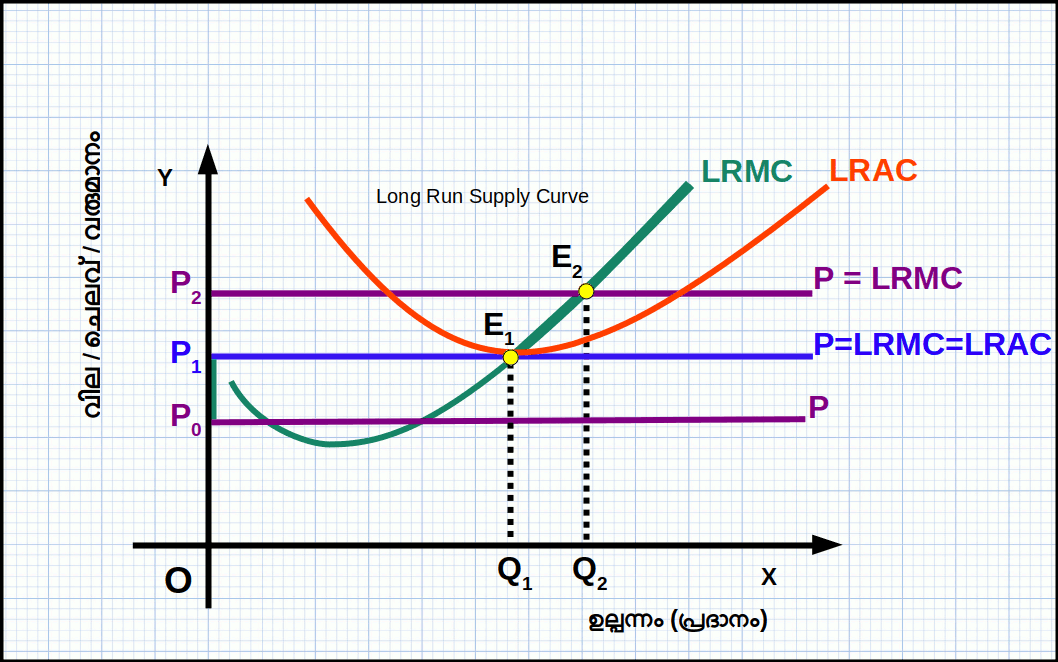
വില LRAC യുടെ മിനിമത്തേക്കാൾ കൂടുതലാണെങ്കിൽ ഉല്പന്നത്തിന്റെ അളവ് വർധിക്കുന്നു. ഡയഗ്രത്തിൽ വില P1 ൽ നിന്ന് ആയി വർധിച്ചപ്പോൾ വില രേഖയും SMC വക്രവും സന്ധിക്കുന്ന (ഖണ്ഡിക്കുന്ന) E2 എന്ന സന്തുലിത ബിന്ദുവിൽ ലാഭം പരമാവധിയാകുന്ന ഉല്പന്നത്തിന്റെ അളവ് q1 ൽ നിന്ന് q1 ആയി വർധിക്കുന്നു. വില വർധിച്ചപ്പോൾ സന്തുലിത പ്രദാനവും വർധിക്കുന്നു.
സാഹചര്യം 2: വില LRAC യുടെ മിനിമത്തേക്കാൾ കുറഞ്ഞാൽ (P < minimum of LRAC).
വില LRAC യുടെ മിനിമത്തേക്കാൾ താഴെയാണെങ്കിൽ ഉല്പന്നം പൂജ്യമായിരിക്കും. ഡയഗ്രം 4.18 ൽ വില P0 ആണെങ്കിൽ സ്ഥാപനം ഉല്പന്നം ഉല്പാദിപ്പിക്കുവാൻ തയ്യാറല്ല. P0 വില അടച്ചുപൂട്ടൽ ബിന്ദുവിന് (E1) താഴെയാണ്. ഈ സാഹചര്യത്തിൽ സന്തുലിതാവസ്ഥയുടെ മൂന്നാമത്തെ വ്യവസ്ഥ പാലിക്കുന്നില്ല. അതുകൊണ്ട് LRAC യുടെ മിനിമത്തിന് താഴെയുള്ള ഏതു വിലയിലും പ്രദാനം പൂജ്യമായിരിക്കും. ദീർഘകാല പ്രദാന വക്ര രൂപീകരണത്തെ നമുക്ക് ഇങ്ങനെ സംഗ്രഹിക്കാം. വില LRAC യുടെ മിനിമത്തെക്കാൾ കുറവാണെങ്കിൽ പ്രദാനം പൂജ്യവും, LRAC യുടെ മിനിമമാണെങ്കിൽ പ്രദാനം പോസിറ്റീവും, LRAC യുടെ മിനിമത്തെക്കാൾ കൂടുതലാണെങ്കിൽ പ്രദാനം വർധിക്കുകയും ചെയ്യുന്നു. അതുകൊണ്ട് LRAC യുടെ മിനിമത്തിന് താഴെയുള്ള എല്ലാ വിലകളിലും ഉല്പന്നം പൂജ്യവും, LRAC യുടെ മിനിമത്തിൽനിന്ന് തുടങ്ങി LRMC വക്രത്തിന്റെ മുകളിലേക്ക് ഉയർന്നു പോകുന്ന ഭാഗമാണ് ഒരു സ്ഥാപനത്തിന്റെ ദീർഘകാല പ്രദാന വക്രം എന്ന് നിർവചിക്കാം. ഡയഗ്രം 4.18 ൽ LRMC വക്രത്തിന്റെ തടിച്ച ഭാഗമാണ് ദീർഘകാല പ്രദാന വക്രം.ഒരു ഉല്പാദക യൂണിറ്റിന്റെ പ്രദാന വക്രത്തിന്റെ നിർണ്ണായകങ്ങൾ. (Determinants of a Firm’s Supply Curve)
ഒരു ഉല്പാദക യൂണിറ്റിന്റെ പ്രദാന വക്രം അതിന്റെ MC വക്രത്തിന്റെ ഭാഗമാണെന്ന് നാം കണ്ടു. അതുകൊണ്ട് MC വക്രത്തെ ബാധിക്കുന്ന ഏതു ഘടകവും തീർച്ചയായും പ്രദാന വക്രത്തിന്റെ നിർണായകങ്ങൾ അഥവാ നിർണയിക്കുന്ന ഘടകങ്ങളാണ്. അത്തരത്തിൽ പ്രദാന വക്രത്തെ ബാധിക്കുന്ന പ്രധാനപ്പെട്ട മൂന്ന് ഘടകങ്ങളാണ് സാങ്കേതിക പുരോഗതി, നിവേശവിലകൾ, യൂണിറ്റ് ടാക്സ്. ഇവ പ്രദാന വക്രത്തെ എങ്ങനെ സ്വാധീനിക്കുന്നുവെന്ന് ചർച്ച ചെയ്യാം.
1. സാങ്കേതിക പുരോഗതി (Technical progress)
സീമാന്ത ചെലവിനെ അഥവാ പ്രദാന വക്രത്തെ നിർണയിക്കുന്ന ഒരു പ്രധാന ഘടകമാണ് സാങ്കേതിക പുരോഗതി. നല്ല സാങ്കേതിക വിദ്യ ഉപയോഗിക്കുമ്പോൾ MC കുറയുകയും മോശം സാങ്കേതിക വിദ്യ ഉപയോഗിച്ചാൽ MC വർധിക്കുകയും ചെയ്യും.സാങ്കേതിക പുരോഗതി (Technical Progress)
ഒരു നിശ്ചിത അളവ് നിവേശങ്ങൾകൊണ്ട് കൂടുതൽ അളവ് ഉല്പന്നം ഉല്പാദിപ്പിക്കാൻ കഴിയുന്ന അവസ്ഥ അല്ലെങ്കിൽ നിശ്ചിത അളവ് ഉല്പന്നം കുറഞ്ഞ അളവ് നിവേശങ്ങൾകൊണ്ട് ഉല്പാദിപ്പിക്കാൻ കഴിയുന്ന അവസ്ഥ സാങ്കേതിക പുരോഗതിയായി കണക്കാക്കാം.
2. നിവേശ വിലകൾ (Input prices)
ഒരു സ്ഥാപനത്തിന്റെ പ്രദാന വക്രത്തെ സ്വാധീനിക്കുന്ന പ്രധാനപ്പെട്ട മറ്റൊരു ഘടകമാണ് നിവേശങ്ങളുടെ വിലകൾ. നിവേശങ്ങളുടെ വില കുറഞ്ഞാൽ MC കുറയുകയും തന്മൂലം പ്രദാന വക്രം വലത്തേക്ക് താഴേക്ക് മാറുകയും ചെയ്യും. അതു പോലെ, നിവേശങ്ങളുടെ വിലകൾ വർധിച്ചാൽ MC വർധിക്കുന്നതുമൂലം പ്രദാന വക്രം ഇടത്തേക്ക് മുകളിലേക്ക് മാറുന്നു.3. യൂണിറ്റ് ടാക്സ് (Unit tax)
ഉല്പന്നത്തിന്റെ ഓരോ യൂണിറ്റ് ഉല്പാദിപ്പിച്ച് വിൽക്കുമ്പോൾ ഗവൺമെന്റ് ചുമത്തുന്ന നികുതിയാണ് യൂണിറ്റ് ടാക്സ്. ഉദാഹരണമായി, ഒരു സ്ഥാപനം 10 യൂണിറ്റ് സാധനം ഉല്പാദിപ്പിക്കുന്നു. ഒരു യൂണിറ്റിന് 2 യൂണിറ്റ് ടാക്സ് ഗവൺമെന്റ് ചുമത്തിയപ്പോൾ മൊത്തം നികുതി 10 × 2 = 20.യൂണിറ്റ് ടാക്സ് വർധിപ്പിച്ചാൽ MC വർധിക്കുന്നതുമൂലം പ്രദാന വക്രം ഇടത്തേക്ക് മുകളിലേക്ക് മാറുന്നു. അതുപോലെ യൂണിറ്റ് ടാക്സ് കുറച്ചാൽ MC കുറയുന്നതുമൂലം പ്രദാന വക്രം വലത്തേക്ക് താഴേക്ക് മാറുന്നു. ഇത് ഡയഗ്രം 4.19 ന്റെ സഹായത്തോടെ വിശദമാക്കാം.
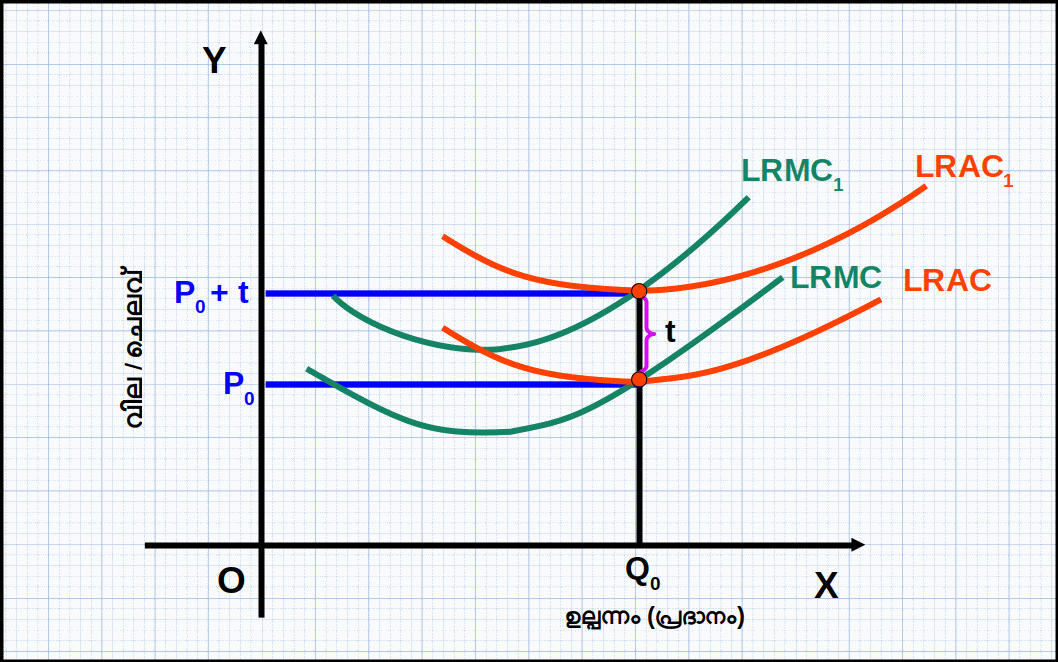
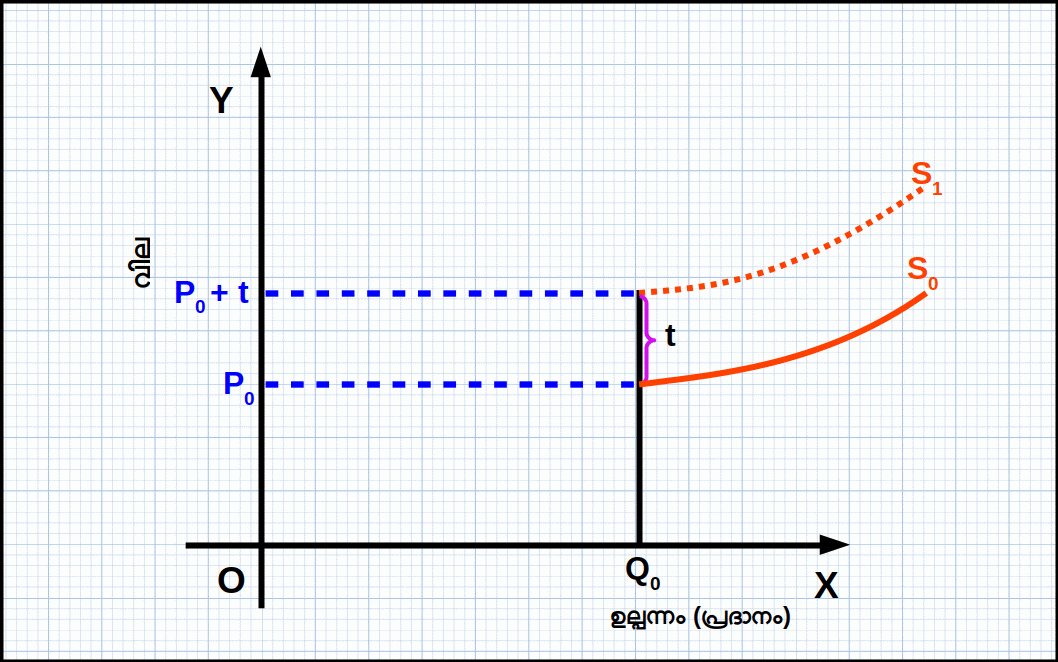
ദീർഘകാല പ്രദാന വക്രം LRAC വക്രത്തിന്റെ മിനിമത്തിൽനിന്ന് തുടങ്ങി LRMC വക്രത്തിന്റെ ഉയർന്നു പോകുന്ന ഭാഗമായതുകൊണ്ട് ഡയഗ്രം 4.20 ൽ S0, S1, എന്നിവയാണ് യഥാക്രമം യൂണിറ്റ് ടാക്സ് ചുമത്തുന്നതിനു മുമ്പും അതിനു ശേഷവുമുള്ള പ്രദാന വക്രങ്ങൾ. അതായത്, S0 എന്ന പ്രദാന വക്രം യൂണിറ്റ് ടാക്സ് ചുമത്തിയതുമൂലം S1 ആയി ഇടത്തേക്ക് മാറിയിരിക്കുന്നു.
പ്രദാന ധർമം (Supply Function)
സാങ്കേതിക വിദ്യ, നിവേശങ്ങളുടെ വില, യൂണിറ്റ് ടാക്സ് എന്നിവ പ്രദാനത്തെ എങ്ങനെ സ്വാധീനിക്കുന്നുവെന്ന് നമ്മൾ കണ്ടു. ഇവ കൂടാതെ മറ്റ് അനേകം ഘടകങ്ങൾ പ്രദാനത്തെ സ്വാധീനിക്കുന്നുണ്ട്. സാധനത്തിന്റെ വില, മറ്റു സാധനങ്ങളുടെ വില, ഉല്പാദന യൂണിറ്റിന്റെ ലക്ഷ്യം, കാലാവസ്ഥ, ആഗോള രാഷ്ട്രീയ സാമ്പത്തിക പ്രശ്നങ്ങൾ അങ്ങനെ പോകുന്നു അവ. പ്രദാനത്തെ ബാധിക്കുന്ന ഈ ഘടകങ്ങളിൽ മാറ്റമുണ്ടാകുമ്പോൾ സാധനത്തിന്റെ പ്രദാനത്തിലുള്ള അളവിലും മാറ്റമുണ്ടാകുന്നു. അതുപോലെ പ്രദാനത്തിലുള്ള മാറ്റം ഘടകങ്ങളിലും മാറ്റമുണ്ടാക്കുന്നു. ആയതിനാൽ, ഒരു സാധനത്തിന്റെ പ്രദാനവും അതിനെ ബാധിക്കുന്ന ഘടകങ്ങളും തമ്മിലുള്ള ബന്ധത്തെ പ്രദാന ധർമം എന്നു പറയുന്നു.
പ്രദാന നിയമം (Law of Supply)
ഒരു സാധനത്തിന്റെ പ്രദാനത്തെ ബാധിക്കുന്ന ഏറ്റവും പ്രധാനപ്പെട്ട ഘടകം ആ സാധനത്തിന്റെ വിലയാണ്. വിലയും പ്രദാനവും തമ്മിലുള്ള ബന്ധം പ്രദാന നിയമം വ്യക്തമാക്കുന്നു. വിലയിലുള്ള മാറ്റം പ്രദാനത്തെയും പ്രദാനത്തിലുള്ള മാറ്റം വിലയെയും സ്വാധീനിക്കുന്നു. പ്രദാനം S ഉം വില P യും ആയാൽ പ്രദാനം വിലയെ ആശ്രയിച്ചിരിക്കുന്നു എന്ന അർത്ഥത്തിൽ, പ്രദാനം വിലയുടെ ധർമ്മമായി. പ്രദാന ധർമത്തെ ബീജഗണിത രൂപത്തിൽ,
S = f (P) എന്ന രൂപത്തിൽ പ്രസ്ഥാപിക്കാം. ഇവിടെ പ്രദാനത്തെ നിർണയിക്കുന്ന മറ്റ് ഘടകങ്ങൾ പരിഗണിക്കുന്നില്ല. എന്താണ് വിലയും പ്രദാനവും തമ്മിലുള്ള ബന്ധം?
MC വക്രത്തിന്റെ ഭാഗമായ പ്രദാന വക്രം വിലയും പ്രദാനവും തമ്മിലുള്ള പോസിറ്റീവ് ബന്ധത്തെ സൂചിപ്പിക്കുന്നു. അതായത്, മറ്റ് ഘടകങ്ങളിൽ മാറ്റമില്ലായെങ്കിൽ വില വർധിക്കുമ്പോൾ പ്രദാനം വർധിക്കുകയും വില കുറയുമ്പോൾ പ്രദാനം കുറയുകയും ചെയ്യുന്നു. ഇതിനെ പ്രദാന നിയമം എന്നു പറയുന്നു. മറ്റൊരു വിധത്തിൽ പറഞ്ഞാൽ, വിലയും പ്രദാനവും തമ്മിലുള്ള പോസിറ്റീവ് ബന്ധത്തെ പ്രദാന നിയമം എന്നു പറയുന്നു.
പ്രദാന ധർമ സമവാക്യം പ്രദാന ധർമ സമവാക്യം വിലയും പ്രദാനവും തമ്മിലുള്ള ബന്ധത്തെ വ്യക്തമാക്കുന്നു. പ്രദാനത്തിന്റെ അളവ്, S ഉം വില, P യും ആയാൽ പ്രദാന നിയമത്തെ അഥവാ പ്രദാന ധർമ്മത്തെ ബീജഗണിത രൂപത്തിൽ താഴെ കൊടുത്തിരിക്കുന്നതുപോലെ നിർവചിക്കാം.
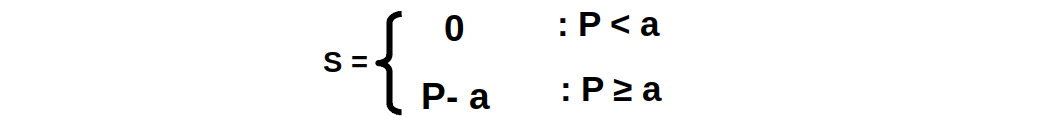 ഈ പ്രദാന ധർമ സമവാക്യത്തിൽ a ഒരു സ്ഥിര മൂല്യമാണ്. നെഗറ്റീവ് പ്രദാനത്തിന് സാമ്പത്തിക ശാസ്ത്രത്തിൽ അർത്ഥമില്ലാത്തതുകൊണ്ട് വില a യേക്കാൾ കുറവായാൽ പ്രദാനം പൂജ്യമായിരിക്കും. വില a യ് തുല്യമോ അതിൽ കൂടുതലോ ആയാൽ പ്രദാന ധർമം S = P – a ആയിരിക്കും.
ഈ പ്രദാന ധർമ സമവാക്യത്തിൽ a ഒരു സ്ഥിര മൂല്യമാണ്. നെഗറ്റീവ് പ്രദാനത്തിന് സാമ്പത്തിക ശാസ്ത്രത്തിൽ അർത്ഥമില്ലാത്തതുകൊണ്ട് വില a യേക്കാൾ കുറവായാൽ പ്രദാനം പൂജ്യമായിരിക്കും. വില a യ് തുല്യമോ അതിൽ കൂടുതലോ ആയാൽ പ്രദാന ധർമം S = P – a ആയിരിക്കും.പ്രദാനവകം ശരാശരി ചെലവു വകത്തിന്റെ മിനിമം മുതൽ മുകളിലേക്കുള്ള സീമാന്ത ചെലവു വകത്തിന്റെ ഉയർന്നുപോകുന്ന ഭാഗമായതുകൊണ്ട് a യുടെ മൂല്യം ശരാശരി ചെലവ് വകത്തിന്റെ മിനിമം പോയിന്റിന് തൊട്ട് താഴെയുള്ള വിലയായിരിക്കും. ആയതിനാൽ S … എന്ന സമവാക്യം വിലയും പ്രദാനവും തമ്മിലുള്ള പോസിറ്റീവ് ബന്ധത്തെ പ്രസ്ഥാപിക്കുന്നു. Eg 4.8; ഒരു ഉല്പാദക യൂണിറ്റിന്റെ പ്രദാന ധർമ സമവാക്യം താഴെ കൊടുക്കുന്നു.
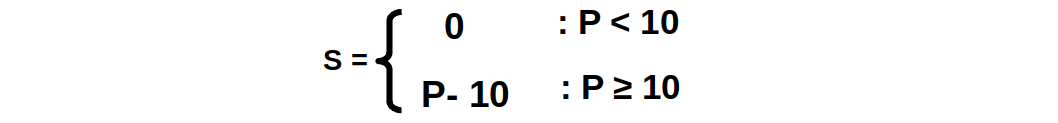 ഈ പ്രദാന ധർമ സമവാക്യത്തിന്റെ ആദ്യ ഭാഗം സൂചിപ്പിക്കുന്നത് വില 10ൽ താഴെയായാൽ പ്രദാനം പൂജ്യമായിരിക്കും എന്നാണ്. ഉദാഹരണമായി വില 9 ആയാൽ, S = 9 – 10 = − 1 ആണ്. പ്രദാനം നെഗറ്റീവായ തുകൊണ്ട് പൂജ്യമായി പരിഗണിക്കുന്നു.
ഈ പ്രദാന ധർമ സമവാക്യത്തിന്റെ ആദ്യ ഭാഗം സൂചിപ്പിക്കുന്നത് വില 10ൽ താഴെയായാൽ പ്രദാനം പൂജ്യമായിരിക്കും എന്നാണ്. ഉദാഹരണമായി വില 9 ആയാൽ, S = 9 – 10 = − 1 ആണ്. പ്രദാനം നെഗറ്റീവായ തുകൊണ്ട് പൂജ്യമായി പരിഗണിക്കുന്നു.ഈ സമവാക്യത്തിന്റെ രണ്ടാമത്തെ ഭാഗം സൂചിപ്പിക്കുന്നത് വില 10 യോ അതിൽ കൂടുതലോ ആയാൽ പ്രദാനം S = P – 10 ആയിരിക്കും എന്നാണ്. വില 10 മുതൽ 15 വരെയായാൽ പ്രദാനം എത്രയാണെന്ന് നമുക്ക് നോക്കാം.
വ്യക്തിഗത പ്രദാന പട്ടിക (Individual Supply Schedule)
ഒരു ഉല്പാദകൻ ഒരു കമ്പോളത്തിൽ വിവിധ വിലകളിൽ വില്പനയ്ക്ക് തയ്യാറായ ഒരു സാധനത്തിന്റെയോ സേവനത്തിന്റെയോ വിവിധ അളവുകൾ കാണിക്കുന്ന പട്ടികയാണ് വ്യക്തിഗത പ്രദാന പട്ടിക. അതായത് ഒരു ഉല്പാദക യൂണിറ്റ് വിവിധ വിലയ്ക്ക് പ്രദാനം ചെയ്യാൻ തയ്യാറുള്ള ഉല്പന്നത്തിന്റെ അളവുകൾ.
Eg 4.9: മുൻ ഉദാഹരണത്തിൽ കൊടുത്ത സമവാക്യം ഉപയോഗിച്ച് കണ്ടെത്തിയ പ്രദാനത്തിന്റെ വിവിധ അളവുകളും അവയുടെ വിലകളും താഴെ പട്ടിക 4.6 ൽ കൊടുത്തിരിക്കുന്നത് ഒരു വ്യക്തിഗത പ്രദാന പട്ടികയാണ്.
| Table 4.6 വ്യക്തിഗത പ്രദാന പട്ടിക | ||
|---|---|---|
| വില | പ്രദാനത്തിന്റെ അളവുകൾ | |
| 9 | 0 | |
| 10 | 0 | |
| 11 | 1 | |
| 12 | 2 | |
| 13 | 3 | |
| 14 | 4 | |
| 15 | 5 | |
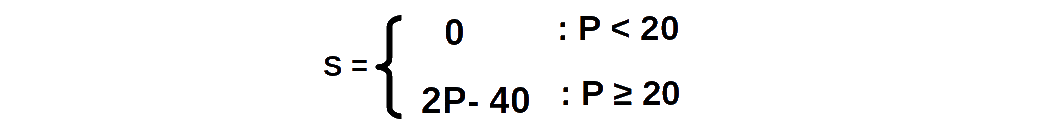 വില 20 മുതൽ 25 വരെ കാണിക്കുന്ന ഒരു വ്യക്തിഗത പ്രദാന പട്ടിക നിർമിക്കുക.
വില 20 മുതൽ 25 വരെ കാണിക്കുന്ന ഒരു വ്യക്തിഗത പ്രദാന പട്ടിക നിർമിക്കുക.Solution
P = 20, S(P) = 2 x 20 – 40 = 40 – 40 = 0 P = 21, S(P) = 2 x 21 – 40 = 42 – 40 = 2 P = 22, S(P) = 2 x 22 – 40 = 44 – 40 = 4 P = 23, S(P) = 2 x 23 – 40 = 46 – 40 = 6 P = 24, S(P) = 2 x 24 – 40 = 48 – 40 = 8 P = 25, S(P) = 2 x 25 – 40 = 50 – 40 = 10 വ്യക്തിഗത പ്രദാന പട്ടിക താഴെ കൊടുക്കുന്നു.
| Table 4.7 Individual Supply Schedule | ||
|---|---|---|
| വില (P) | പ്രദാനം (S = 2P- 40) | |
| 20 | 2 × 20 – 40 = 40 – 40 = 0 | |
| 21 | 2 × 21 – 40 = 42 – 40 = 2 | |
| 22 | 2 × 22 – 40 = 44 – 40 = 4 | |
| 23 | 2 × 23 – 40 = 46 – 40 = 6 | |
| 24 | 2 × 24 – 40 = 48 – 40 = 8 | |
| 25 | 2 × 25 – 40 = 50 – 40 = 10 | |
വ്യക്തിഗത പ്രദാന വക്രം (Individual Supply Curve)
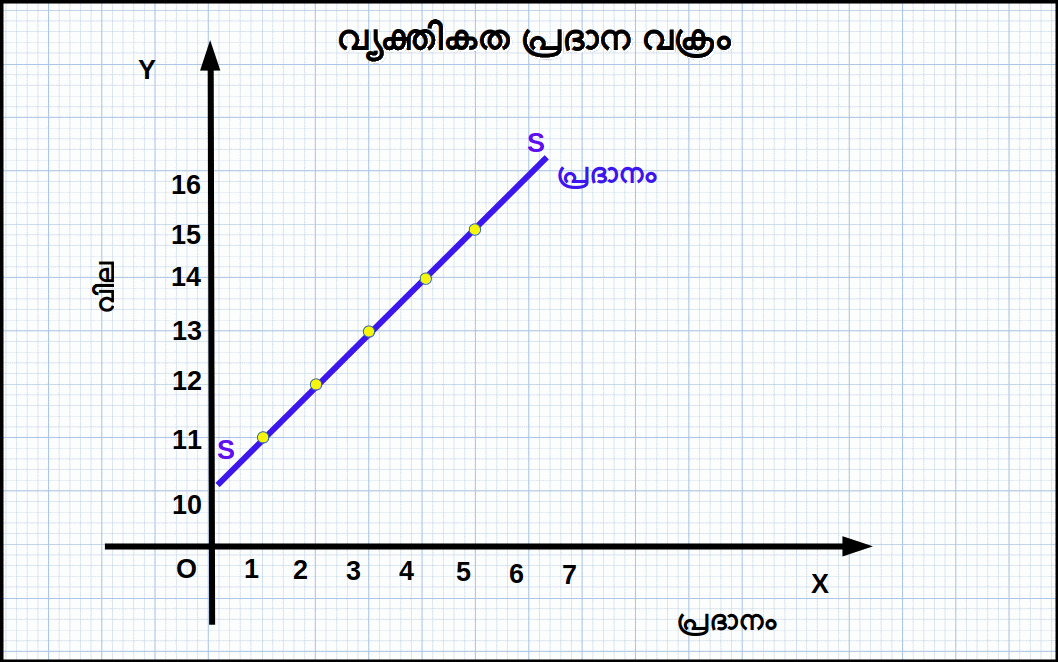
വ്യക്തിഗത പ്രദാന പട്ടികയുടെ ഗ്രാഫിക്കൽ ആവിഷ്കാരമാണ് വ്യക്തിഗത പ്രദാന വക്രം. ഒരു ഉല്പാദക യൂണിറ്റിന്റെ ഒരു ഉല്പന്നത്തിന്റെ പ്രദാനവും അതിന്റെ വിലയും തമ്മിലുള്ള ബന്ധം കാണിക്കുന്ന രേഖാ ചിത്രമാണ് വ്യക്തിഗത പ്രദാന വക്രം.
Eg 4.10: പട്ടിക 4.6 ൽ കൊടുത്ത വ്യക്തിഗത പ്രദാന പട്ടികയുടെ വ്യക്തിഗത പ്രദാന വക്ര ഗ്രാഫ് 4.20 ൽ കൊടുത്തിരിക്കുന്നു.
കമ്പോള പ്രദാനം (Market Supply)
ഒരു കമ്പോളത്തിലെ എല്ലാ ഉല്പാദകരും കൂടി ഒരു നിശ്ചിത വിലയ്ക്ക് പ്രദാനം ചെയ്യുന്ന ഒരു സാധനത്തിന്റെ മൊത്തം അളവിനെ കമ്പോള പ്രദാനം എന്നു പറയുന്നു. ഒരു നിശ്ചിത വിലയ്ക്ക് ഒരു കമ്പോളത്തിലുള്ള ഒരേ സാധനം ഉല്പാദിപ്പിക്കുന്ന എല്ലാ ഉല്പാദക യൂണിറ്റിന്റേയും പ്രദാനത്തിന്റെ ആകെ തുകയാണ് ഇത്.
Eg 4.11: ഒരു കമ്പോളത്തിൽ A, B, C എന്നിങ്ങനെ മൂന്ന് നെല്ലുല്പാദകരുണ്ട്. 15 രൂപയ്ക്ക് A 100 Kg യും B 50 Kg യും C 200 Kg യും നെല്ല് പ്രദാനം ചെയ്യുന്നു. അപ്പോൾ 15 രൂപയ്ക്ക് കമ്പോള പ്രദാനം, Sm = 100 + 50 + 200 = 350 Kg ആണ്.
കമ്പോള പ്രദാന പട്ടിക (Market Supply Schedule) വ്യക്തിഗത പ്രദാന പട്ടികകളുടെ തിരശ്ചീനമായി കൂട്ടിയ തുകയാണ് കമ്പോള പ്രദാന പട്ടിക.
വിവിധ വിലയ്ക്ക് ഒരു കമ്പോളത്തിൽ ഒരേ ഉല്പന്നം പ്രദാനം ചെയ്യുന്ന എല്ലാ ഉല്പാദകരുടെയും പ്രദാനത്തിന്റെ അളവുകൾ സമാന്തരമായി കൂട്ടിയാൽ കമ്പോള പ്രദാന പട്ടിക ലഭിക്കും. Eg 4.12; ഒരു കമ്പോളത്തിൽ A, B, എന്നീ മൂന്ന് ഉല്പാദകരുടെ വ്യക്തിഗത പ്രദാന പട്ടികയിൽനിന്ന് കമ്പോള പ്രദാന പട്ടിക നിർമിച്ചിരിക്കുന്ന വിധം താഴെ കൊടുത്തിരിക്കുന്നു.| Table 4.8 വ്യക്തിഗത പ്രദാന പട്ടികയും കമ്പോള പ്രദാന പട്ടികയും | |||||
|---|---|---|---|---|---|
| ഉല്പാദകൻ A | ഉല്പാദകൻ B | കമ്പോള പ്രദാന പട്ടിക (A യുടെ പ്രദാനം + B യുടെ പ്രദാനം) |
|||
| വില | പ്രദാനം | വില | പ്രദാനം | വില | പ്രദാനം |
| 10 | 0 | 10 | 0 | 10 | 0 |
| 15 | 2 | 15 | 0 | 15 | 2 |
| 20 | 4 | 20 | 1 | 20 | 5 |
| 25 | 6 | 25 | 2 | 25 | 8 |
| 30 | 8 | 30 | 3 | 30 | 11 |
വില 10 രൂപയായിരുന്നപ്പോൾ കമ്പോള പ്രദാനം പൂജ്യമാണ് (0 + 0 = 0). വില 15 രൂപയായിരുന്നപ്പോൾ കമ്പോള പ്രദാനം 2 (= 2 + 0 = 2) ആണ്. വില 20 രൂപയായിരുന്നപ്പോൾ കമ്പോള പ്രദാനം 5 (= 4 + 1 = 5) ആണ്. ഇത് അങ്ങനെ പോകുന്നു.
Eg 4.13: പ്രദാന ധർമ സമവാക്യം ഉപയോഗിച്ച് കമ്പോള പ്രദാന പട്ടിക നിർമിക്കുന്നതെങ്ങനെയെന്ന് നോക്കാം. ഒരു കമ്പോളത്തിൽ രണ്ട് ഉല്പാദകർ ഉണ്ടെന്ന് കരുതുക. അവരുടെ വ്യക്തിഗത പ്രദാന സമവാക്യങ്ങൾ താഴെ കൊടുക്കുന്നു.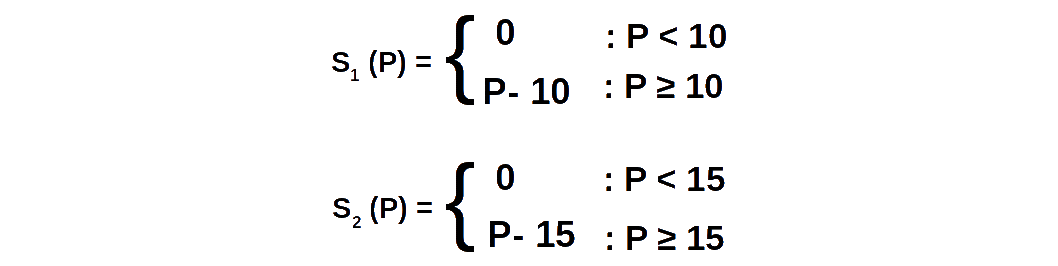 S1(P) ഒന്നാമത്തെ ഉല്പാദകന്റെ പ്രദാന ധർമവും S2(P) രണ്ടാമത്തെ ഉല്പാദകന്റെ പ്രദാന ധർമവുമാണ്. കമ്പോള പ്രദാന ധർമ [Sm (P)] സമവാക്യം കാണാൻ ഈ രണ്ട് വ്യക്തിഗത പ്രദാന സമവാക്യങ്ങൾ തമ്മിൽ കൂട്ടിയാൽ മതി. അതായത്,
S1(P) ഒന്നാമത്തെ ഉല്പാദകന്റെ പ്രദാന ധർമവും S2(P) രണ്ടാമത്തെ ഉല്പാദകന്റെ പ്രദാന ധർമവുമാണ്. കമ്പോള പ്രദാന ധർമ [Sm (P)] സമവാക്യം കാണാൻ ഈ രണ്ട് വ്യക്തിഗത പ്രദാന സമവാക്യങ്ങൾ തമ്മിൽ കൂട്ടിയാൽ മതി. അതായത്,= P – 10 + P – 15
= 2P – 25
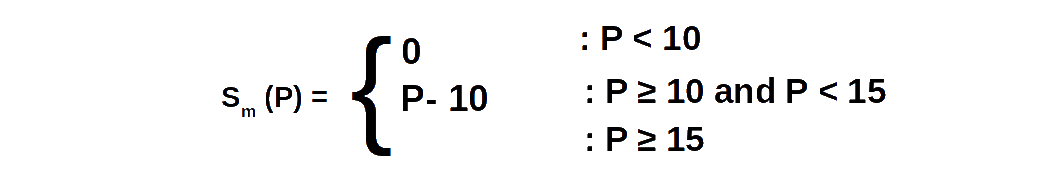 എന്ന് കമ്പോള പ്രദാന ധർമത്തെ പ്രസ്ഥാപിക്കാം. ഈ സമവാക്യത്തിൽ വില 10 ൽ താഴെയാണെങ്കിൽ കമ്പോള പ്രദാനം പൂജ്യമായിരിക്കും. വില പത്തോ അതിന് മുകളിൽ 15 ന് താഴെ വരെയാണെങ്കിൽ കമ്പോള പ്രദാനം Sm (P) = P – 10 ആയിരിക്കും. വില പതിനഞ്ചോ അതിൽ കൂടുതലോ ആണെങ്കിൽ കമ്പോള പ്രദാനം Sm (P) = 2P – 25 ആയിരിക്കും.
എന്ന് കമ്പോള പ്രദാന ധർമത്തെ പ്രസ്ഥാപിക്കാം. ഈ സമവാക്യത്തിൽ വില 10 ൽ താഴെയാണെങ്കിൽ കമ്പോള പ്രദാനം പൂജ്യമായിരിക്കും. വില പത്തോ അതിന് മുകളിൽ 15 ന് താഴെ വരെയാണെങ്കിൽ കമ്പോള പ്രദാനം Sm (P) = P – 10 ആയിരിക്കും. വില പതിനഞ്ചോ അതിൽ കൂടുതലോ ആണെങ്കിൽ കമ്പോള പ്രദാനം Sm (P) = 2P – 25 ആയിരിക്കും.ഉദാഹരണമായി, വില 10 മുതൽ 20 വരെ ആയാൽ വ്യക്തിഗത പ്രദാന പട്ടികയും കമ്പോള പ്രദാന പട്ടികയും താഴെ കൊടുക്കുന്നു.
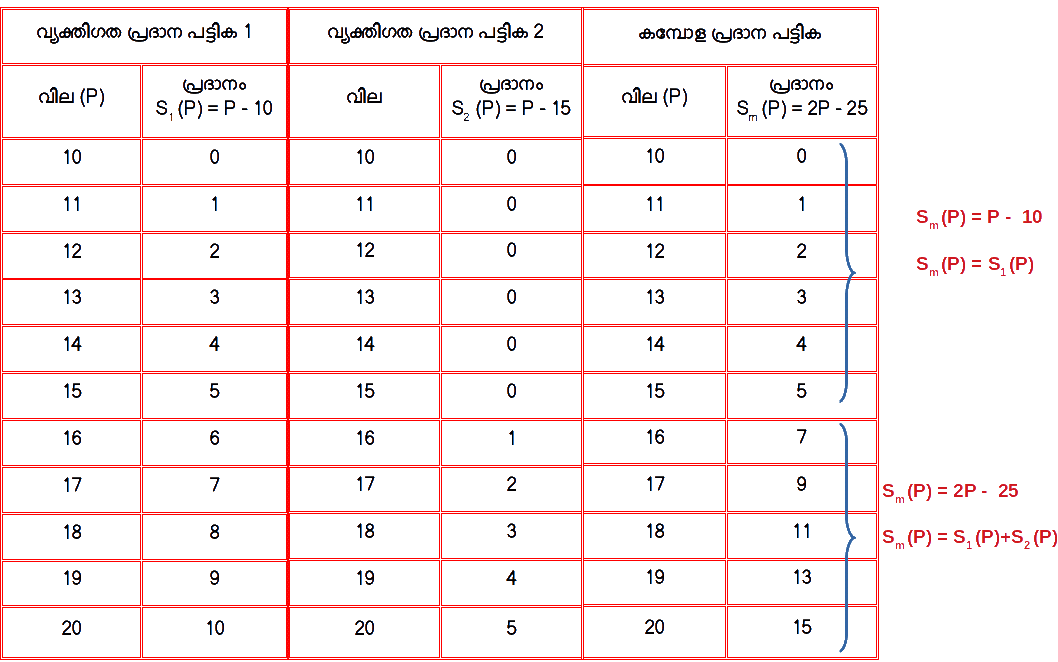 കമ്പോള പ്രദാന പട്ടികയിൽ വില 10 മുതൽ 14 വരെ കമ്പോള പ്രദാനം ഒന്നാമത്തെ വ്യക്തിഗത പ്രദാന പട്ടിക തന്നെയാണ്. എന്തുകൊണ്ടെന്നാൽ, അതുവരെ S2(p) = 0 ആണ്. വില 15 മുതൽ മുകളിലേക്ക് കമ്പോള പ്രദാനം (പട്ടിക) ഒന്നാമത്തെയും രണ്ടാമത്തെയും വ്യക്തിഗത പ്രദാന പട്ടികകളുടെ തുകയാണ്.
കമ്പോള പ്രദാന പട്ടികയിൽ വില 10 മുതൽ 14 വരെ കമ്പോള പ്രദാനം ഒന്നാമത്തെ വ്യക്തിഗത പ്രദാന പട്ടിക തന്നെയാണ്. എന്തുകൊണ്ടെന്നാൽ, അതുവരെ S2(p) = 0 ആണ്. വില 15 മുതൽ മുകളിലേക്ക് കമ്പോള പ്രദാനം (പട്ടിക) ഒന്നാമത്തെയും രണ്ടാമത്തെയും വ്യക്തിഗത പ്രദാന പട്ടികകളുടെ തുകയാണ്.
കമ്പോള പ്രദാന വക്രം (Market Supply Curve)
കമ്പോള പ്രദാന പട്ടികയുടെ ഗ്രാഫിനെ കമ്പോള പ്രദാന വക്രം എന്നു പറയുന്നു. വ്യക്തിഗത പ്രദാന വക്രങ്ങൾ തിരശ്ചീനമായി കൂട്ടിയാണ് കമ്പോള പ്രദാന വക്രം നിർമിക്കുന്നത്.
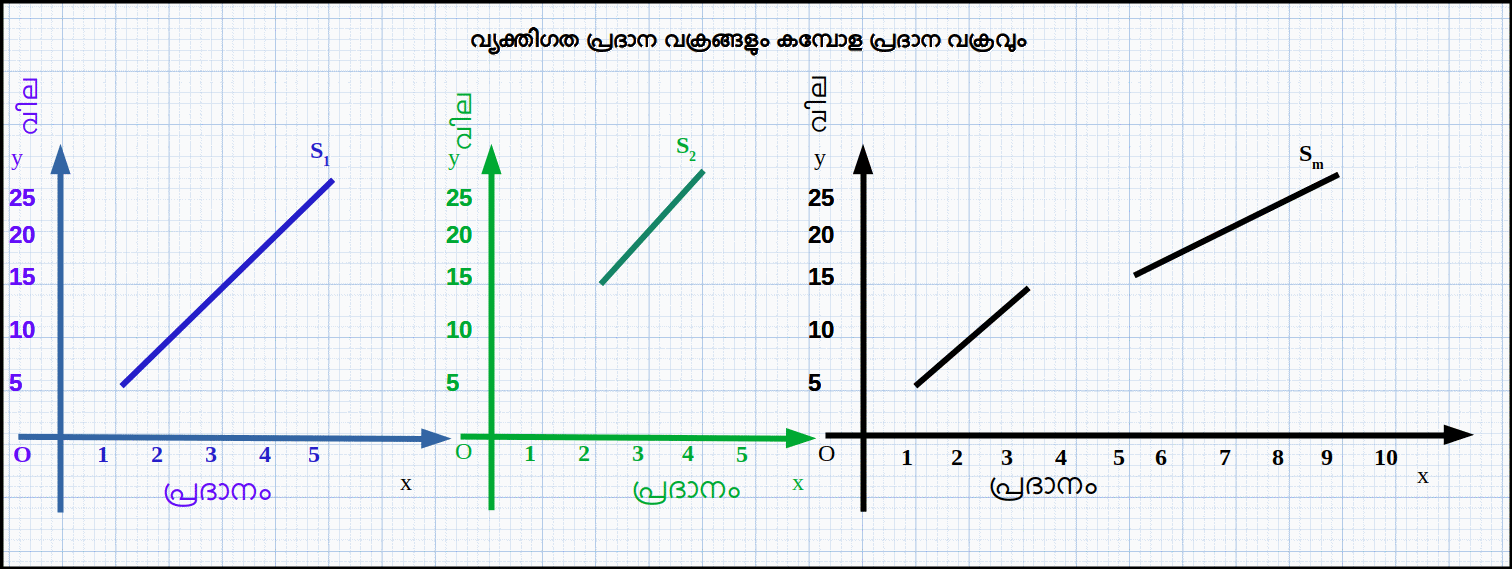
രണ്ട് ഉല്പാദക സ്ഥാപനങ്ങളുള്ള ഒരു വിപണിയിലെ കമ്പോള പ്രദാന വക്രം നമുക്ക് നിർമിക്കാം. സ്ഥാപനം 1 വില P1 ന് താഴെയാണെങ്കിൽ സാധനം ഉല്പാദിപ്പിക്കുകയില്ല. അതേസമയത്ത് സ്ഥാപനം 2 വില P2 ന് താഴെയാണെങ്കിൽ സാധനം ഉല്പാദിപ്പിക്കുകയില്ല. P2 > P1 ആണെന്ന് കരുതുക, ഗ്രാഫ് 4.21 ൽ ഭാഗം (a)ൽ സ്ഥാപനം 1 ന്റെ പ്രദാന വക്രവും ഭാഗം (b)ൽ സ്ഥാപനം 2 ന്റെ പ്രദാന വക്രവും ഭാഗം (c)ൽ കമ്പോള പ്രദാന വക്രവും കൊടുത്തിരിക്കുന്നു.
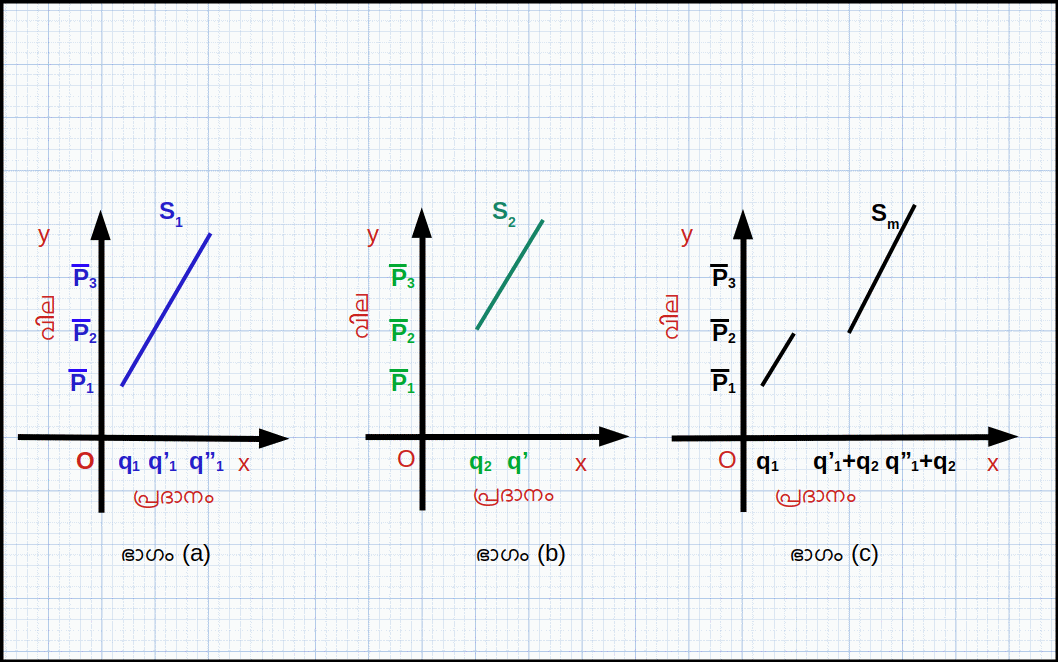
ഇവിടെ രണ്ട് സ്ഥാപനങ്ങൾ മാത്രമുള്ളതുകൊണ്ട് ഈ രണ്ട് സ്ഥാപനങ്ങളുടെ പ്രദാന വക്രങ്ങൾ കൂട്ടി കമ്പോള പ്രദാന വക്രം നിർമിച്ചിരിക്കുന്നു. അതു കൊണ്ട് ഒരു കമ്പോളത്തിലുള്ള എല്ലാ വ്യക്തിഗത പ്രദാന വക്രങ്ങളുടെയും തിരശ്ചീന തുകയാണ് കമ്പോള പ്രദാന വക്രം. സ്ഥാപനങ്ങളുടെ എണ്ണം വർധിക്കുമ്പോൾ കമ്പോള പ്രദാന വക്രം വലതുഭാഗത്തേക്ക് മാറുന്നു. Eg 4.14: പട്ടിക 4.8 അടിസ്ഥാനത്തിൽ വ്യക്തിഗത പ്രദാന വക്രവും കമ്പോള പ്രദാന വക്രവും ഗ്രാഫ് 4.22 ൽ കൊടുത്തിരിക്കുന്നു.
| Table 4.9 വ്യക്തിഗത പ്രദാനവും കമ്പോള പ്രദാനവും | |||
|---|---|---|---|
| വില (P) | സ്ഥാപനം 1 ന്റെ പ്രദാനം S1 | സ്ഥാപനം 2 ന്റെ പ്രദാനം S2 | കമ്പോള പ്രദാനം Sm |
| 5ൽ കുറവ് | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 |
| 10 | 2 | 0 | 2 |
| 15 | 3 | 2 | 5 |
| 20 | 4 | 3 | 7 |
| 25 | 5 | 4 | 9 |
പ്രദാനത്തിലെ മാറ്റങ്ങൾ അഥവാ വ്യതിയാനങ്ങൾ (Changes in Supply)
പ്രദാനത്തിൽ രണ്ടു തരത്തിലുള്ള മാറ്റങ്ങൾ ഉണ്ടാകുന്നു. അവ (1) പ്രദാന വക്രത്തിലൂടെയുള്ള മാറ്റങ്ങൾ (2) പ്രദാന വക്രത്തിന്റെ മാറ്റം ചാട്ടം.
പ്രദാന വക്രത്തിലൂടെയുള്ള മാറ്റങ്ങൾ (Movement along the supply curve)
വിലയിലുണ്ടാകുന്ന മാറ്റം മൂലം പ്രദാനത്തിലുണ്ടാകുന്ന മാറ്റത്തെയാണ് പ്രദാന വക്രത്തിലൂടെയുള്ള മാറ്റങ്ങൾ എന്നു പറയുന്നത്. ഇത് രണ്ടു തരത്തിലുണ്ട്. അവ (1) പ്രദാനത്തിന്റെ വികാസം (2) പ്രദാനത്തിന്റെ സങ്കോചം.
പ്രദാന വക്രത്തിലൂടെ മുകളിലേക്ക് മാറുന്നതിനെ പ്രദാനത്തിന്റെ വികാസം (Expansion) എന്നു പറയുന്നു. മറ്റൊരു വിധത്തിൽ പറഞ്ഞാൽ, വില വർധിക്കുമ്പോൾ പ്രദാനം വർധിക്കുന്നതിനെ പ്രദാനത്തിന്റെ വികാസം എന്നു പറയുന്നു. ഡയഗ്രം 4.23 ൽ വില P1 ൽനിന്ന് P2 വിലേക്ക് വർധിച്ചപ്പോൾ പ്രദാനം q1 ൽനിന്ന് q2 ആയി വർധിച്ചിരിക്കുന്നു. SS എന്ന പ്രദാന വകത്തിലെ a എന്ന ബിന്ദുവിൽ നിന്ന് മുകളിൽ b എന്ന ബിന്ദുവിലേക്കുള്ള മാറ്റത്തെ പ്രദാനത്തിന്റെ വികാസം എന്നു പറയുന്നു.
![]()

